【模型评估 06】超参数调优
对于很多算法工程师来说,超参数调优是一件非常头疼的事情。除了根据经验设定所谓的“合理值”之外,一般很难找到合理的方法去寻找超参数的最优取值。而与此同时,超参数对于模型效果的影响又至关重要。有没有一些可行的办法去进行超参数的调优呢?
超参数有哪些调优方法?
为了进行超参数调优,我们一般会采用网格搜索、随机搜索、贝叶斯优化等算法。在具体介绍算法之前,需要明确超参数搜索算法一般包括哪几个要素。
- 一是目标函数,即算法需要最大化/最小化的目标;
- 二是搜索范围,一般通过上限和下限来确定;
- 三是算法的其他参数,如搜索步长。
1. 网格搜索
网格搜索可能是最简单、应用最广泛的超参数搜索算法,他通过查找搜索范围内的所有点来确定最优值。如果采用较大的搜索范围以及较小的步长,网格搜索有很大概率找到全局最优值。然而,这种搜索方案十分消耗计算资源和时间,特别是需要调优的超参数比较多的时候。因此,在实际应用中,网格搜索一般会先使用较广的搜索范围和较大的步长,来寻找全局最优值可能的位置;然后会逐渐缩小搜索范围和步长,来寻找更精确的最优值。这种操作方案可以降低所需的时间和计算量,但由于目标函数一般是非凸的,所以很可能会错过全局最优值。
2. 随机搜索
随机搜索的思想与网格搜索比较相似,只是不再测试上界和下界之间的所有之,而是在搜索范围中随机选取样本点。它的理论依据是,如果样本点集足够大,那么通过随机采样也能大概率地找到全局最优值或其近似值。随机搜索一般会比网格搜索要快一些,但是和网格搜索的快速版一样。它的结果也是没法保证的。
3. 贝叶斯优化算法
贝叶斯优化算法在寻找最优最值参数时,采用了与网格搜索、随机搜索完全不同的方法。网格搜索和随机搜索在测试一个新点时,会忽略前一个点的信息;而贝叶斯优化算法则充分利用了之前的信息。贝叶斯优化算法通过对目标函数形状进行学习,找到使目标函数向全局最优值提升的参数。具体来说,它学习目标函数形状的方法是
- 首先根据先验分布,假设一个搜集函数;
- 然后,每一次使用新的采样点来测试目标函数时,利用这个信息来更新目标函数的先验分布。
- 最后,算法测试由后验分布给出的全局最值最可能出现的位置的点。
对于贝叶斯优化算法,有一个需要注意的地方,一旦找到了一个局部最优值,它会在该区域不断采样,所以很容易陷入局部最优值。为了弥补这个缺陷,贝叶斯优化算法会在探索和利用之间找到一个平衡点,“探索”就是在还未取样的区域获取采样点;而“利用”则是根据后验分布在最可能出现全局最值的区域进行采样。
代码实现
这些算法在Python中通常通过第三方库如scikit-learn、hyperopt和skopt等进行实现。以下是一些基本示例:
1. 网格搜索(Grid Search)使用scikit-learn:
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVCparam_grid = {'C': [0.1, 1, 10, 100, 1000], 'gamma': [1, 0.1, 0.01, 0.001, 0.0001],'kernel': ['rbf', 'poly', 'sigmoid']}grid = GridSearchCV(SVC(), param_grid, refit=True, verbose=2)
grid.fit(X_train, y_train)# 找到最佳参数
best_params = grid.best_params_2. 随机搜索(Randomized Search)使用scikit-learn:
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import uniformparam_dist = {'C': uniform(0.1, 1000),'gamma': uniform(0.0001, 1),'kernel': ['rbf', 'poly', 'sigmoid']}random_search = RandomizedSearchCV(SVC(), param_distributions=param_dist, n_iter=100, cv=5, verbose=2)
random_search.fit(X_train, y_train)# 找到最佳参数
best_params = random_search.best_params_3. 贝叶斯优化(Bayesian Optimization)使用hyperopt库:
from hyperopt import fmin, tpe, hp, STATUS_OKspace = {'C': hp.loguniform('C', -5, 5),'gamma': hp.loguniform('gamma', -8, 3),'kernel': hp.choice('kernel', ['rbf', 'poly', 'sigmoid'])
}def objective(params):model = SVC(**params)score = cross_val_score(model, X_train, y_train, cv=5).mean()return{'loss': -score, 'status': STATUS_OK}best = fmin(objective, space, algo=tpe.suggest, max_evals=100)# 最佳参数
best_params = dict(best)请注意,以上代码需要根据你的实际数据集X_train和y_train进行调整,并且假设你正在优化支持向量机(SVC)的参数。在贝叶斯优化中,你需要定义一个目标函数(objective function),这里我们用交叉验证得分作为目标。
相关文章:

【模型评估 06】超参数调优
对于很多算法工程师来说,超参数调优是一件非常头疼的事情。除了根据经验设定所谓的“合理值”之外,一般很难找到合理的方法去寻找超参数的最优取值。而与此同时,超参数对于模型效果的影响又至关重要。有没有一些可行的办法去进行超参数的调优…...

Matlab 字符识别OCR实验
Matlab 字符识别实验 图像来源于屏幕截图,要求黑底白字。数据来源是任意二进制文件,内容以16进制打印输出,0-9a-f’字符被16个可打印字符替代,这些替代字符经过挑选,使其相对容易被识别。 第一步进行线分割和字符分割…...

Docker Compose 部署 jenkins
Docker Compose 部署 jenkins jenkins 部署 Docker-Compose 部署 version: 3.1 services:jenkins:image: jenkinsci/blueoceanvolumes:- /data/jenkins/:/var/jenkins_home- /var/run/docker.sock:/var/run/docker.sock- /usr/bin/docker:/usr/bin/docker- /usr/lib/x86_64-…...

QT:使用QStyle实现QMenu的滚动效果
项目中,使用QMenu,多个QAction时 超出页面范围,需要菜单栏可以上下滚动。 实际QMenu是带滚动的,但是要知道怎么使用 还是需要查看QT源码,现在简单记录下我的使用方法。 QT源码中:q->style()->style…...

双指针问题——求只包含两个元素的最长连续子序列(子数组)
一,题目描述 你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果 种类 。 你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必…...
Unity组件开发--短连接HTTP
1.网络请求管理器 using LitJson; using Cysharp.Threading.Tasks; using System; using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEngine.Networking; using UnityEngine.Events;using System.Web; using System.Text; using Sy…...

真正的强大,原来是不动声色的
当一个人走过了绝境,他就会发现,真正的强大,原来是不动声色的。 他会停止一切自证,不再解释,话越来越少,眼神越来越坚定。 他不再模棱两可,唯唯诺诺,而是敢于断然拒绝,…...

git 查看tag和创建tag以及上传tag命令
文章目录 git 查看tag和创建tag以及上传tag命令git tagtag操作常用命令 git 查看tag和创建tag以及上传tag命令 git tag 如果你达到一个重要的阶段,并希望永远记住那个特别的提交快照,你可以使用 git tag 给它打上标签。 Git 的 tag 功能是一个非常有用…...
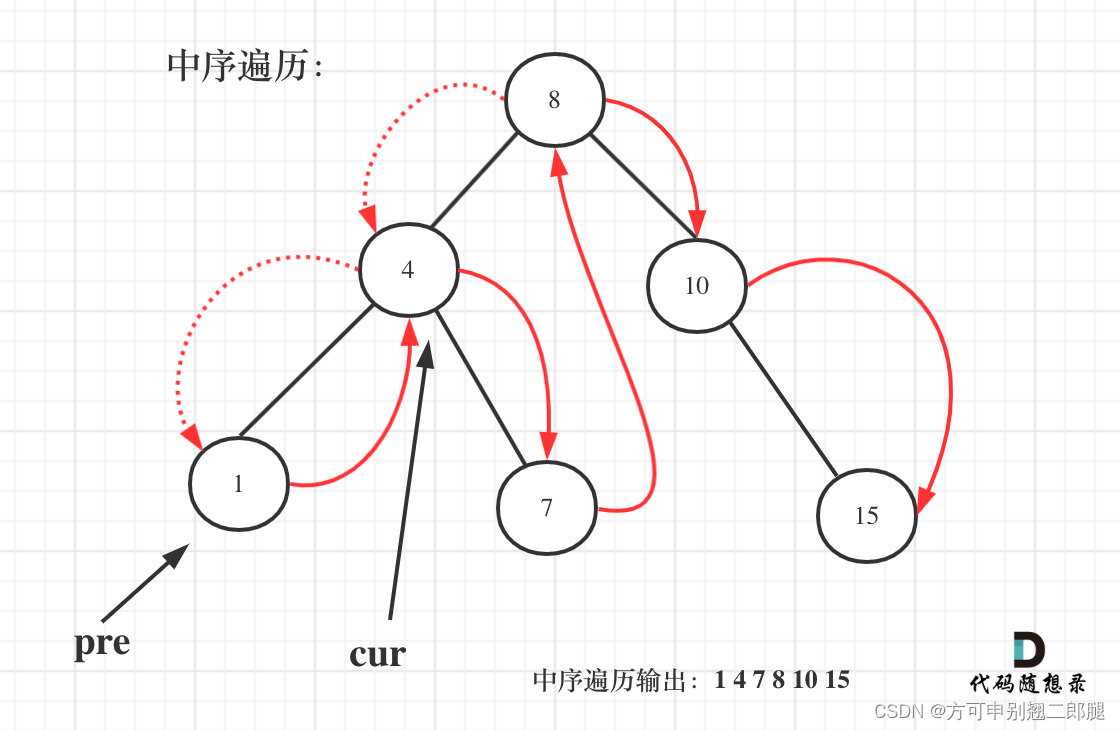
代码随想录二刷 |二叉树 | 二叉搜索树的最小绝对差
代码随想录二刷 |二叉树 | 二叉搜索树的最小绝对差 题目描述解题思路 & 代码实现递归法迭代法 题目描述 530.二叉搜索树的最小绝对差 给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。 示例&#…...

【Linux】Linux 系统编程——tree 命令
文章目录 1. 命令概述2. 命令格式3. 常用选项4. 相关描述4.1 tree 命令安装 5. 参考示例5.1 创建树形目录5.2 使用 tree 命令查看树形目录 1. 命令概述 tree 命令用于在命令行界面以树状图形式显示目录及其子目录的内容。这个命令递归地列出所有子目录,并可选择显示…...

Android简单控件
1.文本显示 设置文本内容的两种方式: 在XML文件中通过属性 android:text 设置文本 <resources><string name"app_name">chapter03</string><string name"hello">你好,世界</string> </resources&…...
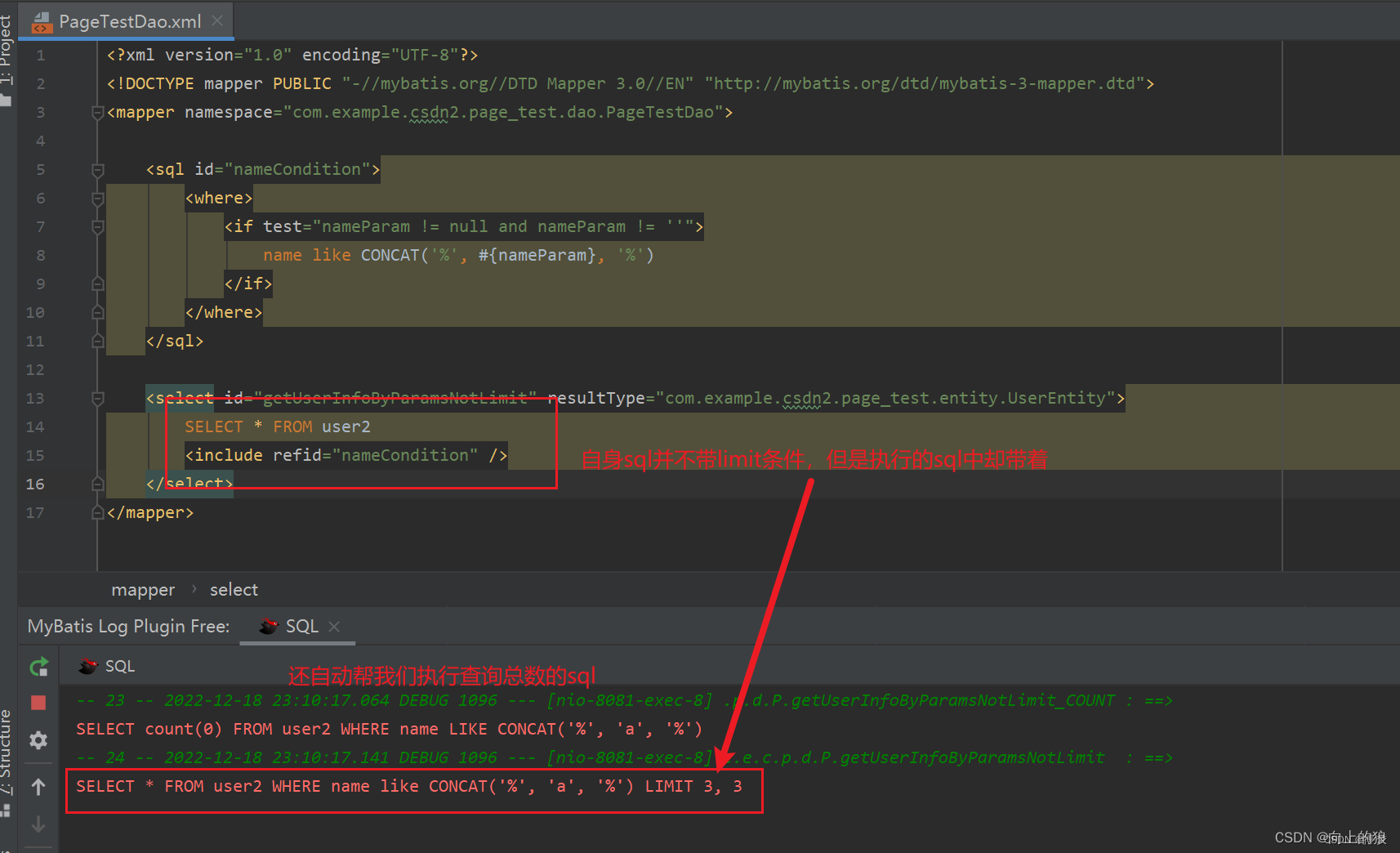
【Java 干货教程】Java实现分页的几种方式详解
一、前言 无论是自我学习中,还是在工作中,固然会遇到与前端搭配实现分页的功能,发现有几种方式,特此记录一下。 二、实现方式 2.1、分页功能直接交给前端实现 这种情况也是有的,(根据业务场景且仅仅只能用于数据量…...
关于Python里xlwings库对Excel表格的操作(三十一)
这篇小笔记主要记录如何【如何使用“Chart类”、“Api类"和“Axes函数”设置绘图区外框线型、颜色、粗细及填充颜色】。前面的小笔记已整理成目录,可点链接去目录寻找所需更方便。 【目录部分内容如下】【点击此处可进入目录】 (1)如何安…...

QML使用QCustomPlot笔记
这里在QML中使用QCustomPlot是定义一个继承自QQuickPaintedItem的类,它包含一个QCustomPlot对象,在paint函数中将这个对象转化为pixmap绘制到布局中显示。 在QML中使用QT的Widget控件也可以借鉴这个思路实现 顺便记录一下QCustomPlot的简单设置与使用。…...
【REST2SQL】06 GO 跨包接口重构代码
【REST2SQL】01RDB关系型数据库REST初设计 【REST2SQL】02 GO连接Oracle数据库 【REST2SQL】03 GO读取JSON文件 【REST2SQL】04 REST2SQL第一版Oracle版实现 【REST2SQL】05 GO 操作 达梦 数据库 对所有关系数据的操作都只有CRUD,采用Go 的接口interface{}重构代码…...
《NLP入门到精通》栏目导读
一、说明 栏目《NLP入门到精通》本着从简到难得台阶式学习过度。将自然语言处理得知识贯穿过来。本栏目得前导栏目是《深度学习》、《pytorch实践》,因此,读者需要一定得深度学习基础,才能过度到此栏目内容。 二、博客建设理念 本博客基地&am…...

C++学习笔记——类继承
目录 一、一个简单的基类 1.1封装性 1.2继承性 1.3虚函数 1.4多态性 二、基类 2.1一个简单的C基类的示例 2.2 Animal是一个基类。 三、继承 3.1概念 3.2is-a关系 3.3多态公有继承 3.4静态联编和动态联编 3.5访问控制 3.6ABC理念 一、一个简单的基类 C中的基类是一…...

ARCGIS PRO SDK 使用条件管理 Pro UI
ARCGIS PRO UI简单介绍以下: 第一步:在Config.daml中在</AddInfo>标签下加上条件<conditions>标签(必须添加的) <conditions><!-- 定义条件 ,此处定义了两个--Tab 另一个为 group><insert…...

Halcon经典的边缘检测算子Sobel/Laplace/Canny
Halcon经典的边缘检测算子 文章目录 Halcon经典的边缘检测算子1. Sobel算子2. Laplace 算子3. Canny 算子4. 总结 关于边缘检测,有许多经典的算子,各大图形处理库都有各自的边缘检测算子,这里简要介绍几种。 1. Sobel算子 Sobel算子结合了高…...

用单片机设计PLC电路图
自记: 见另一篇文章,MOS驱动差了一个充电电容,栅极电容充电会有问题; 光耦用的直插,但板子用的贴片,此文档仅供参考 基本列出了PCB板情况,基础元器件,部分连接,原理等…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
