四元数傅里叶变换(Quaternion Fourier Transforms) 在信号和图像处理中的应用
引言:
信号和图像处理是现代科学和工程领域中非常重要的一个方向,它涉及到对信号和图像进行分析、压缩、增强和恢复等操作。传统的信号和图像处理方法主要依赖于傅里叶变换和滤波器等工具,但这些方法在处理复杂系统时存在一定的局限性。近年来,四元数傅里叶变换作为一种新兴的数学工具,被广泛应用于信号和图像处理领域。本文将介绍四元数傅里叶变换的基本概念和原理,并探讨其在信号和图像处理中的应用。
一、四元数傅里叶变换的基本概念和原理
1.1 四元数傅里叶变换的定义
四元数傅里叶变换是一种将信号或图像从时域转换到频域的方法,它能够提取出信号或图像中的频率成分和相位信息。四元数傅里叶变换的定义为:
F(ω) = ∫f(t)e^(-iωt)dt
其中,F(ω)表示频率为ω的信号或图像的四元数傅里叶变换,f(t)表示原始信号或图像,e^(-iωt)表示复指数函数,t表示时间。
1.2 四元数傅里叶变换的性质
四元数傅里叶变换具有以下性质:
(1)线性性:对于任意两个信号或图像f(t)和g(t),它们的四元数傅里叶变换满足F(ω) = F1(ω) + F2(ω),其中F1(ω)和F2(ω)分别表示f(t)和g(t)的四元数傅里叶变换。
(2)共轭对称性:对于任意信号或图像f(t),其四元数傅里叶变换F(ω)满足F*(-ω) = F(ω),其中F*(-ω)表示F(ω)的共轭。
(3)时移性:对于任意信号或图像f(t),其四元数傅里叶变换F(ω)满足F(ω - Δω) = e^(-iΔωt)F(ω),其中Δω表示频率偏移量。
二、四元数傅里叶变换在信号和图像处理中的应用
2.1 信号分析
信
相关文章:
 在信号和图像处理中的应用)
四元数傅里叶变换(Quaternion Fourier Transforms) 在信号和图像处理中的应用
引言: 信号和图像处理是现代科学和工程领域中非常重要的一个方向,它涉及到对信号和图像进行分析、压缩、增强和恢复等操作。传统的信号和图像处理方法主要依赖于傅里叶变换和滤波器等工具,但这些方法在处理复杂系统时存在一定的局限性。近年来,四元数傅里叶变换作为一种新兴…...
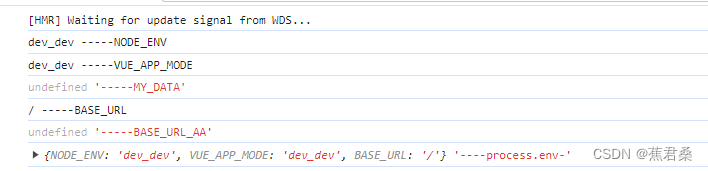
vue项目之.env文件.env.dev、test、pro
.env文件是vue运行项目时的环境配置文件。 .env: 全局默认配置文件,所有环境(开发、测试、生产等)均会加载并合并该文件 .env.development(开发环境默认命名) 开发环境的配置,文件名默认为.env.development,如果需要改名也是可以的…...

Fabric2.2:在有系统通道的情况下搭建应用通道
写在最前 在使用Fabric-SDK-Go1.0.0操作Fabric网络时遇到了bug。Fabric-SDK-GO的当前版本没有办法在没有系统通道的情况下创建应用通道,而Fabric的最新几个版本允许在没有系统通道的情况下搭建应用通道。为了解决这个矛盾并使用Fabric-SDK-GO完成后续的项目开发&…...
)
测试人员必备基本功(2)
容易被忽视的bug 第二章 修改表单容易被忽视的bug 文章目录 容易被忽视的bug第二章 修改表单容易被忽视的bug 前言一、修改表单二、具体功能1.修改角色2.接口设计 三、测试设计1.测试点2.容易发现bug的测试点如下: 总结 前言 一个WEB系统的所有功能模块࿰…...
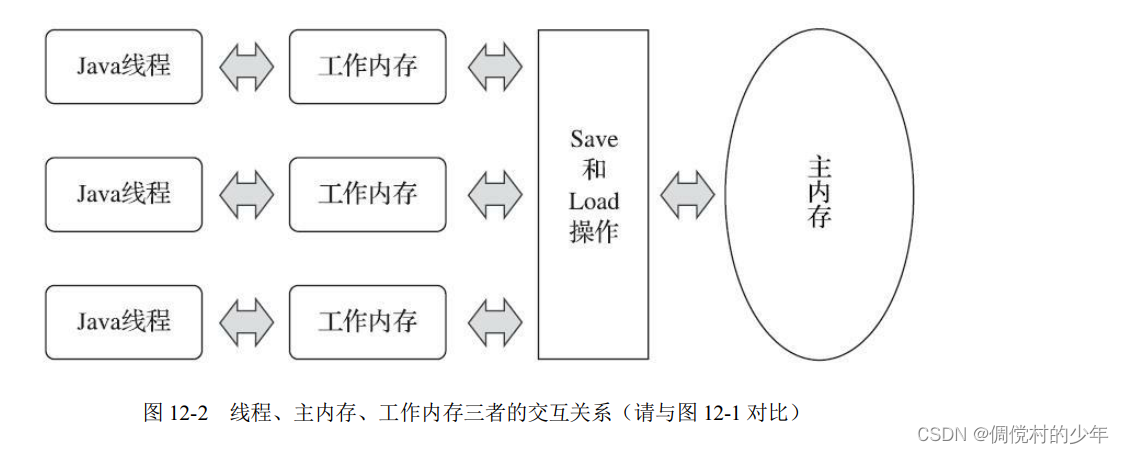
第十二章 Java内存模型与线程(一)
文章目录 12.3 Java内存模型12.3.1 主内存与工作内存12.3.2 内存间交互操作小结12.3.3 对于volatile型变量的特殊规则12.3.5 原子性、可见性与有序性12.3.6 先行发生原则 12.3 Java内存模型 12.3.1 主内存与工作内存 1.Java 内存模型规定了所有的变量都存储在主内存ÿ…...
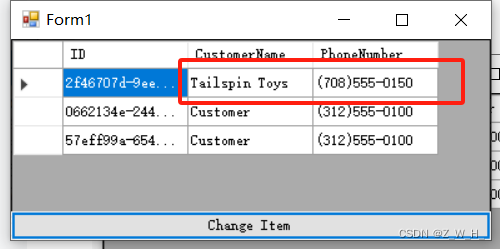
C# WPF 数据绑定
需求 后台变量发生改变,前端对应的相关属性值也发生改变 实现 接口 INotifyPropertyChanged 用于通知客户端(通常绑定客户端)属性值已更改。 示例 示例一 官方示例代码如下 using System; using System.Collections.Generic; using System.ComponentModel; using Sys…...

进程和线程的比较
目录 一、前言 二、Linux查看进程、线程 2.1 Linux最大进程数 2.2 Linux最大线程数 2.3 Linux下CPU利用率高的排查 三、线程的实现 四、上下文切换 五、总结 一、前言 进程是程序执行相关资源(CPU、内存、磁盘等)分配的最小单元,是一…...
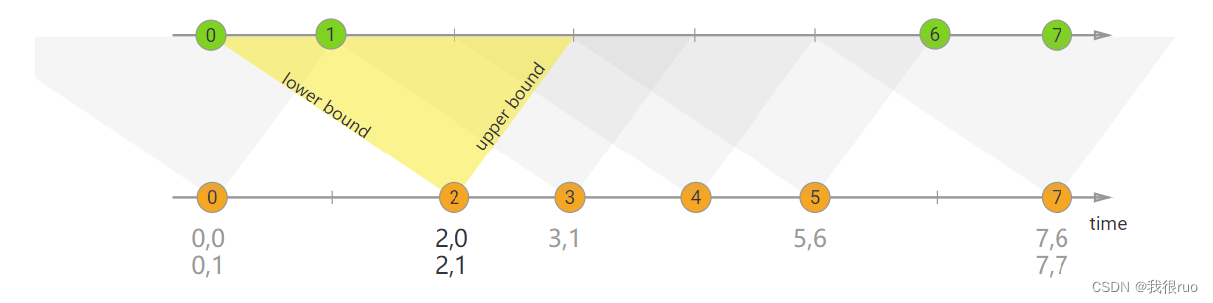
深入理解 Flink(四)Flink Time+WaterMark+Window 深入分析
Flink Window 常见需求背景 需求描述 每隔 5 秒,计算最近 10 秒单词出现的次数 —— 滑动窗口 每隔 5 秒,计算最近 5 秒单词出现的次数 —— 滚动窗口 关于 Flink time 种类 TimeCharacteristic ProcessingTimeIngestionTimeEventTime WindowAssign…...

科技创新领航 ,安川运动控制器为工业自动化赋能助力
迈入工业4.0时代,工业自动化的不断发展,让高精度运动控制成为制造业高质量发展的重要技术手段。北京北成新控伺服技术有限公司作为一家集工业自动化产品销售、系统设计、开发、服务于一体的高新技术企业,其引进推出的运动控制产品一直以卓越的…...

图像异或加密及唯密文攻击
异或加密 第一种加密方式为异或加密,异或加密的原理是利用异或的可逆性质,原始图像的像素八位bit分别与伪随机二进制序列异或,得到的图像就为加密图像。如下图对lena图像进行加密。 伪随机序列为一系列二进制代码,它受加密秘钥控…...

React Grid Layout基础使用
摘要 React Grid Layout是一个用于在React应用程序中创建可拖拽和可调整大小的网格布局的库。它提供了一个灵活的网格系统,可以帮助开发人员构建响应式的布局,并支持拖拽、调整大小和动画效果。本文将介绍如何使用React Grid Layout来创建自适应的布局。…...

第11章 1 文件及IO操作
文章目录 文件的概述及基本操作步骤 p151文件的写入操作 p152文件的读取操作及文件复制 p153文件的读取操作文件复制 with语句的使用 p154一维数据和二维数据的存储与读取 p155高维数据的存储和读取 p156os模块中的常用的函数 p157os.path模块中常用的函数 p158 文件的概述及基…...

Tomcat服务实例部署
目录 **Tomcat 由一系列的组件构成,其中核心的组件有三个:** 什么是 servlet? 什么是 JSP? Tomcat 功能组件结构: Container 结构分析: Tomcat 请求过程: ## Tomcat 服务部署 1.关闭防火墙…...
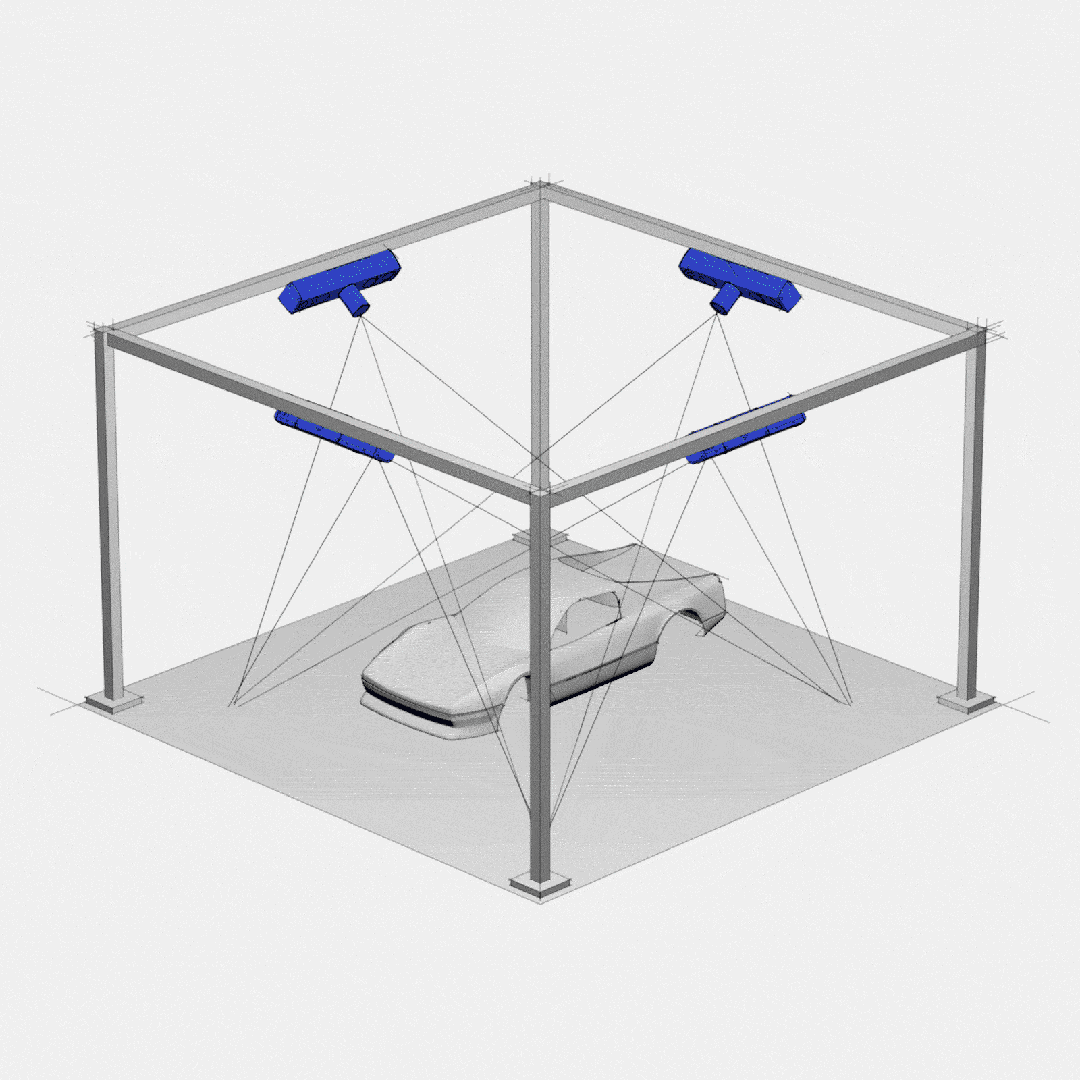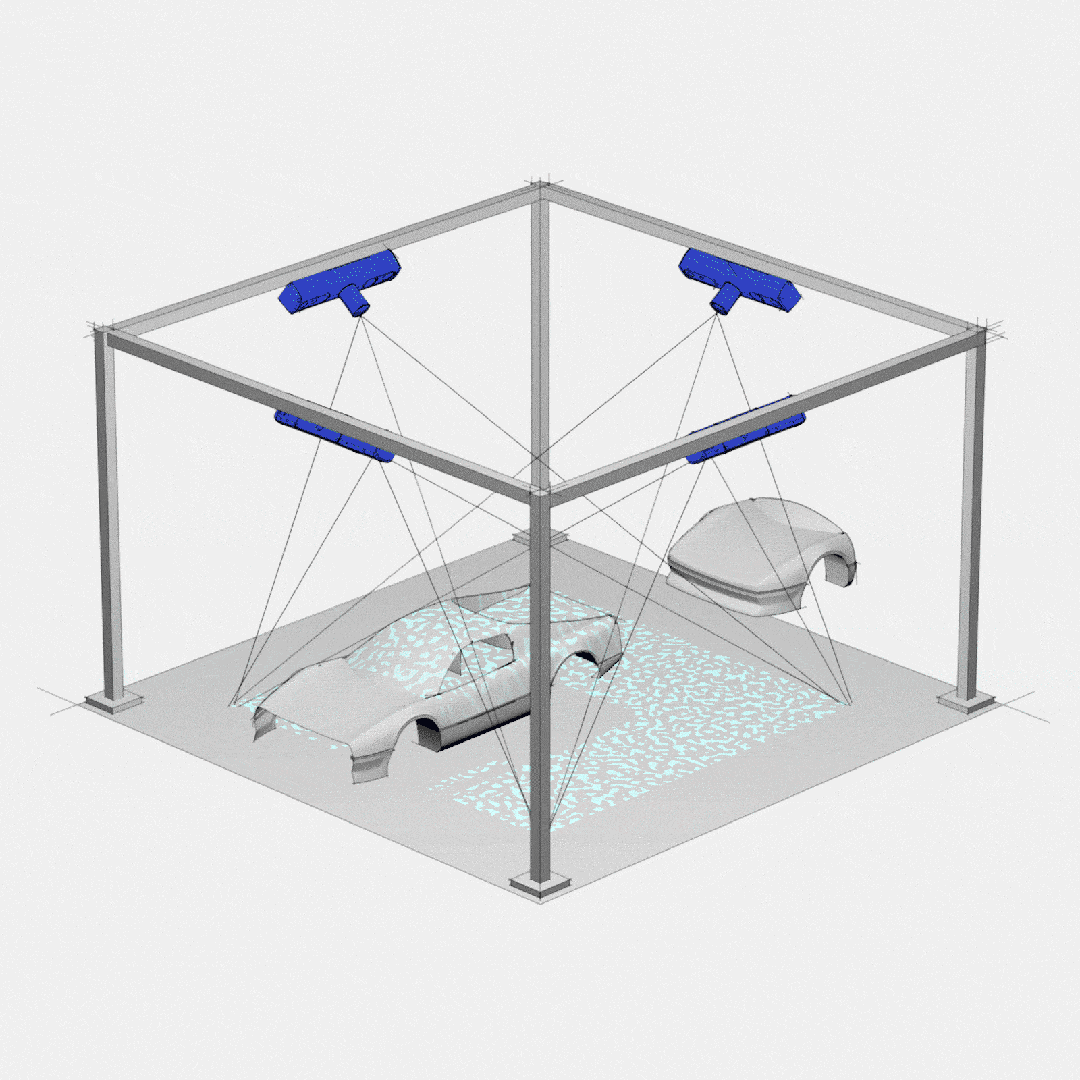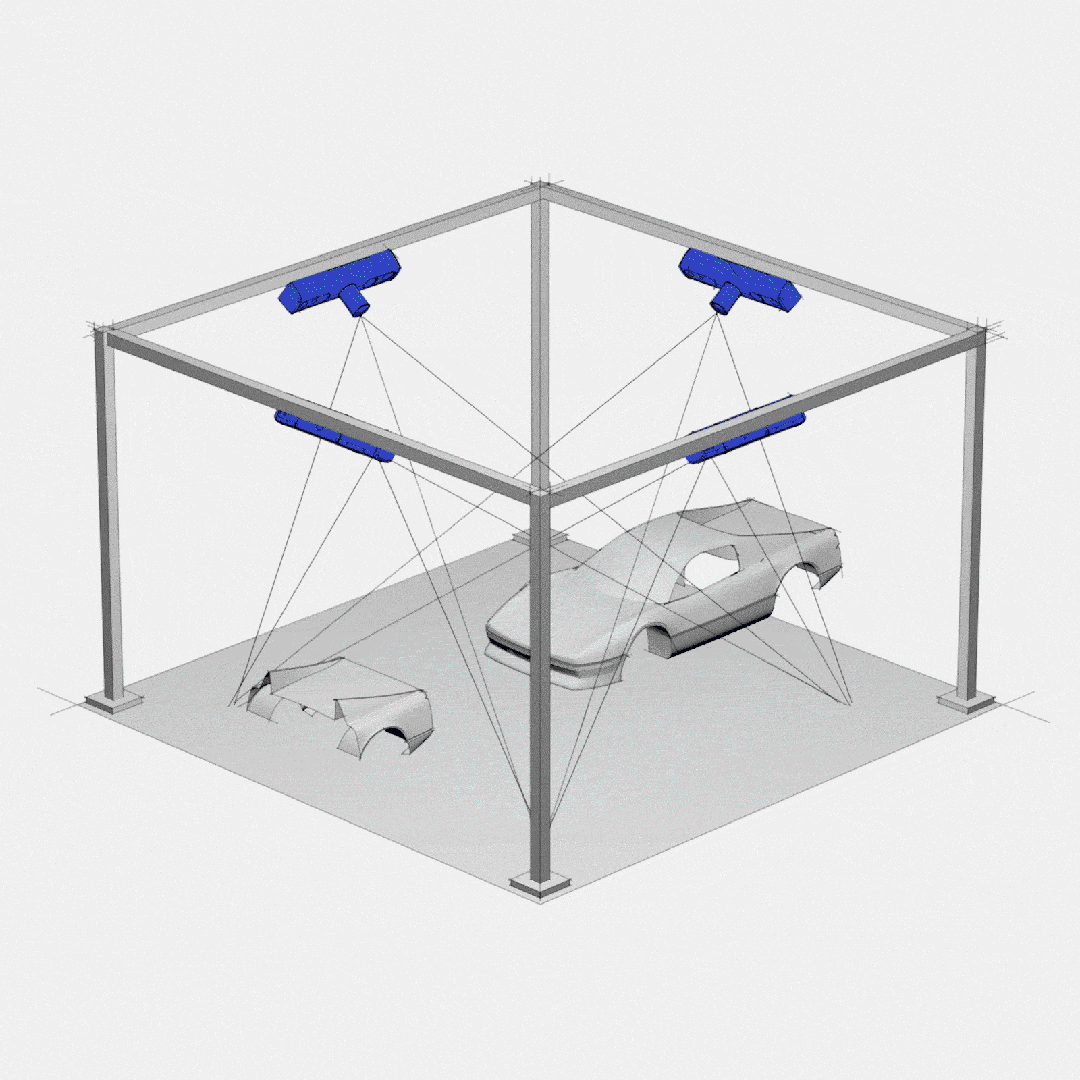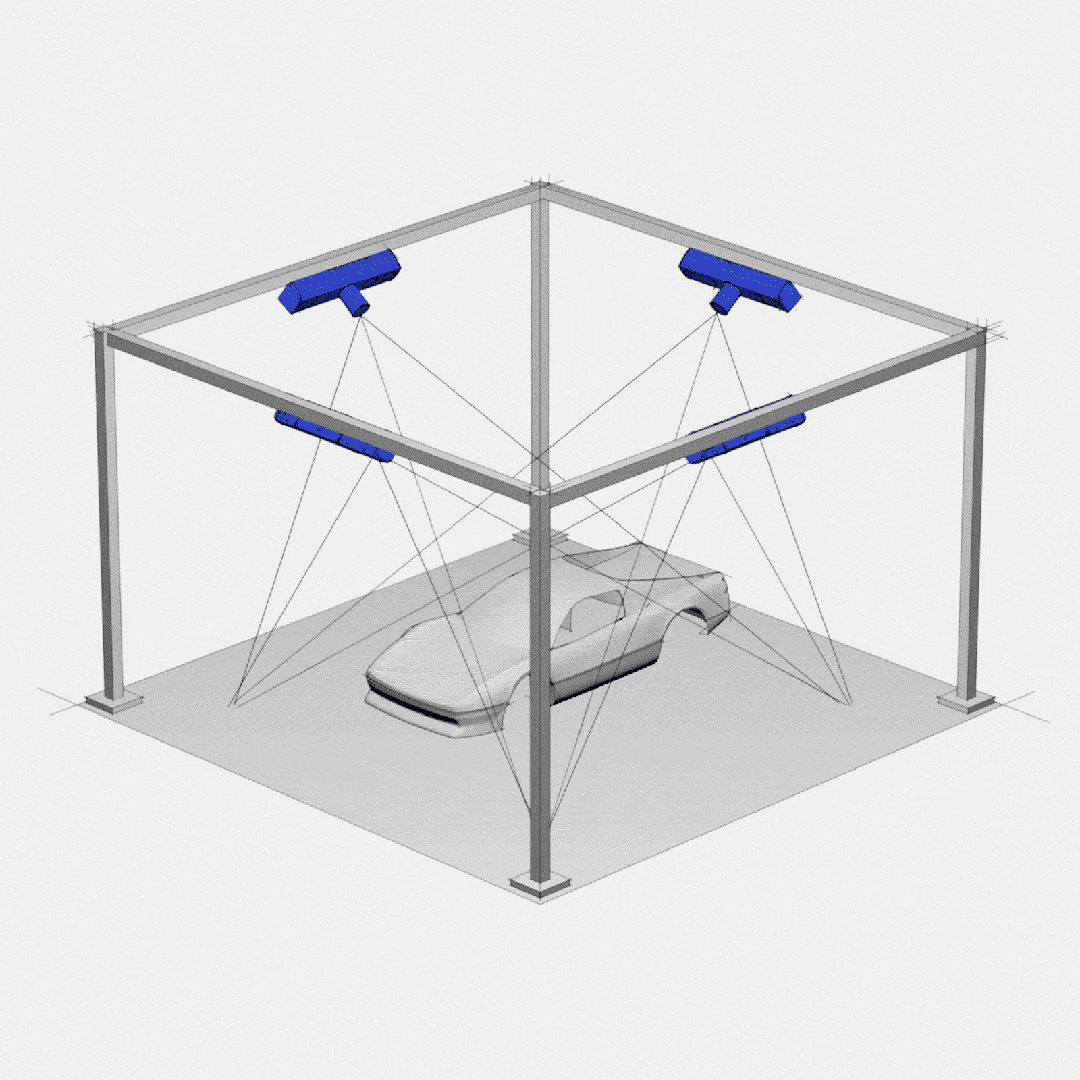
高精度彩色3D相机:开启崭新的彩色3D成像时代
3D成像的新时代 近年来,机器人技术的快速发展促使对3D相机技术的需求不断增加,原因在于,相机在提高机器人的性能和实现多种功能方面发挥了决定性作用。然而,其中许多应用所需的解决方案更复杂,仅提供环境的深度信息是…...
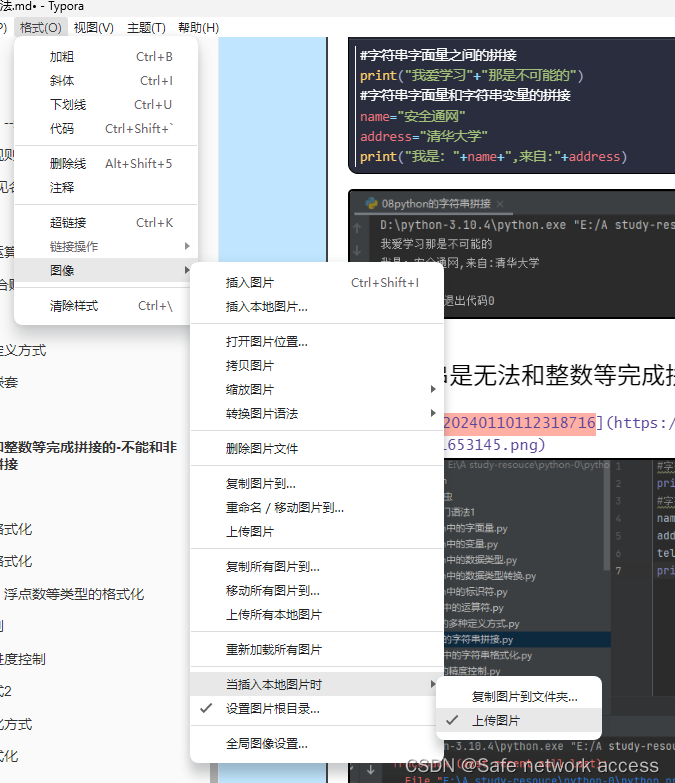
借助Gitee将typora图片上传CSDN
概述 前面已经发了一个如何借助Github将typora上的图片上传到csdn上,但这有个缺陷:需要科学上网才能加速查看已经上传到github上的图片,否则就会出现已经上传的图片,无法正常查看的问题 如何解决? 那就可以使用Gite…...

几件奇怪的事产生的疑团
1.记得当年在中国科技大学杨照华给我们上初等数论课(杨是北大毕业,闵嗣鹤教授的关门弟子,后来到华南师大任教),他说过“据华老(华罗庚)讲,希尔伯特最先解决华林问题的论文中用到二十…...
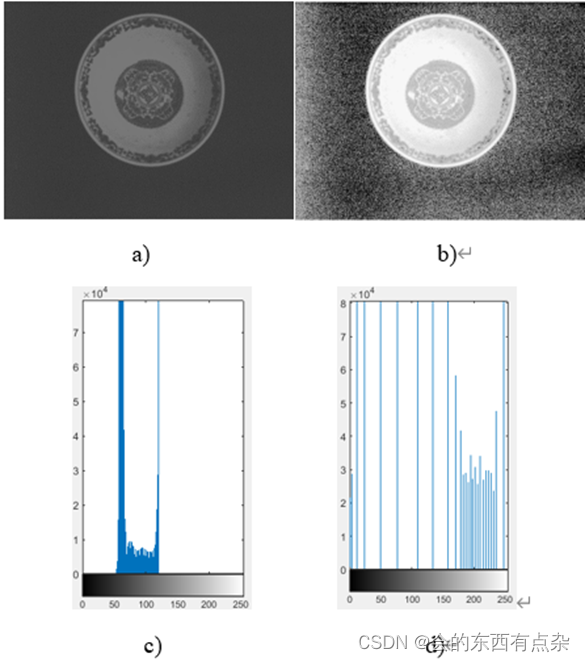
陶瓷碗口缺口检测-图像增强
图像增强 在采集图像的过程中,可能会有由于采集图像环境中光源照射不足,导致采集的图像对比度不足,图像视觉效果较暗的情况,可以通过直方图均衡化或者直方图规定化。如图a为原图像对比度低,图c为其直方图,…...
gitee创建远程仓库并克隆远程仓库到电脑
1、首先点加号新建一个仓库 2、输入仓库名,路径会自动填充,填写简单的仓库介绍,先选择私有,在仓库创建之后,可以改为开源 3、打开建好的仓库 4、复制仓库链接 5、打开一个文件夹(想要存储远程仓库的地址),在…...
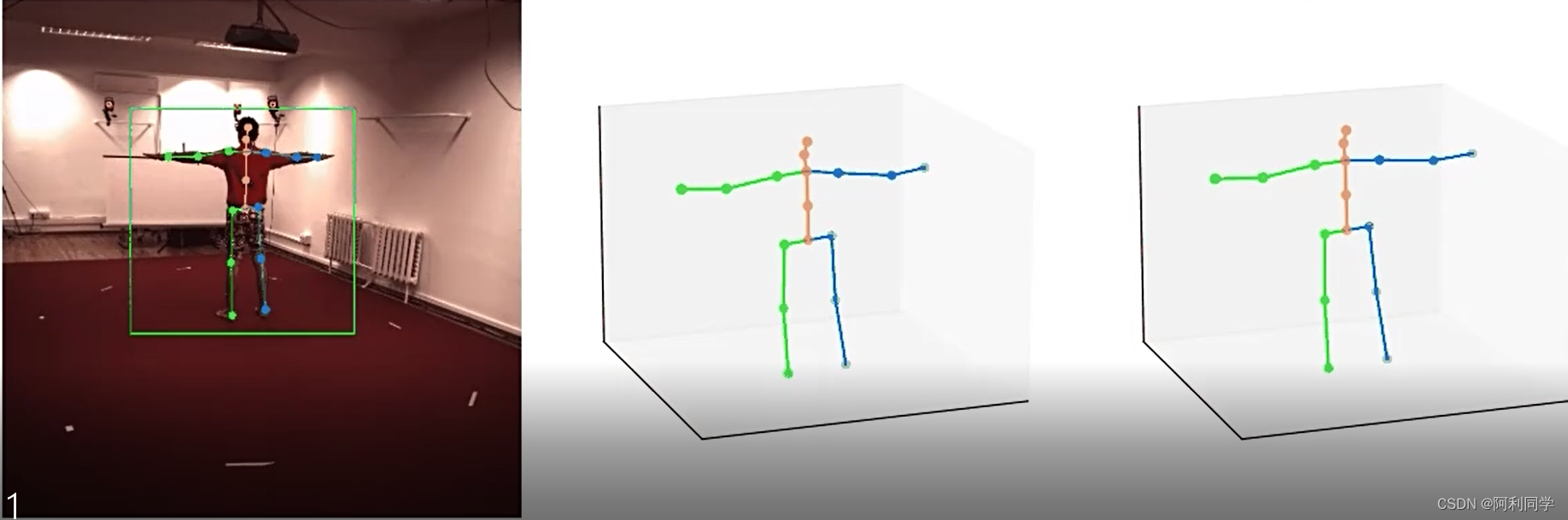
3D人体姿态估计(教程+代码)
3D人体姿态估计是指通过计算机视觉和深度学习技术,从图像或视频中推断出人体的三维姿态信息。它是计算机视觉领域的一个重要研究方向,具有广泛的应用潜力,如人机交互、运动分析、虚拟现实、增强现实等。 传统的2D人体姿态估计方法主要关注通…...
Python异步编程|PySimpleGUI界面读取PDF转换Excel
目录 实例要求 原始pdf文件格式 输出xls文件格式 运行界面 完整代码 代码分析 遍历表格 布局界面 控件简介 写入表格 表格排序 事件循环 异步编程 实例要求 使用PySimpleGUI做一个把单位考勤系统导出的pdf文件合并输出Excel的应用,故事出自࿱…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...
