Java并查集设计以及路径压缩实现
Java全能学习+面试指南:https://javaxiaobear.cn
并查集是一种树型的数据结构 ,并查集可以高效地进行如下操作:
- 查询元素p和元素q是否属于同一组
- 合并元素p和元素q所在的组
1、并查集的结构
并查集也是一种树型结构,但这棵树跟我们之前讲的二叉树、红黑树、B树等都不一样,这种树的要求比较简单:
- 每个元素都唯一的对应一个结点;
- 每一组数据中的多个元素都在同一颗树中;
- 一个组中的数据对应的树和另外一个组中的数据对应的树之间没有任何联系;
- 元素在树中并没有子父级关系的硬性要求;
2、并查集的API设计与实现
1、API设计
| 类名 | UnionFind |
|---|---|
| 构造方法 | UF(int N):初始化并查集,以整数标识(0,N-1)个结点 |
| 成员方法 | public int count():获取当前并查集中的数据有多少个分组 public boolean connected(int p,int q):判断并查集中元素p和元素q是否在同一分组中 public int find(int p):元素p所在分组的标识符 public void union(int p,int q):把p元素所在分组和q元素所在分组合并 |
| 成员变量 | private int[] eleAndGroup: 记录结点元素和该元素所在分组的标识 private int count:记录并查集中数据的分组个数 |
2、实现
1、UF(int N)构造方法实现
- 初始情况下,每个元素都在一个独立的分组中,所以,初始情况下,并查集中的数据默认分为N个组;
- 初始化数组eleAndGroup;
- 把eleAndGroup数组的索引看做是每个结点存储的元素,把eleAndGroup数组每个索引处的值看做是该结点所在的分组,那么初始化情况下,i索引处存储的值就是i
2、union(int p,int q)合并方法实现
- 如果p和q已经在同一个分组中,则无需合并
- 如果p和q不在同一个分组,则只需要将p元素所在组的所有的元素的组标识符修改为q元素所在组的标识符即可
- 分组数量-1
3、代码实现
public class UnionFind {/*** 记录结点元素和该元素所在分组的标识*/private int[] eleAndGroup;/*** 记录并查集中数据的分组个数*/private int count;public UnionFind(int n) {//初始情况下,每个元素都在一个独立的分组中,所以,初始情况下,并查集中的数据默认分为N个组this.count = n;//初始化数组eleAndGroup = new int[n];//把eleAndGroup数组的索引看做是每个结点存储的元素,// 把eleAndGroup数组每个索引处的值看做是该结点所在的分组,// 那么初始化情况下,i索引处存储的值就是ifor (int i = 0; i < n; i++) {eleAndGroup[i] = i;}}/*** 获取当前并查集中的数据有多少个分组* @return*/public int count(){return count;}/*** 判断并查集中元素p和元素q是否在同一分组中* @param p* @param q* @return*/public boolean connected(int p,int q){return eleAndGroup[p] == eleAndGroup[q];}/*** 元素p所在分组的标识符* @param p* @return*/public int find(int p){return eleAndGroup[p];}/*** 把p元素所在分组和q元素所在分组合并* @param p* @param q*/public void union(int p,int q){//如果q和p已经在同一个分组中,不需要合并if(connected(p, q)){return;}//不在一个分组中int pFind = find(p);int qFind = find(q);for (int i = 0; i < eleAndGroup.length; i++) {if (eleAndGroup[i] == pFind){eleAndGroup[i] = qFind;}}//数量减1count--;}
}
-
测试类
public class UnionFindTest {public static void main(String[] args) {UnionFind uf = new UnionFind(5);int count = uf.count();System.out.println("总共有"+count+"个分组");Scanner scanner = new Scanner(System.in);while (true){System.out.println("请输入你要合并的第一个点");int i = scanner.nextInt();System.out.println("请输入你要合并的第二个点");int j = scanner.nextInt();if(uf.connected(i,j)){System.out.println("结点"+ i +"和结点"+ j +"已经在同一个组");continue;}uf.union(i,j);System.out.println("总共还有"+uf.count()+"个分组");}} }
3、并查集应用举例
如果我们并查集存储的每一个整数表示的是一个大型计算机网络中的计算机,则我们就可以通过connected(intp,int q)来检测,该网络中的某两台计算机之间是否连通?如果连通,则他们之间可以通信,如果不连通,则不能通信,此时我们又可以调用union(int p,int q)使得p和q之间连通,这样两台计算机之间就可以通信了。
一般像计算机这样网络型的数据,我们要求网络中的每两个数据之间都是相连通的,也就是说,我们需要调用很多次union方法,使得网络中所有数据相连,其实我们很容易可以得出,如果要让网络中的数据都相连,则我们至少要调用N-1次union方法才可以,但由于我们的union方法中使用for循环遍历了所有的元素,所以很明显,我们之前实现的合并算法的时间复杂度是O(N^2),如果要解决大规模问题,它是不合适的,所以我们需要对算法进行优化。
4、算法优化
为了提升union算法的性能,我们需要重新设计find方法和union方法的实现,此时我们先需要对我们的之前数据结构中的eleAndGourp数组的含义进行重新设定:
- 我们仍然让eleAndGroup数组的索引作为某个结点的元素;
- eleAndGroup[i]的值不再是当前结点所在的分组标识,而是该结点的父结点;
1、API设计
| 类名 | UF_Tree |
|---|---|
| 构造方法 | UF_Tree(int N):初始化并查集,以整数标识(0,N-1)个结点 |
| 成员方法 | public int count():获取当前并查集中的数据有多少个分组 public boolean connected(int p,int q):判断并查集中元素p和元素q是否在同一分组中 public int find(int p):元素p所在分组的标识符 public void union(int p,int q):把p元素所在分组和q元素所在分组合并 |
| 成员变量 | private int[] eleAndGroup: 记录结点元素和该元素的父结点 private int count:记录并查集中数据的分组个数 |
2、实现
1、find(int p)查询方法实现
- 判断当前元素p的父结点eleAndGroup[p]是不是自己,如果是自己则证明已经是根结点了;
- 如果当前元素p的父结点不是自己,则让p=eleAndGroup[p],继续找父结点的父结点,直到找到根结点为止;
2、union(int p,int q)合并方法实现
- 找到p元素所在树的根结点
- 找到q元素所在树的根结点
- 如果p和q已经在同一个树中,则无需合并;
- 如果p和q不在同一个分组,则只需要将p元素所在树根结点的父结点设置为q元素的根结点即可;
- 分组数量-1
3、完成代码
public class UF_Tree {/*** 记录结点元素和该元素所在分组的标识*/private int[] eleAndGroup;/*** 记录并查集中数据的分组个数*/private int count;public UF_Tree(int n) {//初始情况下,每个元素都在一个独立的分组中,所以,初始情况下,并查集中的数据默认分为N个组this.count = n;//初始化数组eleAndGroup = new int[n];//把eleAndGroup数组的索引看做是每个结点存储的元素,// 把eleAndGroup数组每个索引处的值看做是该结点所在的分组,// 那么初始化情况下,i索引处存储的值就是ifor (int i = 0; i < n; i++) {eleAndGroup[i] = i;}}/*** 获取当前并查集中的数据有多少个分组* @return*/public int count(){return count;}/*** 判断并查集中元素p和元素q是否在同一分组中* @param p* @param q* @return*/public boolean connected(int p,int q){return eleAndGroup[p] == eleAndGroup[q];}/*** 元素p所在分组的标识符* @param p* @return*/public int find(int p){while (true){//判断当前元素p的父结点eleAndGroup[p]是不是自己,如果是自己则证明已经是根结点了;if(p == eleAndGroup[p]){return p;}//如果当前元素p的父结点不是自己,则让p=eleAndGroup[p],继续找父结点的父结点,直到找到根结点为止;p = eleAndGroup[p];}}/*** 把p元素所在分组和q元素所在分组合并* @param p* @param q*/public void union(int p,int q){//不在一个分组中int pFind = find(p);int qFind = find(q);if (qFind == pFind){return;}//如果p和q不在同一个分组,则只需要将p元素所在树根结点的父结点设置为q元素的根结点即可;eleAndGroup[pFind] = qFind;//数量减1count--;}
}
-
测试类
public class UnionFindTreeTest {public static void main(String[] args) {UF_Tree uf = new UF_Tree(5);int count = uf.count();System.out.println("总共有"+count+"个分组");Scanner scanner = new Scanner(System.in);while (true){System.out.println("请输入你要合并的第一个点");int i = scanner.nextInt();System.out.println("请输入你要合并的第二个点");int j = scanner.nextInt();if(uf.connected(i,j)){System.out.println("结点"+ i +"和结点"+ j +"已经在同一个组");continue;}uf.union(i,j);System.out.println("总共还有"+uf.count()+"个分组");}} }
5、路径压缩
UF_Tree中最坏情况下union算法的时间复杂度为O(N^2),其最主要的问题在于最坏情况下,树的深度和数组的大小一样,如果我们能够通过一些算法让合并时,生成的树的深度尽可能的小,就可以优化find方法。
之前我们在union算法中,合并树的时候将任意的一棵树连接到了另外一棵树,这种合并方法是比较暴力的,如果我们把并查集中每一棵树的大小记录下来,然后在每次合并树的时候,把较小的树连接到较大的树上,就可以减小树的深度。
只要我们保证每次合并,都能把小树合并到大树上,就能够压缩合并后新树的路径,这样就能提高find方法的效率。为了完成这个需求,我们需要另外一个数组来记录存储每个根结点对应的树中元素的个数,并且需要一些代码调整数组中的值。
1、API设计
| 类名 | UF_Tree_Weighted |
|---|---|
| 构造方法 | UF_Tree_Weighted(int N):初始化并查集,以整数标识(0,N-1)个结点 |
| 成员方法 | public int count():获取当前并查集中的数据有多少个分组 public boolean connected(int p,int q):判断并查集中元素p和元素q是否在同一分组中 public int find(int p):元素p所在分组的标识符 public void union(int p,int q):把p元素所在分组和q元素所在分组合并 |
| 成员变量 | private int[] eleAndGroup: 记录结点元素和该元素的父结点 private int[] sz: 存储每个根结点对应的树中元素的个数 private int count:记录并查集中数据的分组个数 |
2、实现
public class UFTreeWeighted {private int[] eleAndGroup;private int[] rootSize;private int count;public UFTreeWeighted(int count) {this.count = count;//初始化数组eleAndGroup = new int[count];rootSize = new int[count];/*** 把eleAndGroup数组的索引看做是每个结点存储的元素,* 把eleAndGroup数组每个索引处的值看做是该结点所在的分组,* 那么初始化情况下,i索引处存储的值就是i*/for (int i = 0; i < count; i++) {eleAndGroup[i] = i;}//把sz数组中所有的元素初始化为1,默认情况下,每个结点都是一个独立的树,每个树中只有一个元素for (int i = 0; i < count; i++) {rootSize[i] = 1;}}/*** 获取当前并查集中的数据有多少个分组* @return count*/public int count(){return count;}/*** 判断并查集中元素p和元素q是否在同一分组中* @param p* @param q* @return*/public boolean connected(int p,int q){return find(p) == find(q);}/*** 元素p所在分组的标识符* @param p* @return*/public int find(int p){while (true){if(p == eleAndGroup[p]){return p;}p = eleAndGroup[p];}}/*** :把p元素所在分组和q元素所在分组合并* @param p* @param q*/public void union(int p,int q){//找到p元素的根结点int pRoot = find(p);//找到q元素的根结点int qRoot = find(q);//如果已经在一个组中,无需合并if(pRoot == qRoot){return;}//不在一个组中,比较q所在树中的元素个数和p所在树中的元素个数,小树向大树合并if(rootSize[pRoot] < rootSize[qRoot]){eleAndGroup[pRoot] = qRoot;rootSize[qRoot] += rootSize[pRoot];}else {eleAndGroup[qRoot] = pRoot;rootSize[pRoot] += rootSize[qRoot];}//分组数组-1count--;}
}

相关文章:

Java并查集设计以及路径压缩实现
Java全能学习面试指南:https://javaxiaobear.cn 并查集是一种树型的数据结构 ,并查集可以高效地进行如下操作: 查询元素p和元素q是否属于同一组合并元素p和元素q所在的组 1、并查集的结构 并查集也是一种树型结构,但这棵树跟我们之…...
【leetcode】力扣算法之删除链表中倒数第n个节点【中等难度】
删除链表中倒数第n个节点 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 用例 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5] 输入:head [1], n 1 输出:[] 输入:head …...

C51--摇头测距小车
摇头测距小车——舵机和超声波封装 #include "reg52.h"#include "HC04.h" #include "Delay.h" #include "sg90.h" #include "motor.h"#define MIDDLE 0 #define LEFT 1 #define RIGHT 2void main() {char dir;double di…...

vue中slot和template用法传值
1 父页面调用assets-trend子组件,并接受assets-trend子组件传来的参数 <assets-trend style"flex: 2.7"><template slot-scope"slot">{{slot.slotMsg}}</template></assets-trend>2 子页面assets-trend使用slot传值 &…...
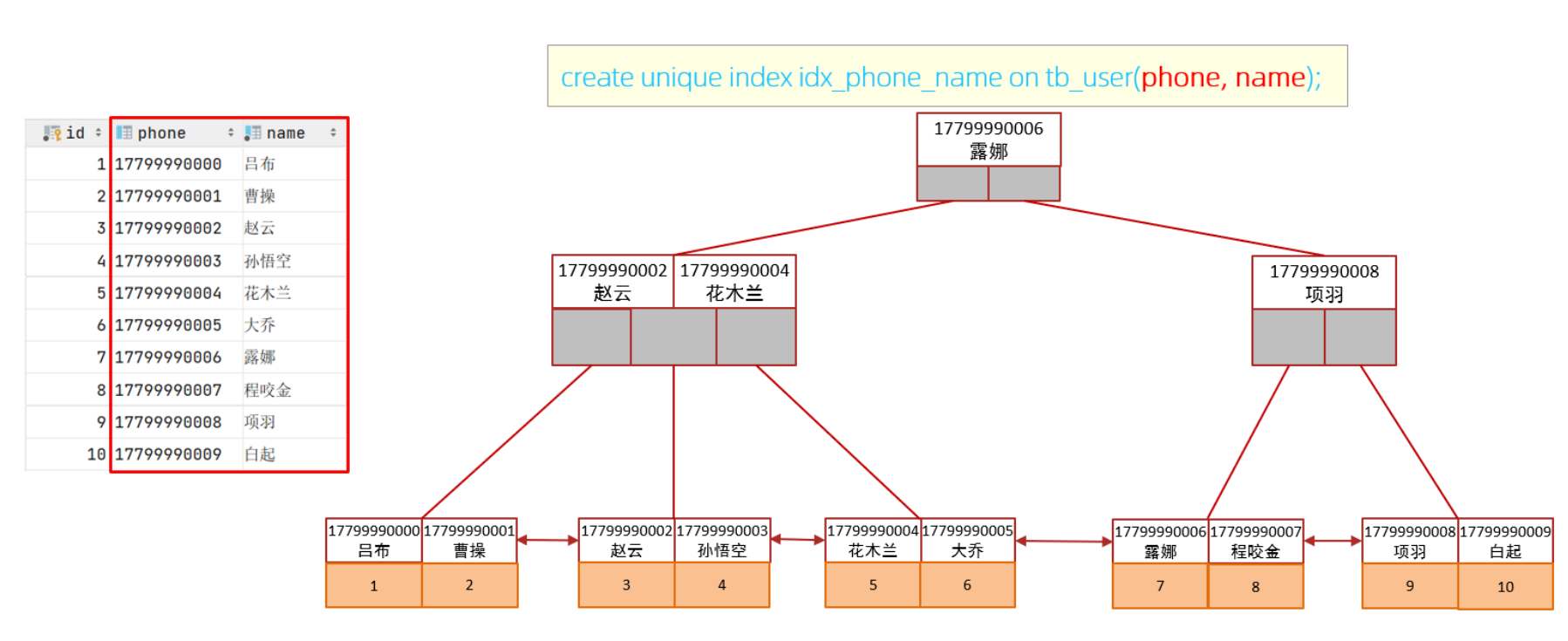
SQL性能分析-整理
昨日对MySQL的索引整理了一份小文档,对结构/分类/语法等做了一个小总结,具体文章可点击:MySQL-索引回顾,索引知识固然很重要,但引入运用到实际工作中更重要。 参考之前的文章:SQL优化总结以及参考百度/CSDN…...

常用计算电磁学算法特性与电磁软件分析
常用计算电磁学算法特性与电磁软件分析 参考网站: 计算电磁学三大数值算法FDTD、FEM、MOM ADS、HFSS、CST 优缺点和应用范围详细教程 ## 基于时域有限差分法的FDTD的计算电磁学算法(含Matlab代码)-框架介绍 参考书籍:The finite…...
PLC数组队列搜索FC(SCL代码+梯形图程序)
根据输入数据搜索输入数据队列中和输入数据相同的数,函数返回其所在队列的位置。这里我们需要用到博途PLC的数组指针功能,有关数组指针的详细使用方法,可以参考下面文章: 博途PLC数组指针: https://rxxw-control.blog.csdn.net/article/details/134761364 区间搜索FC …...

NUS CS1101S:SICP JavaScript 描述:前言、序言和致谢
前言 原文:Foreword 译者:飞龙 协议:CC BY-NC-SA 4.0 我有幸在我还是学生的时候见到了了不起的 Alan Perlis,并和他交谈了几次。他和我共同深爱和尊重两种非常不同的编程语言:Lisp 和 APL。跟随他的脚步是一项艰巨的任…...

软件测试常见问题2
1.用jmeter怎么进行测试? 使用JMeter进行测试的步骤如下: 启动JMeter,右键点击测试计划,选择添加->Threads(Users)->线程组,在线程组下创建请求。在请求中添加HTTP请求信息头,右键点击HTTP请求&…...
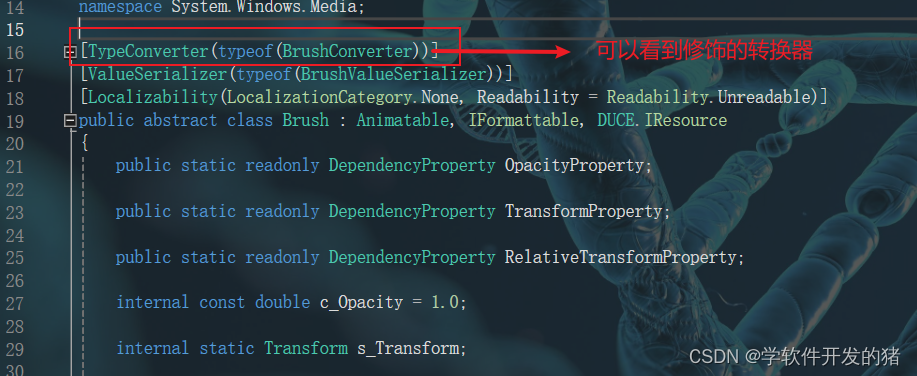
WPF XAML(一)
一、XAML的含义 问:XAML的含义是什么?为什么WPF中会使用XAML?而不是别的? 答:在XAML是基于XML的格式,XML的优点在于设计目标是具有逻辑性易读而且简单内容也没有被压缩。 其中需要提一下XAML文件在 Visu…...

每日一题:LeetCode-LCR 007. 三数之和
每日一题系列(day 18) 前言: 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🔎…...
 在信号和图像处理中的应用)
四元数傅里叶变换(Quaternion Fourier Transforms) 在信号和图像处理中的应用
引言: 信号和图像处理是现代科学和工程领域中非常重要的一个方向,它涉及到对信号和图像进行分析、压缩、增强和恢复等操作。传统的信号和图像处理方法主要依赖于傅里叶变换和滤波器等工具,但这些方法在处理复杂系统时存在一定的局限性。近年来,四元数傅里叶变换作为一种新兴…...
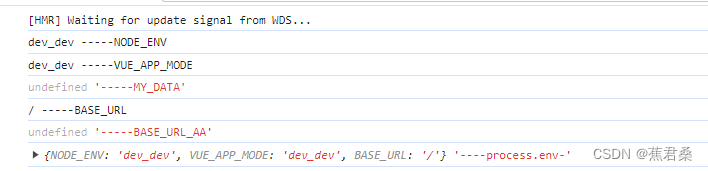
vue项目之.env文件.env.dev、test、pro
.env文件是vue运行项目时的环境配置文件。 .env: 全局默认配置文件,所有环境(开发、测试、生产等)均会加载并合并该文件 .env.development(开发环境默认命名) 开发环境的配置,文件名默认为.env.development,如果需要改名也是可以的…...

Fabric2.2:在有系统通道的情况下搭建应用通道
写在最前 在使用Fabric-SDK-Go1.0.0操作Fabric网络时遇到了bug。Fabric-SDK-GO的当前版本没有办法在没有系统通道的情况下创建应用通道,而Fabric的最新几个版本允许在没有系统通道的情况下搭建应用通道。为了解决这个矛盾并使用Fabric-SDK-GO完成后续的项目开发&…...
)
测试人员必备基本功(2)
容易被忽视的bug 第二章 修改表单容易被忽视的bug 文章目录 容易被忽视的bug第二章 修改表单容易被忽视的bug 前言一、修改表单二、具体功能1.修改角色2.接口设计 三、测试设计1.测试点2.容易发现bug的测试点如下: 总结 前言 一个WEB系统的所有功能模块࿰…...
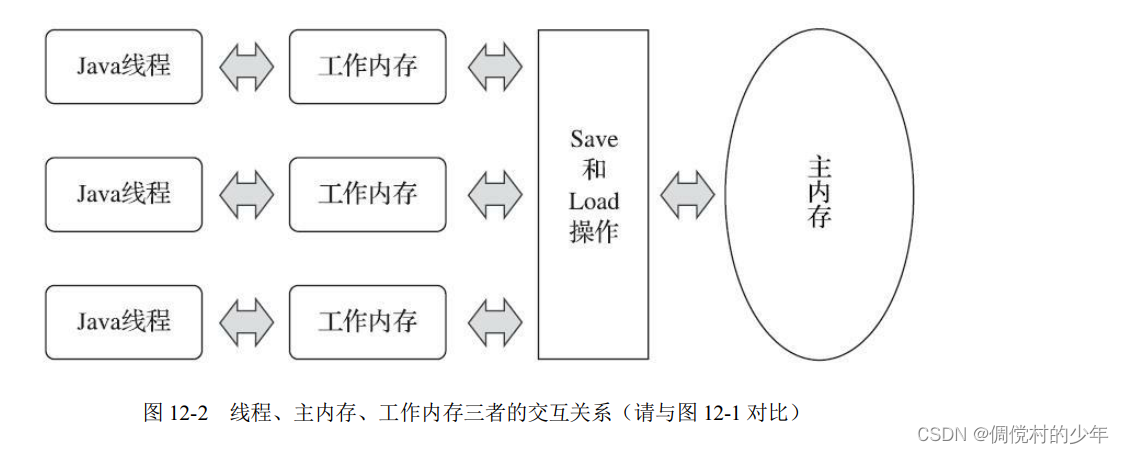
第十二章 Java内存模型与线程(一)
文章目录 12.3 Java内存模型12.3.1 主内存与工作内存12.3.2 内存间交互操作小结12.3.3 对于volatile型变量的特殊规则12.3.5 原子性、可见性与有序性12.3.6 先行发生原则 12.3 Java内存模型 12.3.1 主内存与工作内存 1.Java 内存模型规定了所有的变量都存储在主内存ÿ…...
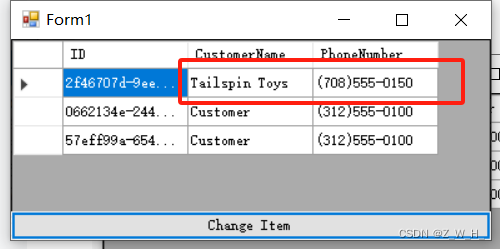
C# WPF 数据绑定
需求 后台变量发生改变,前端对应的相关属性值也发生改变 实现 接口 INotifyPropertyChanged 用于通知客户端(通常绑定客户端)属性值已更改。 示例 示例一 官方示例代码如下 using System; using System.Collections.Generic; using System.ComponentModel; using Sys…...

进程和线程的比较
目录 一、前言 二、Linux查看进程、线程 2.1 Linux最大进程数 2.2 Linux最大线程数 2.3 Linux下CPU利用率高的排查 三、线程的实现 四、上下文切换 五、总结 一、前言 进程是程序执行相关资源(CPU、内存、磁盘等)分配的最小单元,是一…...
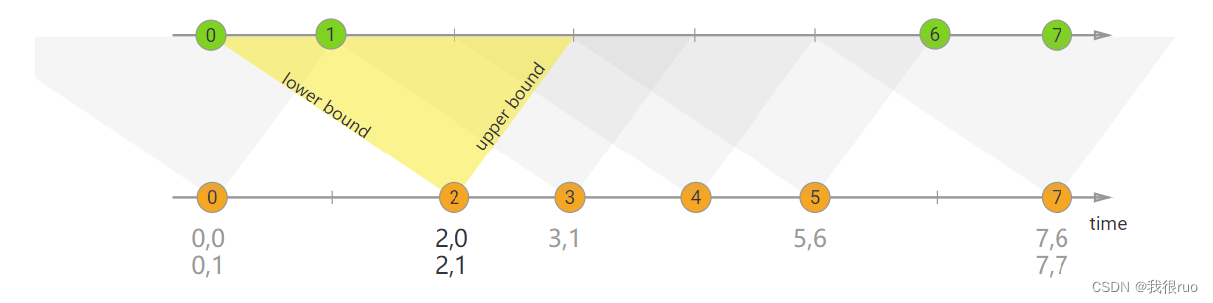
深入理解 Flink(四)Flink Time+WaterMark+Window 深入分析
Flink Window 常见需求背景 需求描述 每隔 5 秒,计算最近 10 秒单词出现的次数 —— 滑动窗口 每隔 5 秒,计算最近 5 秒单词出现的次数 —— 滚动窗口 关于 Flink time 种类 TimeCharacteristic ProcessingTimeIngestionTimeEventTime WindowAssign…...

科技创新领航 ,安川运动控制器为工业自动化赋能助力
迈入工业4.0时代,工业自动化的不断发展,让高精度运动控制成为制造业高质量发展的重要技术手段。北京北成新控伺服技术有限公司作为一家集工业自动化产品销售、系统设计、开发、服务于一体的高新技术企业,其引进推出的运动控制产品一直以卓越的…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
