vue中鼠标拖动触发滚动条的移动
前言
在做后端管理系统中,像弹窗或大的表单时,经常会有滚动条的出现,但有些时候如流程、图片等操作时,仅仅使用鼠标拖动滚动条操作不太方便,如果使用鼠标拖拽图片或容器来触发滚动条的移动就比较方便了
功能设计
如果要实现鼠标辅助触发滚动条的移动,需要借助 mousedown,mouseup,mousemove 三个事件,通过鼠标的移动来动态修改滚动条的scrollLeft和scrollTop,来模拟实现滚动条的位置变更。
考虑到鼠标的拖动有独立和可复用性,可以创建一个类来封装鼠标事件,使用时只要把事件挂到指定的容器上,就可以实现功能的复用
1、创建鼠标移动事件类
创建move.js
// 鼠标移动滚动位置类
class Drag {constructor(vm) {this.dragWrap = vm;// 要挂载的容器this._dom = {};this._x = 0;this._y = 0;this._top = 0;this._left = 0;this.move = false;this.down = false;this.init.apply(this, arguments);}// 绑定事件init() {this.bindEvent();}// 给要素增加鼠标事件// mousedown 按下初始化// mousemove 移动// mouseup,mouseleave 松开,移出结束移动bindEvent() {let t = this;this.dragWrap.addEventListener('mousedown', (e) => {e && e.preventDefault();if (!t.move) {t.move = false;t.down = true;t._x = e.clientX;t._y = e.clientY;t._top = t.dragWrap.scrollTop;t._left = t.dragWrap.scrollLeft;}});this.dragWrap.addEventListener('mouseup', (e) => {e && e.preventDefault();t.move = false;t.down = false;});this.dragWrap.addEventListener('mouseleave', (e) => {e && e.preventDefault();t.move = false;t.down = false;});this.dragWrap.addEventListener('mousemove', (e) => {if (t.down) {e && e.preventDefault();t.move = true;let x = t._x - e.clientX;let y = t._y - e.clientY;t.dragWrap.scrollLeft = t._left + x;t.dragWrap.scrollTop = t._top + y;}});}
}
export default Drag;
在页面中使用
1.在页面中使用move.js类,实现鼠标移动触发滚动条位置的移动
2.给svg添加放大功能
<template><el-row class="app-container"><el-col><el-form ref="form" v-model="value" label-width="80px" size="mini" style="position: absolute;top: 32px;z-index: 999;"><el-form-item label="缩放" prop="value"><el-input-number v-model="value" @change="changeSlider" :min="0" :max="3"></el-input-number></el-form-item></el-form><div id="navShow" style="text-align: center;overflow: hidden;height:90vh;border: 1px solid #000000;"><div><svg id="svgShow" style="cursor:pointer;width:96%;height:96%;padding: 10px;"></svg></div></div></el-col></el-row>
</template><script>
import Drag from '@/utils/move.js';
export default {name: 'ProcessingFlow',data() {return {value: 2,}},mounted() {this.changeSlider()this.initScroll()},methods: {changeSlider() {let svg = document.getElementById('svgShow')if (this.value === 1) {svg.style.transform = 'scale(1.6)'} else if (this.value === 2) {svg.style.transform = 'scale(1.9)'} else if (this.value === 3) {svg.style.transform = 'scale(2.2)'} else {svg.style.transform = 'scale(1)'}svg.style.transformOrigin = ' 0 0'let nav = document.getElementById('navShow')// 滚动元素的父容器:刷新滚轮nav.scrollIntoView()},initScroll() {let nav = document.getElementById('navShow')new Drag(nav)},}
}
</script><style scoped>
</style>
实现效果

相关文章:

vue中鼠标拖动触发滚动条的移动
前言 在做后端管理系统中,像弹窗或大的表单时,经常会有滚动条的出现,但有些时候如流程、图片等操作时,仅仅使用鼠标拖动滚动条操作不太方便,如果使用鼠标拖拽图片或容器来触发滚动条的移动就比较方便了 功能设计 如…...
1、理解Transformer:革新自然语言处理的模型
目录 一、论文题目 二、背景与动机 三、卖点与创新 四、解决的问题 五、具体实现细节 0. Transformer 架构的主要组件 1. 注意力、自注意力(Self-Attention)到多头注意力(Multi-Head Attention) 注意力到底是做什么的&…...
)
Acwing847 图中点的层次(bfs)
这道题用的是bfs,一开始用了dfs搜出了答案为4 题目 给定一个 n个点 m 条边的有向图,图中可能存在重边和自环。 所有边的长度都是 1,点的编号为 1∼n。 请你求出 1 号点到 n 号点的最短距离,如果从 1 号点无法走到 n 号点&…...
windows11通过虚拟机安装Ubuntu20.04
VMware 分为 VMware Workstation Pro 和 VMware Workstation Player, Pro体验期后收费,Player则免费。player 早期不能创建虚拟机,只能Pro创建好后给Player运行,而现在player早已加入创建虚拟机功能,所以使用体验上两者相差不大&a…...

时序预测 | Matlab实现EEMD-SSA-BiLSTM、EEMD-BiLSTM、SSA-BiLSTM、BiLSTM时序预测对比
时序预测 | Matlab实现EEMD-SSA-BiLSTM、EEMD-BiLSTM、SSA-BiLSTM、BiLSTM时间序列预测对比 目录 时序预测 | Matlab实现EEMD-SSA-BiLSTM、EEMD-BiLSTM、SSA-BiLSTM、BiLSTM时间序列预测对比预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现EEMD-SSA-BiLSTM、…...

Android14之解决Pixel手机联网出现感叹号(一百八十)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...
Vmware虚拟机问题解决方案 运行虚拟机系统蓝屏 运行虚拟机时报错VT-x
1. 运行虚拟机系统蓝屏 可能的原因有两个: 1). 虚拟机所在磁盘的空间不足 ; -------> 清理磁盘空间 。 2). 操作系统版本高, 需要适配新版本的Vmware ; ------> 卸载Vmware15版本, 安装Vmware16版本 。 2. 卸载Vmware步骤 1). 卸载已经安装的VMware 弹出确认框, 点击…...
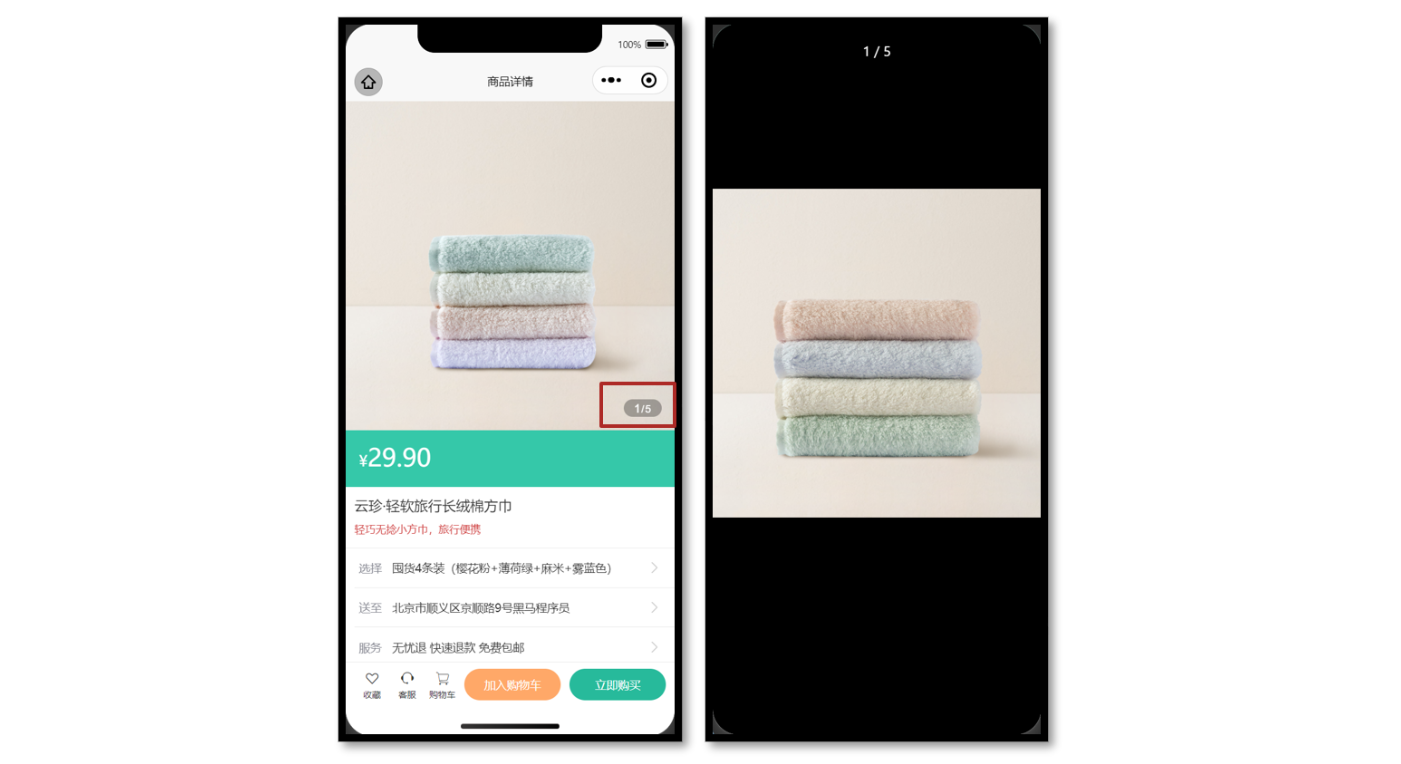
uni-app中轮播图实现大图预览
参考效果 当轮播图滑动切换的时候更新自定义下标,当图片被点击的时候大图预览。 参考代码 商品详情页轮播图交互 <script setup lang"ts"> // 轮播图变化时 const currentIndex ref(0) const onChange: UniHelper.SwiperOnChange (ev) > …...

了解什么是UV纹理?
在线工具推荐: 3D数字孪生场景编辑器 - GLTF/GLB材质纹理编辑器 - 3D模型在线转换 - Three.js AI自动纹理开发包 - YOLO 虚幻合成数据生成器 - 三维模型预览图生成器 - 3D模型语义搜索引擎 什么是UV? UV 是与几何图形的顶点信息相对应的二维纹理坐…...

【蓝桥备赛】wzy的数组Ⅱ——简单莫队问题
题目链接 wzy的数组Ⅱ 个人思路 本题需要统计区间范围内 数值为 x 在区间出现次数也为 x 的数的个数。区间询问 多次询问,我们选择 莫队。 将多次询问按照区间边界进行排序,每一次区间的移动,先去判断当前区间指针所指向的数是否符合题目…...
学习Qt笔记
前言: 学习笔记的内容来自B站up主阿西拜编程 《Qt6 C开发指南 》2023(上册,完整版)_哔哩哔哩_bilibili《Qt6 C开发指南 》2023(上册,完整版)共计84条视频,包括:00书籍介…...

pymssql 报错误解决办法:20002, severity 9
错误 解决办法 python3.6,安装pymssql低版本(pymssql-2.1.5-cp36-cp36m-win32.whl)...
Web缓存代理
目录 一.Web缓存代理 配置Nginx 缓存代理: 修改web服务器的配置文件: 修改192.168.233.10代理服务器的配置文件: 访问页面看看: 对于一些实时性要求非常高的页面或数据来说,就不应该去设置缓存,下面来…...

Rust-模式解构
match 首先,我们看看使用match的最简单的示例: exhaustive 有些时候我们不想把每种情况一一列出,可以用一个下划线来表达“除了列出来的那些之外的其他情况”: 下划线 下划线还能用在模式匹配的各种地方,用来表示…...
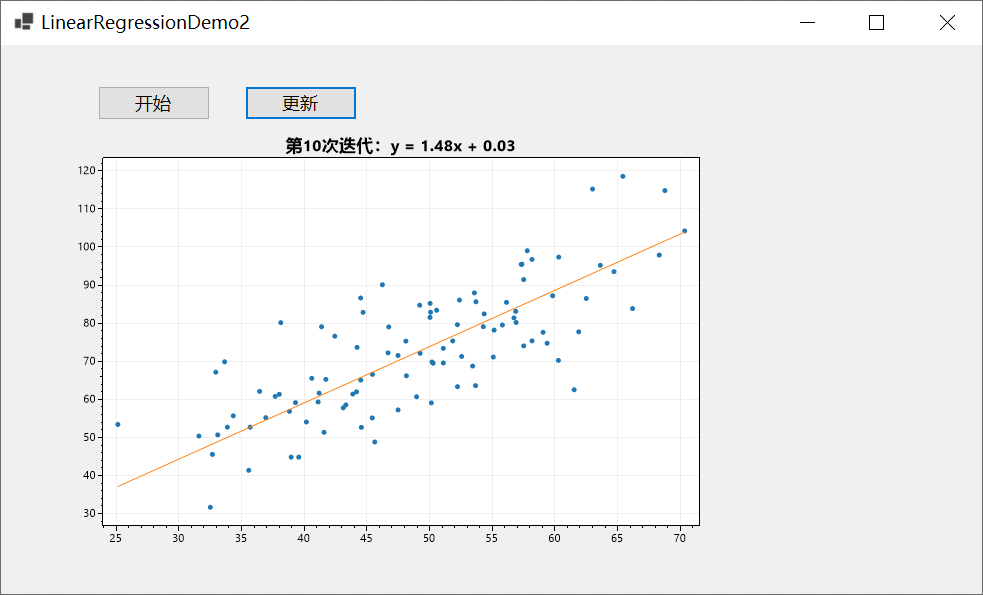
C#基于ScottPlot进行可视化
前言 上一篇文章跟大家分享了用NumSharp实现简单的线性回归,但是没有进行可视化,可能对拟合的过程没有直观的感受,因此今天跟大家介绍一下使用C#基于Scottplot进行可视化,当然Python的代码,我也会同步进行可视化。 P…...
基于JAVA+ssm开发的在线报名系统设计与实现【附源码】
基于JAVAssm开发的在线报名系统设计与实现【附源码】 🍅 作者主页 央顺技术团队 🍅 欢迎点赞 👍 收藏 ⭐留言 📝 🍅 文末获取源码联系方式 📝 🍅 查看下方微信号获取联系方式 承接各种定制系统 …...
)
蓝桥——第 3 场 小白入门赛(A-D)
文章目录 一、题目A.召唤神坤基本思路:代码 B.聪明的交换策略基本思路:代码 C.怪兽突击基本思路:代码 D.蓝桥快打基本思路代码 一、题目 A.召唤神坤 基本思路: 贪心, 使结果最大,希望两边w[i],w[k]是较大…...
Java项目:06 Springboot的进销存管理系统
作者主页:舒克日记 简介:Java领域优质创作者、Java项目、学习资料、技术互助 文中获取源码 进销存管理系统 介绍 进销存系统是为了对企业生产经营中进货、出货、批发销售、付款等全程进行(从接获订单合同开 始,进入物料采购、入…...
数据结构与算法之美学习笔记:47 | 向量空间:如何实现一个简单的音乐推荐系统?
这里写自定义目录标题 前言算法解析总结引申 前言 本节课程思维导图: 很多人都喜爱听歌,以前我们用 MP3 听歌,现在直接通过音乐 App 在线就能听歌。而且,各种音乐 App 的功能越来越强大,不仅可以自己选歌听࿰…...

5《Linux》
文章目录 查看端口号查看进程号查看IP查看与某台机器连接情况 Linux查看日志的命令?head [-n 行数参数】tail [-n 行数参数】cat [-n 行号展示】tac [-n 行号展示】 Linux操作文本-三剑客grep-擅长过滤正则过滤sed-擅长取行awk-擅长取列 Linux性能监控的命令&#x…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
