Leetcod面试经典150题刷题记录 —— 数学篇
| Leetcode面试经典150题刷题记录-系列 |
|---|
| Leetcod面试经典150题刷题记录——数组 / 字符串篇 |
| Leetcod面试经典150题刷题记录 —— 双指针篇 |
| Leetcod面试经典150题刷题记录 —— 矩阵篇 |
| Leetcod面试经典150题刷题记录 —— 滑动窗口篇 |
| Leetcod面试经典150题刷题记录 —— 哈希表篇 |
| Leetcod面试经典150题刷题记录 —— 区间篇 |
| Leetcod面试经典150题刷题记录——栈篇 |
| Leetcod面试经典150题刷题记录——链表篇 |
| Leetcod面试经典150题刷题记录——二叉树篇 |
| Leetcod面试经典150题刷题记录——二叉树层次遍历篇 |
| Leetcod面试经典150题刷题记录——二叉搜索树篇 |
Leetcod面试经典150题刷题记录 —— 数学篇
- 1. 回文数
- 解法1 字符串解法
- 解法2 官方解法
- 2. 加一
- 3. 阶乘后的零
- 解法1
- 解法2 考虑 [1,n] 中质因子 p 的个数。
- 4. x 的平方根 (扩展了解 快速平方根算法)
- 5. Pow(x,n)
- 6. 直线上最多的点数
1. 回文数
题目链接:回文数 - leetcode
题目描述:
给你一个整数x,如果x是一个回文整数,返回true;否则,返回false。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。例如,121是回文,而123不是。
题目归纳:
解题思路:
解法: 回文数 - leetcode官方题解
(1)转换成字符串进行求解。比较原始字符串与反转字符串。
(2)将数字的每一位存储至一个双向队列中,依次比较队头和栈顶元素:回文数 - Pensive Albattanicrq题解
(3)官方题解。上面两种方式都要完整遍历整个数字的位数,而官方题解只需要遍历到其中一半的位置,并且从空间使用效率上来说更高效。时间复杂度是 O ( l o g n ) O(logn) O(logn), n n n是数字的大小, l o g n logn logn是指数字总共有几位,这应该不难理解。
解法1 字符串解法
class Solution:def isPalindrome(self, x: int) -> bool:mylist = list(str(x))while len(mylist) > 1:if mylist.pop(0) != mylist.pop():return Falsereturn True
解法2 官方解法
class Solution:def isPalindrome(self, x: int) -> bool:# 可以直接判断的特殊情况# (1)负数。不是回文数# (2)数值末尾为0,则开头也为0,那么只有0符合条件。if x < 0 or (x%10 == 0 and x != 0):return FalserevertX = 0while x > revertX:revertX = 10 * revertX + x % 10x //= 10# 位数为偶数个 or 位数为奇数个return x == revertX or revertX//10 == x
2. 加一
题目链接:加一 - leetcode
题目描述:
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。你可以假设除了整数 0 之外,这个整数不会以零开头。
题目归纳:
解题思路:
解法: 加一 - leetcode官方题解
class Solution:def plusOne(self, digits: List[int]) -> List[int]:if len(digits) < 1: return [] # 空数组carry = 0 # 进位值digits = digits[::-1] # 翻转方便操作n = len(digits)p = 0while p < n:if p == 0: # 第1位数字要加1result = digits[0] + 1 + carrycarry = result // 10digits[0] = result % 10else:result = digits[p] + 0 + carrycarry = result // 10digits[p] = result % 10p += 1# 出来后若进位值carry仍大于0,数组需要append(carry)if carry > 0:digits.append(carry)return digits[::-1]
3. 阶乘后的零
题目链接:阶乘后的零 - leetcode
题目描述:
给定一个整数n,返回n!结果中尾随零的数量。提示n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1
题目归纳:
解题思路:
解法: 阶乘后的零 - leetcode官方题解
(1)因为 10 = 2 ∗ 5 10=2*5 10=2∗5,求末尾0的个数,即是求 m i n ( 质因子 5 的个数 , 质因子 2 的个数 ) min(质因子5的个数, 质因子2的个数) min(质因子5的个数,质因子2的个数)。
(2)再优化下,质因子 5 的个数不会大于质因子 2 的个数,
解法1
class Solution:def trailingZeroes(self, n: int) -> int:# 寻找阶乘的末尾有几个0# n! 尾0的个数即 n!中,因子10的个数,而10=2*5,因此转换成:求n!中质因子2的个数和质因子5的个数的较小值,即有多少个10参与了乘法,是由质因子2和5更小的那个数量来决定的# 质因子 5 的个数不会大于质因子 2 的个数# 而n!中质因子5的个数 = [1,n]的每个数的质因子5的个数之和,因此通过遍历[1,n]的所有5的倍数求出ans = 0for i in range(5, n+1, 5):while i%5 == 0: # (1)i要是5的倍数。i //= 5ans += 1 # (2)将i中质因子5的个数累加起来,比如25 = 5*5,两个质因数都为5return ans
解法2 考虑 [1,n] 中质因子 p 的个数。
class Solution:def trailingZeroes(self, n: int) -> int:# 仅考虑额外贡献的质因子个数 floor(n/p)# n 不变,p 越大,质因子个数越少,因此 [1,n] 中质因子 5 的个数不会大于质因子 2 的个数;ans = 0while n:n = n // 5ans += nreturn ans
4. x 的平方根 (扩展了解 快速平方根算法)
题目链接:x 的平方根 - leetcode
题目描述:
给你一个非负整数x,计算并返回x的 算术平方根 。由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。注意:不允许使用任何内置指数函数和算符,例如pow(x, 0.5)或者x ** 0.5。
题目归纳:
既然考察的是数学,那就请出牛顿提出的牛顿迭代法。这里可以拓展了解下 快速平方根倒数算法,还有那句著名的what the xxxx?。
解题思路:
解法: x 的平方根 - leetcode官方题解
class Solution:def mySqrt(self, x: int) -> int:# 牛顿迭代法if x == 0: return 0C, x0 = float(x), float(x)while True:xi = 0.5*(x0 + C/x0)if abs(x0 - xi) < 1e-7: # 两次求解的结果差距小于指定误差,可以返回return int(x0)x0 = xireturn int(x0)
| 参考文章或视频资料 |
|---|
| 【什么代码让程序员之神感叹“卧槽”?改变游戏行业的平方根倒数算法】- bilibili |
| 【没那么神秘的快速平方根倒数,给你解释一下这个数是怎么来的】- bilibili |
5. Pow(x,n)
题目链接:Pow(x,n) - leetcode
题目描述:
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。
题目归纳:
(1)常规思路。 x n = x ⋅ x ⋅ x ⋅ x . . . ⋅ x x^n = x · x · x · x \space\space ... \space\space· x xn=x⋅x⋅x⋅x ... ⋅x,这样方便理解,但计算并不快速。
(2)快速幂运算思路。其实快速幂运算就像微信小程序里的召唤神龙游戏,回忆下,召唤神龙是3只蝌蚪合成1只青蛙,3只青蛙合成1条鲤鱼 … … ,实际中你几乎不会真的拿9只蝌蚪来合成鲤鱼,而是遇到和自己一样大的动物就拉入自己的队伍,朝着更大型的动物合成迈进,这样的方式合并次数是最少的,直到 … … 召唤神龙。数学术语的描述具体可以看leetcode官方题解。
解题思路:
解法: Pow(x,n) - leetcode官方题解
class Solution:# 快速幂运算def quickMul(self, x: float, n: int) -> float:ans = 1.0while n > 0:if n & 1 == 1: # 末尾为1ans *= xx = x*x # x = x**2 反而会有问题n = n >> 1return ansdef myPow(self, x: float, n: int) -> float:if n >= 0:return self.quickMul(x, n)else:return 1.0 / self.quickMul(x, -n)
6. 直线上最多的点数
题目链接:直线上最多的点数 - leetcode
题目描述:
给你一个数组points,其中points[i] = [xi, yi]表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
题目归纳:
n n n个点,可以画出 n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1)条直线,如果再把每个点代入看是否符合该直线的方程,那时间复杂度将达到 O ( n 3 ) O(n^3) O(n3),这种算法绝对不可能被采用。
这里我插句题外话,这个算法只在平面上适用,比如说在《几何原本》中被奉为绝对真理的“两点确定一条直线”,在教科书上的表述并不是“两点只能确定一条直线”,因为在非欧几何中这个假设就不成立,若考虑地球是完美球体,那么地球的南极点到北极点有无数条经线,对于地球上的蚂蚁而言,这些经线毫无疑问就是其所处平面的直线,我们人类对宇宙的探索又何尝不是火鸡呢,谁知道两点之间有多少的连接可能性被空间本身的结构抛弃了。只做个人意见,如有错误请指正。
如果向量数据库采用的仍旧是占据主流的平面几何的学说,这是否符合大多数实际情况呢?会不会有些情况是需要用到非欧几何的呢?
解题思路:
解法: 直线上最多的点数 - leetcode官方题解
# 给一个数组points,其中,points[i] = [x_i, y_i]# 求,最多有多少个点在同一条直线上# 这道题对 向量数据库 应该非常重要,是向量数据库的基础算法,比如求向量之间的相似度与距离或者聚类# 可以考虑枚举所有point,假设直线经过该point时,该直线所能经过的最多的点数# 假设当前枚举到point{i},若直线同时经过另外两个不同的点j、k,那么(i,j)所在直线的斜率 = (i,k)所在直线的斜率# 于是,我们可以统计其它所有点与point{i}所连直线的斜率,出现次数最多的斜率,即为经过点数最多的斜率,其经过点数为 该斜率出现的次数+1(+1指point{i}自身)# 不采用浮点数记录斜率,因为精度可能不够,换用元组记录斜率的(分子,分母)的形式,这种记录形式可能有以下问题需要解决# (A) 两个元组:(1,2), (2,4)的斜率一致,所以还涉及到约分,即GCD最大公约数的求解# (B) 分子分母存在负数,(-1,2), (1,-2)的斜率一致,因此规定分母为非负整数,如果分母为负数,将二元组的两个数同时取反# (C) 直线为y=C或x=C时,传统的斜截式无法表达,采用特判法。# 再加以下4个小优化# (1)点的数量<=2,用一条直线将所有点串联,直接返回点的数量# (2)枚举到点i时,只考虑编号 >=i的点 与 点i之间的斜率,例如,编号小于点i的点j,当枚举到j自己的时候,就已经计算过点j与点i的斜率,即两点之间经过一条直线,不重复计算两次# (3)当找到的一条直线,已经经过了图中超过半数的点时,直接确定该直线为经过最多点的直线,然后继续按照该直线求点数# (4)当枚举到点i(编号从0开始)时,最多只能找到n-i个点共线,因为按优化(2),只考虑比自己编号大的。假设此前找到的共线的点数量最大值为k,如果有k>=n-i,此时即可停止枚举,因为不可能再找到更大的答案了。class Solution:def gcd(self, a, b): # 迭代法求最大公约数while b != 0:remain = a % b # 余数a = bb = remainreturn adef maxPoints(self, points: List[List[int]]) -> int:n = len(points)if n <= 2: # 优化(1)return nret = 0for i in range(n):if ret >= n-i or ret > (n/2): # 优化(4)与优化(3)breakmp = Counter()for j in range(i+1, n): # 优化(2),只考虑比自己编号大的点delta_x = points[i][0] - points[j][0] # △xdelta_y = points[i][1] - points[j][1] # △y# 对记录形式的优化(C)。特例判断if delta_x == 0:delta_y = 1elif delta_y == 0:delta_x = 1else:if delta_y < 0: # 对记录形式的优化(B)delta_x = -delta_xdelta_y = -delta_ygcdXY = self.gcd(abs(delta_x), abs(delta_y))delta_x = delta_x / gcdXYdelta_y = delta_y / gcdXYmp[str(delta_y + delta_x*20001)] += 1 # 看官方题解maxn = 0for k,v in mp.items():maxn = max(maxn, v+1)ret = max(ret, maxn)return ret
相关文章:

Leetcod面试经典150题刷题记录 —— 数学篇
Leetcode面试经典150题刷题记录-系列Leetcod面试经典150题刷题记录——数组 / 字符串篇Leetcod面试经典150题刷题记录 —— 双指针篇Leetcod面试经典150题刷题记录 —— 矩阵篇Leetcod面试经典150题刷题记录 —— 滑动窗口篇Leetcod面试经典150题刷题记录 —— 哈希表篇Leetcod…...

x-cmd pkg | csview - 美观且高性能的 csv 数据查看工具
目录 介绍首次用户功能特点类似工具与竞品进一步阅读 介绍 csview 是一个用于在命令行中查看 CSV 文件的工具,采用 Rust 语言编写的,支持中日韩/表情符号。它允许用户在终端中以表格形式查看 CSV 数据,可以对数据进行排序、过滤、搜索等操作…...
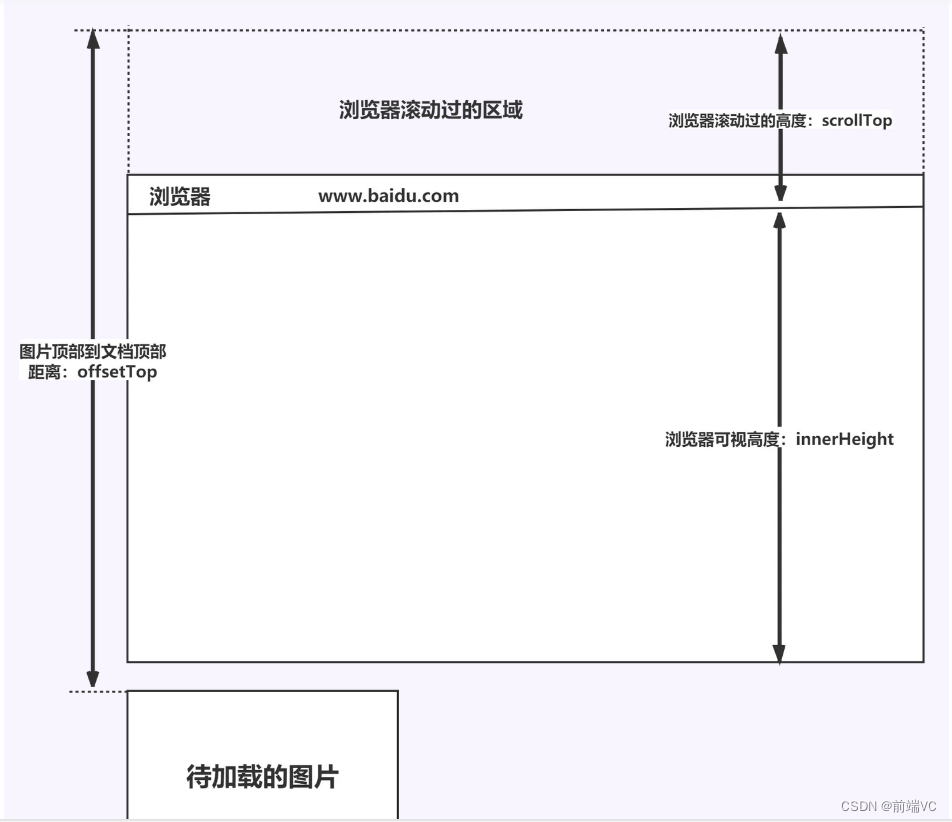
前端八股文(性能优化篇)
目录 1.CDN的概念 2.CDN的作用 3.CDN的原理 4.CDN的使用场景 5.懒加载的概念 6.懒加载的特点 7.懒加载的实现原理 8.懒加载与预加载的区别 9.回流与重绘的概念及触发条件 (1)回流 (2)重绘 10. 如何避免回流与重绘&#…...
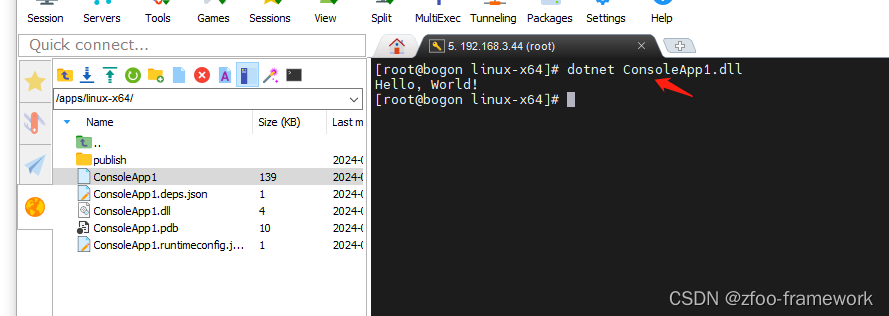
.Net Core项目在linux部署实战 1.sdk下载 2.环境变量配置/ect/profile 3.运行
1)下载.net core sdk https://download.visualstudio.microsoft.com/download/pr/01292c7c-a1ec-4957-90fc-3f6a2a1e5edc/025e84c4d9bd4aeb003d4f07b42e9159/dotnet-sdk-6.0.418-linux-x64.tar.gz 2)配置下环境变量 step1: // 解压到指定目录 mkdir -p $HOME/dotnet &…...

Python 基于Open3D的点云均匀下采样算法
目录 一、算法概述二、代码示例三、测试示例一、算法概述 点云均匀下采样算法:是在保持点云关键特征的前提下,减少点云数据的数量。 算法流程: 首先使用o3d.io.read_point_cloud函数读取点云数据。然后,使用uniform_down_sample函数进行均匀下采样,将点云数据按照指定的采…...

【MySQL】本地创建MySQL数据库详解
文章目录 下载MySQL安装重置密码本地连接 下载MySQL 下载网址:https://dev.mysql.com/downloads/mysql/ 安装 将下载好的压缩包解压到D盘。 在解压好的文件夹中创建my.ini文件。 将以下代码复制粘贴到创建好的my.ini文件中。注意修改文件路径。 [mysqld] #设置…...

18、golang时间管理
时间 时间是非常重要的,离开了时间,几乎没有哪个生产环境数据能够有意义。 在Go语言中,时间定义为Time结构体。 package mainimport ("fmt""time" )func main() {var t time.Now()fmt.Println(t) fmt.Printf("%…...
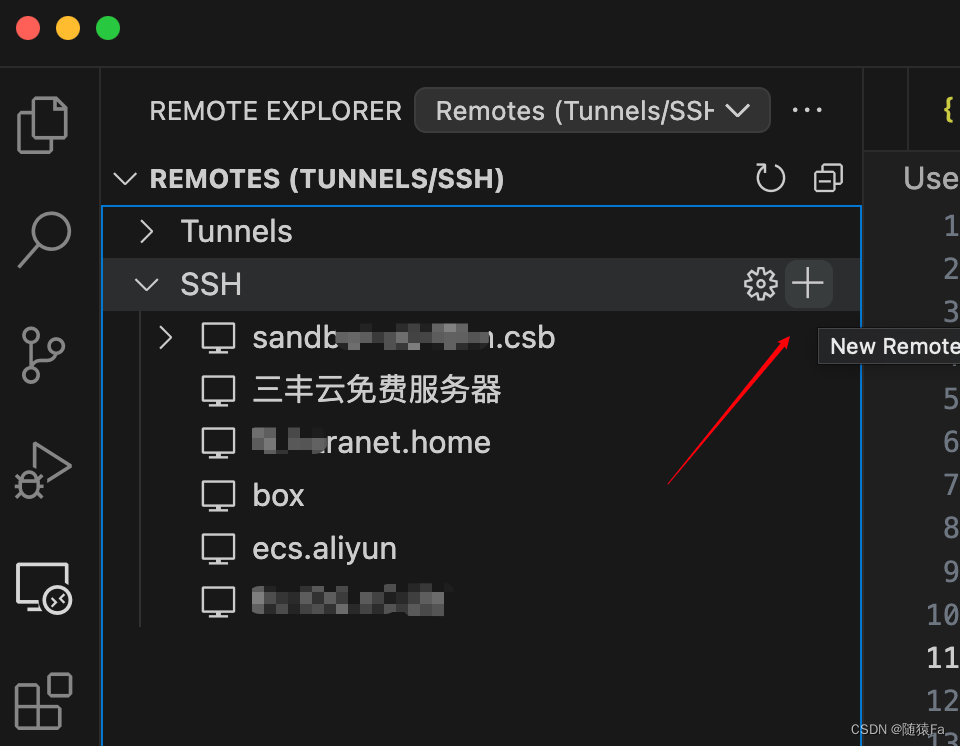
远程开发之vacode插件Remote - SSH
远程开发之vacode插件Remote - SSH vscode插件(Remote - SSH)ssh config自定义配置跳板机ssh-agent配置(使ForwardAgent配置生效, 免密拉代码)拷贝公钥到服务器(实现免密登录服务器) 通过vscode的Remote - SSH插件, 实现远程服务器进行像本地操作一样使用远程服务器, 亦可进行像…...

大模型实战营Day4 作业
基础作业: 构建数据集,使用 XTuner 微调 InternLM-Chat-7B 模型, 让模型学习到它是你的智能小助手,效果如下图所示,本作业训练出来的模型的输出需要将不要葱姜蒜大佬替换成自己名字或昵称! 微调前(回答比较…...
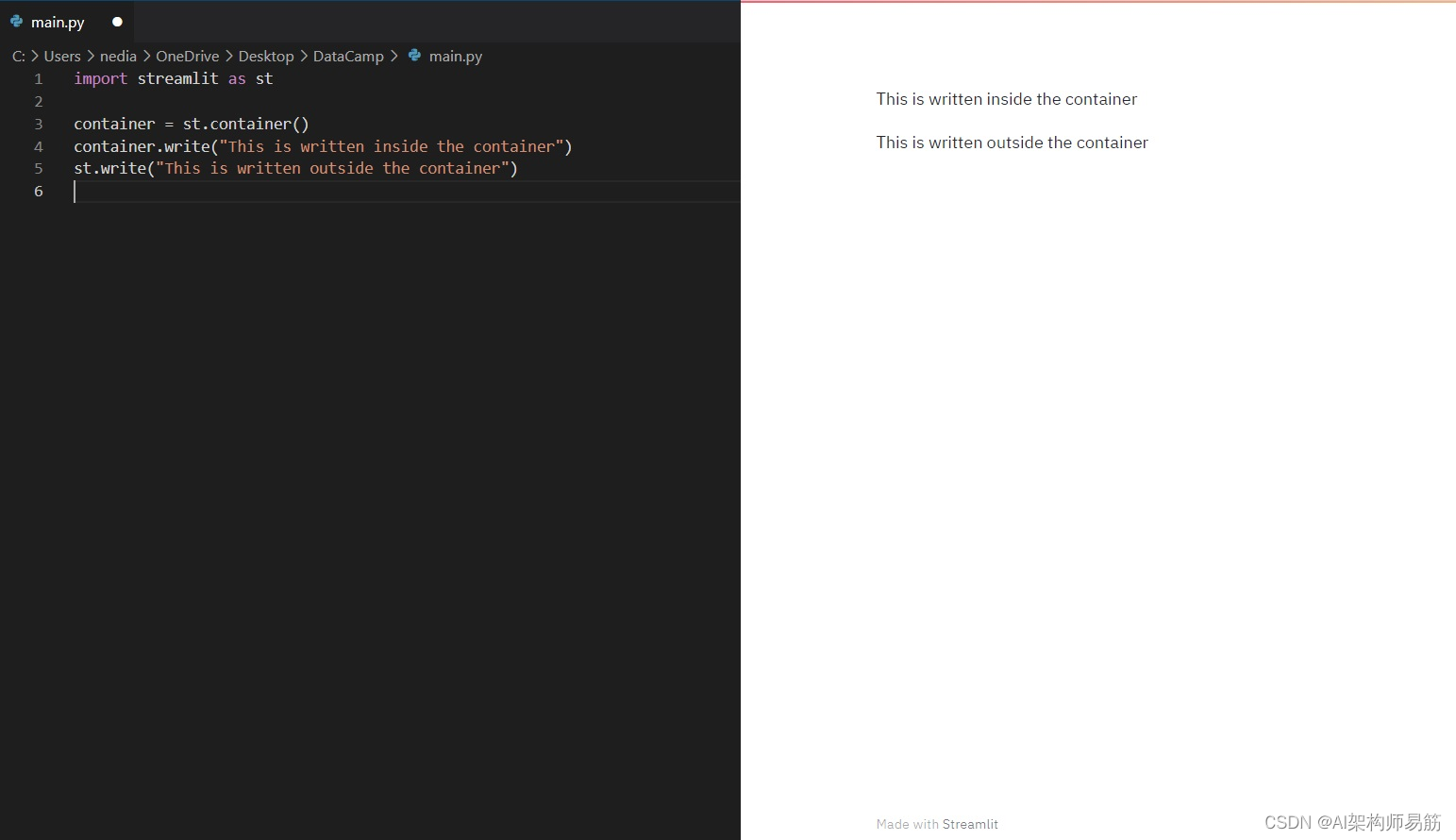
翻译: Streamlit从入门到精通 基础控件 一
这个关于Streamlit的教程旨在帮助数据科学家或机器学习工程师,他们不是网络开发者,也不想花费数周时间学习使用这些框架来构建网络应用程序。 1. 什么是Streamlit? Streamlit是一个免费且开源的框架,用于快速构建和共享美观的机器…...
【复现】网康科技-防火墙存在RCE漏洞_17
目录 一.概述 二 .漏洞影响 三.漏洞复现 1. 漏洞一: 四.修复建议: 五. 搜索语法: 六.免责声明 一.概述 网康下一代防火墙(NGFW)是一款可以全面应对应用层威胁的高性能防火墙。通过深入洞察网络流量中的用户、应用和内容,并…...
vue2、vue3里面去掉访问地址中路由‘#‘号--nginx配置
需求 我们这里分享一下关于Vue2和Vue3里面如何去掉浏览器路由里面#号的问题,以及nginx的配置。 去掉#号问题之前我们先讨论一下html中的hash模式和history模式。 html中的hash模式 HTML的hash模式指的是URL中的锚点部分(#后面的内容)被用…...

AR HUD全面「上新」
AR HUD赛道正在迎来新的时代。 上周,蔚来ET9正式发布亮相,新车定位为D级行政旗舰轿车,其中,在智能座舱交互层面,继理想L系列、长安深蓝S7之后,也首次取消仪表盘,取而代之的是业内首个全焦段AR H…...
Open3D AABB包围盒计算与使用(19)
Open3D AABB包围盒计算与使用(19) 一、算法速览二、算法实现1.代码2.结果少年听雨歌楼上。红烛昏罗帐。壮年听雨客舟中。江阔云低、断雁叫西风。 而今听雨僧庐下。鬓已星星也。悲欢离合总无情。一任阶前、点滴到天明。 一、算法速览 AABB包围盒就是将点云用一个各条边沿着坐…...
HDFS相关API操作
文章目录 API文档环境配置API操作准备工作创建文件夹文件上传文件下载文件删除文件的更名和移动获取文件详细信息 API文档 HDFS API官方文档:https://hadoop.apache.org/docs/r3.3.1/api/index.html 环境配置 将Hadoop的Jar包解压到非中文路径(例如D:…...

【AI视野·今日Robot 机器人论文速览 第七十二期】Mon, 8 Jan 2024
AI视野今日CS.Robotics 机器人学论文速览 Mon, 8 Jan 2024 Totally 13 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers Deep Reinforcement Learning for Local Path Following of an Autonomous Formula SAE Vehicle Authors Harvey Merton, Thoma…...
)
背包问题(补充中)
1.01背包 有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。 第 i 件物品的体积是 v[i],价值是 w[i]。 求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出最大价值。 对于01背包问题,只有…...

十三、QPalette的简单使用(Qt5 GUI系列)
目录 一、设计需求 二、实现代码 三、代码解析 四、总结 一、设计需求 在实际应用中,经常需要改变某个控件的颜色外观,如背景、文字颜色等。Qt提供的调色板类 QPalette 专门用于管理对话框的外观显示。QPalette 类相当于对话框或是控件的调色板&…...

uniapp小程序超出一行显示...并展示更多按钮
注意:全部标签需要浮动在父盒子右边哦 循环获取所有需要展示数据标签的高度 this.goods this.goods.map(item > ({...item,showBtn: false}));this.$nextTick(() > {uni.createSelectorQuery().in(this).selectAll(".cart-info").boundingClientRect((data)…...
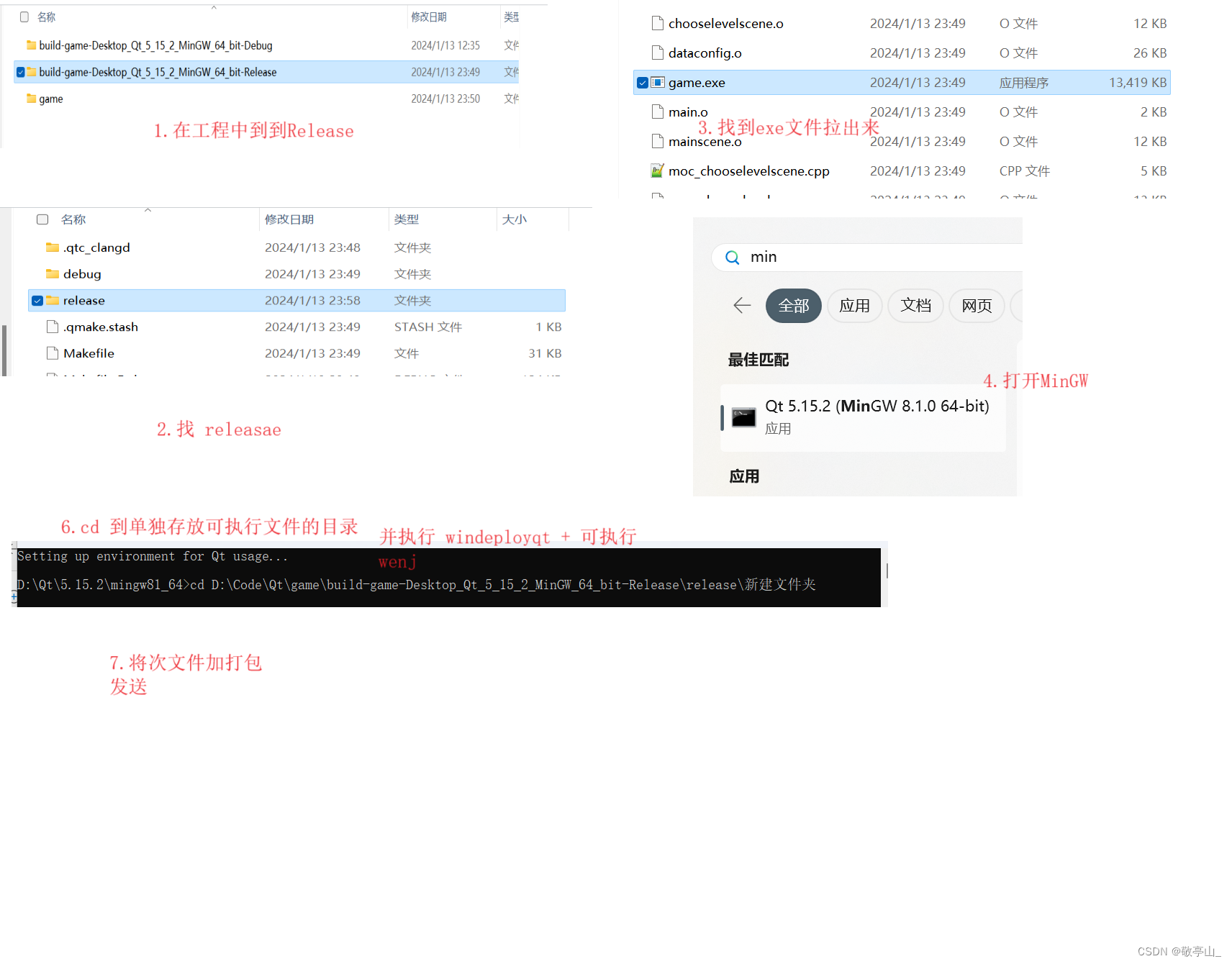
Qt打包程序
添加链接描述...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
