ITSS申报条件以及评审方式
01、四级申报基本条件:
(1)具有独立法人地位;
(2)已按照《运维服务能力成熟度》四级特征和关键指标建立了运维服务能力体系,且已有效运行三个月以上;
(3)能够提供运维服务能力管理、人员、资源、技术和过程等有效证据;
(4)申请单位从事信息系统运维服务业务满6个月以上。
02、三级申报基本条件:
(1)具有独立法人地位;
(2)已按照《运维服务能力成熟度》三级特征和关键指标建立了运维服务能力体系,且已有效运行三个月以上;
(3)能够提供运维服务能力管理、人员、资源、技术和过程等有效证据;
(4)申请单位从事信息系统运维服务业务满1年以上。
03、二级申报基本条件:
(1)具有独立法人地位;
(2)已按照《运维服务能力成熟度》二级特征和关键指标建立了运维服务能力体系,且已有效运行三个月以上;
(3)能够提供运维服务能力管理、人员、资源、技术和过程等有效证据;
(4)申请单位持有《信息技术服务标准ITSS符合性证书》(运维服务能力成熟度三级)满一年以上。
04、一级申报基本条件:
(1)具有独立法人地位;
(2)已按照《运维服务能力成熟度》一级特征和关键指标建立了运维服务能力体系,且已有效运行六个月以上;
(3)能够提供运维服务能力管理、人员、资源、技术和过程等有效证据;
(4)申请单位持有《信息技术服务标准ITSS符合性证书》(运维服务能力成熟度二级)满三年以上。
ITSS评审方式
ITSS分会组织评审和确认,其中:
1、四级:对材料进行形式审查和确认。
2、三级:组织专家以材料审查方式进行评审和确认;
3、二级:组织专家以材料审查、现场答辩等方式进行综合评审和确认;
4、一级:组织专家以材料审查、现场答辩等方式进行综合评审和确认;
未通过评审和确认的二级、三级申请单位,可接受降级或申请三个月整改,整改期满后由评估机构重新申报;仍未通过评审和确认的二级、三级申请单位,可接受降级或申请六个月整改,整改期满后由评估机构重新申报;连续三次未通过评审和确认的二级、三级申请单位,只能降级或重新申请评估。申请单位整改并重新申报的前提必须确保评估报告在有效期内;
ITSS分会在www.itss.cn官方网站公示评估和确认结果,经公示无异议后,向申请单位颁发
相关文章:

ITSS申报条件以及评审方式
01、四级申报基本条件: (1)具有独立法人地位; (2)已按照《运维服务能力成熟度》四级特征和关键指标建立了运维服务能力体系,且已有效运行三个月以上; (3)能…...

Qt中QByteArray之元素访问
访问QByteArray类对象中的某个元素主要有4种方式,分别为[]、at()、 data[]和constData[]。其中,[]和data]]方式为可读可写,at()和constData[]方式仅为可读。如果只是进行读操作,则通过at()和constData[]方式的访问速度最快,因为避…...
java实现教务管理系统
git地址:https://gitee.com/myshort-term/school-management 1.系统简介 开发教务管理系统程序,设计了ems(EMSApp)、dao(AssignmentDAO、CourseDAO、DeptDAO、ScoreDAO、UserDAO、EmailDAO)、domain&#…...
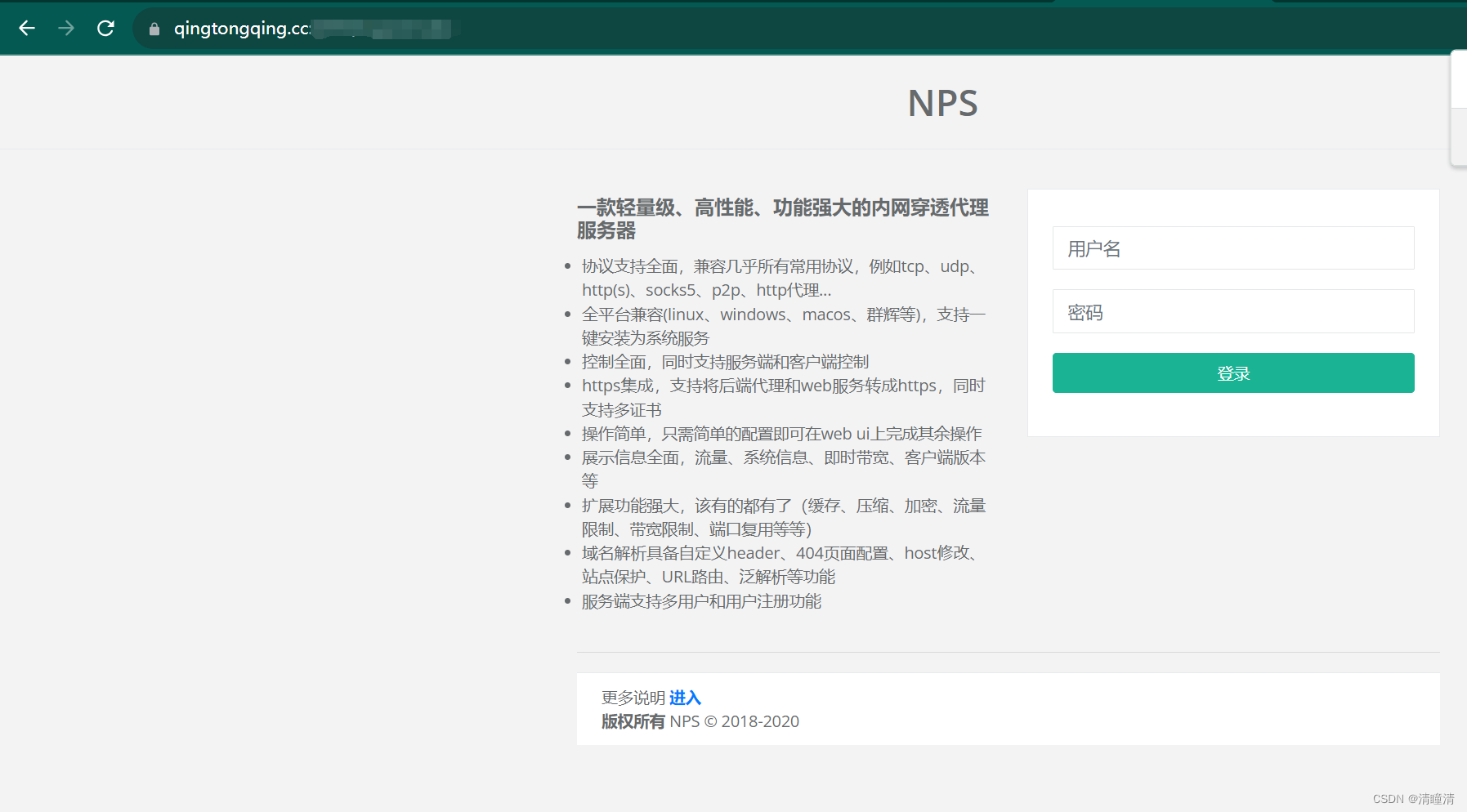
NPS配置https访问web管理页面
因为NPS默认也支持http的访问,所以在部署完后就一直没在意这个事情。 因为服务器是暴露在公网内的,所以还是要安全一点才行。不然一旦远控的机器被破解了就很危险了 一、使用nginx反向代理访问 1、首先在nps的配置文件里关闭使用https选项,…...
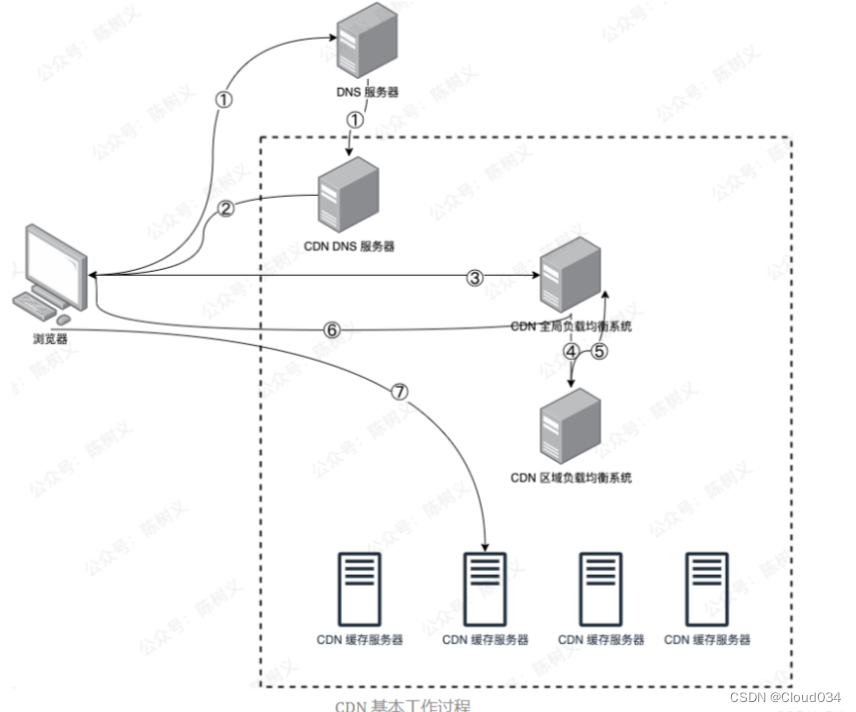
nginx和CDN应用
一、代理的工作机制 1.代替客户机向网站请求数据,从而可以隐藏用户的真实IP地址。 2.将获得的网页数据(静态 Web 元素)保存到缓存中并发送给客户机,以便下次请求相同的数据时快速响应。 二、代理服务器的…...

Keil5如何生成反汇编文件
Keil5如何生成反汇编文件 在Keil5界面下点击选项,选择“User”,勾选“After Build/Rebuild”中“RUN #1”,复制fromelf --text -a -c --outputxxx.dis xxx.axf 在Linker栏中找到“Linker Control string”里最后-o后的.axf文件,将…...
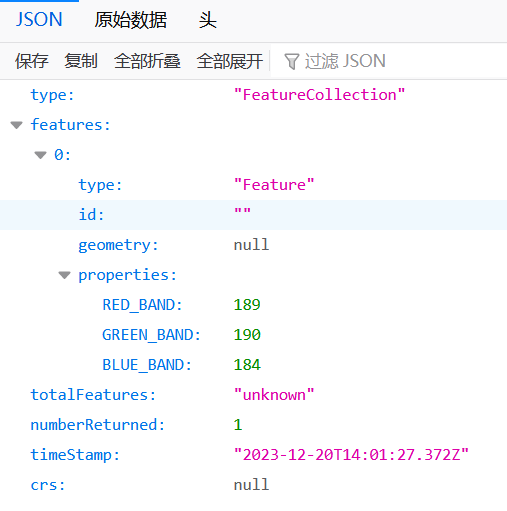
网络地图服务(WMS)详解
文章目录 1.概述2.GetCapabilities3.GetMap4.GetFeatureInfo 阅读本文之前可参考前文:《地图服务器GeoServer的安装与配置》与《GeoServer发布地图服务(WMS、WFS)》。 1.概述 经过前文的介绍,相信我们对WMS/WFS服务已经有了一个非…...
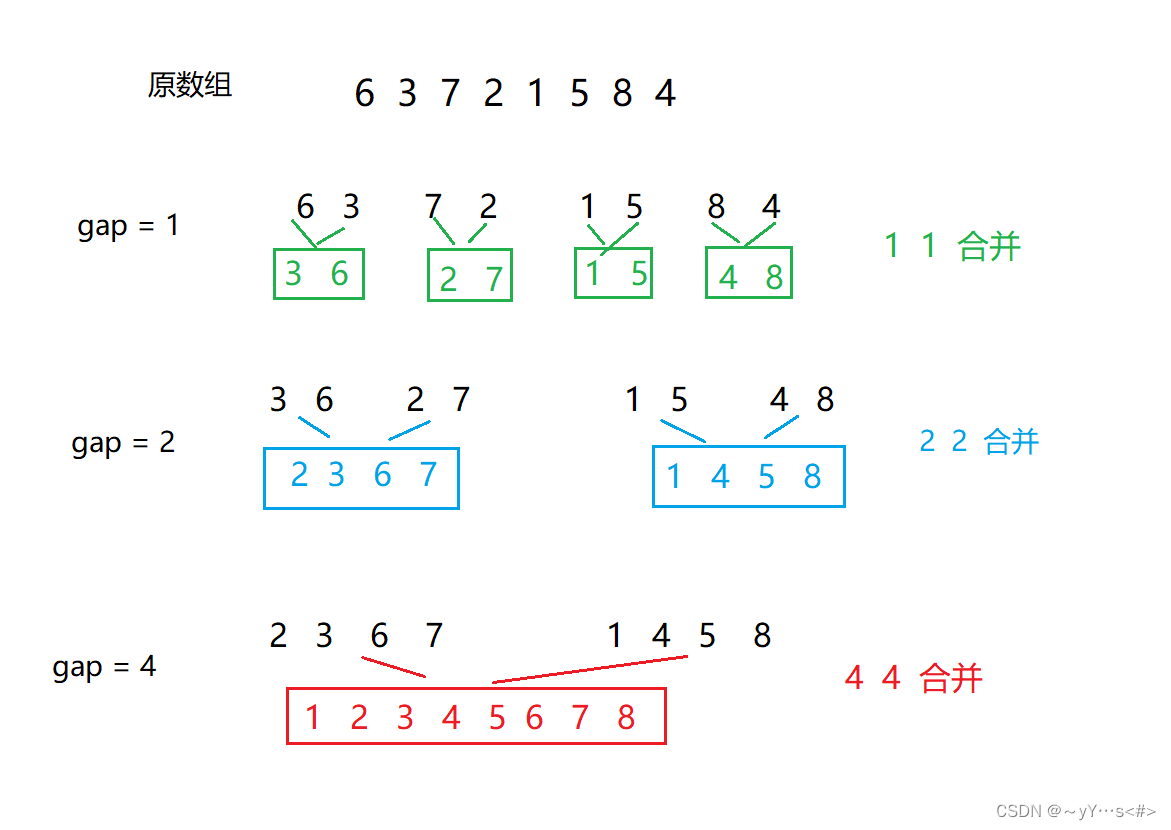
【排序篇3】快速排序、归并排序
目录 一、快速排序1.1 递归1.2 非递归 二、归并排序2.1 递归2.2 非递归 一、快速排序 1.1 递归 快速排序的递归采用二叉树的前序遍历的思路,单趟排序先确定好一个元素的位置,然后往后递归再确定其他子区域内的某个元素的位置,直到只有一个元…...

Python中的@property
在 Python 中,property 是一种装饰器,用于将一个方法转换成只读属性。通过使用 property 装饰器,你可以定义一个类的方法,使其在访问时可以像访问属性一样,而不是通过方法调用。 下面是一个简单的例子来说明 property …...
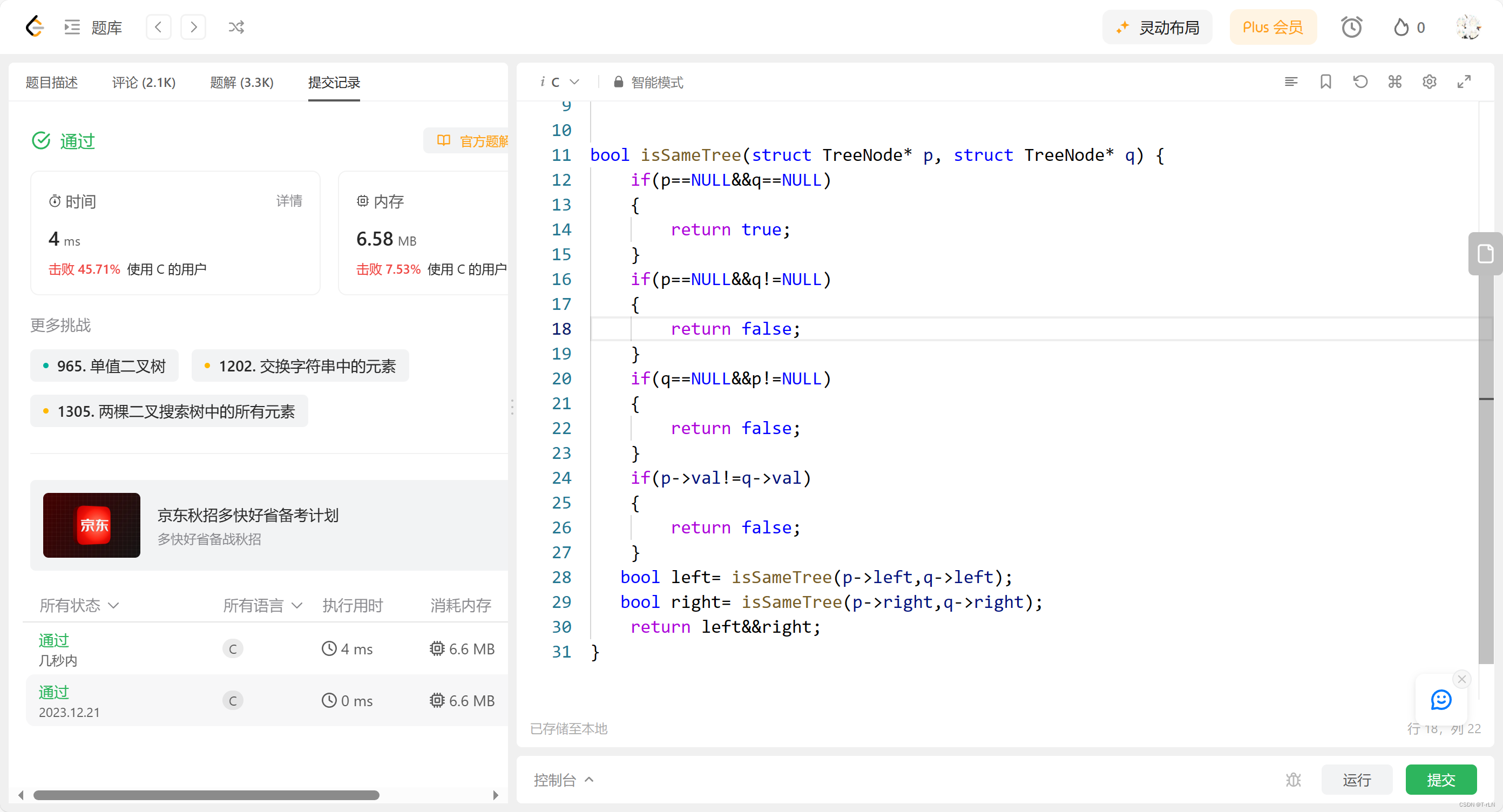
二叉树基础oj练习(单值二叉树、相同的树、二叉树的前序遍历)
讲了这么多数据结构相关的知识(可以看我的数据结构文章专栏): 抓紧刷题巩固一下了 目录 1.单值二叉树 题目描述 思路1 代码1 思路2 代码2 2.相同的树 题目描述 思路 代码 3.二叉树的前序遍历 代码 思路 1.单值二叉树 965. 单值二叉树 - 力扣(LeetCod…...
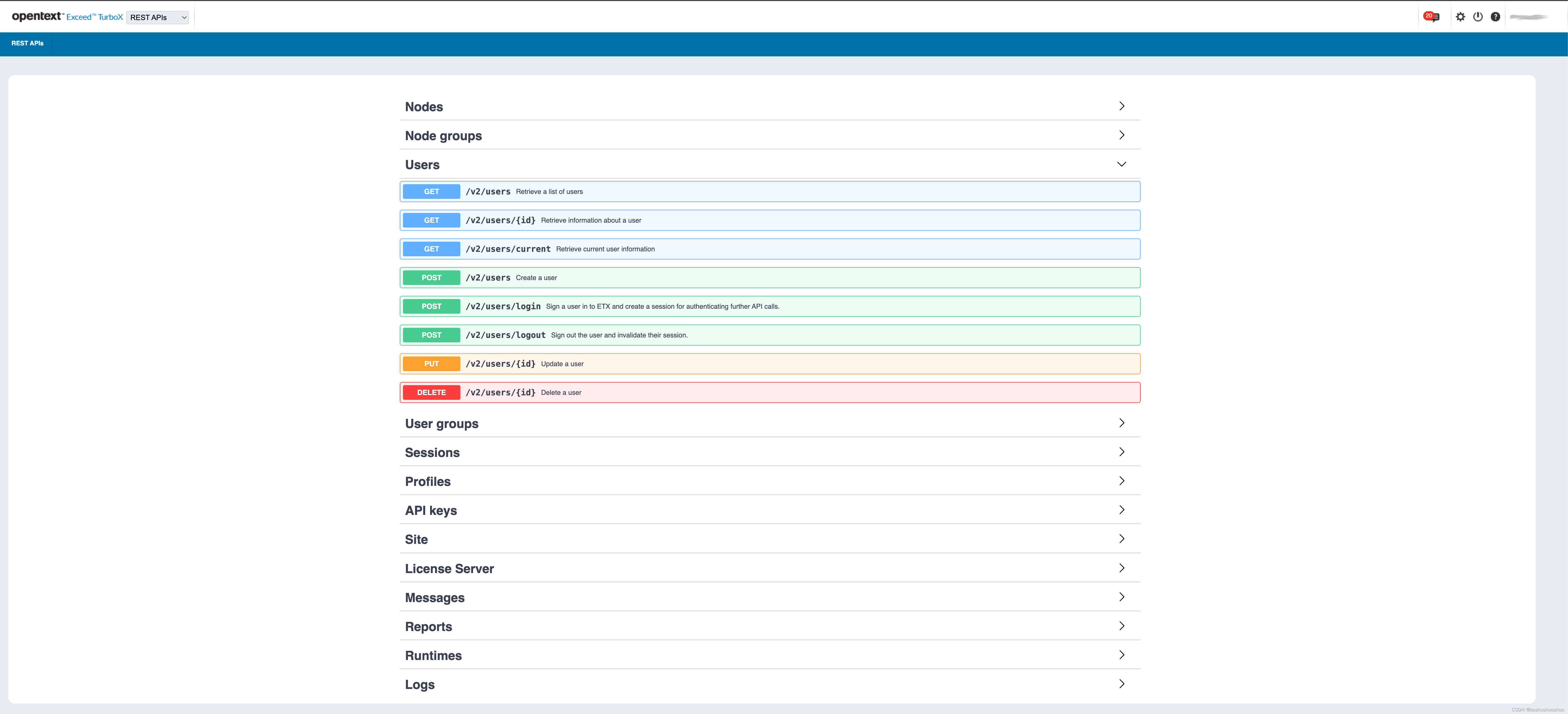
自动化创建ETX用户帐号
在芯片设计行业,ETX是常见的远程访问环境。用户在通过ETX访问远程环境前必须首先加入ETX系统,然后通过profile分配相关的环境的访问权限。 通常这些操作在ETX WEB页面手工操作,如果我们期望实现用户帐号注册全自动化,就需要将以上…...

Android 实现集合去重的方法
方法一:使用HashSet 将集合转换为HashSet。 Set<String> set new HashSet<>(list);将HashSet转换回List。 List<String> uniqueList new ArrayList<>(set);方法二:使用Java 8的Stream API 将列表转换为Stream。 Stream&l…...
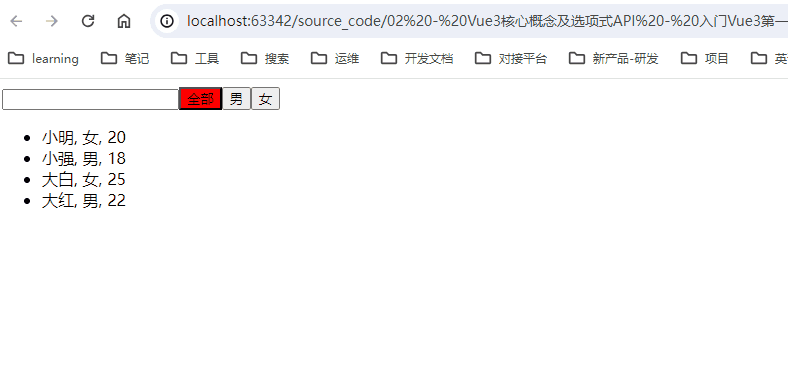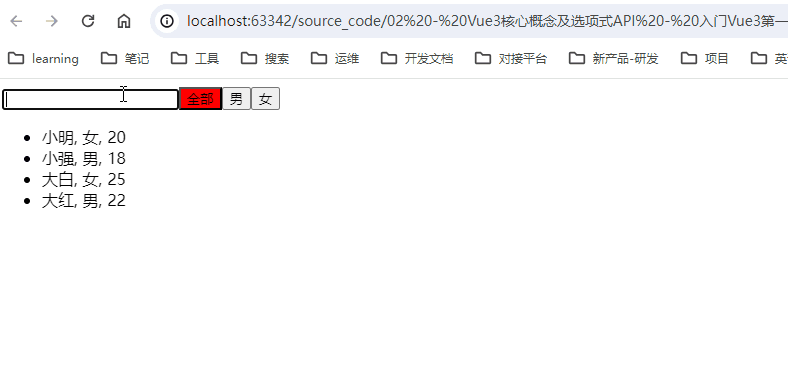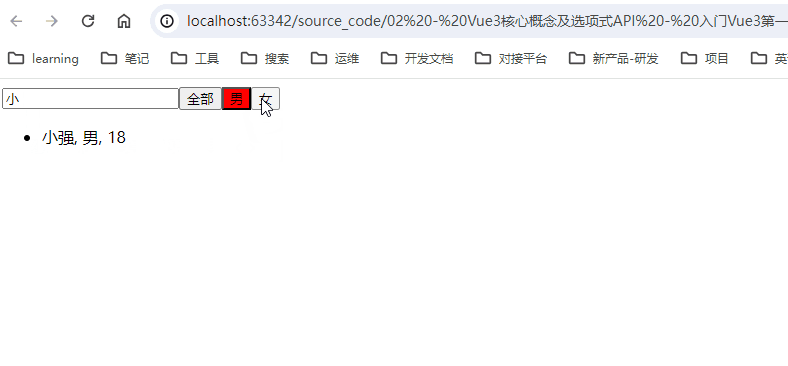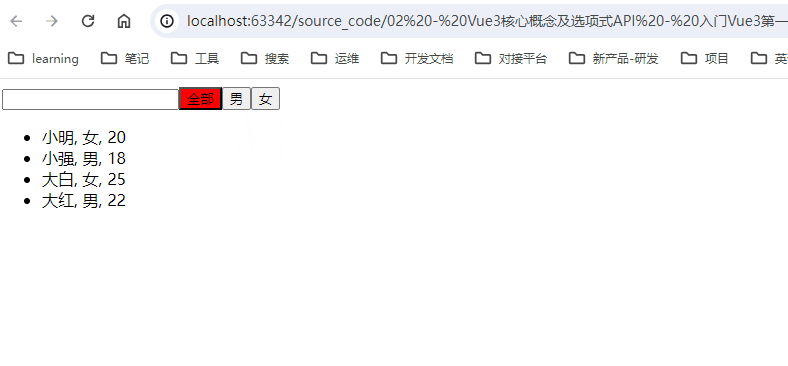
【Vue3】2-12 : 【案例】搜索关键词加筛选条件的综合
本书目录:点击进入 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 1.2、效果 1.3、json数据 - 02-data.json 1.4、代码 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 计算属性 - 绑定list,并过滤 input 双向绑定 - 当input改变时&…...
unity小程序websocket:nginx配置https (wss)转http (ws)及其他问题解决
目录 前言 实际运用场景 处理流程如下 nginx配置ssl和wss 配置过程中遇到的问题 1、无法连接服务器 2、通过IP可以访问,域名却不行 问题描述 解决 3、如何判断该域名是否备案了 前言 为了服务器网络的通用性,我们在实现移动端的游戏转微信小程序…...

MySql数据库对接Orcal数据库,需要考虑的前提问题
1.主表 从表的表关系;主键id 的关联问题; 2.字段类型的一致性问题(备注:像varchar类型的一点要谨防数据过长抛错); 3.实体类字段两表一致性问题; 4.入表不为空问题,判空尽量在实体…...

K8S的存储卷---数据卷
容器内的目录和宿主机的目录进行挂载 容器在系统上的生命周期是短暂的。delete,K8S用控制器创建的pod,delete相当于重启,容器的状态也会恢复到初始状态。一旦回到初始状态,所有的后天编辑的文件都会消失 容器和节点之间创建一个…...

【量化交易故事】小明开启了量化创业之旅-01
故事开始于2023年的春天,小明是一位对金融市场充满热情的IT工程师。在经历了数次基于主观判断和个人情绪进行投资却收获平平后,他意识到传统交易方式中的人为因素难以避免,而这往往成为影响投资决策稳定性和准确性的关键障碍。在一次偶然的机…...

ffmpeg写YUV420文件碰到阶梯型横线或者条纹状画面的原因和解决办法
版权声明:本文为CSDN博主「文三~」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/asdasfdgdhh/article/details/112831581 看到了,转载,留着备份…...
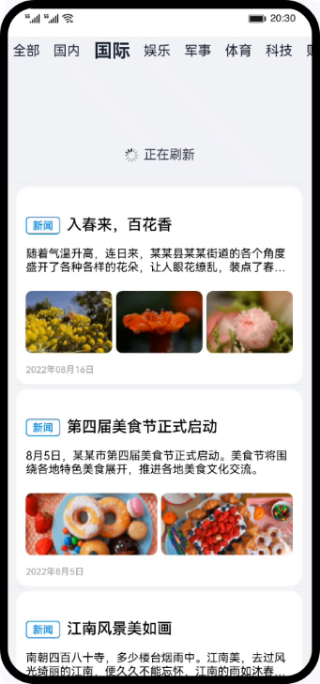
案例:新闻数据加载
文章目录 介绍相关概念相关权限约束与限制完整示例 代码结构解读构建主界面数据请求下拉刷新总结 介绍 本篇Codelab是基于ArkTS的声明式开发范式实现的样例,主要介绍了数据请求和touch事件的使用。包含以下功能: 数据请求。列表下拉刷新。列表上拉加载…...
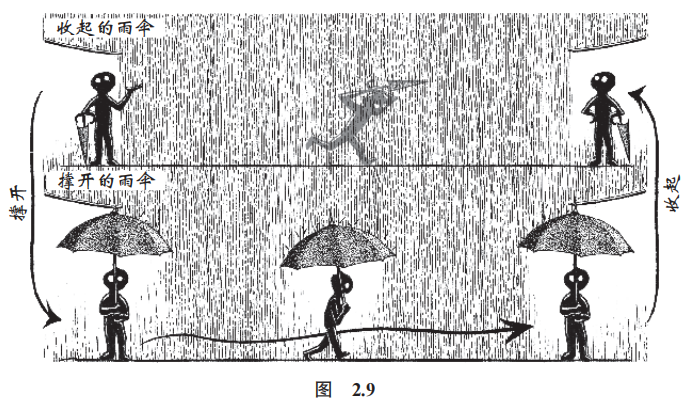
数学的雨伞下:理解世界的乐趣
这本书没有一个公式,却讲透了数学的本质! 《数学的雨伞下:理解世界的乐趣》。一本足以刷新观念的好书,从超市到对数再到相对论,娓娓道来。对于思维空间也给出了一个更容易理解的角度。 作者:米卡埃尔•洛奈…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...
