【排序篇3】快速排序、归并排序
目录
- 一、快速排序
- 1.1 递归
- 1.2 非递归
- 二、归并排序
- 2.1 递归
- 2.2 非递归
一、快速排序
1.1 递归
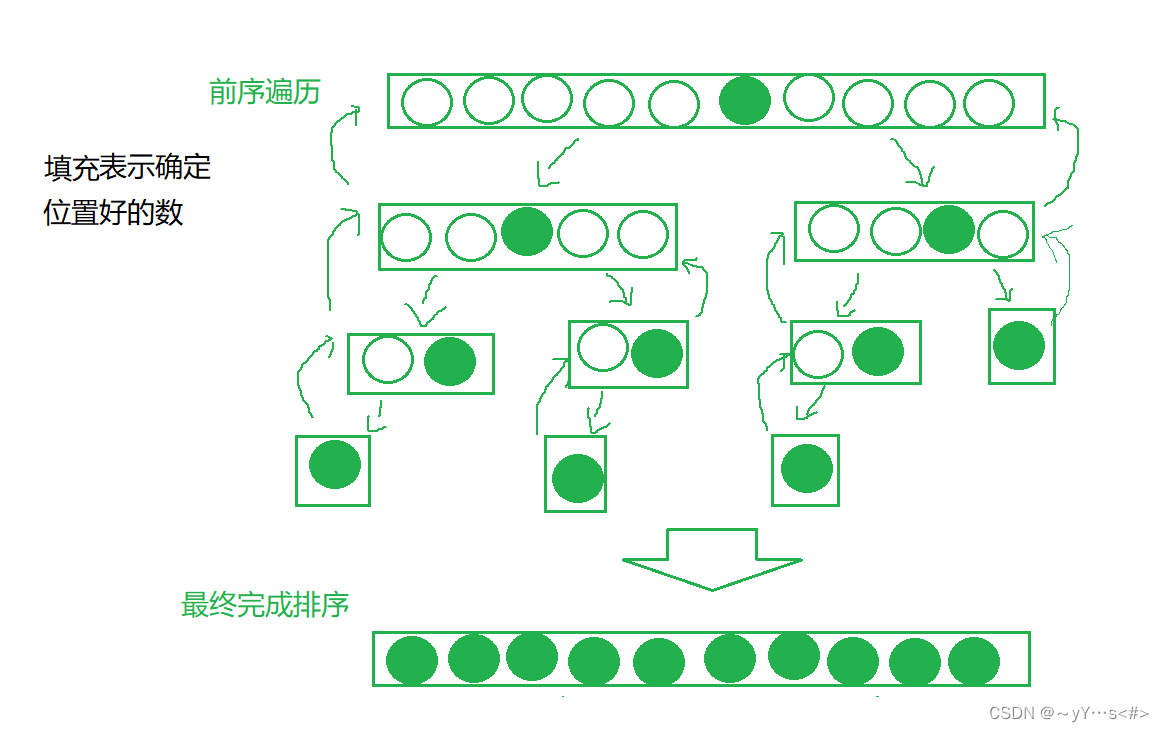
快速排序的递归采用二叉树的前序遍历的思路,单趟排序先确定好一个元素的位置,然后往后递归再确定其他子区域内的某个元素的位置,直到只有一个元素返回。
递归的图示:
代码:
void QuickSort(int* a, int begin, int end)
{//区间内小于等于1,就返回if (begin >= end){return;}//单趟排序,返回确定位置好的元素下标int ki = partsort1(a, begin, end);//递归 - 区间:[begin, ki-1],[ki+1, end]QuickSort(a, begin, ki - 1);QuickSort(a, ki + 1, end);
}
接下来分析单趟排序的实现。有3种方式:Hoare法、挖坑法、前后指针法。
1️⃣Hoare法
整体思路:
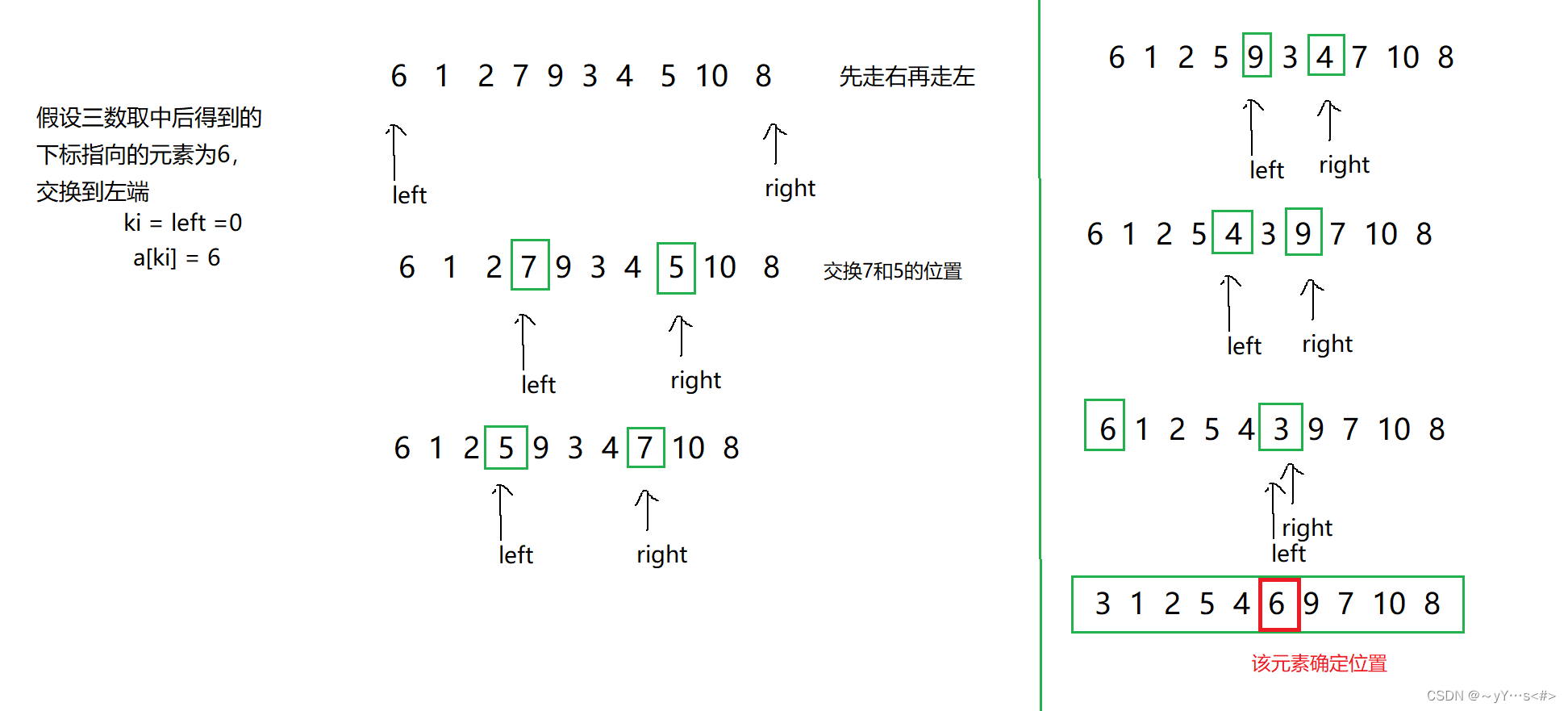
- 通过三数取中获取较靠中间元素的下标mid,然后mid指向的元素与左端的元素进行交换,防止极端情况
- 定义一个变量 ki = left 便于记录左端的值,注意ki是下标
- 先移动右边再移动左边,right指向的元素大于等于ki指向的元素就减1往前走,小于就停下;left指向的元素小于等于ki指向的元素就+1往后走,大于就停下,然后两者停下分别指向的元素进行交换,然后先走右再走左继续移动
- left与right相遇,跳出循环,交换ki指向的元素和left指向的元素,此时left指向的元素就是确定好位置的元素,最后返回下标left
图示:
代码:
//Hoare法
int partsort1(int* a, int left, int right)
{//获取较中间的元素的下标int mid = getmid(a, left, right);//三数取中Swap(&a[left], &a[mid]);//与左端交换,防止极端情况int ki = left;//注意ki得到的是下标while (left < right){//先走右再走左while (left < right && a[right] >= a[ki])//是大于等于往前走,小于就停下{ // 防止走的过程中越界right--;}while (left < right && a[left] <= a[ki])//是小于等于往前走,大于就停下{ // 防止走的过程中越界left++;}Swap(&a[left], &a[right]);//交换两个元素}Swap(&a[ki], &a[left]);//把ki指向的元素交换到它最终的位置return left;//返回确定位置的元素的下标
}
问题1:为什么要三数取中
因为三数取中可以防止出现极端情况,该极端情况指:ki指向的元素本来就应该放在左端,比如:
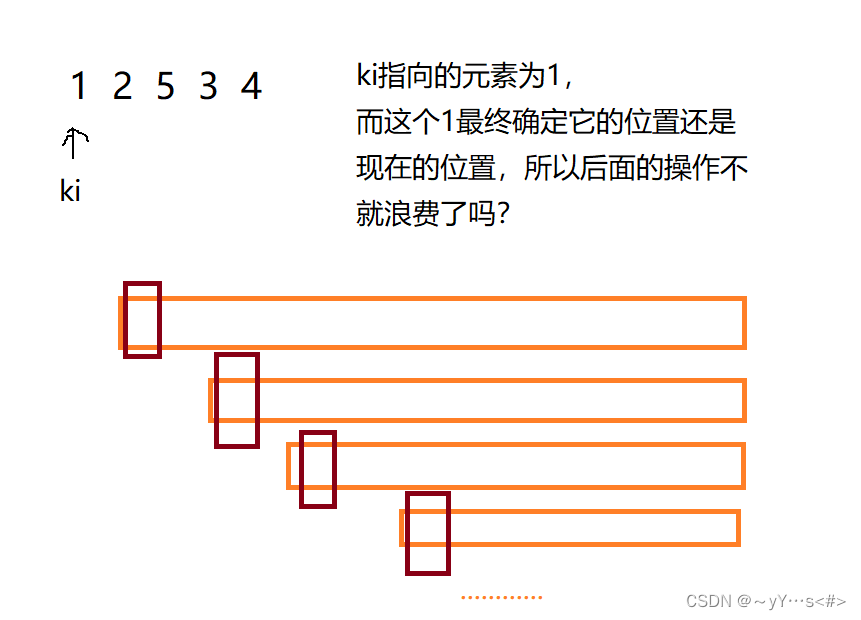
如果大部分是这种最坏情况,导致快速排序的复杂度为O(N ^ 2)
三数取中可以取到较靠中间位置的元素的下标,尽可能避免了以上情况,就算有个别还是在最左端,但是对整体的效率并没有多大影响。所以三数取中对快速排序的优化有很大的帮助。
代码:
//三数取中
int getmid(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right])return mid;else if (a[right] < a[left])return left;elsereturn right;}else{if (a[mid] > a[right])return mid;else if (a[right] > a[left])return left;elsereturn right;}
}
问题2:为什么ki取的是下标,不是数组元素
这与最后确定元素位置的交换有关,假设ki是数组元素,交换的是left指向的元素和ki,那么结果是left指向的元素变成了ki这个元素,但是数组左端的元素依旧没变。

ki取的是下标,才能真正交换数组左端和left指向的元素。
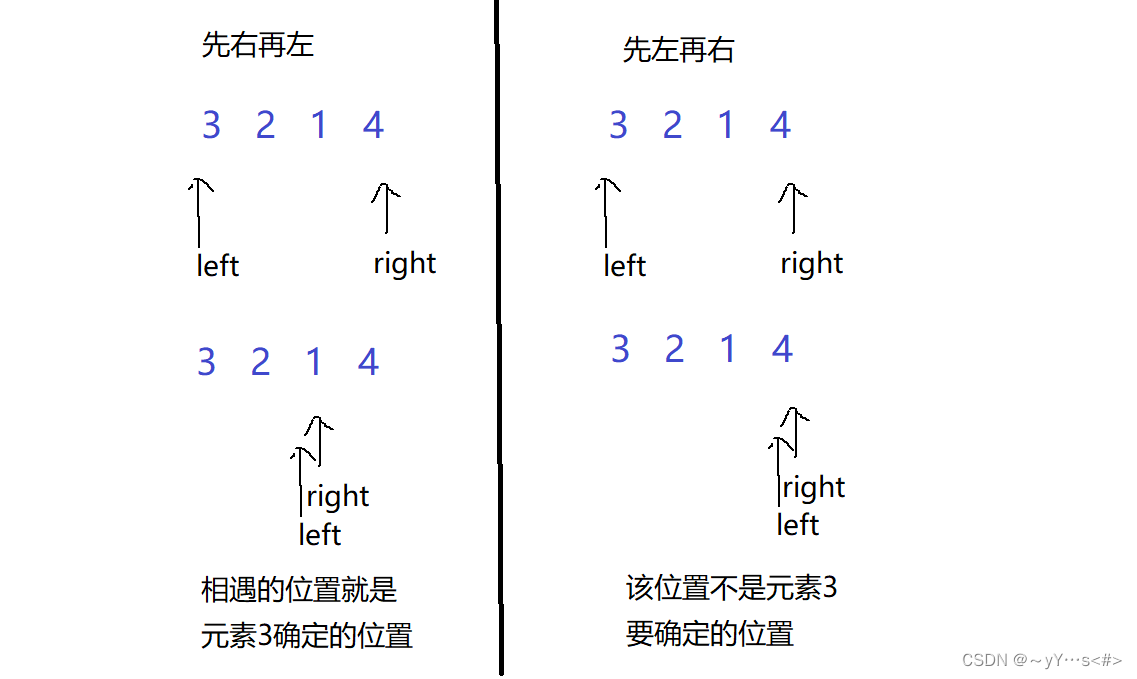
问题3:为什么先走右边,再走左边
举个栗子:
2️⃣挖坑法
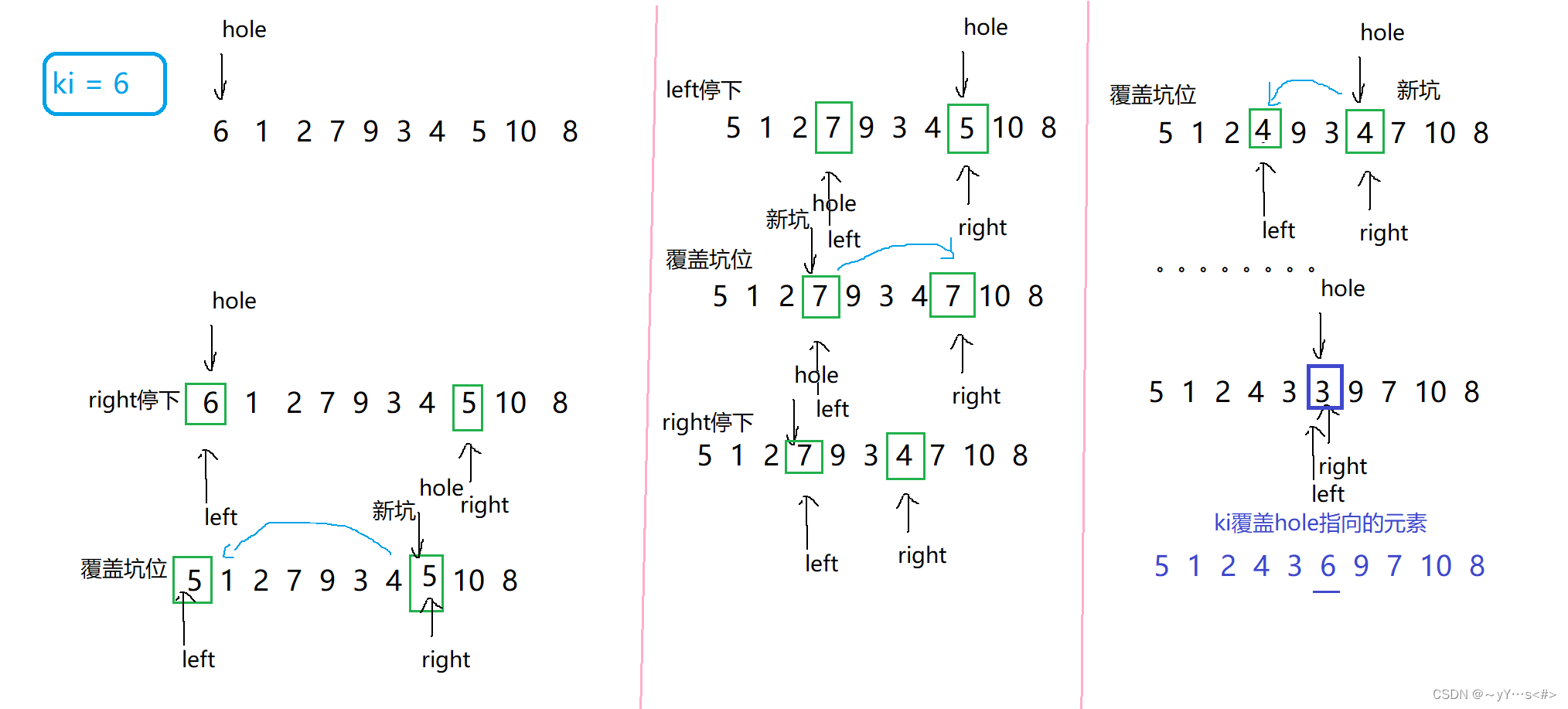
整体思路:
- 三数取中,与Hoare法的步骤一样
- ki取的是left指向的元素,为后面的填坑作准备
- 定义一个坑hole = left (是下标)
- 先走右边,停下后,将此时right指向的元素覆盖坑位的元素,然后产生新的坑位,right变成坑
- 再走左边,停下后,将此时left指向的元素覆盖坑位的元素,然后产生新的坑位,left变成坑
- 循环全部走完后,最终的hole就是ki要确定的位置,覆盖坑位,然后返回hole
图示:
代码:
//挖坑法
int partsort2(int* a, int left, int right)
{//获取较中间的元素的下标int mid = getmid(a, left, right);//三数取中Swap(&a[left], &a[mid]);//与左端交换,防止极端情况int ki = a[left];//注意ki得到的是数组元素int hole = left;//初始的坑的位置while (left < right){//先走右再走左while (left < right && a[right] >= ki)//是大于等于往前走,小于就停下{ // 防止走的过程中越界right--;}a[hole] = a[right];//覆盖坑位的元素hole = right;//产生新的坑位while (left < right && a[left] <= ki)//是小于等于往前走,大于就停下{ // 防止走的过程中越界left++;}a[hole] = a[left];//覆盖坑位的元素hole = left;//产生新的坑位}a[hole] = ki;//确定元素的位置return hole; //返回确定位置的元素的下标
}
3️⃣前后指针法
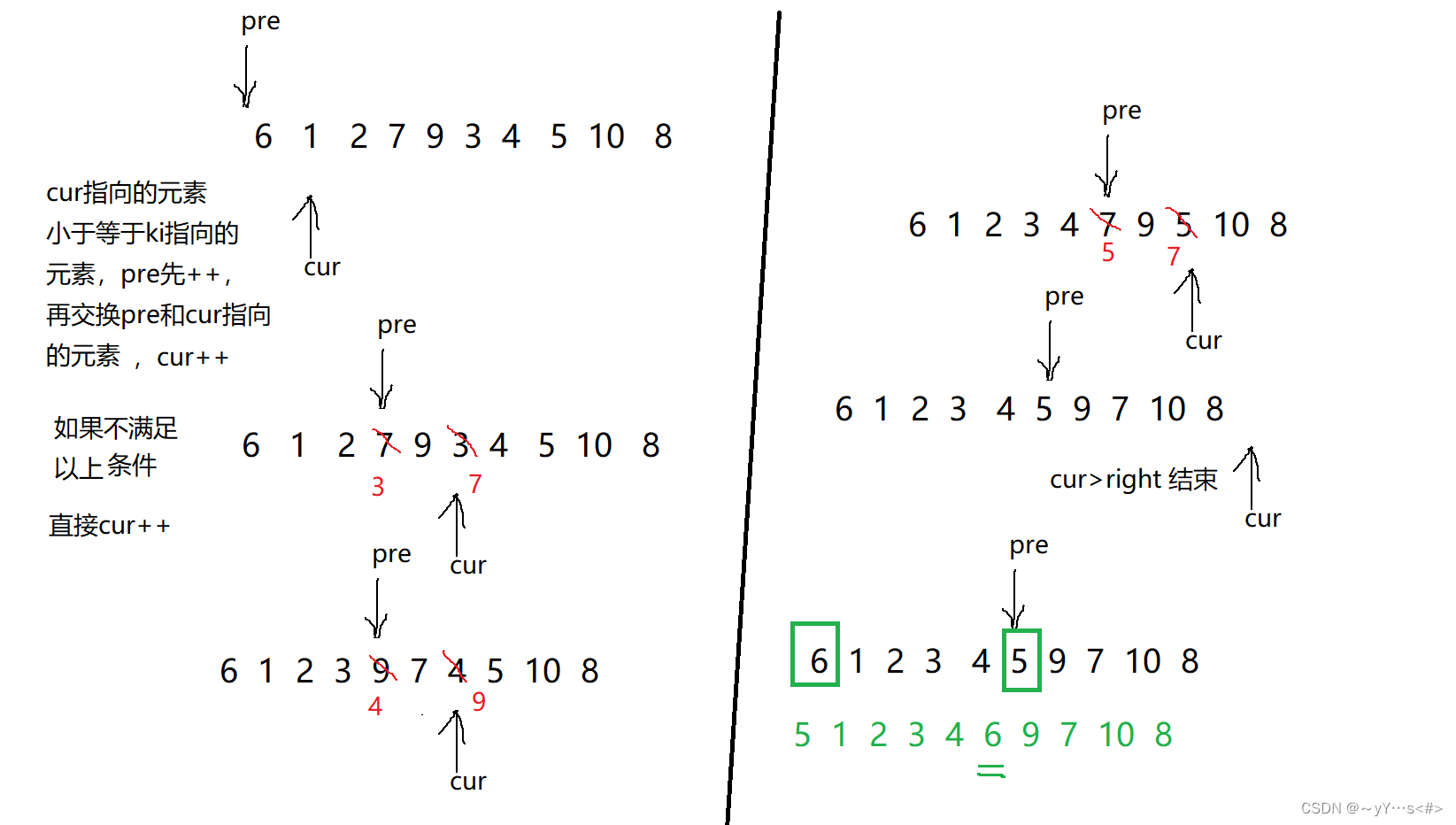
通过前面的两种方法可以发现:确定好某个元素的位置后,该元素的左右两个区间分别是小于这个元素和大于这个元素(以数组是1,2,3,4,5,6,7,8,9,10为例),也就是说要确定位置的元素是区分两个不同区间的标杆,所以这里可以使用前后指针法,用来区分两块区域。
整体思路:
- 定义前后指针,cur=left+1,pre = left
- 如果cur指向的元素小于等于ki指向的元素,pre先加1,再交换pre和cur分别指向的元素,然后cur++
- cur循环完,交换pre和ki分别指向的元素,pre的位置就是确定好的位置,然后返回pre
图示:
代码:
//前后指针法
int partsort3(int* a, int left, int right)
{int mid = getmid(a, left, right);//三数取中Swap(&a[left], &a[mid]);//与左端交换,防止极端情况int ki = left;//注意ki得到的是下标int cur = left + 1, pre = left;//定义前后指针while (cur <= right)//范围限制{if (a[cur] <= a[ki])//如果小于,先++pre再交换分别指向的元素{Swap(&a[++pre], &a[cur]);}cur++;//cur都要往后走}Swap(&a[ki], &a[pre]);//把ki指向的元素交换到它最终的位置return pre;//返回确定位置的元素的下标
}
1.2 非递归
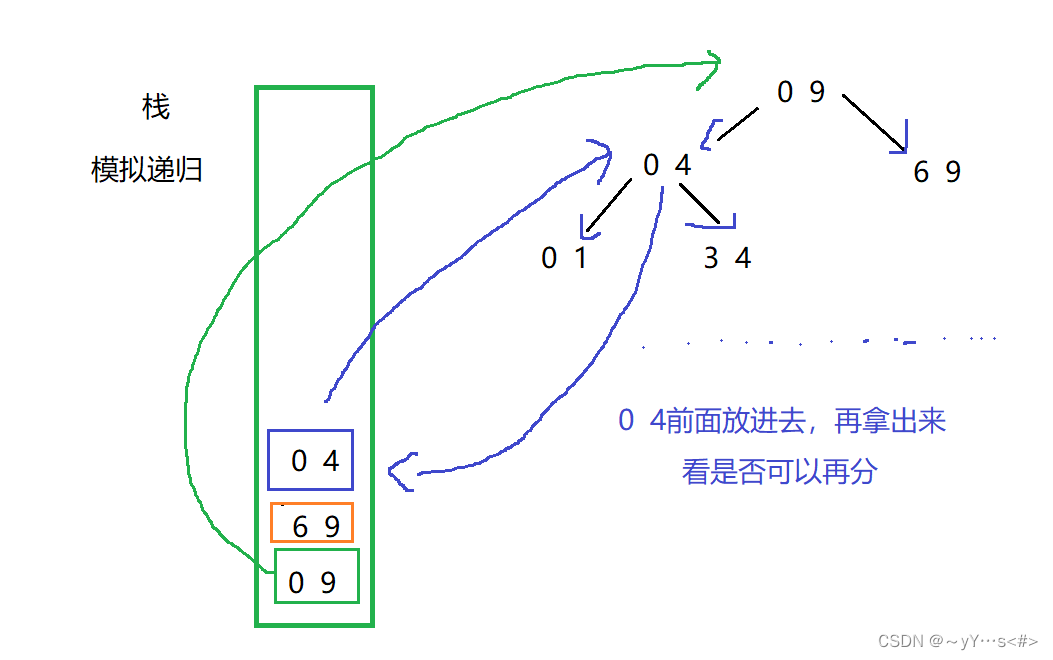
快速排序的非递归是用栈模拟递归来实现的,栈的特点是后进先出,递归是先左边再右边的,所以放入栈的数据应该先放右再放左,这样取数据才是先左再右。
图示:
代码:
//快速排序 - 非递归
void QuickSortNoR(int* a, int begin, int end)
{stack<int> st;//定义一个栈st.push(end);//先放右st.push(begin);//再放左while (!st.empty())//不为空进入循环{int left = st.top();//取左值st.pop();//删除栈顶元素int right = st.top();//取右值st.pop();//删除栈元素int ki = partsort3(a, left, right);//一趟排序确定某个元素的位置,返回该位置if (ki + 1 < right)//整体先放右{st.push(right);//里面先放右st.push(ki + 1);//里面再放左}if (left < ki - 1)//整体再放左{st.push(ki - 1);//里面先放右st.push(left);//里面再放左}}
}
快速排序特性总结:
- 时间复杂度:O(N * logN)
- 空间复杂度:O(logN)
- 不稳定
二、归并排序
2.1 递归
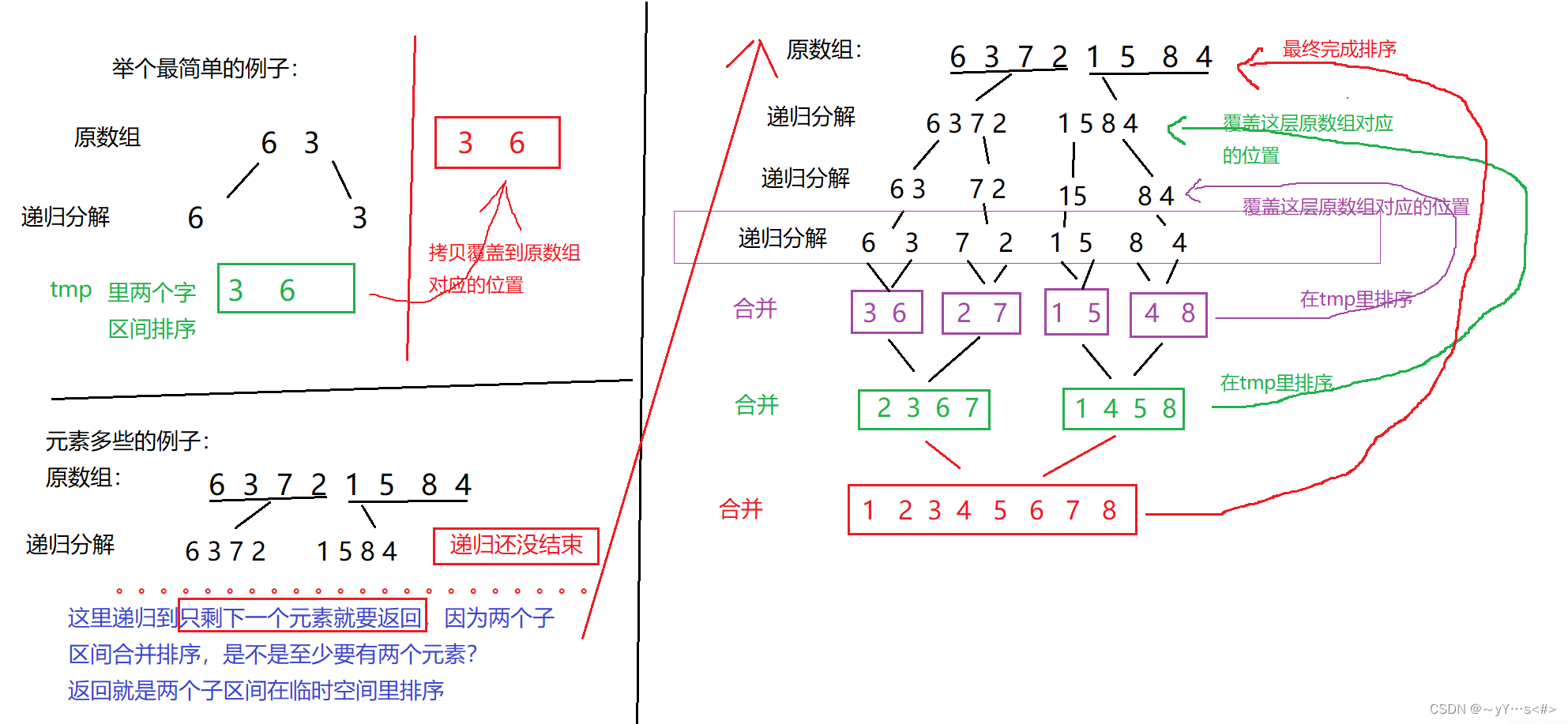
归并排序的递归采用二叉树的后序遍历的思想,先分解成小块区间,然后再合并两个小块空间的同时将这两块子区间的元素进行排序。依次类推。这里还要额外开辟一块临时空间,用来对两个子区间排序,在临时空间排完序后,然后把已经排序的元素的拷贝到原数组对应的位置,最终将整个数组排完序。
图示:
代码:
//归并排序-递归
void MergeSort(int* a, int* tmp, int begin, int end)
{//区间内元素个数小于等于1返回if (begin >= end){return;}int mid = (begin + end) / 2;//取划分区域的下标MergeSort(a, tmp, begin, mid);//递归左边MergeSort(a, tmp, mid + 1, end);//递归右边int begin1 = begin, end1 = mid;//合并的第一块小区间int begin2 = mid + 1, end2 = end;//合并的第二块小区间int k = begin;//注意k为begin当前区域的初始位置while (begin1 <= end1 && begin2 <= end2){ // 谁小谁先放入tmpif (a[begin1] <= a[begin2]){tmp[k++] = a[begin1++];}else{tmp[k++] = a[begin2++];}}// 哪块小区间有剩余,直接放入tmpwhile (begin1 <= end1){tmp[k++] = a[begin1++];}while (begin2 <= end2){tmp[k++] = a[begin2++];}//最后拷贝到原数组对应的位置,完成排序memcpy(a + begin, tmp + begin, sizeof(int) * (end2 - begin + 1));
}
2.2 非递归
归并排序的非递归也是模拟递归的过程,只是没有递,只有归,即只有合并的过程,用for循环控制合并区间的大小和范围即可,也要借助临时空间来排序,最后拷贝给原数组。
图示:
代码:
//归并排序-非递归
void MergeSortNoR(int* a, int* tmp, int n)
{int gap = 1;//初始合并的子区间大小while (gap < n)//范围{for (int i = 0; i < n; i += gap * 2){int begin1 = i, end1 = i + gap - 1;//合并的第一块小区间int begin2 = i + gap, end2 = i + gap * 2 - 1;//合并的第二块小区间int k = i;if (begin2 >= n)//只有第一块小区间,没有第二块小区间{break;//不能合并,跳出}if (end2 >= n)//第二块小区间个数较少,但是不影响合并{end2 = n - 1;//修改end2的值}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[k++] = a[begin1++];}else{tmp[k++] = a[begin2++];}}while (begin1 <= end1){tmp[k++] = a[begin1++];}while (begin2 <= end2){tmp[k++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));//排序+拷贝回原数组}gap *= 2;//区间增大}
}
注意:
上面的代码有两个特殊处理用于非2的次方个元素的数组,如果begin2大于等于n,说明要合并的两个子区间仅仅只有第一块小区间,没有第二块小区间,这时就不需要合并了(第一块小区间在之前已经合并为有序)。如果end2大于等于n,第二块小区间还是存在的,只是元素个数少些,这时就把end2的指向的位置该成第二块小区间内最后一个元素的位置即可。
归并排序特性总结:
- 归并排序要额外开辟一块空间用来处理排序的问题
- 时间复杂度:O(N * logN)
- 空间复杂度:O(N)
- 稳定
相关文章:

【排序篇3】快速排序、归并排序
目录 一、快速排序1.1 递归1.2 非递归 二、归并排序2.1 递归2.2 非递归 一、快速排序 1.1 递归 快速排序的递归采用二叉树的前序遍历的思路,单趟排序先确定好一个元素的位置,然后往后递归再确定其他子区域内的某个元素的位置,直到只有一个元…...

Python中的@property
在 Python 中,property 是一种装饰器,用于将一个方法转换成只读属性。通过使用 property 装饰器,你可以定义一个类的方法,使其在访问时可以像访问属性一样,而不是通过方法调用。 下面是一个简单的例子来说明 property …...
二叉树基础oj练习(单值二叉树、相同的树、二叉树的前序遍历)
讲了这么多数据结构相关的知识(可以看我的数据结构文章专栏): 抓紧刷题巩固一下了 目录 1.单值二叉树 题目描述 思路1 代码1 思路2 代码2 2.相同的树 题目描述 思路 代码 3.二叉树的前序遍历 代码 思路 1.单值二叉树 965. 单值二叉树 - 力扣(LeetCod…...
自动化创建ETX用户帐号
在芯片设计行业,ETX是常见的远程访问环境。用户在通过ETX访问远程环境前必须首先加入ETX系统,然后通过profile分配相关的环境的访问权限。 通常这些操作在ETX WEB页面手工操作,如果我们期望实现用户帐号注册全自动化,就需要将以上…...

Android 实现集合去重的方法
方法一:使用HashSet 将集合转换为HashSet。 Set<String> set new HashSet<>(list);将HashSet转换回List。 List<String> uniqueList new ArrayList<>(set);方法二:使用Java 8的Stream API 将列表转换为Stream。 Stream&l…...
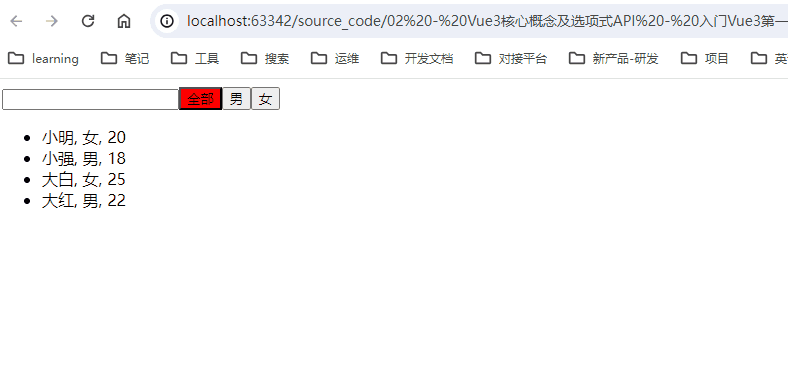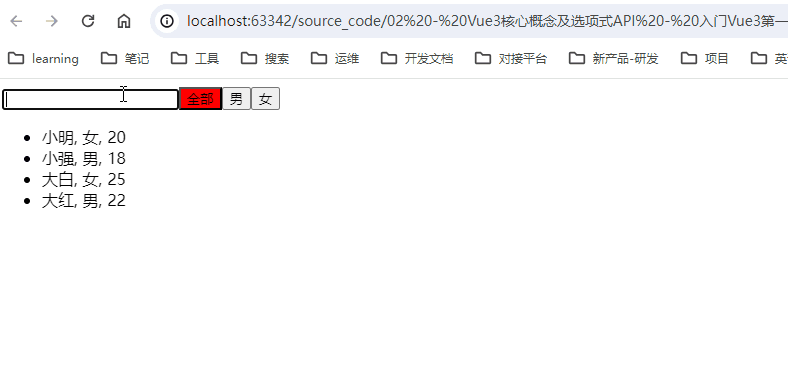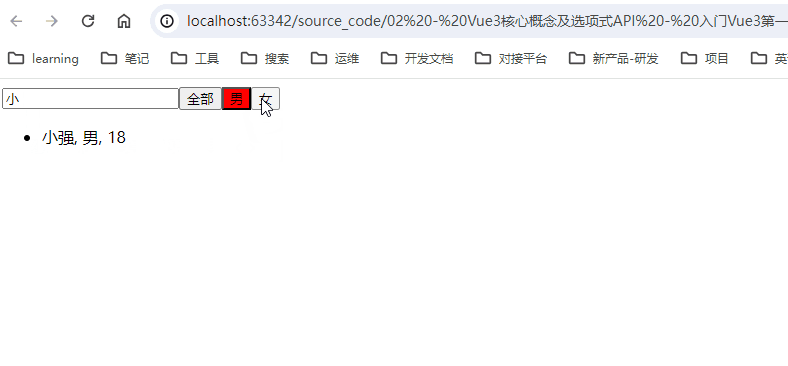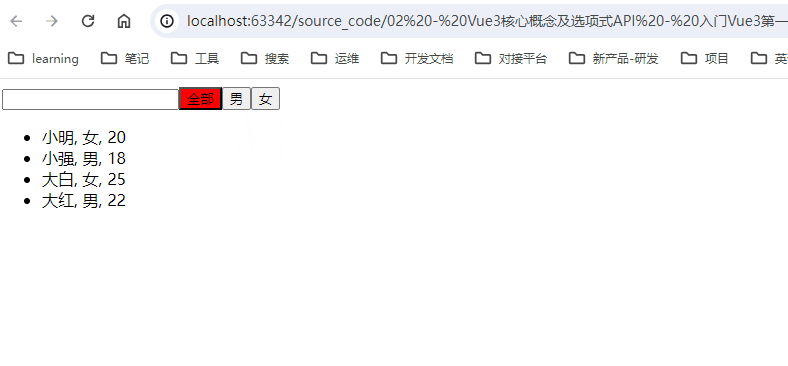
【Vue3】2-12 : 【案例】搜索关键词加筛选条件的综合
本书目录:点击进入 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 1.2、效果 1.3、json数据 - 02-data.json 1.4、代码 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 计算属性 - 绑定list,并过滤 input 双向绑定 - 当input改变时&…...
unity小程序websocket:nginx配置https (wss)转http (ws)及其他问题解决
目录 前言 实际运用场景 处理流程如下 nginx配置ssl和wss 配置过程中遇到的问题 1、无法连接服务器 2、通过IP可以访问,域名却不行 问题描述 解决 3、如何判断该域名是否备案了 前言 为了服务器网络的通用性,我们在实现移动端的游戏转微信小程序…...

MySql数据库对接Orcal数据库,需要考虑的前提问题
1.主表 从表的表关系;主键id 的关联问题; 2.字段类型的一致性问题(备注:像varchar类型的一点要谨防数据过长抛错); 3.实体类字段两表一致性问题; 4.入表不为空问题,判空尽量在实体…...

K8S的存储卷---数据卷
容器内的目录和宿主机的目录进行挂载 容器在系统上的生命周期是短暂的。delete,K8S用控制器创建的pod,delete相当于重启,容器的状态也会恢复到初始状态。一旦回到初始状态,所有的后天编辑的文件都会消失 容器和节点之间创建一个…...

【量化交易故事】小明开启了量化创业之旅-01
故事开始于2023年的春天,小明是一位对金融市场充满热情的IT工程师。在经历了数次基于主观判断和个人情绪进行投资却收获平平后,他意识到传统交易方式中的人为因素难以避免,而这往往成为影响投资决策稳定性和准确性的关键障碍。在一次偶然的机…...

ffmpeg写YUV420文件碰到阶梯型横线或者条纹状画面的原因和解决办法
版权声明:本文为CSDN博主「文三~」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/asdasfdgdhh/article/details/112831581 看到了,转载,留着备份…...
案例:新闻数据加载
文章目录 介绍相关概念相关权限约束与限制完整示例 代码结构解读构建主界面数据请求下拉刷新总结 介绍 本篇Codelab是基于ArkTS的声明式开发范式实现的样例,主要介绍了数据请求和touch事件的使用。包含以下功能: 数据请求。列表下拉刷新。列表上拉加载…...
数学的雨伞下:理解世界的乐趣
这本书没有一个公式,却讲透了数学的本质! 《数学的雨伞下:理解世界的乐趣》。一本足以刷新观念的好书,从超市到对数再到相对论,娓娓道来。对于思维空间也给出了一个更容易理解的角度。 作者:米卡埃尔•洛奈…...
)
补充 vue3用户管理权限(路由控制)
之前有人问我 ,如果是二级路由如何添加,这里我做一个补充吧。直接拿方法去用就行。也不做解释了。稍微看下就能看懂了 假设,后端返回给我们一个数据 [“/defa”,"/defa/defa1"] 这样的一个路由表,我们就需要通过这个路…...
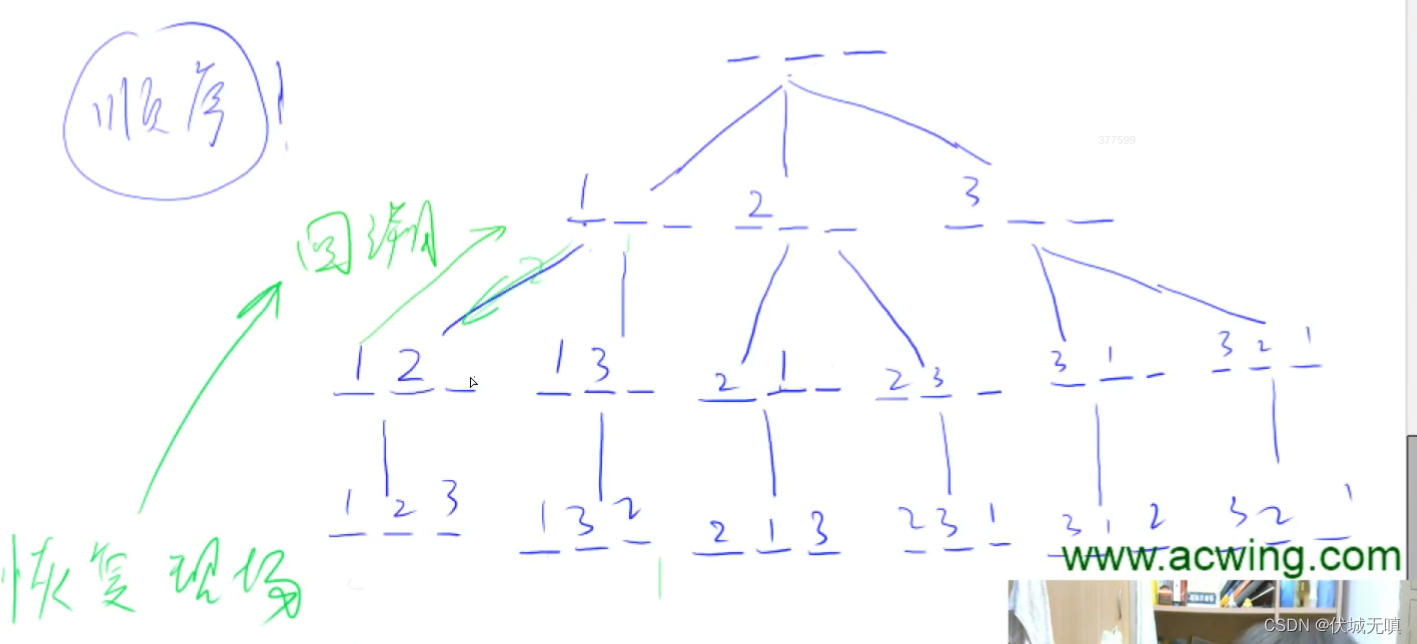
C++ 深度优先搜索DFS || 模版题:排列数字
给定一个整数 n ,将数字 1∼n 排成一排,将会有很多种排列方法。 现在,请你按照字典序将所有的排列方法输出。 输入格式 共一行,包含一个整数 n 。 输出格式 按字典序输出所有排列方案,每个方案占一行。 数据范围 1…...
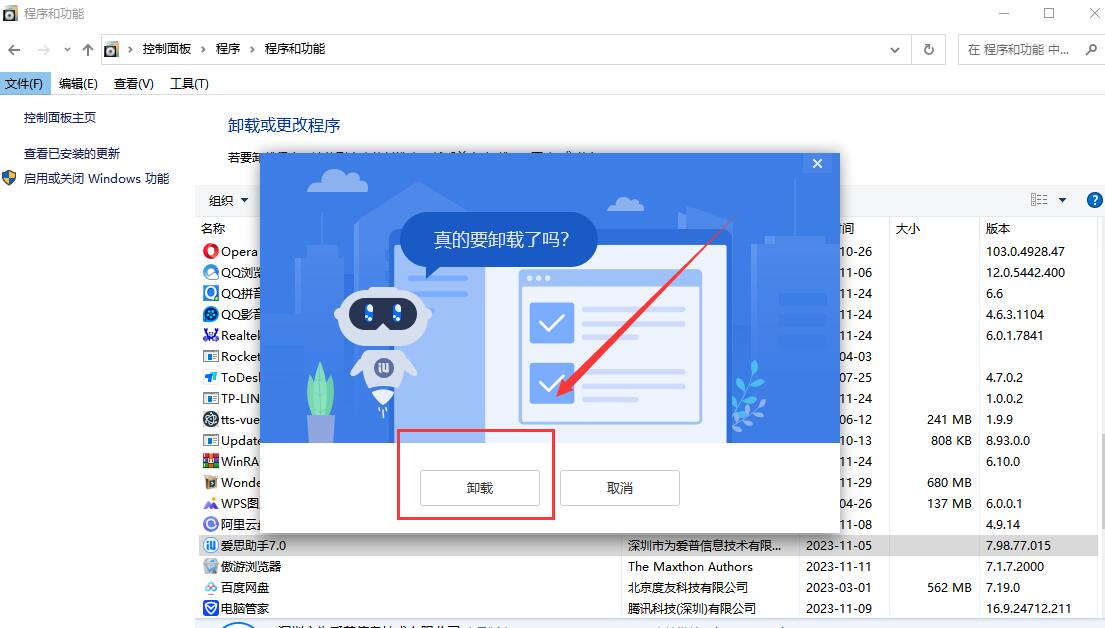
计算机找不到msvcp120.dll如何解决?总结五个可靠的教程
在计算机使用过程中,遇到“找不到msvcp120.dll”这一问题常常令人困扰。msvcp120.dll作为Windows系统中至关重要的动态链接库文件,对于许多应用程序的正常运行起着不可或缺的作用。那么,究竟是什么原因导致找不到msvcp120.dll呢?又…...

法线变换矩阵的推导
背景 在冯氏光照模型中,其中的漫反射项需要我们对法向量和光线做点乘计算。 从顶点着色器中读入的法向量数据处于模型空间,我们需要将法向量转换到世界空间,然后在世界空间中让法向量和光线做运算。这里便有一个问题,如何将法线…...
React.Children.map 和 js 的 map 有什么区别?
JavaScript 中的 map 不会对为 null 或者 undefined 的数据进行处理,而 React.Children.map 中的 map 可以处理 React.Children 为 null 或者 undefined 的情况。 React 空节点:可以由null、undefined、false、true创建 import React from reactexport …...

13.Kubernetes部署Go应用完整流程:从Dockerfile到Ingress发布完整流程
本文以一个简单的Go应用Demo来演示Kubernetes应用部署的完整流程 1、Dockerfile多阶段构建 Dockerfile多阶段构建 [root@docker github]# git clone https://gitee.com/yxydde/http-dump.git [root@docker github]# cd http-dump/ [root@docker http-dump]# cat Dockerfile …...
叉车车载终端定制_基于MT6762安卓核心板的车载终端设备方案
叉车车载终端是一款专为叉车车载场景设计的4英寸Android车载平板电脑。它采用了高能低耗的8核ARM架构处理器和交互开放的Android 12操作系统,算力表现强大。此外,该产品还具备丰富的Wi-Fi-5、4G LTE和蓝牙等通讯功能,可选配外部车载蘑菇天线&…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
