法线变换矩阵的推导
背景
在冯氏光照模型中,其中的漫反射项需要我们对法向量和光线做点乘计算。
从顶点着色器中读入的法向量数据处于模型空间,我们需要将法向量转换到世界空间,然后在世界空间中让法向量和光线做运算。这里便有一个问题,如何将法线从当前的模型空间变换到世界空间?
首先,法向量只是一个方向向量,不能表达空间中的特定位置。同时,法向量没有齐次坐标(顶点位置中的w分量)。这意味着,位移不应该影响到法向量。因此,如果我们打算把法向量乘以一个模型矩阵,我们就要从矩阵中移除位移部分,只选用模型矩阵左上角3×3的矩阵(注意,我们也可以把法向量的w分量设置为0,再乘以4×4矩阵;这同样可以移除位移)。对于法向量,我们只希望对它实施缩放和旋转变换。
其次,如果模型矩阵执行了不等比缩放,顶点的改变会导致法向量不再垂直于表面了。因此,我们不能用这样的模型矩阵来变换法向量。下面的图展示了应用了不等比缩放的模型矩阵对法向量的影响:

当我们应用一个不等比缩放时(注意:等比缩放不会破坏法线,因为法线的方向没被改变,仅仅改变了法线的长度,而这很容易通过标准化来修复),法向量就不会再垂直于对应的表面了,这样光照就会被破坏。
修复这个行为的诀窍是使用一个为法向量专门定制的模型矩阵。这个矩阵称之为法线矩阵(Normal Matrix),它使用了一些线性代数的操作来移除对法向量错误缩放的影响。
推导过程
为了将一个顶点从模型空间转换到世界空间,我们可以乘上一个模型矩阵model,包含物体的移动、旋转、缩放信息。在shader中的代码如下:
FragPos = vec3(model * vec4(aPos, 1.0));
对于一个向量,正如上面的图展示的一样,我们不能简单乘上model矩阵。如果乘上model矩阵,向量就不再和原来的表面切线垂直了。
我们可以定义表面切线为 T = P 2 − P 1 T = P_2 - P1 T=P2−P1,其中 P 1 , P 2 P_1,P_2 P1,P2都是表面上的顶点。当表面前线乘上model矩阵时,我们有:
m o d e l ∗ T = m o d e l ∗ P 2 − m o d e l ∗ P 1 T ′ = P 2 ′ − P 1 ′ model * T = model * P_2 - model * P_1 \\ T' = P_2' - P_1' model∗T=model∗P2−model∗P1T′=P2′−P1′
变换后的表面切线 T ′ T' T′仍然可以表示成表面上顶点的差,因此乘上model矩阵之后,表面切线不会被破坏。
对于表面上的法线 N N N,我们无法从表面上找到两个顶点来表示,但是我们知道表面法线与切线互相垂直,即
N ⋅ T = 0 N \cdot T = 0 N⋅T=0
我们假设矩阵 G G G就是可以将法线从模型空间转换到世界空间的正确矩阵,并用 M M M来表示模型矩阵model,于是有下式:
N ′ ⋅ T ′ = ( G N ) ⋅ ( M T ) = 0 N' \cdot T' = (GN)\cdot(MT) = 0 N′⋅T′=(GN)⋅(MT)=0
转化成矩阵表示的形式
( G N ) ⋅ ( M T ) = ( G N ) T ∗ ( M T ) = N T G T M T = 0 (GN)\cdot(MT) = (GN)^T*(MT) = N^TG^TMT = 0 (GN)⋅(MT)=(GN)T∗(MT)=NTGTMT=0
我们知道 N ⋅ T = N T T = 0 N\cdot T = N^TT = 0 N⋅T=NTT=0,所以如果 G T M = a I G^TM = aI GTM=aI, a a a是任意非零常数,我们便有
N ′ ⋅ T ′ = N T G T M T = N T a I T = a N T T = 0 N'\cdot T' = N^TG^TMT = N^TaIT = aN^TT = 0 N′⋅T′=NTGTMT=NTaIT=aNTT=0
由于我们不想改变法向量的模长,因此令 a = 1 a = 1 a=1,只要满足 G T M = I G^TM = I GTM=I的条件,我们就可以说 G G G是我们最终需要的矩阵,进一步计算
G T M = I ⟷ G = ( M − 1 ) T G^TM = I \longleftrightarrow G = (M^{-1})^T GTM=I⟷G=(M−1)T
最终可得,将法线从模型空间转换到世界空间的矩阵为 ( M − 1 ) T (M^{-1})^T (M−1)T。
补充说明
当模型矩阵只进行了旋转或等比缩放时,我们用这个矩阵来变换法线向量,可以得到正确的结果。
这是因为旋转矩阵和等比缩放矩阵都是正交矩阵,正交矩阵有一个属性:矩阵的转置等于矩阵的逆。
因此
M − 1 = M T → G = ( M − 1 ) T = M M^{-1} = M^T \rightarrow G = (M^{-1})^T = M M−1=MT→G=(M−1)T=M
参考
https://learnopengl-cn.github.io/02%20Lighting/02%20Basic%20Lighting/
http://www.lighthouse3d.com/tutorials/glsl-12-tutorial/the-normal-matrix/
相关文章:

法线变换矩阵的推导
背景 在冯氏光照模型中,其中的漫反射项需要我们对法向量和光线做点乘计算。 从顶点着色器中读入的法向量数据处于模型空间,我们需要将法向量转换到世界空间,然后在世界空间中让法向量和光线做运算。这里便有一个问题,如何将法线…...
React.Children.map 和 js 的 map 有什么区别?
JavaScript 中的 map 不会对为 null 或者 undefined 的数据进行处理,而 React.Children.map 中的 map 可以处理 React.Children 为 null 或者 undefined 的情况。 React 空节点:可以由null、undefined、false、true创建 import React from reactexport …...

13.Kubernetes部署Go应用完整流程:从Dockerfile到Ingress发布完整流程
本文以一个简单的Go应用Demo来演示Kubernetes应用部署的完整流程 1、Dockerfile多阶段构建 Dockerfile多阶段构建 [root@docker github]# git clone https://gitee.com/yxydde/http-dump.git [root@docker github]# cd http-dump/ [root@docker http-dump]# cat Dockerfile …...
叉车车载终端定制_基于MT6762安卓核心板的车载终端设备方案
叉车车载终端是一款专为叉车车载场景设计的4英寸Android车载平板电脑。它采用了高能低耗的8核ARM架构处理器和交互开放的Android 12操作系统,算力表现强大。此外,该产品还具备丰富的Wi-Fi-5、4G LTE和蓝牙等通讯功能,可选配外部车载蘑菇天线&…...
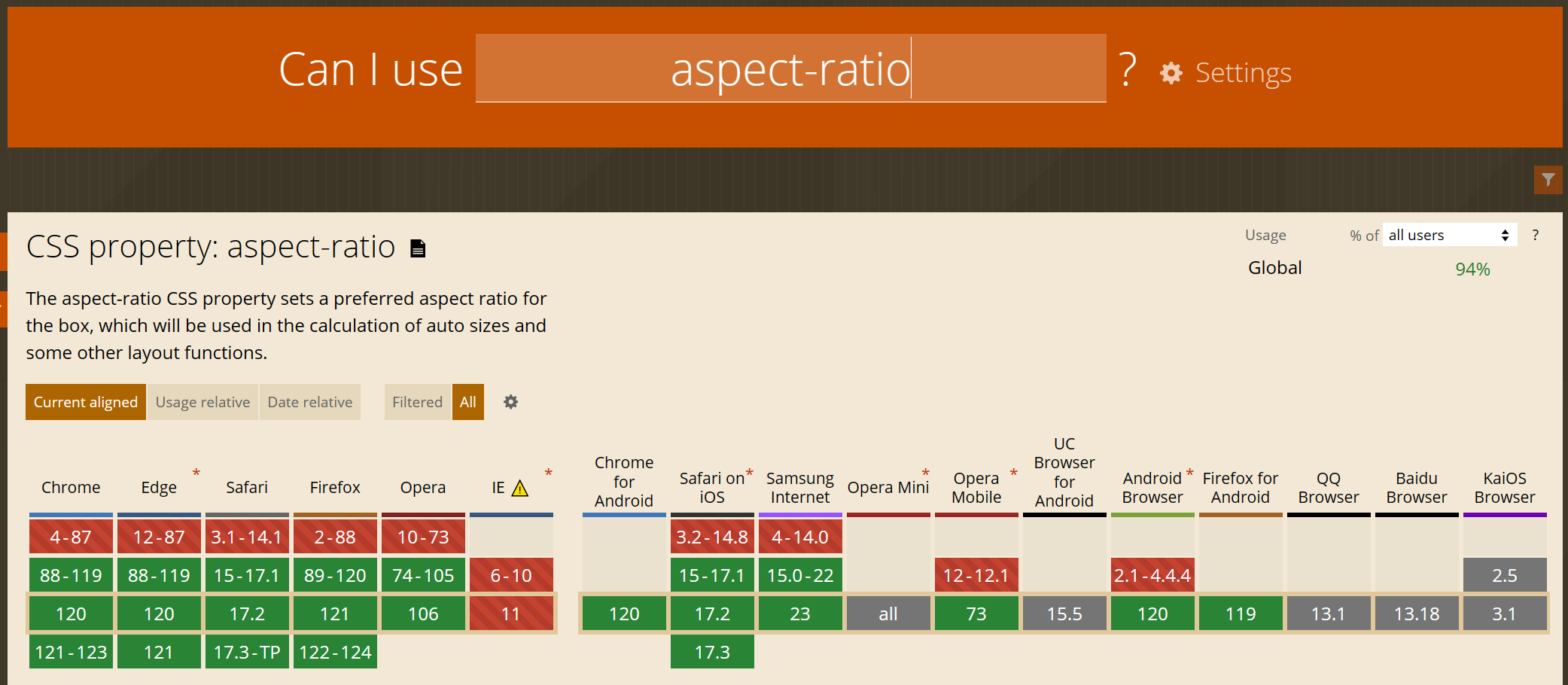
【CSS】保持元素宽高比
保持元素的宽高比,在视频或图片展示类页面是一个重要功能。 本文介绍其常规的实现方法。 实现效果 当浏览器视口发生变化时,元素的尺寸随之变化,且宽高比不变。 代码实现 我们用最简单的元素结构来演示,实现宽高比为4…...

使用 Docker 和 Diffusers 快速上手 Stable Video Diffusion 图生视频大模型
本篇文章聊聊,如何快速上手 Stable Video Diffusion (SVD) 图生视频大模型。 写在前面 月底计划在机器之心的“AI技术论坛”做关于使用开源模型 “Stable Diffusion 模型” 做有趣视频的实战分享。 因为会议分享时间有限,和之前一样,比较简…...

C++ namespace高级用法
高级用法 C++中的命名空间(namespace)是一种用于组织代码的机制,它可以帮助避免命名冲突,并使代码更加清晰和易于维护。以下是C++命名空间的一些高级用法: 嵌套命名空间:命名空间可以嵌套在其他命名空间中,形成一个层次结构。嵌套命名空间可以进一步细化命名空间,使其更…...

如何允许远程访问 MySQL
前些天发现了一个人工智能学习网站,通俗易懂,风趣幽默,最重要的屌图甚多,忍不住分享一下给大家。点击跳转到网站。 如何允许远程访问 MySQL 现在许多网站和应用程序一开始的 Web 服务器和数据库后端都托管在同一台计算机上。随着…...

PostgreSQL认证考试PGCA、PGCE、PGCM
PostgreSQL认证考试PGCA、PGCE、PGCM 【重点!重点!重点!】PGCA、PGCE、PGCM 直通车快速下正,省心省力,每2个月一次考试 PGCE考试通知 (2024) 一、考试概览 (一) 报名要…...
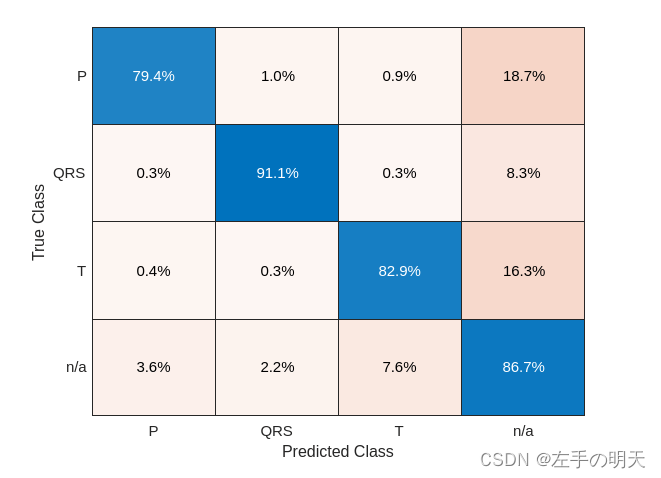
Matlab深度学习进行波形分割(二)
🔗 运行环境:Matlab 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 🔐#### 防伪水印——左手の明天 ####🔐 💗 大家…...

Markdown高级用法——mermaid
Markdown高级用法——mermaid 起初是写文章,其中有时序图流程图等一般是processOn或者draw.io画截图粘过去的,工作中又是腾讯文档,上面也能画图,但假如我笔记软件用语雀之类的又要把一张图反复粘贴,浪费内存ÿ…...

cf919Div2C题题目总结
Problem - C - Codeforces 这道题其实是一道数学题。 先看第一个变量,也就是我们要求的答案k的数量,但看k是很好确定它的限制条件的,要想均匀分成k份,n%k必须为0,有了k,我们再来看m,对于a(1)和…...

Pandas实战100例 | 案例 4: 数据选择和索引 - 选择特定的列和行
案例 4: 数据选择和索引 - 选择特定的列和行 知识点讲解 在 Pandas 中,选择数据是一个非常常见的操作。你可以选择特定的列或行,或者基于某些条件筛选数据。 示例代码 选择特定的列 # 选择单列 selected_column df[ColumnName]# 选择多列 selected…...

Netty-Netty实现自己的通信框架
通信框架功能设计 功能描述 通信框架承载了业务内部各模块之间的消息交互和服务调用,它的主要功能如下: 基于 Netty 的 NIO 通信框架,提供高性能的异步通信能力; 提供消息的编解码框架,可以实现 POJO 的序列化和反…...

【算法刷题】总结规律 算法题目第2讲 [234] 回文链表,因为深浅拷贝引出的bug
配合b站视频讲解食用更佳:https://www.bilibili.com/video/BV1vW4y1P7V7 核心提示:好几道题是处理有序数组的! 适合人群:考研/复试/面试 解决痛点:1. 刷了就忘 2.换一道相似的题就不会 学完后会输出:对每类题目的框架…...

RabbitMQ如何保证消息不丢失?
RabbitMQ如何保证消息不丢失? 消息丢失的情况 生产者发送消息未到达交换机生产者发送消息未到达队列MQ宕机,消息丢失消费者服务宕机,消息丢失 生产者确认机制 解决的问题:publisher confirm机制来避免消息发送到MQ过程中消失。…...
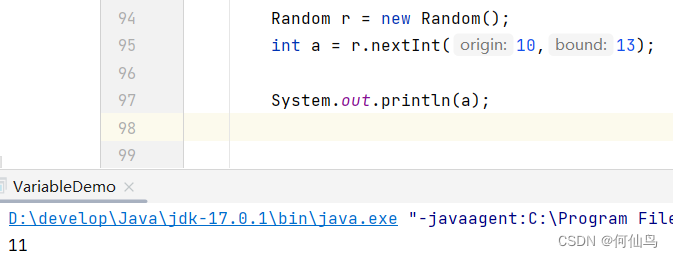
Random的使用
作用:生成伪随机数 1.导包:import java.util.Random 2.得到随机数对象:Random r new Random(); 3.调用随机数的功能获取随机数: 这里随机生成一个0-9的整数: int number r.nextInt(10); 实现指定区间的随机数&a…...
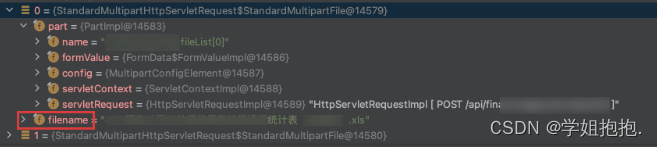
通过反射修改MultipartFile类文件名
1、背景 项目上有这样一个需求,前端传文件过来,后端接收后按照特定格式对文件进行重命名。(修改文件名需求其实也可以在前端处理的) //接口类似于下面这个样子 PosMapping("/uploadFile") public R uploadFile(List<MultipartFile> fil…...
Macos下修改Python版本
MacOS下修改Python版本 安装 查看本机已安装的Python版本:where python3 ~ where python3 /usr/bin/python3 /usr/local/bin/python3 /Library/Frameworks/Python.framework/Versions/3.12/bin/python3如果没有你想要的版本,去python官网下载安装包。…...

多种采购方式下,数智化招标采购系统建设解决方案
广发证券成立于1991年,是国内首批综合类证券公司,先后于2010年和2015年在深圳证券交易所及香港联合交易所主板上市。 多年来,广发证券在竞争激烈、复杂多变的行业环境中努力开拓、锐意进取,以卓越的经营业绩、持续完善的全面风险…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
