当前位置： 首页 > news >正文

RabbitMQ如何保证消息不丢失？

news 2025/10/22 7:56:05
RabbitMQ如何保证消息不丢失？

消息丢失的情况

  1. 生产者发送消息未到达交换机
  2. 生产者发送消息未到达队列
  3. MQ宕机，消息丢失
  4. 消费者服务宕机，消息丢失
生产者确认机制

解决的问题：publisher confirm机制来避免消息发送到MQ过程中消失。

当消息成功发送到MQ：会返回一个publish-confirm ack(acknowledge)

消息发送到交换机失败： publish-confirm nack

消息路由到队列失败：publish-return ack

消息失败后如何处理？

    1. 回调方法即时重发（再发一次）
    2. 记录日志（如果重发后还是失败可以记录到日志中）
    3. 保存到数据库然后定时重发，成功发送后即可删除表中的数据（再失败的话，人工解决）
持久化

保证保存在MQ中的消息不丢失。

MQ默认是内存存储消息，开启持久化功能可以确保缓存在MQ中的消息不丢失。

交换机持久化，队列持久化，消息持久化

消费者确认

处理问题：消费者导致的消息丢失问题。

消费者确认机制：消费者处理消息后可以向MQ发送ack回执，MQ收到ack回执后才会删除该消息。

SpringAMQP可以配置的三种确认模式：

manual: 手动ack

auto:自动ack。Spring检测listener代码是否异常。

none: 关闭ack，MQ假定消费者获取消息后会成功处理，因此消息投递后立即被删除。

相关文章：

RabbitMQ如何保证消息不丢失？

RabbitMQ如何保证消息不丢失？ 消息丢失的情况 生产者发送消息未到达交换机生产者发送消息未到达队列MQ宕机，消息丢失消费者服务宕机，消息丢失 生产者确认机制 解决的问题：publisher confirm机制来避免消息发送到MQ过程中消失。…...

编程日记 2024/1/15 0:40:03

Random的使用

作用：生成伪随机数 1.导包：import java.util.Random 2.得到随机数对象：Random r new Random(); 3.调用随机数的功能获取随机数： 这里随机生成一个0-9的整数： int number r.nextInt(10); 实现指定区间的随机数&a…...

编程日记 2024/1/15 0:37:01

通过反射修改MultipartFile类文件名

1、背景 项目上有这样一个需求&#xff0c;前端传文件过来&#xff0c;后端接收后按照特定格式对文件进行重命名。(修改文件名需求其实也可以在前端处理的) //接口类似于下面这个样子 PosMapping("/uploadFile") public R uploadFile(List<MultipartFile> fil…...

编程日记 2024/1/15 0:34:57

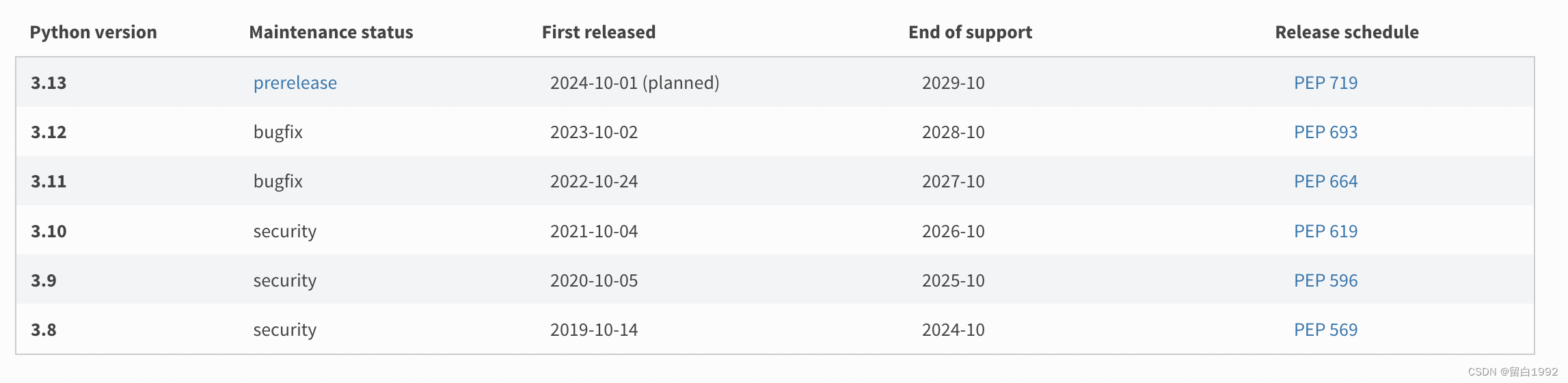
Macos下修改Python版本

MacOS下修改Python版本 安装 查看本机已安装的Python版本&#xff1a;where python3 ~ where python3 /usr/bin/python3 /usr/local/bin/python3 /Library/Frameworks/Python.framework/Versions/3.12/bin/python3如果没有你想要的版本&#xff0c;去python官网下载安装包。…...

编程日记 2024/1/15 0:32:55

多种采购方式下，数智化招标采购系统建设解决方案

广发证券成立于1991年&#xff0c;是国内首批综合类证券公司&#xff0c;先后于2010年和2015年在深圳证券交易所及香港联合交易所主板上市。 多年来&#xff0c;广发证券在竞争激烈、复杂多变的行业环境中努力开拓、锐意进取&#xff0c;以卓越的经营业绩、持续完善的全面风险…...

编程日记 2024/1/15 0:31:54

Java选择排序

选择排序是一种简单直观的排序算法&#xff0c;其基本思想是每一轮从待排序的元素中选择最小&#xff08;或最大&#xff09;的元素&#xff0c;将其与当前位置的元素交换。选择排序的实现步骤可以简要概括为&#xff1a; 初始化&#xff1a; 遍历整个数组&#xff0c;将当前位…...

编程日记 2024/1/15 0:30:53

[足式机器人]Part3 机构运动学与动力学分析与建模 Ch00-1 坐标系与概念基准

本文仅供学习使用&#xff0c;总结很多本现有讲述运动学或动力学书籍后的总结&#xff0c;从矢量的角度进行分析&#xff0c;方法比较传统&#xff0c;但更易理解&#xff0c;并且现有的看似抽象方法&#xff0c;两者本质上并无不同。 2024年底本人学位论文发表后方可摘抄 若有…...

编程日记 2024/1/15 0:26:49

【金猿人物展】DataPipelineCEO陈诚：赋能数据应用，发挥未来生产力

‍ 陈诚 本文由DataPipelineCEO陈诚撰写并投递参与“数据猿年度金猿策划活动——2023大数据产业年度趋势人物榜单及奖项”评选。 大数据产业创新服务媒体 ——聚焦数据 改变商业 我们处在一个“见证奇迹”的时代。在过去的20年间&#xff0c;我们见证了大数据技术快速发展所带…...

编程日记 2024/1/15 0:25:48

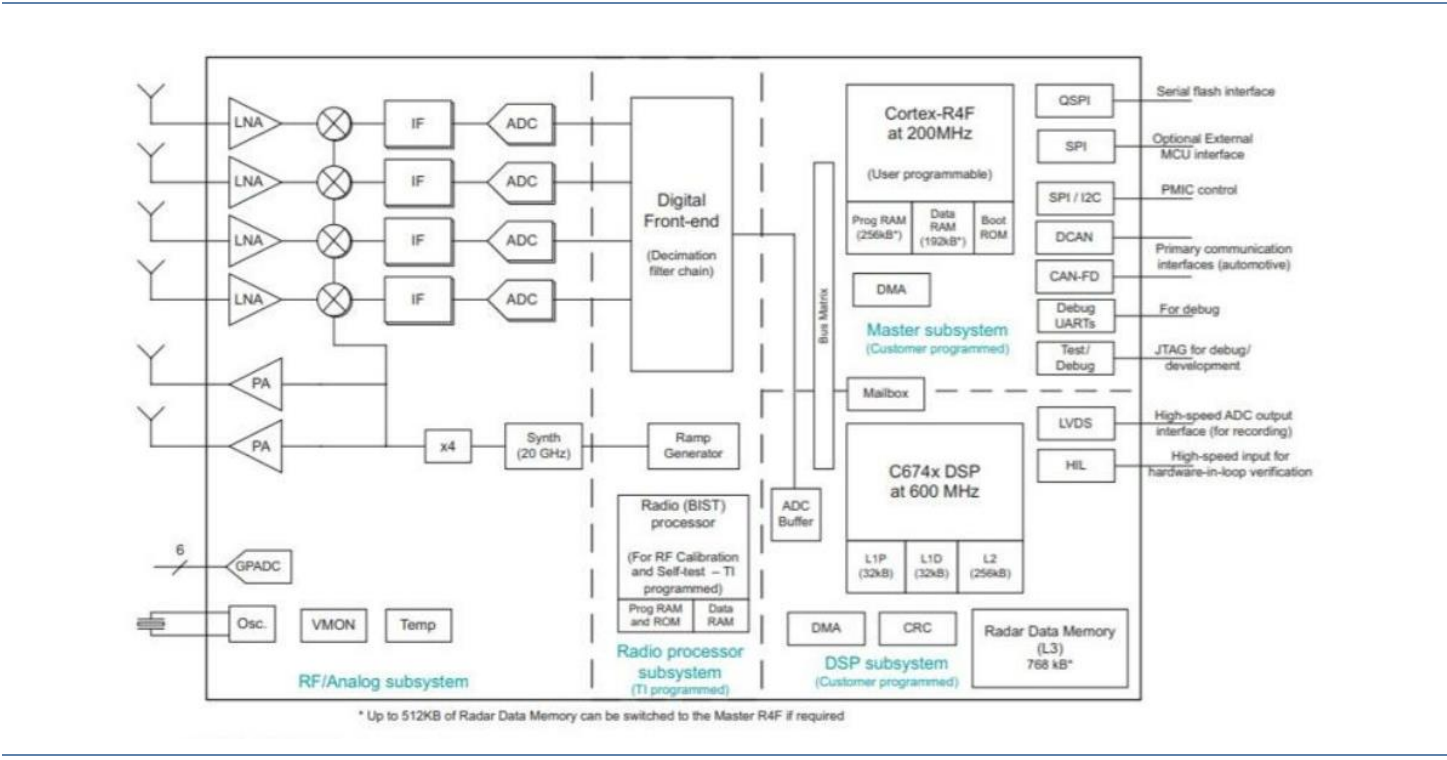
4D 毫米波雷达：智驾普及的新路径（二）

4 4D 毫米波的技术路线探讨 4.1 前端收发模块 MMIC&#xff1a;级联、CMOS、AiP 4.1.1 设计&#xff1a;级联、单芯片、虚拟孔径 4D 毫米波雷达的技术路线主要分为三种&#xff0c;分别是多级联、级联 虚拟孔径成像技术、以及 集成芯片。&#xff08; 1 &#xff09;多级…...

编程日记 2024/1/15 0:24:47

element plus自定义组件表单校验

方式一&#xff1a; import { formContextKey, formItemContextKey } from "element-plus";// 获取 el-form 组件上下文 const formContext inject(formContextKey, void 0); // 获取 el-form-item 组件上下文 const formItemContext inject(formItemContextKey, …...

编程日记 2024/1/15 0:22:46

C //练习 4-13 编写一个递归版本的reverse(s)函数，以将字符串s倒置。

C程序设计语言 &#xff08;第二版&#xff09; 练习 4-13 练习 4-13 编写一个递归版本的reverse(s)函数&#xff0c;以将字符串s倒置。 注意&#xff1a;代码在win32控制台运行&#xff0c;在不同的IDE环境下&#xff0c;有部分可能需要变更。 IDE工具&#xff1a;Visual S…...

编程日记 2024/1/15 0:21:45

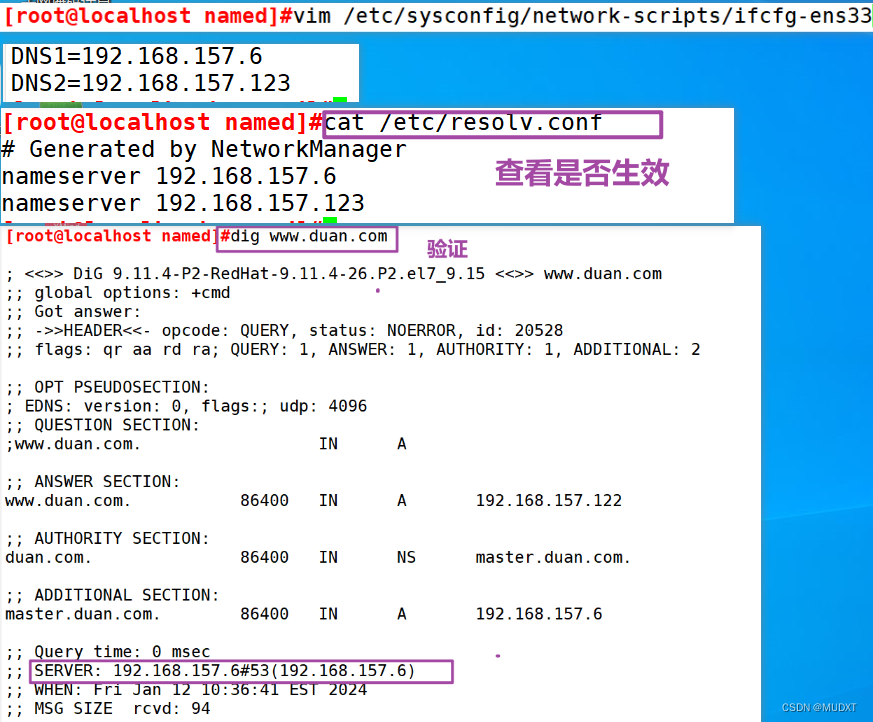
DNS解析和主从复制

一、DNS名称解析协议 二、DNS正向解析 三、DNS主从复制 主服务器 从服务器...

编程日记 2024/1/15 0:19:41

光猫（无限路由器）插入可移动硬盘搭建简易版的NAS

1.场景分析 最近查询到了许多有关NAS的资料&#xff0c;用来替代百度云盘等确实有很多优势&#xff0c;尤其是具有不限速&#xff08;速度看自己配置&#xff09;、私密性好、一次投入后续只需要电费即可等优势。鉴于手上没有可以用的资源-cpu、机箱、内存等&#xff0c;查询到…...

编程日记 2024/1/15 0:17:39

SpringIOC之support模块GenericGroovyApplicationContext

博主介绍&#xff1a;✌全网粉丝5W&#xff0c;全栈开发工程师&#xff0c;从事多年软件开发&#xff0c;在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战&#xff0c;博主也曾写过优秀论文&#xff0c;查重率极低&#xff0c;在这方面有丰富的经验…...

编程日记 2024/1/15 0:16:38

Awesome 3D Gaussian Splatting Resources

GitHub - MrNeRF/awesome-3D-gaussian-splatting: Curated list of papers and resources focused on 3D Gaussian Splatting, intended to keep pace with the anticipated surge of research in the coming months. 3D Gaussian Splatting简明教程 - 知乎...

编程日记 2024/1/15 0:15:37

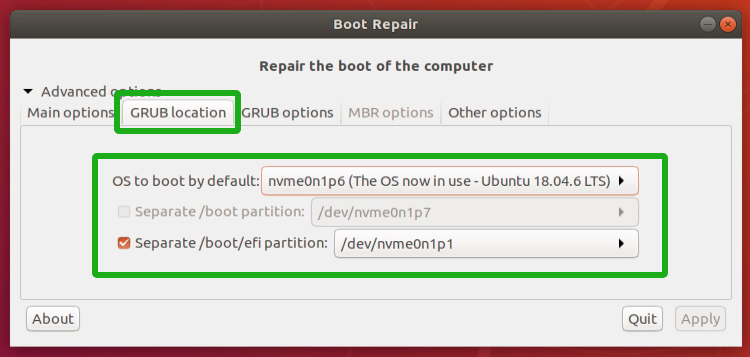
【镜像压缩】linux 上 SD/TF 卡镜像文件压缩到实际大小的简单方法（树莓派、nvidia jetson）

文章目录 1. 备份 SD/TF 卡为镜像文件2. 压缩镜像文件2.1. 多分区镜像文件的压缩&#xff08;树莓派、普通 linux 系统等&#xff09;2.2. 单分区镜像文件的压缩&#xff08;Nvidia Jetson Nano 等&#xff09; 3. 还原镜像文件到 SD/TF 卡4. 镜像还原后处理4.1. 镜像分区调整4…...

编程日记 2024/1/15 0:13:36

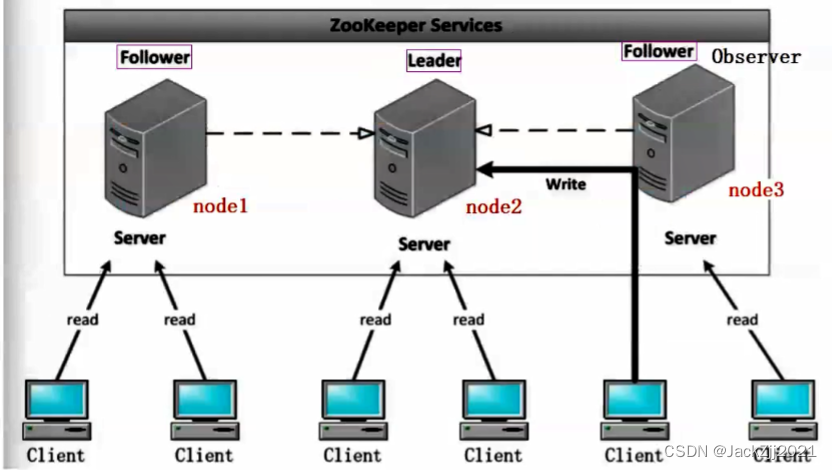
Zookeeper 和 naocs的区别

Nacos 和 ZooKeeper 都是服务发现和配置管理的工具&#xff0c;它们的主要区别如下&#xff1a;功能特性&#xff1a;Nacos 比 ZooKeeper 更加强大&#xff0c;Nacos 支持服务发现、动态配置、流量管理、服务治理、分布式事务等功能&#xff0c;而 ZooKeeper 主要用于分布式协调…...

编程日记 2024/1/15 0:10:33

2-6基础算法-快速幂/倍增/构造

文章目录 一.快速幂二.倍增三.构造 一.快速幂 快速幂算法是一种高效计算幂ab的方法&#xff0c;特别是当b非常大时。它基于幂运算的性质&#xff0c;将幂运算分解成一系列的平方操作&#xff0c;以此减少乘法的次数。算法的核心在于将指数b表示为二进制形式&#xff0c;并利用…...

编程日记 2024/1/15 0:08:31

行业内参～移动广告行业大盘趋势-2023年12月

前言 2024年&#xff0c;移动广告的钱越来越难赚了。市场竞争激烈到前所未有的程度&#xff0c;小型企业和独立开发者在巨头的阴影下苦苦挣扎。随着广告成本的上升和点击率的下降&#xff0c;许多原本依赖广告收入的创业者和自由职业者开始感受到前所未有的压力。 &#x1f3…...

编程日记 2024/1/15 0:07:30

【笔记】书生·浦语大模型实战营——第四课（XTuner 大模型单卡低成本微调实战）

【参考&#xff1a;tutorial/xtuner/README.md at main InternLM/tutorial】 【参考&#xff1a;(4)XTuner 大模型单卡低成本微调实战_哔哩哔哩_bilibili-【OpenMMLab】】 总结 学到了 linux系统中 tmux 的使用 了解了 XTuner 大模型微调框架的使用 pth格式参数转Hugging …...

编程日记 2024/1/15 0:06:29

TDengine 快速体验（Docker 镜像方式）

简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能&#xff0c;本节首先介绍如何通过 Docker 快速体验 TDengine&#xff0c;然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker&#xff0c;请使用 安装包的方式快…...

编程新知 2025/10/11 22:38:21

DeepSeek 赋能智慧能源：微电网优化调度的智能革新路径

目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

编程新知 2025/6/15 19:07:20

Python：操作 Excel 折叠

💖亲爱的技术爱好者们，热烈欢迎来到 Kant2048 的博客！我是 Thomas Kant，很开心能在CSDN上与你们相遇～💖 本博客的精华专栏： 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

编程新知 2025/10/20 3:38:39

可靠性+灵活性：电力载波技术在楼宇自控中的核心价值

可靠性灵活性&#xff1a;电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中&#xff0c;电力载波技术&#xff08;PLC&#xff09;凭借其独特的优势&#xff0c;正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据&#xff0c;无需额外布…...

编程新知 2025/9/27 2:43:26

UE5 学习系列（三）创建和移动物体

这篇博客是该系列的第三篇&#xff0c;是在之前两篇博客的基础上展开&#xff0c;主要介绍如何在操作界面中创建和拖动物体&#xff0c;这篇博客跟随的视频链接如下&#xff1a; B 站视频&#xff1a;s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

编程新知 2025/10/19 17:23:52

Keil 中设置 STM32 Flash 和 RAM 地址详解

文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面（Target 选项卡）1. IROM1（用于配置 Flash）2. IRAM1（用于配置 RAM）二、链接器设置界面（Linker 选项卡）1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数（如果没有勾选上面…...

编程新知 2025/10/21 9:22:25

css的定位（position）详解：相对定位 绝对定位 固定定位

在 CSS 中&#xff0c;元素的定位通过 position 属性控制&#xff0c;共有 5 种定位模式&#xff1a;static&#xff08;静态定位&#xff09;、relative&#xff08;相对定位&#xff09;、absolute&#xff08;绝对定位&#xff09;、fixed&#xff08;固定定位&#xff09;和…...

编程新知 2025/8/9 2:28:15

【HarmonyOS 5 开发速记】如何获取用户信息（头像/昵称/手机号）

1.获取 authorizationCode&#xff1a; 2.利用 authorizationCode 获取 accessToken&#xff1a;文档中心 3.获取手机&#xff1a;文档中心 4.获取昵称头像&#xff1a;文档中心 首先创建 request 若要获取手机号&#xff0c;scope必填 phone&#xff0c;permissions 必填 …...

编程新知 2025/9/17 2:39:21

Rapidio门铃消息FIFO溢出机制

关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系&#xff0c;以下是深入解析&#xff1a; 门铃FIFO溢出的本质 在RapidIO系统中&#xff0c;门铃消息FIFO是硬件控制器内部的缓冲区&#xff0c;用于临时存储接收到的门铃消息&#xff08;Doorbell Message&#xff09;。…...

编程新知 2025/9/12 21:09:32

rnn判断string中第一次出现a的下标

# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

编程新知 2025/9/24 16:25:00