Random的使用
作用：生成伪随机数
1.导包：import java.util.Random
2.得到随机数对象：Random r = new Random();
3.调用随机数的功能获取随机数：
这里随机生成一个0-9的整数：
int number = r.nextInt(10);
实现指定区间的随机数：
可以在原基础上加减1个数：int number = r.nextInt(10) + n ;
或者如此：
或者直接给定2个值
相关文章：
Random的使用
作用：生成伪随机数 1.导包：import java.util.Random 2.得到随机数对象：Random r new Random(); 3.调用随机数的功能获取随机数： 这里随机生成一个0-9的整数： int number r.nextInt(10); 实现指定区间的随机数&a…...
通过反射修改MultipartFile类文件名
1、背景 项目上有这样一个需求，前端传文件过来，后端接收后按照特定格式对文件进行重命名。(修改文件名需求其实也可以在前端处理的) //接口类似于下面这个样子 PosMapping("/uploadFile") public R uploadFile(List<MultipartFile> fil…...
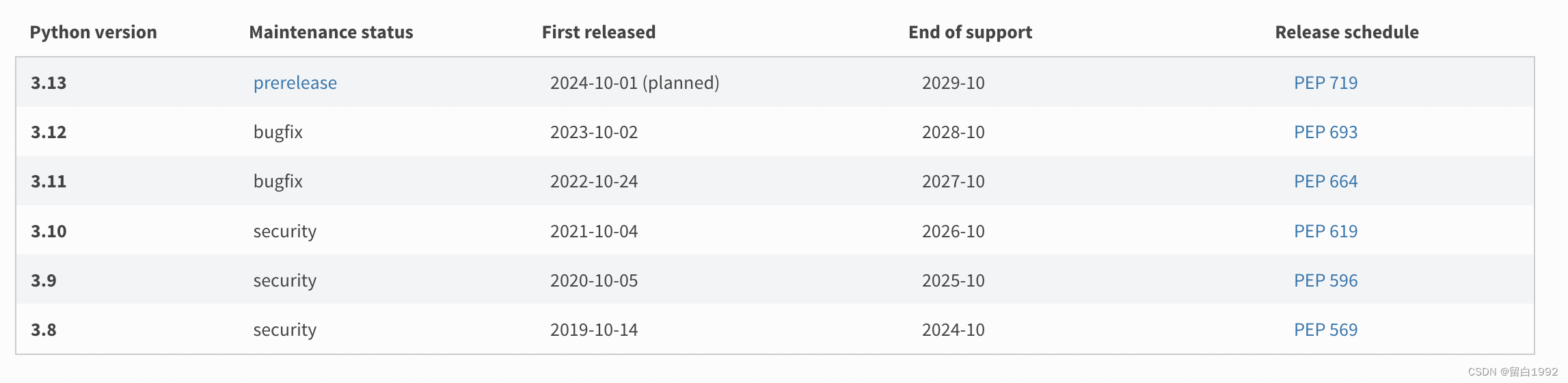
Macos下修改Python版本
MacOS下修改Python版本 安装 查看本机已安装的Python版本：where python3 ~ where python3 /usr/bin/python3 /usr/local/bin/python3 /Library/Frameworks/Python.framework/Versions/3.12/bin/python3如果没有你想要的版本，去python官网下载安装包。…...
多种采购方式下，数智化招标采购系统建设解决方案
广发证券成立于1991年，是国内首批综合类证券公司，先后于2010年和2015年在深圳证券交易所及香港联合交易所主板上市。 多年来，广发证券在竞争激烈、复杂多变的行业环境中努力开拓、锐意进取，以卓越的经营业绩、持续完善的全面风险…...
Java选择排序
选择排序是一种简单直观的排序算法，其基本思想是每一轮从待排序的元素中选择最小（或最大）的元素，将其与当前位置的元素交换。选择排序的实现步骤可以简要概括为： 初始化： 遍历整个数组，将当前位…...
[足式机器人]Part3 机构运动学与动力学分析与建模 Ch00-1 坐标系与概念基准
本文仅供学习使用，总结很多本现有讲述运动学或动力学书籍后的总结，从矢量的角度进行分析，方法比较传统，但更易理解，并且现有的看似抽象方法，两者本质上并无不同。 2024年底本人学位论文发表后方可摘抄 若有…...
【金猿人物展】DataPipelineCEO陈诚：赋能数据应用，发挥未来生产力
陈诚 本文由DataPipelineCEO陈诚撰写并投递参与“数据猿年度金猿策划活动——2023大数据产业年度趋势人物榜单及奖项”评选。 大数据产业创新服务媒体 ——聚焦数据 改变商业 我们处在一个“见证奇迹”的时代。在过去的20年间，我们见证了大数据技术快速发展所带…...
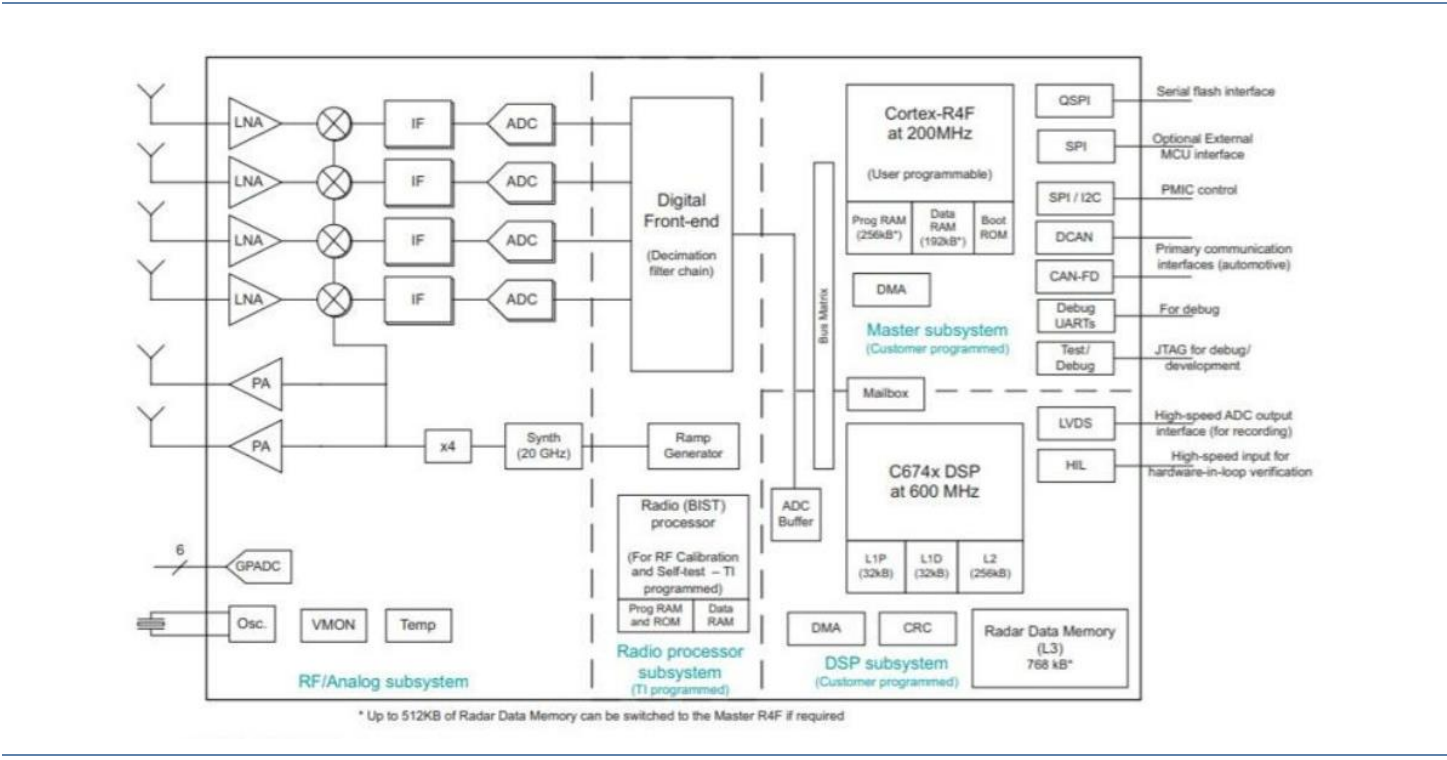
4D 毫米波雷达：智驾普及的新路径（二）
4 4D 毫米波的技术路线探讨 4.1 前端收发模块 MMIC：级联、CMOS、AiP 4.1.1 设计：级联、单芯片、虚拟孔径 4D 毫米波雷达的技术路线主要分为三种，分别是多级联、级联 虚拟孔径成像技术、以及 集成芯片。（ 1 ）多级…...
element plus自定义组件表单校验
方式一： import { formContextKey, formItemContextKey } from "element-plus";// 获取 el-form 组件上下文 const formContext inject(formContextKey, void 0); // 获取 el-form-item 组件上下文 const formItemContext inject(formItemContextKey, …...
函数，以将字符串s倒置。)
C //练习 4-13 编写一个递归版本的reverse(s)函数，以将字符串s倒置。
C程序设计语言 （第二版） 练习 4-13 练习 4-13 编写一个递归版本的reverse(s)函数，以将字符串s倒置。 注意：代码在win32控制台运行，在不同的IDE环境下，有部分可能需要变更。 IDE工具：Visual S…...
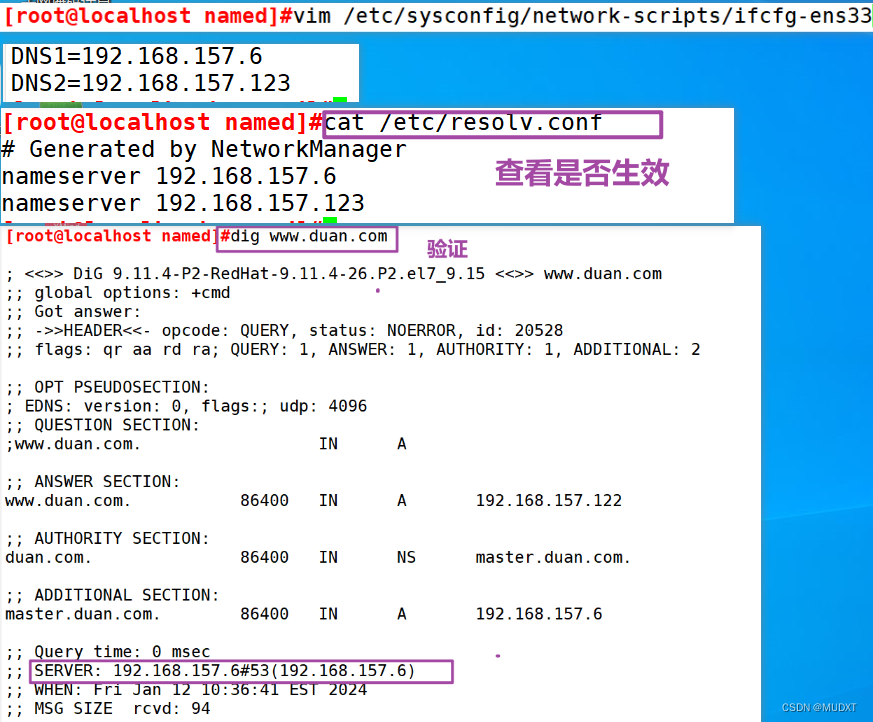
DNS解析和主从复制
一、DNS名称解析协议 二、DNS正向解析 三、DNS主从复制 主服务器 从服务器...
光猫（无限路由器）插入可移动硬盘搭建简易版的NAS
1.场景分析 最近查询到了许多有关NAS的资料，用来替代百度云盘等确实有很多优势，尤其是具有不限速（速度看自己配置）、私密性好、一次投入后续只需要电费即可等优势。鉴于手上没有可以用的资源-cpu、机箱、内存等，查询到…...
SpringIOC之support模块GenericGroovyApplicationContext
博主介绍：✌全网粉丝5W，全栈开发工程师，从事多年软件开发，在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战，博主也曾写过优秀论文，查重率极低，在这方面有丰富的经验…...
Awesome 3D Gaussian Splatting Resources
GitHub - MrNeRF/awesome-3D-gaussian-splatting: Curated list of papers and resources focused on 3D Gaussian Splatting, intended to keep pace with the anticipated surge of research in the coming months. 3D Gaussian Splatting简明教程 - 知乎...
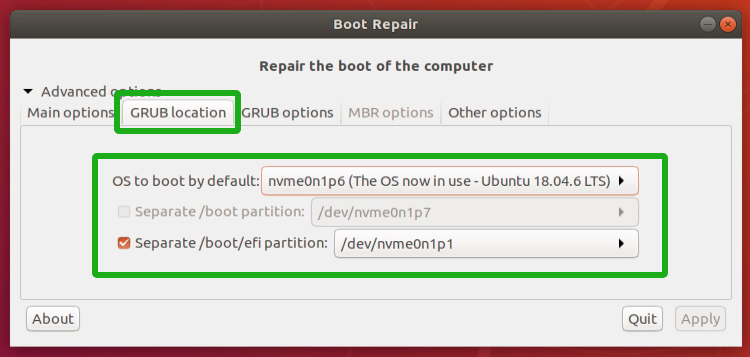
【镜像压缩】linux 上 SD/TF 卡镜像文件压缩到实际大小的简单方法（树莓派、nvidia jetson）
文章目录 1. 备份 SD/TF 卡为镜像文件2. 压缩镜像文件2.1. 多分区镜像文件的压缩（树莓派、普通 linux 系统等）2.2. 单分区镜像文件的压缩（Nvidia Jetson Nano 等） 3. 还原镜像文件到 SD/TF 卡4. 镜像还原后处理4.1. 镜像分区调整4…...
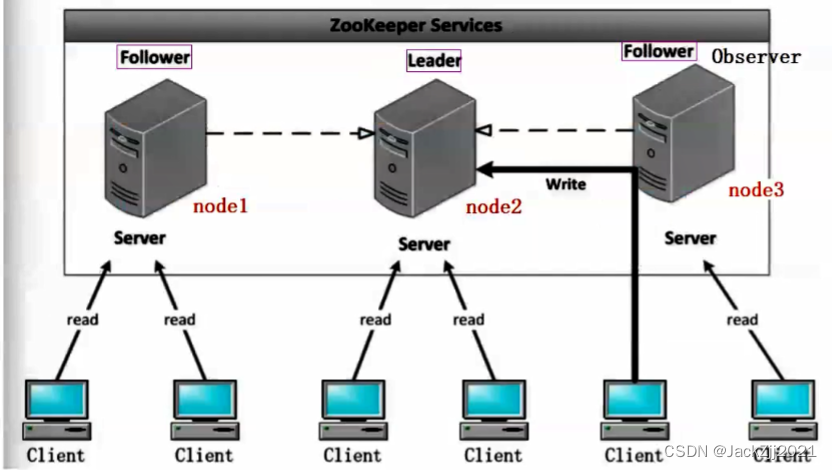
Zookeeper 和 naocs的区别
Nacos 和 ZooKeeper 都是服务发现和配置管理的工具，它们的主要区别如下：功能特性：Nacos 比 ZooKeeper 更加强大，Nacos 支持服务发现、动态配置、流量管理、服务治理、分布式事务等功能，而 ZooKeeper 主要用于分布式协调…...
2-6基础算法-快速幂/倍增/构造
文章目录 一.快速幂二.倍增三.构造 一.快速幂 快速幂算法是一种高效计算幂ab的方法，特别是当b非常大时。它基于幂运算的性质，将幂运算分解成一系列的平方操作，以此减少乘法的次数。算法的核心在于将指数b表示为二进制形式，并利用…...
行业内参～移动广告行业大盘趋势-2023年12月
前言 2024年，移动广告的钱越来越难赚了。市场竞争激烈到前所未有的程度，小型企业和独立开发者在巨头的阴影下苦苦挣扎。随着广告成本的上升和点击率的下降，许多原本依赖广告收入的创业者和自由职业者开始感受到前所未有的压力。 dz…...
【笔记】书生·浦语大模型实战营——第四课（XTuner 大模型单卡低成本微调实战）
【参考：tutorial/xtuner/README.md at main InternLM/tutorial】 【参考：(4)XTuner 大模型单卡低成本微调实战_哔哩哔哩_bilibili-【OpenMMLab】】 总结 学到了 linux系统中 tmux 的使用 了解了 XTuner 大模型微调框架的使用 pth格式参数转Hugging …...
开源的Immich自建一个堪比 iCloud 的私有云相册和备份服务
源码地址 GitHub - immich-app/immich: Self-hosted photo and video backup solution directly from your mobile phone. 1.创建目录 mkdir /data/immich && cd /data/immich 2.下载docker-compose文件和.env文件 wget https://github.com/immich-app/immich/relea…...
: K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？)
云原生核心技术 (7/12): K8s 核心概念白话解读(上)：Pod 和 Deployment 究竟是什么？
大家好，欢迎来到《云原生核心技术》系列的第七篇！ 在上一篇，我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在，我们就像一个拥有了一块崭新数字土地的农场主，是时…...
SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外，K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案，全安装在K8S群集中。 具体可参…...
51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留，CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制（CCA-Attention），…...
脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）
一、数据处理与分析实战 （一）实时滤波与参数调整 基础滤波操作 60Hz 工频滤波：勾选界面右侧 “60Hz” 复选框，可有效抑制电网干扰（适用于北美地区，欧洲用户可调整为 50Hz）。 平滑处理&…...
Python：操作 Excel 折叠
💖亲爱的技术爱好者们，热烈欢迎来到 Kant2048 的博客！我是 Thomas Kant，很开心能在CSDN上与你们相遇～💖 本博客的精华专栏： 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...
Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明：server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...
-----深度优先搜索（DFS）实现)
c++ 面试题(1)-----深度优先搜索（DFS）实现
操作系统：ubuntu22.04 IDE:Visual Studio Code 编程语言：C11 题目描述 地上有一个 m 行 n 列的方格，从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子，但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...
现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学（ECC）是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础，例如椭圆曲线数字签…...
【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类：块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务： test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...