cf919Div2C题题目总结
Problem - C - Codeforces
这道题其实是一道数学题。
先看第一个变量,也就是我们要求的答案k的数量,但看k是很好确定它的限制条件的,要想均匀分成k份,n%k必须为0,有了k,我们再来看m,对于a(1)和a(k+1),要使它们除以m后相同,肯定满足一下式子a(1)=x1*m1+n1,a(k+1)=y1*m1+n1对于其它的对应的a也是一样的,a(2)=x2*m2+n2,a(k+2)=y2*m2+n2……,那么只要知道m1是否等于m2就可以了吧,如果m1等于m2就说明m存在,在有n1和n2的阻碍下,显然算不出m,不妨将两者相减a(1)-a(k+1)=(x1-y1)*m1,a(2)-a(k+2)=(x2-y2)*m2,,这个时候求一个m,不就是求两式的最大公因数吗,为什么是最大公因数,因为题中m有限制m要求大于等于2,它们的公因数可能有很多个,但是大于2的不一定有,所以求一个最大公因数,看看是否大于2。那么解法显而易见了,枚举k,然后求每个子数组对应元素差的最大公因数,看它是否大于等于2,及不等于1,如果是ans++。
using i64 = long long;
i64 gcd(i64 a, i64 b) {while (b) {i64 temp = b;b=a%b;a = temp;}return std::abs(a);
}
void solve() {int n;std::cin >> n;std::vector<int> a(n);for (int i = 0; i < n; i++) {std::cin >> a[i];}int ans = 0;for (int k = 1; k <= n; k++) {if (n % k == 0) {int g = 0;for (int i = k; i < n; i++) {g = gcd(g, a[i] - a[i - k]);}ans += (g != 1);}}std::cout << ans << "\n";
}int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int t;std::cin >> t;while (t--) {solve();}return 0;
}相关文章:

cf919Div2C题题目总结
Problem - C - Codeforces 这道题其实是一道数学题。 先看第一个变量,也就是我们要求的答案k的数量,但看k是很好确定它的限制条件的,要想均匀分成k份,n%k必须为0,有了k,我们再来看m,对于a(1)和…...

Pandas实战100例 | 案例 4: 数据选择和索引 - 选择特定的列和行
案例 4: 数据选择和索引 - 选择特定的列和行 知识点讲解 在 Pandas 中,选择数据是一个非常常见的操作。你可以选择特定的列或行,或者基于某些条件筛选数据。 示例代码 选择特定的列 # 选择单列 selected_column df[ColumnName]# 选择多列 selected…...

Netty-Netty实现自己的通信框架
通信框架功能设计 功能描述 通信框架承载了业务内部各模块之间的消息交互和服务调用,它的主要功能如下: 基于 Netty 的 NIO 通信框架,提供高性能的异步通信能力; 提供消息的编解码框架,可以实现 POJO 的序列化和反…...

【算法刷题】总结规律 算法题目第2讲 [234] 回文链表,因为深浅拷贝引出的bug
配合b站视频讲解食用更佳:https://www.bilibili.com/video/BV1vW4y1P7V7 核心提示:好几道题是处理有序数组的! 适合人群:考研/复试/面试 解决痛点:1. 刷了就忘 2.换一道相似的题就不会 学完后会输出:对每类题目的框架…...

RabbitMQ如何保证消息不丢失?
RabbitMQ如何保证消息不丢失? 消息丢失的情况 生产者发送消息未到达交换机生产者发送消息未到达队列MQ宕机,消息丢失消费者服务宕机,消息丢失 生产者确认机制 解决的问题:publisher confirm机制来避免消息发送到MQ过程中消失。…...
Random的使用
作用:生成伪随机数 1.导包:import java.util.Random 2.得到随机数对象:Random r new Random(); 3.调用随机数的功能获取随机数: 这里随机生成一个0-9的整数: int number r.nextInt(10); 实现指定区间的随机数&a…...
通过反射修改MultipartFile类文件名
1、背景 项目上有这样一个需求,前端传文件过来,后端接收后按照特定格式对文件进行重命名。(修改文件名需求其实也可以在前端处理的) //接口类似于下面这个样子 PosMapping("/uploadFile") public R uploadFile(List<MultipartFile> fil…...
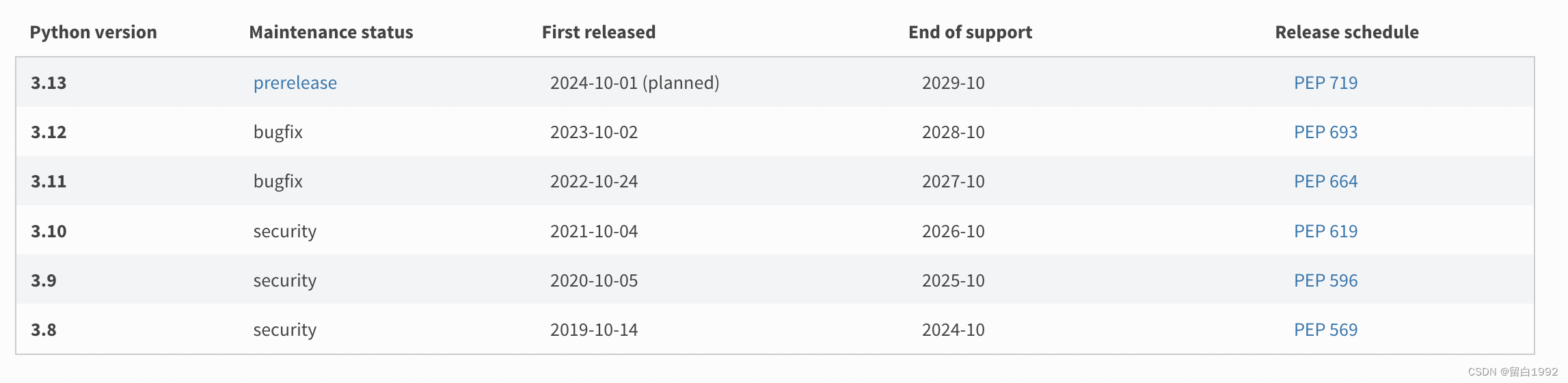
Macos下修改Python版本
MacOS下修改Python版本 安装 查看本机已安装的Python版本:where python3 ~ where python3 /usr/bin/python3 /usr/local/bin/python3 /Library/Frameworks/Python.framework/Versions/3.12/bin/python3如果没有你想要的版本,去python官网下载安装包。…...

多种采购方式下,数智化招标采购系统建设解决方案
广发证券成立于1991年,是国内首批综合类证券公司,先后于2010年和2015年在深圳证券交易所及香港联合交易所主板上市。 多年来,广发证券在竞争激烈、复杂多变的行业环境中努力开拓、锐意进取,以卓越的经营业绩、持续完善的全面风险…...

Java选择排序
选择排序是一种简单直观的排序算法,其基本思想是每一轮从待排序的元素中选择最小(或最大)的元素,将其与当前位置的元素交换。选择排序的实现步骤可以简要概括为: 初始化: 遍历整个数组,将当前位…...

[足式机器人]Part3 机构运动学与动力学分析与建模 Ch00-1 坐标系与概念基准
本文仅供学习使用,总结很多本现有讲述运动学或动力学书籍后的总结,从矢量的角度进行分析,方法比较传统,但更易理解,并且现有的看似抽象方法,两者本质上并无不同。 2024年底本人学位论文发表后方可摘抄 若有…...

【金猿人物展】DataPipelineCEO陈诚:赋能数据应用,发挥未来生产力
陈诚 本文由DataPipelineCEO陈诚撰写并投递参与“数据猿年度金猿策划活动——2023大数据产业年度趋势人物榜单及奖项”评选。 大数据产业创新服务媒体 ——聚焦数据 改变商业 我们处在一个“见证奇迹”的时代。在过去的20年间,我们见证了大数据技术快速发展所带…...
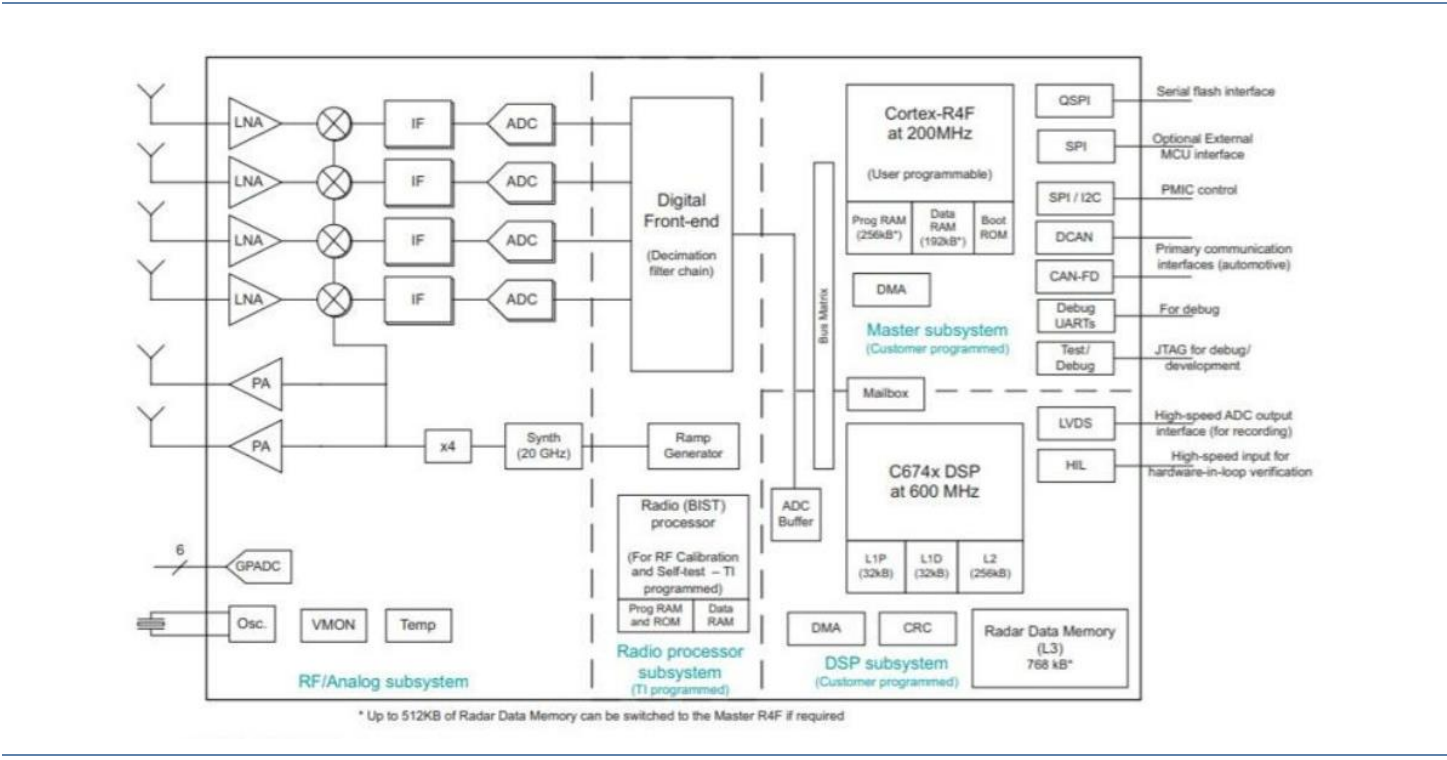
4D 毫米波雷达:智驾普及的新路径(二)
4 4D 毫米波的技术路线探讨 4.1 前端收发模块 MMIC:级联、CMOS、AiP 4.1.1 设计:级联、单芯片、虚拟孔径 4D 毫米波雷达的技术路线主要分为三种,分别是多级联、级联 虚拟孔径成像技术、以及 集成芯片。( 1 )多级…...

element plus自定义组件表单校验
方式一: import { formContextKey, formItemContextKey } from "element-plus";// 获取 el-form 组件上下文 const formContext inject(formContextKey, void 0); // 获取 el-form-item 组件上下文 const formItemContext inject(formItemContextKey, …...
函数,以将字符串s倒置。)
C //练习 4-13 编写一个递归版本的reverse(s)函数,以将字符串s倒置。
C程序设计语言 (第二版) 练习 4-13 练习 4-13 编写一个递归版本的reverse(s)函数,以将字符串s倒置。 注意:代码在win32控制台运行,在不同的IDE环境下,有部分可能需要变更。 IDE工具:Visual S…...
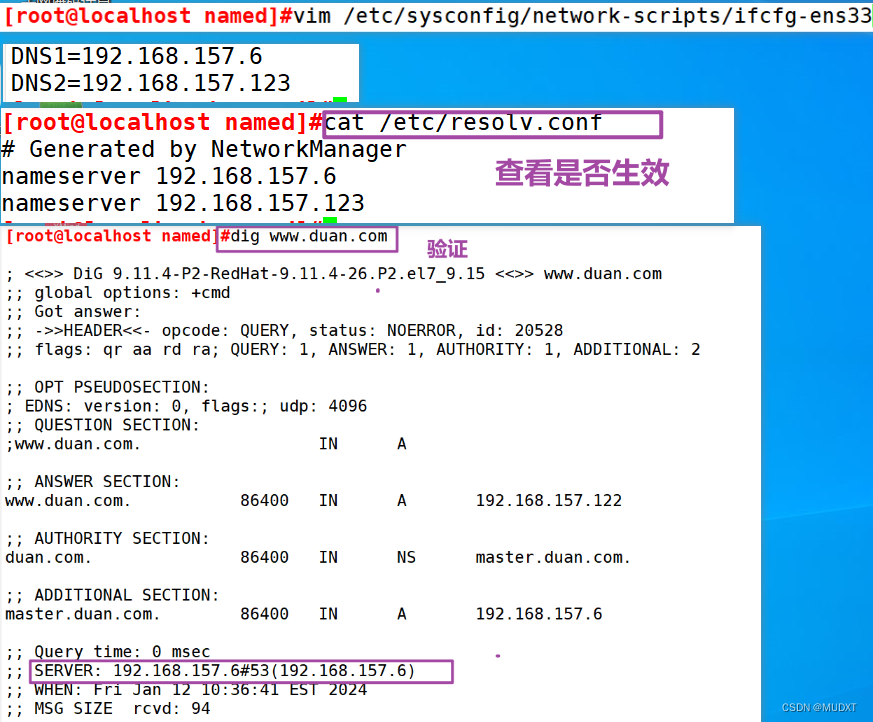
DNS解析和主从复制
一、DNS名称解析协议 二、DNS正向解析 三、DNS主从复制 主服务器 从服务器...
光猫(无限路由器)插入可移动硬盘搭建简易版的NAS
1.场景分析 最近查询到了许多有关NAS的资料,用来替代百度云盘等确实有很多优势,尤其是具有不限速(速度看自己配置)、私密性好、一次投入后续只需要电费即可等优势。鉴于手上没有可以用的资源-cpu、机箱、内存等,查询到…...

SpringIOC之support模块GenericGroovyApplicationContext
博主介绍:✌全网粉丝5W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验…...

Awesome 3D Gaussian Splatting Resources
GitHub - MrNeRF/awesome-3D-gaussian-splatting: Curated list of papers and resources focused on 3D Gaussian Splatting, intended to keep pace with the anticipated surge of research in the coming months. 3D Gaussian Splatting简明教程 - 知乎...
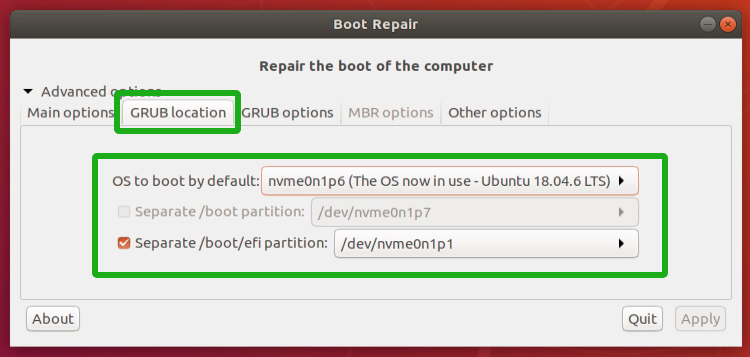
【镜像压缩】linux 上 SD/TF 卡镜像文件压缩到实际大小的简单方法(树莓派、nvidia jetson)
文章目录 1. 备份 SD/TF 卡为镜像文件2. 压缩镜像文件2.1. 多分区镜像文件的压缩(树莓派、普通 linux 系统等)2.2. 单分区镜像文件的压缩(Nvidia Jetson Nano 等) 3. 还原镜像文件到 SD/TF 卡4. 镜像还原后处理4.1. 镜像分区调整4…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
