数学的雨伞下:理解世界的乐趣
这本书没有一个公式,却讲透了数学的本质!
《数学的雨伞下:理解世界的乐趣》。一本足以刷新观念的好书,从超市到对数再到相对论,娓娓道来。对于思维空间也给出了一个更容易理解的角度。
作者:米卡埃尔•洛奈
原文完整版PDF:https://pan.quark.cn/s/019bf19c4981
备用链接:https://pan.xunlei.com/s/VNnuznqNbVUkAsfHkxcolkFdA1?pwd=pqe9#

这本书只有短短的五章,涉及十几个问题。无论从话题的有趣性,还是没什么数学基础读者的可读性都非常不错,我觉得将读书的过程称之为一场美妙的数学之旅非常合适。它非常好,好到什么程度,就是我看前面想到了一些可能补充的点,但是读到后面发现全都被囊括进去了。唯独的小遗憾可能是整本书的插图都非常“复古”,没那么精美又好像有点糊。不像一些书以没有公式作为卖点,附录中展示了每章真正的数学公式可供参考。
第一篇本福特定律,是个非典型的数字统计规律,我很惊讶它居然能被证明,且可用于检测一些数据造假。从生活中的超市开始的一个小发现,应用范围大的离谱。作者以绝对数值的大小比较,和人类相对感知之间的矛盾说起,将数字按照等间距的乘法进行排布,实际上得到了对数的分布——因为它能将乘法变成加法,还有我们熟知的纳皮尔的白皮书加速了世界的进程的故事。在没有数感的原始人或是动物身上做实验,也得到了类似的结果,从而得到世界可能是乘法的,常用如分贝、pH值等。这个定律也不会因为量度的变化而改变,因为本质上的相对关系是不变的。
第二篇可能有点跑题,海拔是如何定义的?数学里的反例思考有点像抬杠一样,尝试攻击每一个不严谨的地方,这样下去,“所有试图将现实梳理出头绪都可能复杂的令人绝望”。数学在做的事就是将包括数字在内的东西抽象成概念,以至于我们可以用不存在的东西去思考,书名雨伞是贯穿所有问题的思考方式。
海岸线有多长?或是书中所说的边境长度,从各地的数据中发现巨大的差异,此时曼德勃罗(书中译为曼德博)写下了那篇经典文章。在讲无穷大时作者没用经典的希尔伯特旅馆例子,用买巧克力来举例。讲到分形几何就不得不先提到维度,再次呼应了对数的尺度部分。
书中有一句话我很喜欢,“数学不在乎什么是显而易见的,它只想知道什么是真的。”从主观上我不太能接受数学是模糊的,当然这与模糊数学的分支无关,它定义应当是清晰准确的,作者又确实说服了我。他用非常容易的例子逐步引入球面几何。最后一章从光速不变理论到无穷,你可能感觉没学到什么知识,这个例子也许会在你未来学习的时候潜移默化的浮现,这样就足够了。

研究数学,就是创造想象的世界,在这些世界中,我们的思维可以自由漫步,不必担心现实的妨碍。这种思维方式虽然涵盖的范围要广得多,但和尼普尔人在加法世界中用来简化乘法的思维方式非常相似。当你碰到一个科学问题时,下面这种解决方法往往会很有效:
1. 创造一个数学世界,你可以在这个世界里把问题模型化;
2. 在这个数学世界里解决问题;
3. 把结果转回到现实世界中。
比如说,这种通用的方法就被天文学家用来了解行星的轨迹或预测日食(图 2.8)。
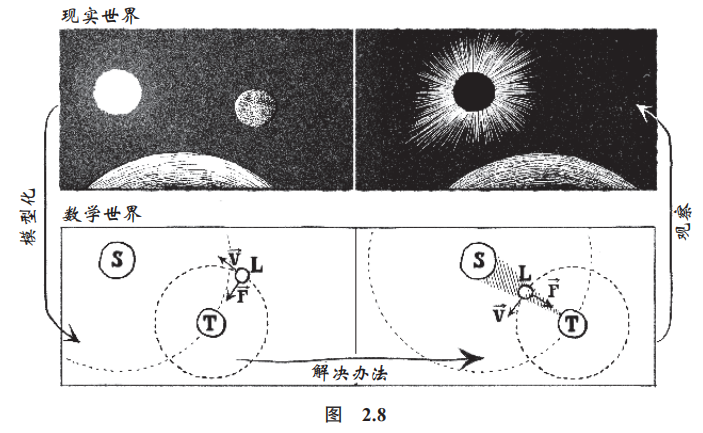
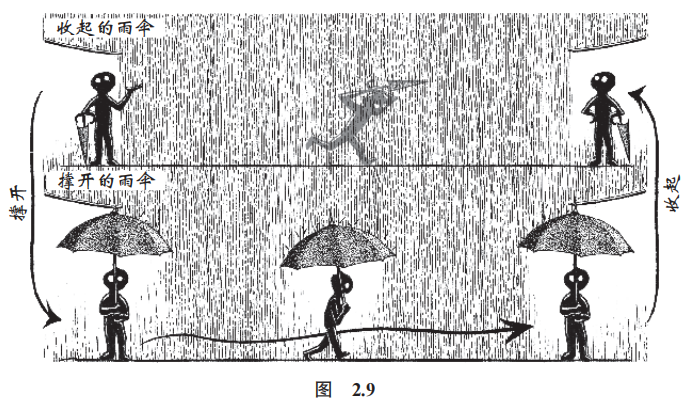
这种解决问题的模式叫作“雨伞定理”。如果你在雨天想要在不被淋湿的情况下从一个地方前往另一个地方,请按照以下步骤操作(图 2.9):
1. 撑开你的雨伞;
2. 开始你的行程;
3. 收起你的雨伞。
步骤 1 和步骤 3 的操作是相反的,如果你能够在雨伞为你打开的特定世界中达成预期的目标,那么你在操作结束时就会恢复到开始时的状态。负数的雨伞为地理学家测量海拔提供了研究上的便利。对数的雨伞让淹没在乘法中的天文学家得以进入加法的世界。而更广泛地说,抽象的雨伞为所有科学家进入数学世界提供了可能。
在接下来的路途中,我们还会用到很多雨伞。雨伞,是观点的改变,是差异,是从另一个角度看待事物的艺术,一种更适合、更有效的角度。
走得更远,并不总是意味着长久而乏味的努力,而是首先要找到解决所面临的问题的正确方法。如果我们以正确的方式看待问题,那么最错综复杂的问题也会在一瞬间变得简单明了。伟大的智者能尽显其才,首先是因为他们拥有在正确的时间发明正确的雨伞的能力。
在 18 世纪,古怪的作家和旅行家乔纳斯·汉韦(Jonas Hanway)是第一个使用雨伞的伦敦人。这是一把真的雨伞——挡雨的伞。他为此遭受了很多白眼和伦敦马车夫赤裸裸的恶意,因为在当时,搭乘马车一直是在糟糕天气出行而不会被淋湿的唯一方法。毫不畏惧旁人眼光的汉韦继续自豪地使用了三十多年的雨伞,并慢慢看到他的同胞们也开始使用雨伞。在他去世后几个月,第一批商业化雨伞出现在英国,并获得了我们今日所知的成功。
不要惧怕与众不同,这就是雨伞的智慧。让我们无所畏惧,既不感到羞耻,也不抱有偏见。一旦接受在头顶撑起抽象的雨伞并进入数学的世界,我们就不会再全然依赖现实。不必让自己陷在无用的限制或令人尴尬的既有观念之中。你想要一个 4 月 34 号吗?拿去吧!你想要负数吗?拿去吧!你想要无穷吗?拿去吧!如果所有这些想法不会干扰你组织思维,甚至还有所帮助,那为什么要剥夺它们呢?你是自由的!
如此自由,甚至容易让人头晕目眩。在这一点上,数学和一大盘点心有着异曲同工之妙——选择太多,就难以做出选择了。懂得如何在数学世界里自我驾驭,是一种需要实践和直觉的能力。
为此,数学家制造出很多导航工具,其中有两个指南针:一个名叫“实用”,一个名叫“优雅”。“实用”引导我们创造出最贴近现实的抽象世界,在这些抽象世界中进行的研究能够轻松地转化为关于我们宇宙的知识。“优雅”告诉我们要完全抛开现实,并沉醉在抽象世界的奇观中。那里有许许多多美丽的事情要做——如果一件事是无用的,那它就更美了。
每个人都能以自己的方式使用这两个指南针。有些人偏爱其中的某一个,有些人则两个一起用,并不断在两个指南针指示的方向之间寻找完美的平衡。但世界充满奥秘,因此,探索实用之人和探索优雅之人常常会在走过不同的道路之后,在同一个地方不期而遇。看到大自然如此喜爱按照优雅的数学原理运转,真是既让人目瞪口呆,又让人不知所措。
原文很长,这里只是节选了其中一部分内容,完整版PDF已整理好了,感兴趣的小伙伴可以去看看。
相关文章:

数学的雨伞下:理解世界的乐趣
这本书没有一个公式,却讲透了数学的本质! 《数学的雨伞下:理解世界的乐趣》。一本足以刷新观念的好书,从超市到对数再到相对论,娓娓道来。对于思维空间也给出了一个更容易理解的角度。 作者:米卡埃尔•洛奈…...
)
补充 vue3用户管理权限(路由控制)
之前有人问我 ,如果是二级路由如何添加,这里我做一个补充吧。直接拿方法去用就行。也不做解释了。稍微看下就能看懂了 假设,后端返回给我们一个数据 [“/defa”,"/defa/defa1"] 这样的一个路由表,我们就需要通过这个路…...
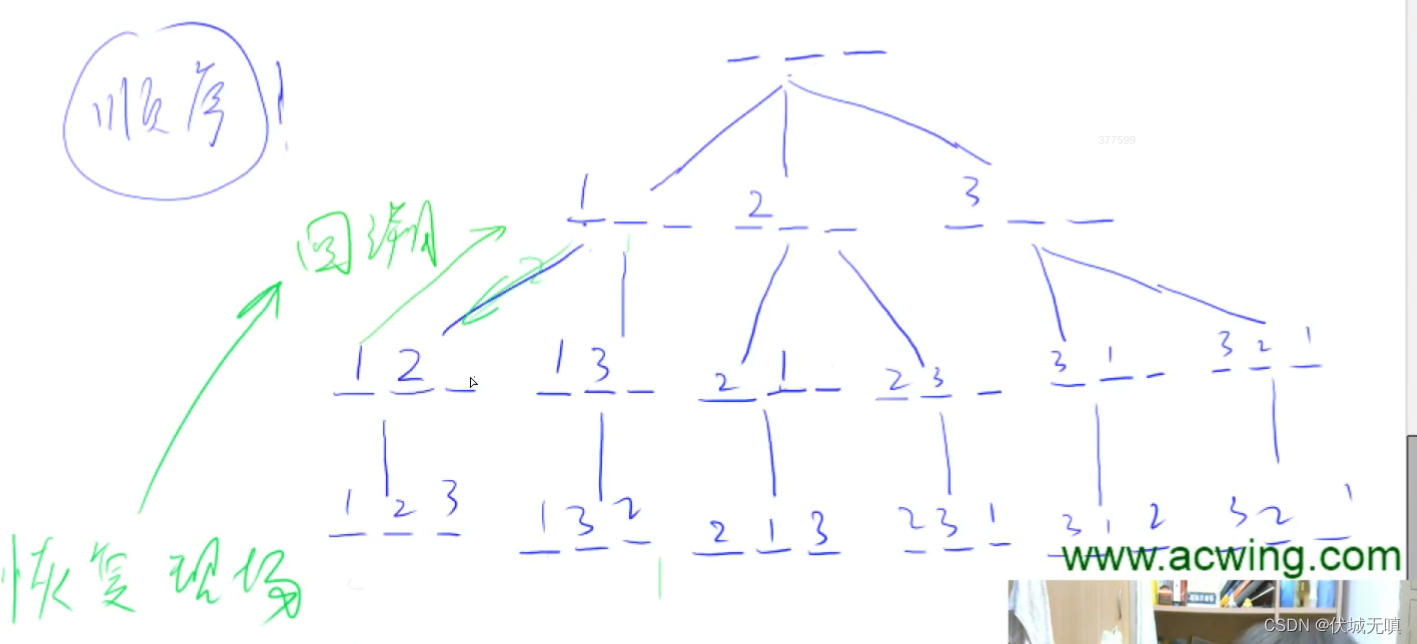
C++ 深度优先搜索DFS || 模版题:排列数字
给定一个整数 n ,将数字 1∼n 排成一排,将会有很多种排列方法。 现在,请你按照字典序将所有的排列方法输出。 输入格式 共一行,包含一个整数 n 。 输出格式 按字典序输出所有排列方案,每个方案占一行。 数据范围 1…...
计算机找不到msvcp120.dll如何解决?总结五个可靠的教程
在计算机使用过程中,遇到“找不到msvcp120.dll”这一问题常常令人困扰。msvcp120.dll作为Windows系统中至关重要的动态链接库文件,对于许多应用程序的正常运行起着不可或缺的作用。那么,究竟是什么原因导致找不到msvcp120.dll呢?又…...

法线变换矩阵的推导
背景 在冯氏光照模型中,其中的漫反射项需要我们对法向量和光线做点乘计算。 从顶点着色器中读入的法向量数据处于模型空间,我们需要将法向量转换到世界空间,然后在世界空间中让法向量和光线做运算。这里便有一个问题,如何将法线…...
React.Children.map 和 js 的 map 有什么区别?
JavaScript 中的 map 不会对为 null 或者 undefined 的数据进行处理,而 React.Children.map 中的 map 可以处理 React.Children 为 null 或者 undefined 的情况。 React 空节点:可以由null、undefined、false、true创建 import React from reactexport …...

13.Kubernetes部署Go应用完整流程:从Dockerfile到Ingress发布完整流程
本文以一个简单的Go应用Demo来演示Kubernetes应用部署的完整流程 1、Dockerfile多阶段构建 Dockerfile多阶段构建 [root@docker github]# git clone https://gitee.com/yxydde/http-dump.git [root@docker github]# cd http-dump/ [root@docker http-dump]# cat Dockerfile …...
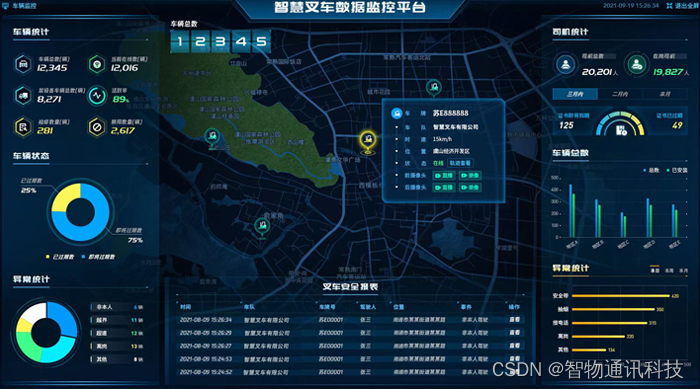
叉车车载终端定制_基于MT6762安卓核心板的车载终端设备方案
叉车车载终端是一款专为叉车车载场景设计的4英寸Android车载平板电脑。它采用了高能低耗的8核ARM架构处理器和交互开放的Android 12操作系统,算力表现强大。此外,该产品还具备丰富的Wi-Fi-5、4G LTE和蓝牙等通讯功能,可选配外部车载蘑菇天线&…...
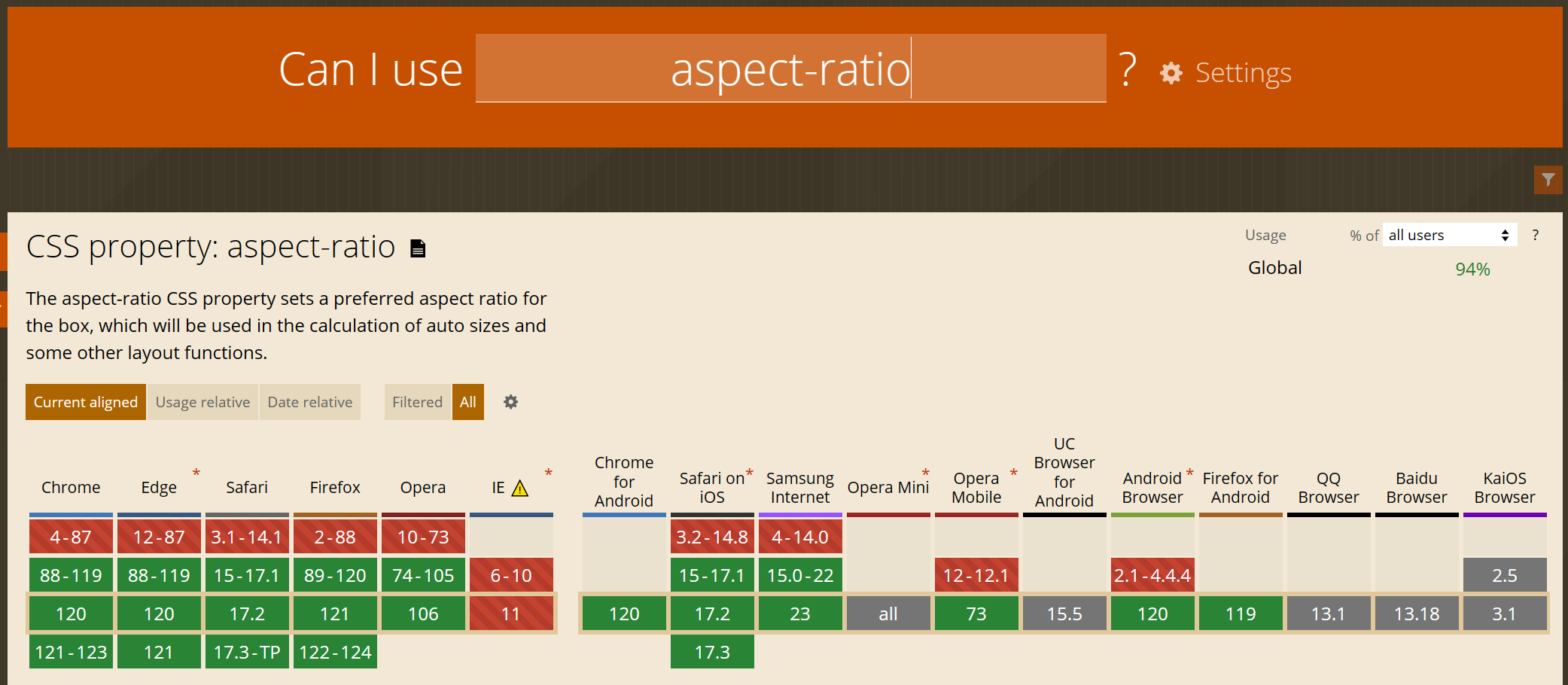
【CSS】保持元素宽高比
保持元素的宽高比,在视频或图片展示类页面是一个重要功能。 本文介绍其常规的实现方法。 实现效果 当浏览器视口发生变化时,元素的尺寸随之变化,且宽高比不变。 代码实现 我们用最简单的元素结构来演示,实现宽高比为4…...

使用 Docker 和 Diffusers 快速上手 Stable Video Diffusion 图生视频大模型
本篇文章聊聊,如何快速上手 Stable Video Diffusion (SVD) 图生视频大模型。 写在前面 月底计划在机器之心的“AI技术论坛”做关于使用开源模型 “Stable Diffusion 模型” 做有趣视频的实战分享。 因为会议分享时间有限,和之前一样,比较简…...

C++ namespace高级用法
高级用法 C++中的命名空间(namespace)是一种用于组织代码的机制,它可以帮助避免命名冲突,并使代码更加清晰和易于维护。以下是C++命名空间的一些高级用法: 嵌套命名空间:命名空间可以嵌套在其他命名空间中,形成一个层次结构。嵌套命名空间可以进一步细化命名空间,使其更…...

如何允许远程访问 MySQL
前些天发现了一个人工智能学习网站,通俗易懂,风趣幽默,最重要的屌图甚多,忍不住分享一下给大家。点击跳转到网站。 如何允许远程访问 MySQL 现在许多网站和应用程序一开始的 Web 服务器和数据库后端都托管在同一台计算机上。随着…...

PostgreSQL认证考试PGCA、PGCE、PGCM
PostgreSQL认证考试PGCA、PGCE、PGCM 【重点!重点!重点!】PGCA、PGCE、PGCM 直通车快速下正,省心省力,每2个月一次考试 PGCE考试通知 (2024) 一、考试概览 (一) 报名要…...
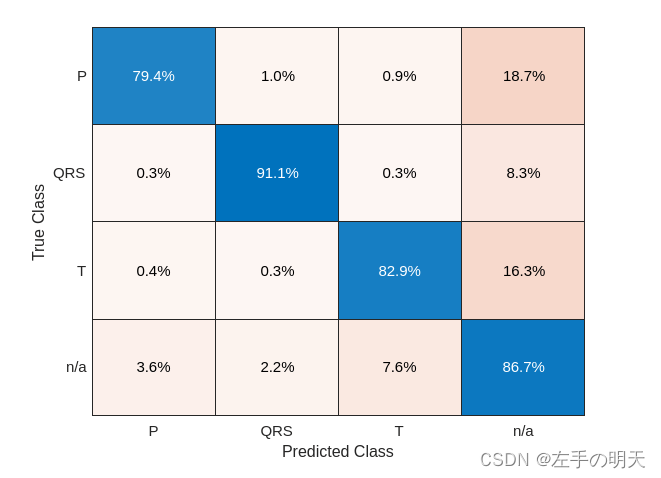
Matlab深度学习进行波形分割(二)
🔗 运行环境:Matlab 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 🔐#### 防伪水印——左手の明天 ####🔐 💗 大家…...

Markdown高级用法——mermaid
Markdown高级用法——mermaid 起初是写文章,其中有时序图流程图等一般是processOn或者draw.io画截图粘过去的,工作中又是腾讯文档,上面也能画图,但假如我笔记软件用语雀之类的又要把一张图反复粘贴,浪费内存ÿ…...

cf919Div2C题题目总结
Problem - C - Codeforces 这道题其实是一道数学题。 先看第一个变量,也就是我们要求的答案k的数量,但看k是很好确定它的限制条件的,要想均匀分成k份,n%k必须为0,有了k,我们再来看m,对于a(1)和…...

Pandas实战100例 | 案例 4: 数据选择和索引 - 选择特定的列和行
案例 4: 数据选择和索引 - 选择特定的列和行 知识点讲解 在 Pandas 中,选择数据是一个非常常见的操作。你可以选择特定的列或行,或者基于某些条件筛选数据。 示例代码 选择特定的列 # 选择单列 selected_column df[ColumnName]# 选择多列 selected…...

Netty-Netty实现自己的通信框架
通信框架功能设计 功能描述 通信框架承载了业务内部各模块之间的消息交互和服务调用,它的主要功能如下: 基于 Netty 的 NIO 通信框架,提供高性能的异步通信能力; 提供消息的编解码框架,可以实现 POJO 的序列化和反…...

【算法刷题】总结规律 算法题目第2讲 [234] 回文链表,因为深浅拷贝引出的bug
配合b站视频讲解食用更佳:https://www.bilibili.com/video/BV1vW4y1P7V7 核心提示:好几道题是处理有序数组的! 适合人群:考研/复试/面试 解决痛点:1. 刷了就忘 2.换一道相似的题就不会 学完后会输出:对每类题目的框架…...

RabbitMQ如何保证消息不丢失?
RabbitMQ如何保证消息不丢失? 消息丢失的情况 生产者发送消息未到达交换机生产者发送消息未到达队列MQ宕机,消息丢失消费者服务宕机,消息丢失 生产者确认机制 解决的问题:publisher confirm机制来避免消息发送到MQ过程中消失。…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
