Qt中QByteArray之元素访问
访问QByteArray类对象中的某个元素主要有4种方式,分别为[]、at()、 data[]和constData[]。其中,[]和data]]方式为可读可写,at()和constData[]方式仅为可读。如果只是进行读操作,则通过at()和constData[]方式的访问速度最快,因为避免了复制处理。at()可以比operator [0更快,就是因为前者不会发生深层复制。
#include <QCoreApplication>
#include <qDebug>
int main(int argc, char *argv[]){
QCoreApplication a(argc, argv);
QByteArray bal ("Hello");
if('\0'==bal[5])printf ("bal [5]=\'\\٥\'\n");
QByteArray ba;
ba.resize(6);
ba [0] = 0x3c;
ba [1] = 0xb8;
ba [2] = 0x64;
ba [3] = 0x18;
ba[4] = 0xca;
ba.data () [5] = 0x31;
qDebug ()<<" []"<<ba[2]; //[] d
dqDebug ()<<"at ()"<<ba.at (2); //at() d
qDebug ()<<"data () "<<ba.data () [2]; //data () d
dqDebug ()<<"constData ()"<<ba.constData () [2]; //constData () d
dqDebug ()<<"constData ()"<<ba.constData () [5]; //constData () 1
return a.exec ();
}
qDebug()会输出ba[2]对应的字符,ASCII码为Ox64的字符是'd'。
相关文章:

Qt中QByteArray之元素访问
访问QByteArray类对象中的某个元素主要有4种方式,分别为[]、at()、 data[]和constData[]。其中,[]和data]]方式为可读可写,at()和constData[]方式仅为可读。如果只是进行读操作,则通过at()和constData[]方式的访问速度最快,因为避…...
java实现教务管理系统
git地址:https://gitee.com/myshort-term/school-management 1.系统简介 开发教务管理系统程序,设计了ems(EMSApp)、dao(AssignmentDAO、CourseDAO、DeptDAO、ScoreDAO、UserDAO、EmailDAO)、domain&#…...
NPS配置https访问web管理页面
因为NPS默认也支持http的访问,所以在部署完后就一直没在意这个事情。 因为服务器是暴露在公网内的,所以还是要安全一点才行。不然一旦远控的机器被破解了就很危险了 一、使用nginx反向代理访问 1、首先在nps的配置文件里关闭使用https选项,…...
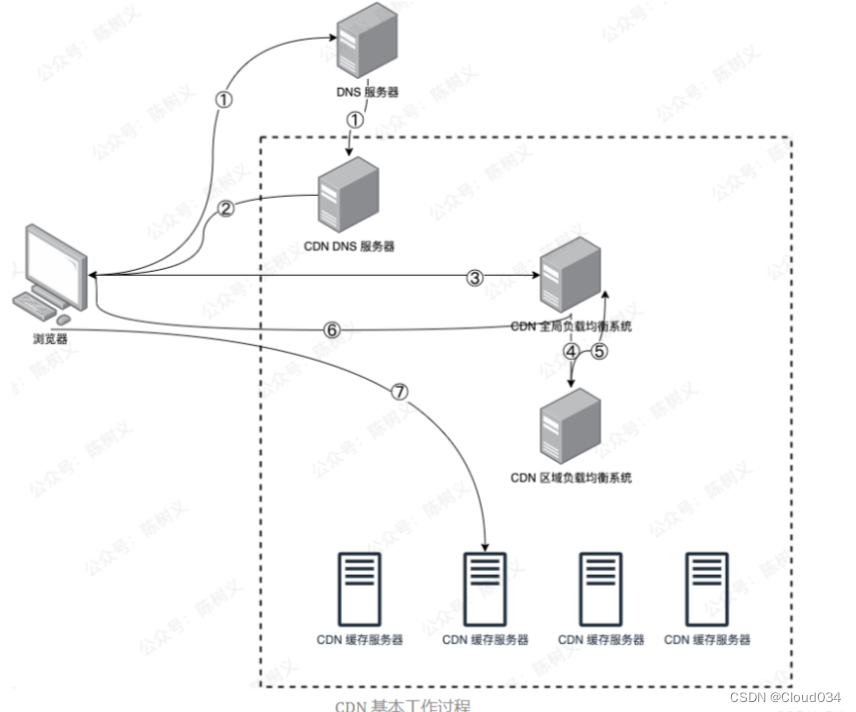
nginx和CDN应用
一、代理的工作机制 1.代替客户机向网站请求数据,从而可以隐藏用户的真实IP地址。 2.将获得的网页数据(静态 Web 元素)保存到缓存中并发送给客户机,以便下次请求相同的数据时快速响应。 二、代理服务器的…...

Keil5如何生成反汇编文件
Keil5如何生成反汇编文件 在Keil5界面下点击选项,选择“User”,勾选“After Build/Rebuild”中“RUN #1”,复制fromelf --text -a -c --outputxxx.dis xxx.axf 在Linker栏中找到“Linker Control string”里最后-o后的.axf文件,将…...
网络地图服务(WMS)详解
文章目录 1.概述2.GetCapabilities3.GetMap4.GetFeatureInfo 阅读本文之前可参考前文:《地图服务器GeoServer的安装与配置》与《GeoServer发布地图服务(WMS、WFS)》。 1.概述 经过前文的介绍,相信我们对WMS/WFS服务已经有了一个非…...
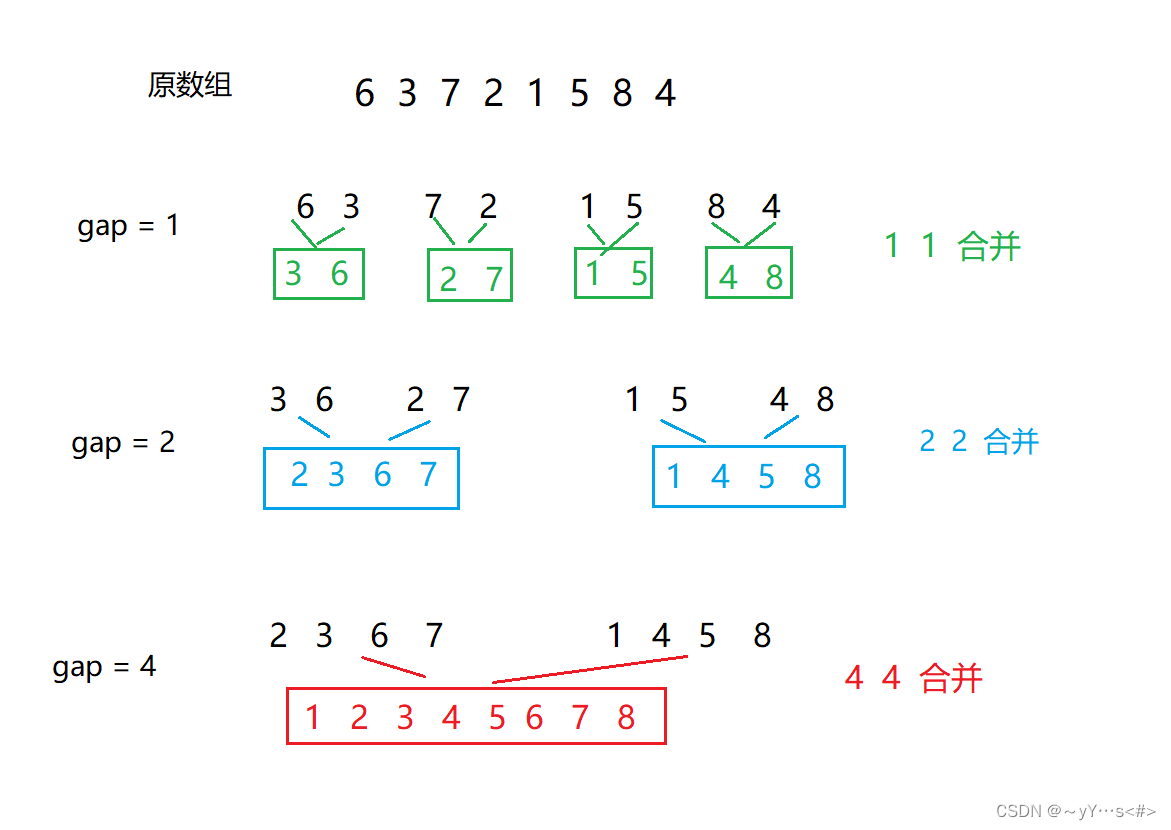
【排序篇3】快速排序、归并排序
目录 一、快速排序1.1 递归1.2 非递归 二、归并排序2.1 递归2.2 非递归 一、快速排序 1.1 递归 快速排序的递归采用二叉树的前序遍历的思路,单趟排序先确定好一个元素的位置,然后往后递归再确定其他子区域内的某个元素的位置,直到只有一个元…...

Python中的@property
在 Python 中,property 是一种装饰器,用于将一个方法转换成只读属性。通过使用 property 装饰器,你可以定义一个类的方法,使其在访问时可以像访问属性一样,而不是通过方法调用。 下面是一个简单的例子来说明 property …...
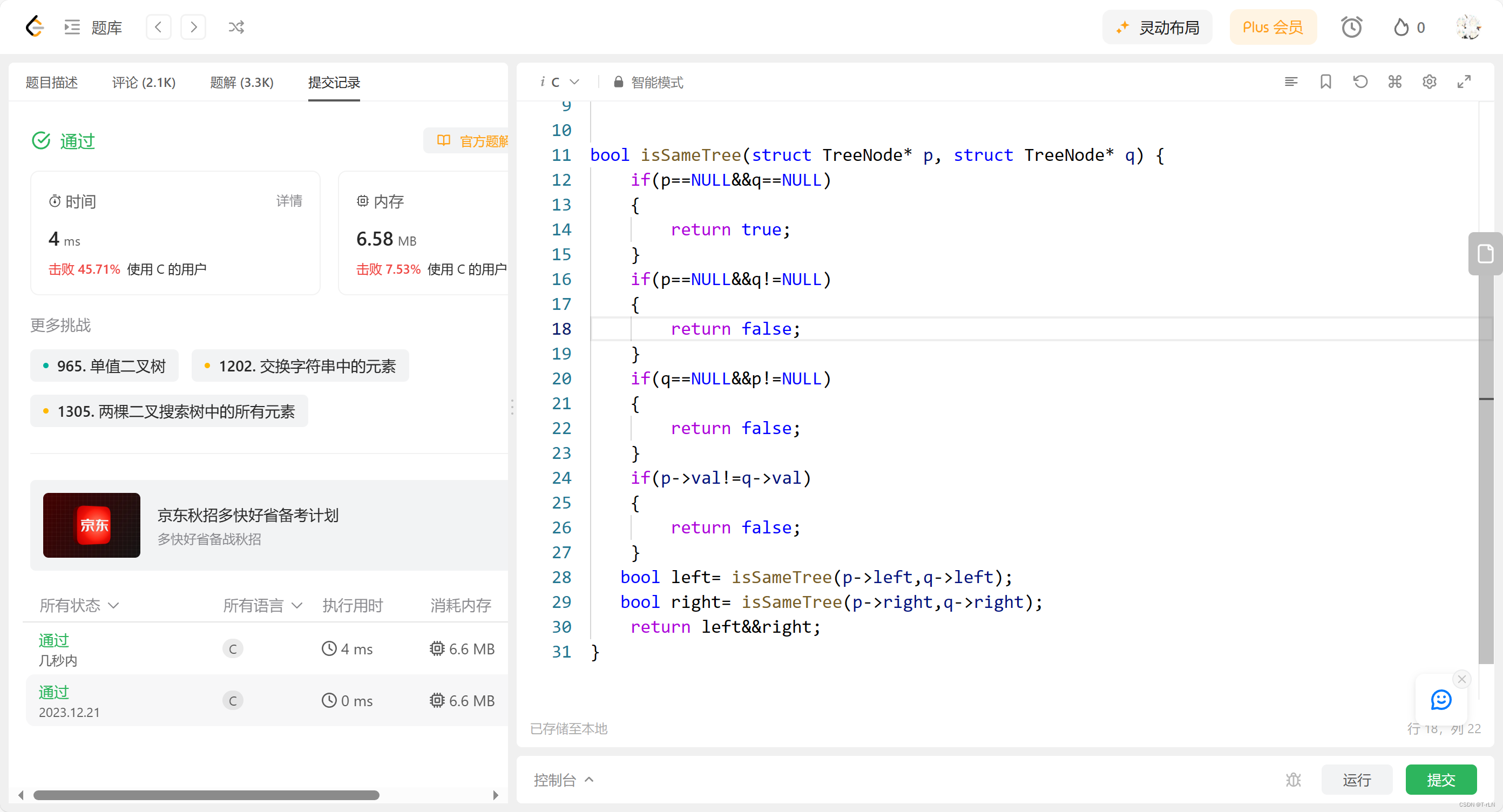
二叉树基础oj练习(单值二叉树、相同的树、二叉树的前序遍历)
讲了这么多数据结构相关的知识(可以看我的数据结构文章专栏): 抓紧刷题巩固一下了 目录 1.单值二叉树 题目描述 思路1 代码1 思路2 代码2 2.相同的树 题目描述 思路 代码 3.二叉树的前序遍历 代码 思路 1.单值二叉树 965. 单值二叉树 - 力扣(LeetCod…...
自动化创建ETX用户帐号
在芯片设计行业,ETX是常见的远程访问环境。用户在通过ETX访问远程环境前必须首先加入ETX系统,然后通过profile分配相关的环境的访问权限。 通常这些操作在ETX WEB页面手工操作,如果我们期望实现用户帐号注册全自动化,就需要将以上…...

Android 实现集合去重的方法
方法一:使用HashSet 将集合转换为HashSet。 Set<String> set new HashSet<>(list);将HashSet转换回List。 List<String> uniqueList new ArrayList<>(set);方法二:使用Java 8的Stream API 将列表转换为Stream。 Stream&l…...
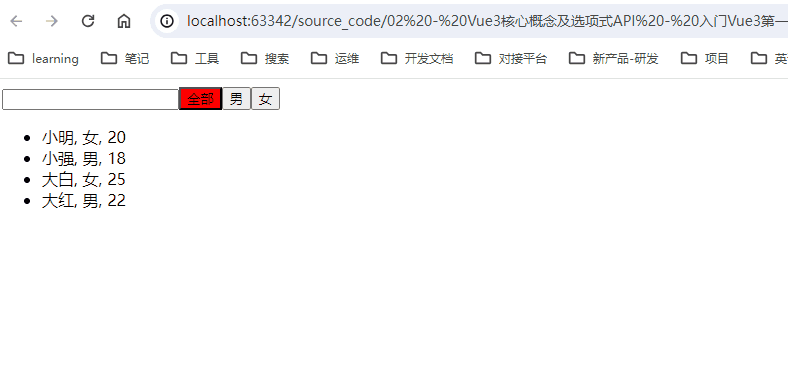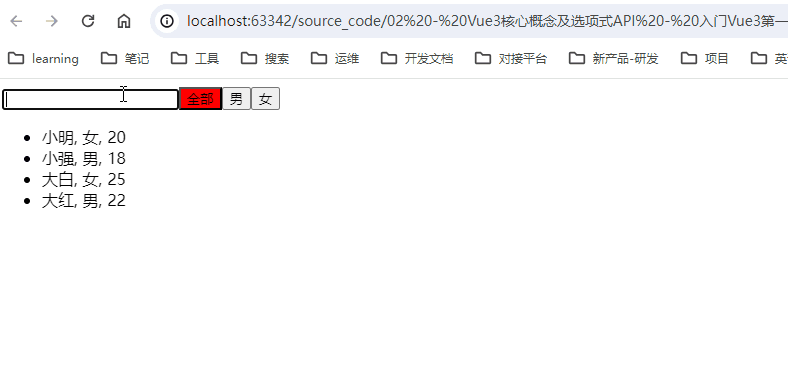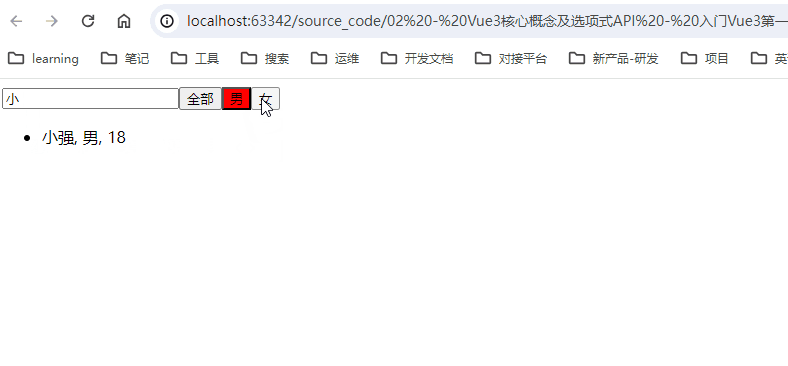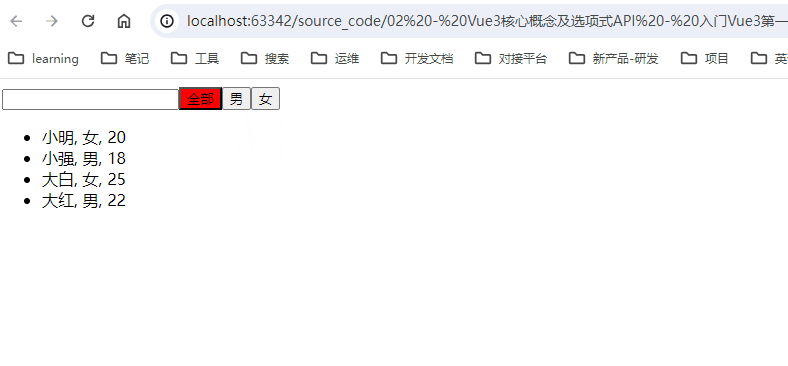
【Vue3】2-12 : 【案例】搜索关键词加筛选条件的综合
本书目录:点击进入 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 1.2、效果 1.3、json数据 - 02-data.json 1.4、代码 一、【案例】搜索关键词加筛选条件的综合 1.1、逻辑 计算属性 - 绑定list,并过滤 input 双向绑定 - 当input改变时&…...
unity小程序websocket:nginx配置https (wss)转http (ws)及其他问题解决
目录 前言 实际运用场景 处理流程如下 nginx配置ssl和wss 配置过程中遇到的问题 1、无法连接服务器 2、通过IP可以访问,域名却不行 问题描述 解决 3、如何判断该域名是否备案了 前言 为了服务器网络的通用性,我们在实现移动端的游戏转微信小程序…...

MySql数据库对接Orcal数据库,需要考虑的前提问题
1.主表 从表的表关系;主键id 的关联问题; 2.字段类型的一致性问题(备注:像varchar类型的一点要谨防数据过长抛错); 3.实体类字段两表一致性问题; 4.入表不为空问题,判空尽量在实体…...

K8S的存储卷---数据卷
容器内的目录和宿主机的目录进行挂载 容器在系统上的生命周期是短暂的。delete,K8S用控制器创建的pod,delete相当于重启,容器的状态也会恢复到初始状态。一旦回到初始状态,所有的后天编辑的文件都会消失 容器和节点之间创建一个…...

【量化交易故事】小明开启了量化创业之旅-01
故事开始于2023年的春天,小明是一位对金融市场充满热情的IT工程师。在经历了数次基于主观判断和个人情绪进行投资却收获平平后,他意识到传统交易方式中的人为因素难以避免,而这往往成为影响投资决策稳定性和准确性的关键障碍。在一次偶然的机…...

ffmpeg写YUV420文件碰到阶梯型横线或者条纹状画面的原因和解决办法
版权声明:本文为CSDN博主「文三~」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/asdasfdgdhh/article/details/112831581 看到了,转载,留着备份…...
案例:新闻数据加载
文章目录 介绍相关概念相关权限约束与限制完整示例 代码结构解读构建主界面数据请求下拉刷新总结 介绍 本篇Codelab是基于ArkTS的声明式开发范式实现的样例,主要介绍了数据请求和touch事件的使用。包含以下功能: 数据请求。列表下拉刷新。列表上拉加载…...
数学的雨伞下:理解世界的乐趣
这本书没有一个公式,却讲透了数学的本质! 《数学的雨伞下:理解世界的乐趣》。一本足以刷新观念的好书,从超市到对数再到相对论,娓娓道来。对于思维空间也给出了一个更容易理解的角度。 作者:米卡埃尔•洛奈…...
)
补充 vue3用户管理权限(路由控制)
之前有人问我 ,如果是二级路由如何添加,这里我做一个补充吧。直接拿方法去用就行。也不做解释了。稍微看下就能看懂了 假设,后端返回给我们一个数据 [“/defa”,"/defa/defa1"] 这样的一个路由表,我们就需要通过这个路…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
