当前位置： 首页 > news >正文

概率论与数理统计————1.随机事件与概率

news 2025/11/4 22:20:57

一、随机事件

随机试验：满足三个特点

（1）可重复性：可在相同的条件下重复进行

（2）可预知性：每次试验的可能不止一个，事先知道试验的所有可能结果

（3）不确定性：每次试验不能确定实验结果

随机试验记作E

样本空间：随机试验E的所有可能的结果构成的集合

样本点：样本空间的每个元素是一个样本点

随机事件：样本空间的子集为一个随机事件（事件放生：该事件的某个样本点出现）

必然事件：必然发生的事件

不可能事件：不可能发生的事件

二、事件间的关系和运算

1、包含

A\subsetB：事件A发生，则事件B必发生

A=B      < = >    A\subset B且B\subset A

2.事件的和（并）

A\cupB 或A+B :  事件A和事件B至少发生一个

3、事件的积（交）

AB或A\capB :  事件A和事件B同时发生

4、事件的差

A-B：事件A发生了，事件B不发生

重要公式：A-B=A-AB

5、互不相容事件

A和B互斥则A和B没有交集

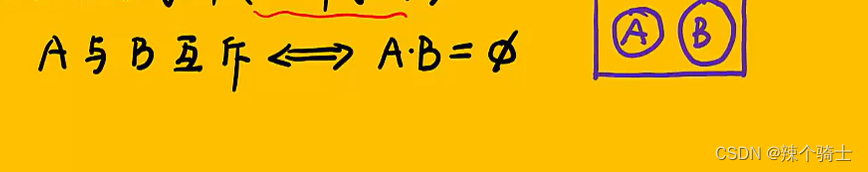
6、对立事件

交换律：A\cup B=B\cup A,A\cap B=B\cap A

结合律：(A\cup B)\cup C,A\cup (B\cup C)  ,        A\cap B\cap C=A\cap (B\cap C)

分配律：(A\cup B)\cap C=(A\cap C)\cup (B\cap C )

             (A\cap B)\cup C=(A\cup C)\cap (B\cup C)

德摩根律：

三、概率的定义和性质

设一个随机试验，重复做n次，A为随机事件，发生m次则

\frac{m}{n}=p为A发生的频率，当试验次数足够大时，p为事件A发生的概率

非负性：0\leq p\leq 1

规范性：P（s）=1；p（\o\O\not{o}）=0

有限可加性：若A,B互斥，则p（A\cupB）=P（A）+P（B）

互补性：P（\bar{A}）=1-P(A)

减法公式：p（A-B）=p（A）-p（AB）

加法公式：p（A\cup B）=p（A）+p（B）-p（AB）

相关文章：

概率论与数理统计————1.随机事件与概率

一、随机事件 随机试验&#xff1a;满足三个特点 &#xff08;1&#xff09;可重复性&#xff1a;可在相同的条件下重复进行 &#xff08;2&#xff09;可预知性&#xff1a;每次试验的可能不止一个&#xff0c;事先知道试验的所有可能结果 &#xff08;3&#xff09;不确定…...

编程日记 2024/1/15 6:55:08

【生存技能】git操作

先下载git https://git-scm.com/downloads 我这里是win64&#xff0c;下载了相应的直接安装版本 64-bit Git for Windows Setup 打开git bash 设置用户名和邮箱 查看设置的配置信息 获取本地仓库 在git bash或powershell执行git init&#xff0c;初始化当前目录成为git仓库…...

编程日记 2024/1/15 6:53:06

docker 将镜像打包为 tar 包

目录 1 实现 1 实现 要将镜像导出为.tar包&#xff0c;可以使用Docker命令行工具进行操作。下面是导出镜像的步骤&#xff1a; 首先&#xff0c;使用以下命令列出当前系统上的镜像&#xff0c;并找到要导出的镜像的ID或名称&#xff1a; docker images使用以下命令将镜像导出为…...

编程日记 2024/1/15 6:52:05

341. 最优贸易(dp思想运用，spfa，最短路)

341. 最优贸易 - AcWing题库 C 国有 n 个大城市和 m 条道路&#xff0c;每条道路连接这 n 个城市中的某两个城市。 任意两个城市之间最多只有一条道路直接相连。 这 m 条道路中有一部分为单向通行的道路&#xff0c;一部分为双向通行的道路&#xff0c;双向通行的道路在统计…...

编程日记 2024/1/15 6:50:03

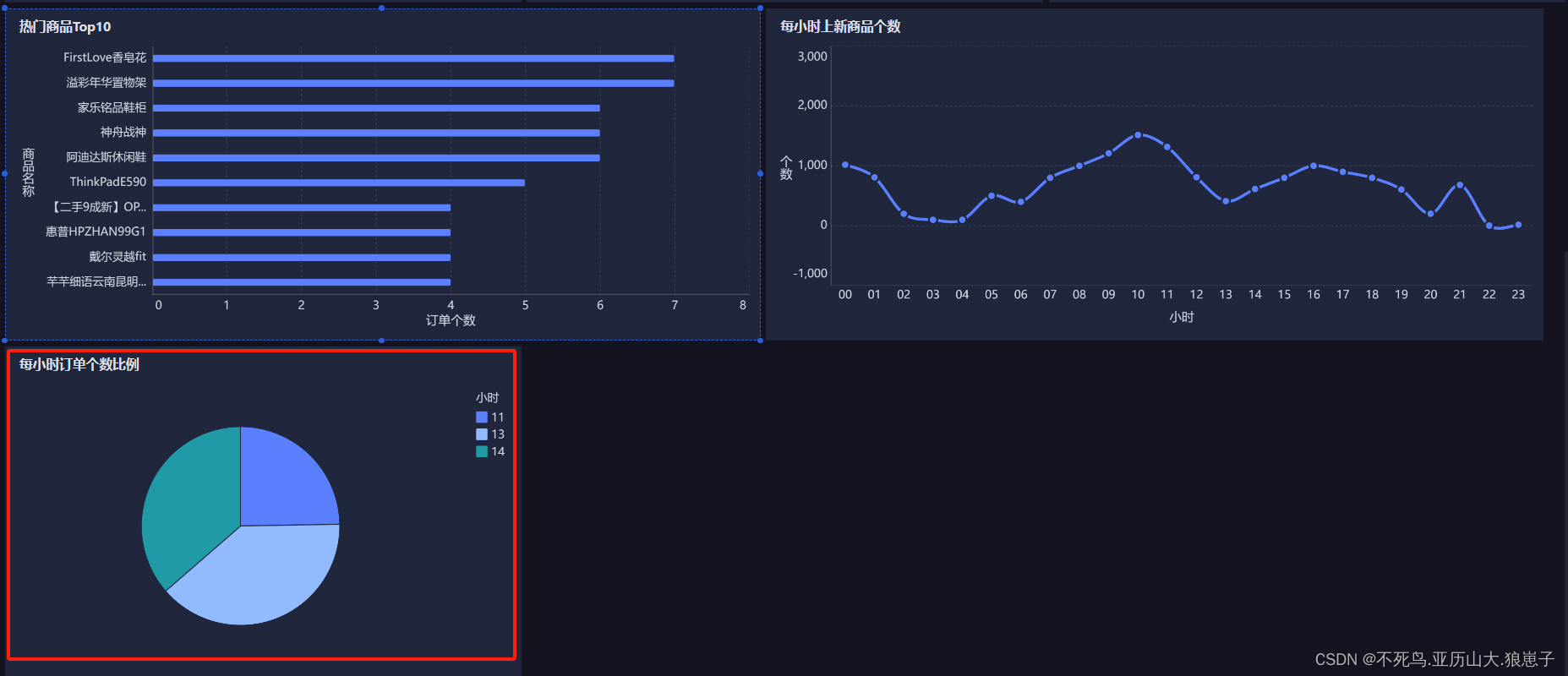
FineBI实战项目一（19）：每小时订单笔数分析开发

点击新建组件&#xff0c;创建下每小时订单笔数组件。 选择饼图&#xff0c;拖拽cnt&#xff08;总数&#xff09;到角度&#xff0c;拖拽hourstr到颜色&#xff0c;调节内径。 修改现在的文字 拖拽组件到仪表盘。 效果如下&#xff1a;...

编程日记 2024/1/15 6:49:02

What is `@RequestBody ` does?

RequestBody 是SpringMVC框架中的注解&#xff0c;通常与POST、PUT等方法配合使用。当客户端发送包含JSON或XML格式数据的请求时&#xff0c;可以通过该注解将请求体内容绑定到Controller方法参数上 作用 自动反序列化&#xff1a; SpringMVC会根据RequestBody注解的参数类型&…...

编程日记 2024/1/15 6:48:01

Windows安装Rust环境（详细教程）

一、 安装mingw64(C语言环境) Rust默认使用的C语言依赖Visual Studio&#xff0c;但该工具占用空间大安装也较为麻烦&#xff0c;可以选用轻便的mingw64包。 1.1 安装地址 (1) 下载地址1-GitHub&#xff1a;Releases niXman/mingw-builds-binaries GitHub (2) 下载地址2-W…...

编程日记 2024/1/15 6:44:58

Marin说PCB之传输线损耗---趋肤效应和导体损耗01

大家在做RF上的PCB走线或者是车载相机的上走线的时候经常会听那些硬件工程师们说你这个走线一定要保证50欧姆的阻抗匹配啊&#xff0c;还有就是记得加粗走做隔层参考。 有的公司的EE硬件同事会很贴心的把RF走线的注意事项给你备注在原理图上或者是layoutguide上&#xff0c;遇到…...

编程日记 2024/1/15 6:42:56

八：分布式锁

1、为什么要使用分布式锁 锁是多线程代码中的概念&#xff0c;只有多任务访问同一个互斥的共享资源时才需要锁。单机应用开发时一般使用synchronized或lock。多线程的运行都是在同一个JVM之下。应用是分布式集群&#xff0c;属于多JVM的工作环境&#xff0c;JVM之间已经无法通过…...

编程日记 2024/1/15 6:40:54

示例：php将文本内容写入一个文件(面向过程写法)

一、封装2个函数&#xff0c;读写文件 /*** desc 读取文件内容* param string $filename* return array*/ private function readContent(string $filename): array {$text file_get_contents($filename);if (!$text) {return [];}$result json_decode($text,true);return…...

编程日记 2024/1/15 6:38:52

Flutter开发进阶之并发操作数据库

Flutter开发进阶之并发操作数据库 尽管 Flutter 本身不包含任何数据库功能&#xff0c;但可以使用各种第三方库和插件来在 Flutter 应用程序中实现数据库功能&#xff1b; 以下将使用sqflite作为例子&#xff0c;sqflite允许在 Flutter 应用程序中执行 SQL 查询&#xff0c;创…...

编程日记 2024/1/15 6:36:50

docker应用：搭建uptime-kuma监控站点

简介&#xff1a;Uptime Kuma是一个易于使用的自托管监控工具&#xff0c;它的界面干净简洁&#xff0c;部署和使用都非常方便。 历史攻略&#xff1a; docker&#xff1a;可视化工具portainer docker-compose&#xff1a;搭建自动化运维平台Spug 开源地址&#xff1a; ht…...

编程日记 2024/1/15 6:35:50

在illustrator中按大小尺寸选择物体 ＜脚本 018＞

在Illustrator中我们可以依据对象的属性 如&#xff1a;填充颜色、描边颜色或描边宽度来选择相同属性的对象&#xff0c;但是Illustrator中没有根据不同大小尺寸来选择对象的功能&#xff0c;下面介绍的就是根据大小尺寸选择对象的脚本。 1、下面是当前画板中的所有对象&#…...

编程日记 2024/1/15 6:33:48

leetcode - 934. Shortest Bridge

Description You are given an n x n binary matrix grid where 1 represents land and 0 represents water. An island is a 4-directionally connected group of 1’s not connected to any other 1’s. There are exactly two islands in grid. You may change 0’s to 1…...

编程日记 2024/1/15 6:32:47

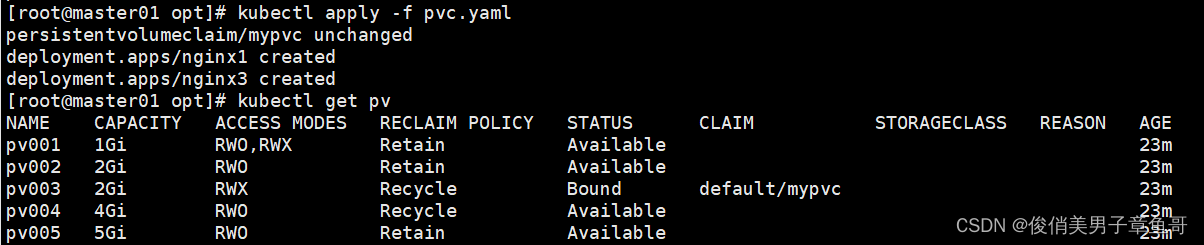
k8s的存储卷、数据卷

容器内的目录和宿主机目录进行挂载。 容器在系统上的生命周期是短暂的。 k8s用控制器创建的pod。delete相当于重启。容器的状态也会恢复到初始状态。一旦恢复到初始状态&#xff0c;所有的后天编辑的文件都会消失 容器和节点之间创建一个可以持久化保存容器内文件的存储卷。…...

编程日记 2024/1/15 6:31:46

流星全自动网页生成系统重构版源码

流星全自动网页生成系统重构版源码分享&#xff0c;所有模板经过精心审核与修改&#xff0c;完美兼容小屏手机大屏手机&#xff0c;以及各种平板端、电脑端和360浏览器、谷歌浏览器、火狐浏览器等等各大浏览器显示。 为用户使用方便考虑&#xff0c;全自动网页制作系统无需繁琐…...

编程日记 2024/1/15 6:28:44

vscode打开c_cpp_properties.json文件的一种方式

步骤一 点击win32 步骤二 点击json 自动生成了...

编程日记 2024/1/15 6:26:42

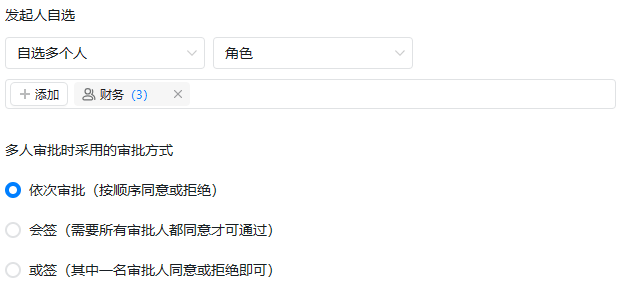
发起人自选-钉钉审批

场景描述 配置一个审批流程&#xff0c;在某些审批节点&#xff0c;不能确定谁具体来审批&#xff0c;所以需要手工选择一个人或者多个人保证流程能得以顺利通过。有些审批流程的做法是&#xff0c;上一个节点来选择指定的人&#xff0c;而钉钉的做法是发起人来指定。 钉钉设…...

编程日记 2024/1/15 6:22:39

电脑DIY-显卡

显卡 英伟达&#xff08;NVIDIA&#xff09;RTX系列 英伟达&#xff08;NVIDIA&#xff09; 英伟达&#xff08;NVIDIA&#xff09;是一家知名的图形处理器制造商&#xff0c;其显卡产品系列众多。以下是英伟达显卡的主要系列&#xff1a; 系列面向客户说明产品GeForce系列个…...

编程日记 2024/1/15 6:21:38

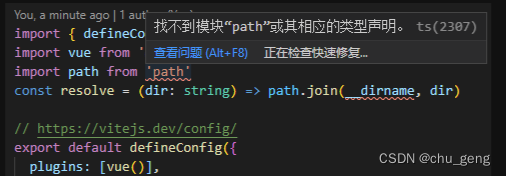
vue3+vite+ts+pinia新建项目（略详细版）

1、新建项目 npm create vite@latest 2、安装依赖 yarn add vue-router yarn add -D @types/node vite-plugin-pages sass sass-loader 3、配置别名 //vite.config.ts import { defineConfig } from vite import path from node:path export default defineConfig({ plu…...

编程日记 2024/1/15 6:16:31

（二）TensorRT-LLM | 模型导出（v0.20.0rc3）

0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述&#xff0c;后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作&#xff0c;其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

编程新知 2025/11/2 16:08:18

vue3 字体颜色设置的多种方式

在Vue 3中设置字体颜色可以通过多种方式实现&#xff0c;这取决于你是想在组件内部直接设置&#xff0c;还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法&#xff1a; 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

编程新知 2025/10/6 20:49:11

Cinnamon修改面板小工具图标

Cinnamon开始菜单-CSDN博客 设置模块都是做好的&#xff0c;比GNOME简单得多&#xff01; 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

编程新知 2025/11/3 22:44:34

生成 Git SSH 证书

&#x1f511; 1. ​​生成 SSH 密钥对​​ 在终端&#xff08;Windows 使用 Git Bash&#xff0c;Mac/Linux 使用 Terminal&#xff09;执行命令&#xff1a; ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" ​​参数说明​​&#xff1a; -t rsa&#x…...

编程新知 2025/9/18 11:31:13

Cloudflare 从 Nginx 到 Pingora：性能、效率与安全的全面升级

在互联网的快速发展中&#xff0c;高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司&#xff0c;近期做出了一个重大技术决策&#xff1a;弃用长期使用的 Nginx&#xff0c;转而采用其内部开发…...

编程新知 2025/10/26 5:13:27

Rapidio门铃消息FIFO溢出机制

关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系&#xff0c;以下是深入解析&#xff1a; 门铃FIFO溢出的本质 在RapidIO系统中&#xff0c;门铃消息FIFO是硬件控制器内部的缓冲区&#xff0c;用于临时存储接收到的门铃消息&#xff08;Doorbell Message&#xff09;。…...

编程新知 2025/11/2 0:32:25

均衡后的SNRSINR

本文主要摘自参考文献中的前两篇&#xff0c;相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程&#xff0c;其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt​ 根发送天线&#xff0c; n r n_r nr​ 根接收天线的 MIMO 系…...

编程新知 2025/11/2 20:33:45

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理）

上一章用到了V2 的概念&#xff0c;其实 Fiori当中还有 V4&#xff0c;咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务)&#xff0c;代理中间件&#xff08;ui5-middleware-simpleproxy&#xff09;-CSDN博客…...

编程新知 2025/11/3 20:51:50

MySQL 知识小结（一）

一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库&#xff0c;分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷&#xff0c;但是文件存放起来数据比较冗余&#xff0c;用二进制能够更好管理咱们M…...

编程新知 2025/10/28 3:27:57

C++ 设计模式 《小明的奶茶加料风波》

&#x1f468;‍&#x1f393; 模式名称&#xff1a;装饰器模式&#xff08;Decorator Pattern&#xff09; &#x1f466; 小明最近上线了校园奶茶配送功能&#xff0c;业务火爆&#xff0c;大家都在加料&#xff1a; 有的同学要加波霸 &#x1f7e4;&#xff0c;有的要加椰果…...

编程新知 2025/11/2 13:18:58