opencv通过轮廓点生成闭合图像
前言
有时候需要将某一些点生成闭合的二值图像。记录一下。
// 轮廓点个数
int nrCurvePoints = curContour.nr;
// 轮廓点
DIM2DL* curvePoints = curContour.pts;std::vector<cv::Point> points; // 轮廓点集合
for (int cntPoint = 0; cntPoint < nrCurvePoints; ++cntPoint)
{int x = curvePoints[cntPoint].x;int y = curvePoints[cntPoint].y;points.emplace_back(cv::Point(x, y));
}// 轮廓点转Mat
cv::Mat contourImg = cv::Mat::zeros(cv::Size(usW, usH), CV_8UC1);
std::vector<std::vector<cv::Point>> contoursCV;
contoursCV.push_back(points);
cv::fillPoly(contourImg, contoursCV, cv::Scalar(255));// 保存至io文件夹
std::string savePath(str_ws_US + "io/inContour_flag" + std::to_string(curFlag) + "_index" + std::to_string(index) + ".jpg");
cv::imwrite(savePath, contourImg);
相关文章:

opencv通过轮廓点生成闭合图像
前言 有时候需要将某一些点生成闭合的二值图像。记录一下。 // 轮廓点个数 int nrCurvePoints curContour.nr; // 轮廓点 DIM2DL* curvePoints curContour.pts;std::vector<cv::Point> points; // 轮廓点集合 for (int cntPoint 0; cntPoint < nrCurvePoints; cn…...
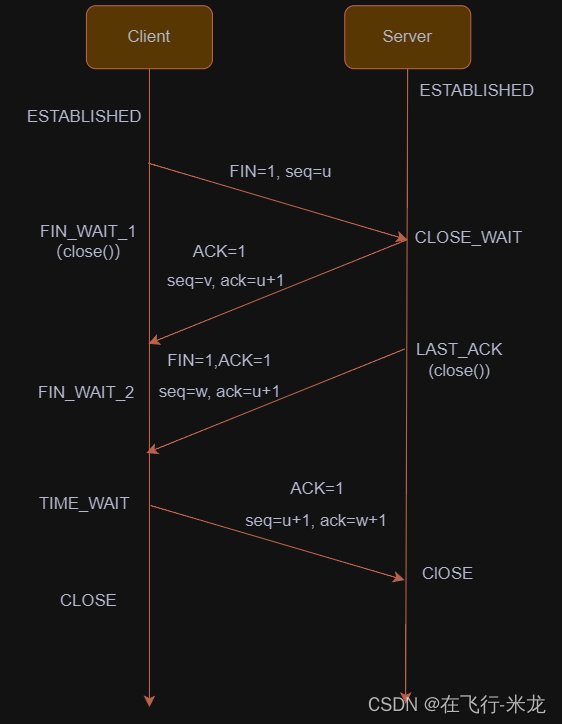
Python 网络编程之TCP详细讲解
【一】传输层 【1】概念 传输层是OSI五层模型中的第四层,负责在网络中的两个端系统之间提供数据传输服务主要协议包括**TCP(传输控制协议)和UDP(用户数据报协议)** 【2】功能 **端到端通信:**传输层负责…...

直饮水系统服务认证:提升水质与安全的必要举
直饮水系统作为一种便捷、卫生的饮水方式,已经越来越受到人们的欢迎。然而,随着市场的发展,直饮水系统的质量和服务也面临着一些挑战。因此,直饮水系统服务认证应运而生,成为了提升水质与安全的必要举措。 一、直饮水…...
Qt 调试系统输出报警声以及添加资源
文章目录 前言一、方法1 使用 Qsound1.添加都文件 直接报错2.解决这个错误 添加 QT multimedia3. 加入代码又遇到新的错误小结 二、第二种方法1.引入库2.添加资源2.1依次点击Qt--->Qt Resource File--->Choose2.2给资源文件起个名字,如:res&#…...
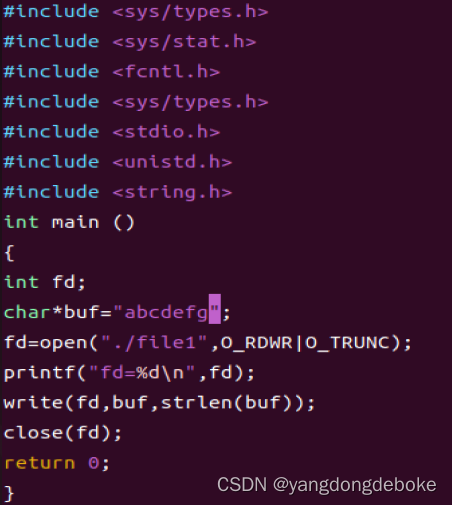
Linux下文件的创建写入读取编程
在linux下操作一个文件,首先要保证文件的存在(不存在就创建),接着打开文件(打开成功)并得到文件描述符,接着在进行读写操作,最后还需要关闭文件。如果我们对文件进行读写之后不关闭文…...

python 解析
list(pd.DataFrame) # 所有列名切片:print("显式 切片:\n", df.loc[:, "number":"sum"]) 所有行,列是从number 到sum ,前闭后开print("隐式 切片:\n", df.iloc[:, 1:3]) # 结果和上面一样转化成字典…...
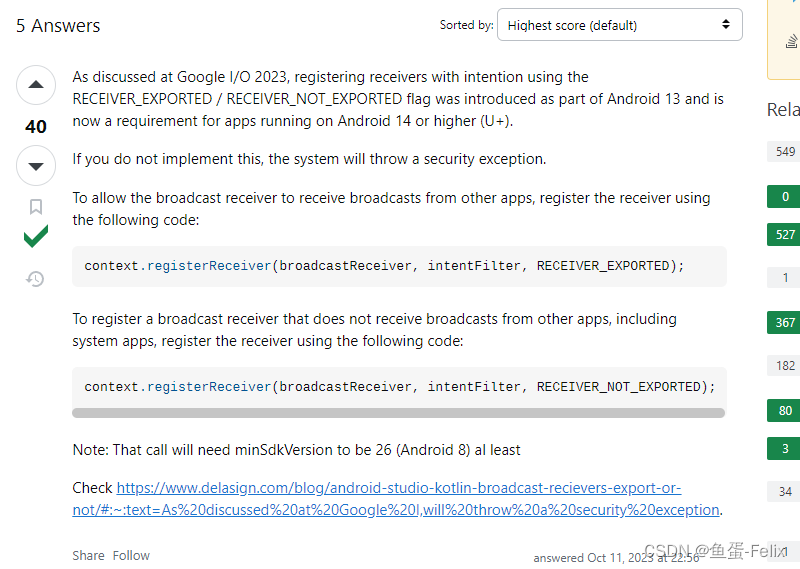
谷歌aab包在Android 14闪退而apk没问题(targetsdk 34)
问题原因 Unity应用(target SDK 34)上线到GooglePlay,有用户反馈fold5设备上(Android14系统)疯狂闪退,经测试,在小米手机Android14系统的版本复现成功了,奇怪的是apk直接安装没问题,而打包成aa…...

34.在排序数组中查找元素的第一个和最后一个位置
34.在排序数组中查找元素的第一个和最后一个位置 给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1, -1]。 你必须设计并实现时间复杂度为…...

js树过滤
// 递归过滤得到每一项的hidden为false的数据 function filterTree(arr) { return arr.filter(item > { if (item.children) { item.children filterTree(item.children) } if (!item.hidden) { return true } }) }...

Java多线程并发篇----第十六篇
系列文章目录 文章目录 系列文章目录前言一、线程等待(wait)二、线程睡眠(sleep)三、线程让步(yield)四、线程中断(interrupt)五、Join 等待其他线程终止前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这…...

测评结果:免费的“文心一言3.5”香,但是付费的产品质量更高
文章目录 前言一、文心一言3.5生成的图片和文章1.文心一言生成的图片在文心一言3.5中输入以下内容:我的测评结果: 2.文心一言生成的文章在文心一言3.5中输入以下内容:我的测评结果: 二、ChatGPT生成的图片和文章1.ChatGPT4.0 生成…...
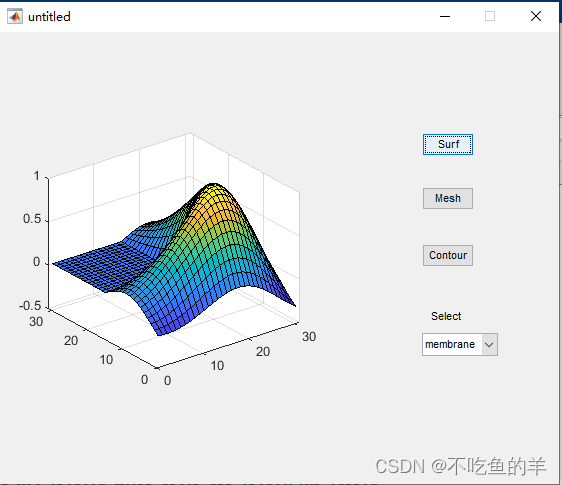
Matlab GUI设计基础范例(可以一步一步跟着做)
我们要做一个GUI界面,可以选择peaks、membrane和sinc三种三维图数据,选择画出surf、mesh和contour三种图像。 打开GUI 每个版本打开方式可能都不一样,但有一个是相同的,就是在命令行输入guide回车。 绘制控件 大概就绘制成这样…...
与 @Transactional区别)
@Transactional(rollbackFor = {Exception.class})与 @Transactional区别
在Spring框架中,Transactional 注解用于标记方法或类,以表明该方法或类内包含的数据库操作应当在一个事务中执行。事务的基本原则是“原子性”,即所有操作要么全部成功,要么全部失败。 1. Transactional(不指定 rollb…...

数据结构——二叉树(先序、中序、后序及层次四种遍历(C语言版))超详细~ (✧∇✧) Q_Q
目录 二叉树的定义: *特殊的二叉树: 二叉树的性质: 二叉树的声明: 二叉树的先序遍历: 二叉树的中序遍历: 二叉树的后序遍历: 二叉树的层序遍历: 二叉树的节点个数: 二叉…...
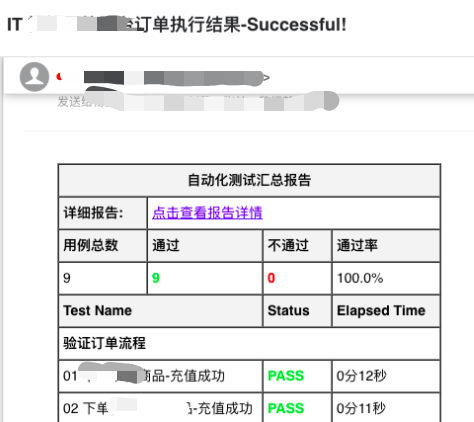
如何快速打造属于自己的接口自动化测试框架
1 接口测试 接口测试是对系统或组件之间的接口进行测试,主要是校验数据的交换,传递和控制管理过程,以及相互逻辑依赖关系。 接口自动化相对于UI自动化来说,属于更底层的测试,这样带来的好处就是测试收益更大ÿ…...

人工智能在数据安全中的应用场景
场景一:数据资产梳理 数据资产梳理是数据安全的基础。知道企业究竟有多少数据,这些数据在哪里?有哪些类型的数据?其中哪些是敏感数据?这些数据的敏感等级分别是什么?只有明确了保护的目标,才能…...

2024.1.16每日一题
LeetCode 2719.统计整数数目 2719. 统计整数数目 - 力扣(LeetCode) 题目描述 给你两个数字字符串 num1 和 num2 ,以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件,我们称它是一个好整数: num1 &l…...
python入门,数据容器的通用操作(len,max,min,sorted)
1.len统计容器内元素个数 2.max统计元素最大元素 3.min统计元素最小元素 4.容器的转化功能 list(容器)将给定容器转化为列表 字符串转列表将字符串内的每一个元素都取了出来作为列表的每一个元素 字典则只会取出它的key,value会消失 str&…...
运筹说 第67期 | 动态规划模型的建立与求解
通过前一期的学习,我们已经学会了动态规划的基本概念和基本原理。本期小编带大家学习动态规划模型的建立与求解。 动态规划模型的建立 一 概述 建立动态规划的模型,就是分析问题并建立问题的动态规划基本方程。 成功地应用动态规划方法的关键&#x…...

大模型压缩与优化的技术原理与创新方法
目录 前言1 模型压缩简介2 知识蒸馏3 模型剪枝3.1 结构化剪枝3.2 非结构化剪枝 4 模型量化4.1 浮点表示 vs 定点表示4.2 位数选择与性能影响4.3 量化技术 5 其他模型压缩方法5.1 Weight Sharing: 参数共享5.2 Low-rank Approximation: 低秩分解5.3 Architecture Search: 神经网…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
