<蓝桥杯软件赛>零基础备赛20周--第14周--BFS
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集
20周的完整安排请点击:20周计划
每周发1个博客,共20周。
在QQ群上交流答疑:

文章目录
- 1. BFS简介和基本代码
- 2. BFS与最短路径
- 2.1 计算最短路的长度
- 2.2 输出完整的最短路径
- 3. BFS与判重
- 3.1 C++判重
- 3.2 Java判重
- 3.3 Python判重
第14周: BFS
1. BFS简介和基本代码
第12周博客用“一群老鼠走迷宫”做比喻介绍了BFS的原理,类似的比喻还有“多米诺骨牌”、“野火蔓延”。BFS的搜索过程是由近及远的,从最近的开始,一层层到达最远处。以下面的二叉树为例,一层一层地访问,从A出发,下一步访问B、C,再下一步访问D、E、F、G,最后访问H、I。圆圈旁边的数字是访问顺序。
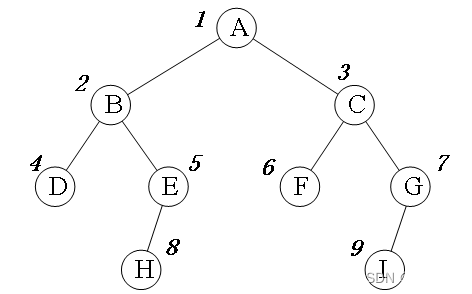
一句话概况BFS的思想:全面扩散、逐层递进。
BFS的逐层访问过程如何编程实现?非常简单,用队列,“BFS = 队列”。队列的特征是先进先出,并且不能插队。BFS用队列实现:第一层先进队列,然后第二层进队列、第三层、…。
上面图示的二叉树用队列进行BFS操作:根节点A第1个进队列;然后让A的子节点B、C进队列;接下来让B、C的子节点D、E、F、G进队列;最后让E、G的子节点H、I进队列。节点进入队列的先后顺序是A-BC-DEFG-HI,正好按层次分开了。
在任何时刻,队列中只有相邻两层的点。
下面的代码输出图示二叉树的BFS序,用队列实现。队列和二叉树参考第6周队列和第7周二叉树的讲解。
C++代码
#include <bits/stdc++.h>
using namespace std;
const int N=100;
char t[N]; //简单地用一个数组定义二叉树
int ls(int p){return p<<1;} //定位左孩子,也可以写成 p*2
int rs(int p){return p<<1 | 1;} //定位右孩子,也可以写成 p*2+1
void bfs(int root) {queue<int> q; //定义队列q.push(root); //第一个节点进入队列while (!q.empty()) { //用BFS访问二叉树int u = q.front(); //读队头,并输出cout << t[u];q.pop(); //队头处理完了,弹走if (t[ls(u)]) q.push(ls(u)); //左儿子进队列if (t[rs(u)]) q.push(rs(u)); //右儿子进队列}
}
int main(){t[1]='A'; //第1层t[2]='B'; t[3]='C'; //第2层t[4]='D'; t[5]='E'; t[6]='F'; t[7]='G'; //第3层t[10]='H'; t[14]='I'; //第4层bfs(1); //BFS访问二叉树,从根节点1开始。输出:ABCDEFGHIcout<<"\n";bfs(3); //BFS访问二叉树的子树,从子节点3开始。输出:CFGIreturn 0;
}
Java代码
import java.util.*;
public class Main {private static final int N = 100;private static char[] t = new char[N]; //简单地用一个数组定义二叉树private static int ls(int p) {return p<<1;} //定位左孩子,也可以写成 p*2private static int rs(int p) {return (p<<1) | 1;} //定位右孩子,也可以写成 p*2+1private static void bfs(int root) {Queue<Integer> queue = new LinkedList<>(); //定义队列queue.add(root); //第一个节点进入队列while (!queue.isEmpty()) { //用BFS访问二叉树int u = queue.peek(); //读队头,并输出System.out.print(t[u]);queue.poll(); //队头处理完了,弹走if (t[ls(u)] != '\0') queue.add(ls(u)); //左儿子进队列 if (t[rs(u)] != '\0') queue.add(rs(u)); //右儿子进队列 }}public static void main(String[] args) {t[1] = 'A'; //第1层t[2] = 'B'; t[3] = 'C'; //第2层t[4] = 'D'; t[5] = 'E'; t[6] = 'F'; t[7] = 'G'; //第3层t[10] = 'H'; t[14] = 'I'; //第4层bfs(1); //BFS访问二叉树,从根节点1开始。输出:ABCDEFGHISystem.out.println();bfs(3); //BFS访问二叉树的子树,从子节点3开始。输出:CFGI}
}
Python代码
from collections import deque
N = 100
t = [''] * N # 简单地用一个数组定义二叉树
def ls(p): return p << 1 # 定位左孩子,也可以写成 p*2
def rs(p): return (p << 1) | 1 # 定位右孩子,也可以写成 p*2+1
def bfs(root): q = deque() # 定义队列q.append(root) # 第一个节点进入队列while q: # 用BFS访问二叉树u = q.popleft() # 读队头,并弹走print(t[u], end='') # 输出队头if t[ls(u)]: q.append(ls(u)) # 左儿子进队列 if t[rs(u)]: q.append(rs(u)) # 右儿子进队列
t[1] = 'A' # 第1层
t[2] = 'B'; t[3] = 'C' # 第2层
t[4] = 'D'; t[5] = 'E'; t[6] = 'F'; t[7] = 'G' # 第3层
t[10] = 'H';t[14] = 'I' # 第4层
bfs(1) # BFS访问二叉树,从根节点1开始。输出:ABCDEFGHI
print()
bfs(3) # BFS访问二叉树的子树,从子节点3开始。输出:CFGI
2. BFS与最短路径
求最短路径是BFS最常见的应用。
BFS本质上就是一个最短路径算法,因为它由进及远访问节点,先访问到的节点,肯定比后访问到的节点更近。某个节点第一次被访问到的时候,必定是从最短路径走过来的。从起点出发,同一层的节点,到起点的距离都相等。
不过,BFS求最短路有个前提:任意两个邻居节点的边长都相等,把两个邻居节点之间的边长距离称为“一跳”。只有所有边长都相等,才能用BFS的逐层递进来求得最短路。两个节点之间的路径长度,等于这条路径上的边长个数。在这种场景下,BFS是最优的最短路算法,它的计算复杂度只有O(n+m),n是节点数,m是边数。如果边长都不等,就不能用BFS求最短路了,路径长度也不能简单地用边长个数来统计。
下图中,A到B、C、D的最短路长度都是1跳,A到E、F、G、H的最短路都是2跳。
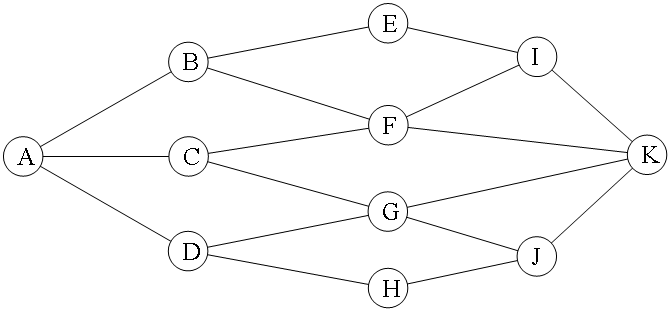
用BFS求最短路路径的题目一般有两个目标:
(1)最短路径的长度。答案唯一,路径长度就是路径经过的边长数量。
(2)最短路径具体经过哪些节点。由于最短路径可能有多条,所以一般不用输出最短路径。如果要输出,一般是输出字典序最小的那条路径。例如上图中,A到F的最短路有两条:A-B-F、A-C-F,字典序最小的是A-B-F。
BFS最短路径的常用的场景是网格图,下面给出一道例题,用这道例题说明如何计算最短路、如何输出路径。
2.1 计算最短路的长度
例题:马的遍历
马走日,从一个坐标点出发,下一步有8种走法。第4、5行用dx[]、dy[]定义下一步的8个方向。设左上角的坐标是(1,1),右下角坐标是(n,m)。
代码的主体部分是标准的BFS,让每个点进出队列。注意如何用队列处理坐标。第24行定义队列,队列元素是坐标struct node。
用dis[][]记录最短路径长度,dis[x][y]是从起点s到(x,y)的最短路径长度。第35行,每扩散一层,路径长度就加1。
C++代码:
#include <bits/stdc++.h>
using namespace std;
struct node{int x,y;}; //定义坐标。左上角(1,1),右下角(n,m)
const int dx[8]={2,1,-1,-2,-2,-1, 1, 2}; //8个方向,按顺时针
const int dy[8]={1,2, 2, 1,-1,-2,-2,-1};
int dis[500][500]; //dis[x][y]: 起点到(x,y)的最短距离长度
int vis[500][500]; //vis[x][y]=1: 已算出起点到坐标(x,y)的最短路
node pre[500][500]; //pre[x][y]:坐标(x,y)的前驱点
void print_path(node s, node t){ //打印路径:从起点s到终点tif(t.x==s.x && t.y==s.y) { //递归到了起点printf("(%d,%d)->",s.x,s.y); //打印起点,返回return;}node p;p.x = pre[t.x][t.y].x; p.y = pre[t.x][t.y].y;print_path(s,p); //先递归回到起点printf("(%d,%d)->",t.x,t.y); //在回溯过程中打印,最后打的是终点
}
int main(){int n,m; node s; cin>>n>>m>>s.x>>s.y;memset(dis,-1,sizeof(dis));dis[s.x][s.y]=0; //起点到自己的距离是0vis[s.x][s.y]=1;queue<node> q;q.push(s); //起点进队while(!q.empty()){node now = q.front();q.pop(); //取队首并出队for(int i=0;i<8;i++) { //下一步可以走8个方向node next;next.x=now.x+dx[i],next.y=now.y+dy[i];if(next.x<1||next.x>n||next.y<1||next.y>m||vis[next.x][next.y])continue; //出界或已经走过vis[next.x][next.y]=1; //标记为已找到最短路dis[next.x][next.y]=dis[now.x][now.y]+1; //计算最短路长度pre[next.x][next.y] = now; //记录点next的前驱是nowq.push(next); //进队列}}for(int i=1;i<=n;i++) {for(int j=1;j<=m;j++)printf("%-5d",dis[i][j]);printf("\n");}// node test; test.x=3; test.y=3; //测试路径打印,样例输入:3 3 1 1,终点(3,3)// print_path(s,test); //输出路径:(1,1)->(3,2)->(1,3)->(2,1)->(3,3)->return 0;
}
2.2 输出完整的最短路径
本题没有要求打印出具体的路径,不过为了演示如何打印路径,代码中加入了函数print_path(s,t),打印从起点s到终点t的完整路径。第47行打印起点s=(1,1),终点t=(3,3)的完整路径:(1,1)->(3,2)->(1,3)->(2,1)->(3,3)。如下图虚线箭头所示。

如何记录一条路径?在图上从一个起点s出发做一次BFS,可以求s到其他所有点的最短路。为了记录路径,最简单的方法是每走到一个点i,就在i上把从起点s到i经过的所有点都记下来。例如上图,从(1,1)出发,下一步可以走到(3,2),就在(3,2)上记录”(1,1)->(3,2)”;再走一步可以到(1,3),就在(1,3)上接着记录“(1,1)->(3,2)->(1,3)”;再走一步到(2,1),就在(2,1)上记录“(1,1)->(3,2)->(1,3)->(2,1)”。这样做编程简单,但是浪费空间,因为每个点上都要记录从头到尾的完整路径。
《算法竞赛》123页“3.4 BFS与最短路径”介绍了这两种路径记录方法:简单方法、标准方法。
标准的路径记录方法是:只在点i上记录前驱点,也就是从哪个点走到i的。例如点(1,3),记录它的前驱点是(3,2),(3,2)记录它的前驱点是(1,1)。当需要输出起点(1,1)到(1,3)的完整路径时,只需要从(3,2)倒查回去,就能得到完整路径了。这样做非常节省空间,一个点上只需要记录前一个点就行了。
为什么不在点i上记录它的下一个点?请读者自己思考。
代码第8行用node pre[][]记录路径,pre[x][y]记录了坐标(x,y)的前驱点。按照pre[][]的记录倒查路径上每个点的前一个点,一直查到起点,就得到了完整路径。例如上图,终点为(3,3),pre[3][3]是它的上一个点(2,1);(2,1)的pre[2][1]是它的上一个点(1,3);(1,3)的上一个点是(3,2);(3,2)的上一个点是(1,1),回到了起点。
print_path()打印路径,它是一个递归函数,从终点开始倒查pre[][],一直递归到起点,然后再回溯回终点。在回溯的过程中从起点开始打印路径上的点,就得到了从起点到终点的正序路径。
另外,从起点s到终点t可能有多条最短路径,上面的代码只记录了按顺时针的优先顺序找到的第一条最短路径。第4、5行的dx[]、dy[]按顺时针定义了8个方向,然后在第29行遍历邻居时,也是按dx[]、dy[]的顺序,那么得到的最短路径就是按顺时针的。
Java代码:
import java.util.*;
class Main {static class Node { //定义坐标。左上角(1,1),右下角(n,m)int x, y;Node(int x, int y) {this.x = x;this.y = y;}}public static void printPath(Node s, Node t, Node[][] pre){ //打印路径:起点s终点tif (t.x == s.x && t.y == s.y) { //递归到了起点System.out.print("(" + s.x + "," + s.y + ")->"); //打印起点,然会回溯return;}Node p = pre[t.x][t.y];printPath(s, p, pre); //先递归回到起点System.out.print("(" + t.x + "," + t.y + ")->"); //回溯打印,最后打的是终点}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();Node s = new Node(scanner.nextInt(), scanner.nextInt());int[][] dis = new int[n+1][m+1]; //dis[x][y]:起点到(x,y)的最短距离长度int[][] vis = new int[n+1][m+1]; //vis[x][y]=1:已算出起点到坐标(x,y)的最短路Node[][] pre = new Node[n + 1][m + 1]; //pre[x][y]:坐标(x,y)的前驱点int[] dx = {2, 1, -1, -2, -2, -1, 1, 2}; //8个方向,按顺时针int[] dy = {1, 2, 2, 1, -1, -2, -2, -1};for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)dis[i][j] = -1;dis[s.x][s.y] = 0; //起点到自己的距离是0vis[s.x][s.y] = 1;Queue<Node> queue = new LinkedList<>();queue.add(s); //起点进队while (!queue.isEmpty()) {Node now = queue.poll(); //取队首并出队for (int i = 0; i < 8; i++) {int nx = now.x + dx[i];int ny = now.y + dy[i];if (nx < 1 || nx > n || ny < 1 || ny > m || vis[nx][ny] == 1) continue; //出界或已经走过vis[nx][ny] = 1; //标记为已找到最短路dis[nx][ny] = dis[now.x][now.y] + 1; //计算最短路长度pre[nx][ny] = now; //记录点next的前驱是nowqueue.add(new Node(nx, ny));//进队列}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) System.out.printf("%-5d", dis[i][j]); System.out.println();}// Node test = new Node(3, 3); //测试路径打印,样例输入:3 3 1 1,终点(3,3)// printPath(s, test, pre); //输出路径:(1,1)->(3,2)->(1,3)->(2,1)->(3,3)->}
}
Python代码
from collections import deque
dx = [2, 1, -1, -2, -2, -1, 1, 2] #8个方向,按顺时针
dy = [1, 2, 2, 1, -1, -2, -2, -1]
class Node: #定义坐标。左上角(1,1),右下角(n,m)def __init__(self, x, y):self.x = xself.y = y
def print_path(s, t, pre): #打印路径:从起点s到终点tif t.x == s.x and t.y == s.y: #递归到了起点print(f"({s.x},{s.y})->", end="") #打印起点,返回returnp = pre[t.x][t.y] print_path(s, p, pre) #先递归回到起点print(f"({t.x},{t.y})->", end="") #在回溯过程中打印,最后打的是终点
def main():n, m,u,v = map(int, input().split())s = Node(u,v)dis = [[-1] * (m+1) for _ in range(n+1)] #dis[x][y]: 起点到(x,y)的最短距离长度vis = [[0] * (m+1) for _ in range(n+1)] #vis[x][y]=1: 已算出起点到(x,y)的最短路pre = [[None] * (m+1) for _ in range(n+1)] #pre[x][y]: 坐标(x,y)的前驱点dis[s.x][s.y] = 0 #起点到自己的距离是0vis[s.x][s.y] = 1q = deque([s]) #起点进队while q: now = q.popleft() #取队首并出队for i in range(8): #下一步可以走8个方向nx, ny = now.x + dx[i], now.y + dy[i]if nx<1 or nx>n or ny < 1 or ny > m or vis[nx][ny]:continue #出界或已经走过vis[nx][ny] = 1 #标记为已找到最短路dis[nx][ny] = dis[now.x][now.y] + 1 #计算最短路长度pre[nx][ny] = now #记录点(nx,ny)的前驱是nowq.append(Node(nx, ny)) #进队列for i in range(1, n + 1):for j in range(1, m + 1):print(f"{dis[i][j]:-5d}", end="")print() #test = Node(3, 3) #测试路径打印,样例输入:3 3 1 1,终点(3,3)#print_path(s, test, pre) #输出路径:(1,1)->(3,2)->(1,3)->(2,1)->(3,3)->
if __name__ == "__main__":main()
3. BFS与判重
BFS的题目往往需要“判重”。BFS的原理是逐层扩展,把扩展出的下一层点(或称为状态)放进队列中。
在任意时刻,队列中只包含相邻两层的点。只有两层,看起来似乎不多,但是很多情况下是个极大的数字。例如一棵满二叉树,第25层的点就有225≈3000万个,队列放不下。
不过在很多情况下,其实状态的总数量并不多,在层层扩展过程中,很多状态是重复的,没有必要重新放进队列。这产生了判重的需求。
用下面的题目说明判重的原理和编程方法。
例题:九宫重排
题目求从初态到终态的最少步数,是典型的BFS最短路路径问题。
让卡片移动到空格比较麻烦,改为让空格上下左右移动,就简单多了。空格的每一步移动,可能有2、3、4种新局面,如果按3种算,移动到第15步,就有315>1千万种局面,显然队列放不下。不过,其实局面总数仅有9!=362880种,队列放得下,只要判重,不让重复的局面进入队列即可。
3.1 C++判重
判重可以用STL map或set。(1)map判重。map是STL容器,存放键值对。键有唯一性,键和值有一一对应关系。由于每个键是独一无二的,可以用来判重。map的基本用法见下面的例子。
#include <bits/stdc++.h>
using namespace std;
int main(){map<string,int> mp{{"tom",78},{"john",92},{"rose",83}}; //三个键值对cout << mp["tom"]<<"\n"; //输出 78cout << mp.count("tom")<<"\n"; //检查map中是否有"tom"。输出 1mp["white"]=100; //加入新键值对,键是"white",值是100cout << mp["white"]<<"\n"; //输出 100cout << mp.count("sam")<<"\n"; //查不到键,输出 0map<int, int> mp2{{2301,89},{2302,98}}; cout << mp2[2301]<<"\n"; //输出 89map<int, string> mp3{{301,"dog"},{232,"pig"}};cout << mp3[232]<<"\n"; //输出 pigreturn 0;
}
map容器中提供了count()用于统计键的个数,有键返回1,没有键返回0。count()可以用来判重:若某个键的count()等于1,说明这个键已经在map中,不用再放进map。
下面给出本题的C++代码。第22行判重,判断局面tmp是否曾经处理过,第23行把新局面tmp放进map。
#include <bits/stdc++.h>
using namespace std;
int dx[] = {-1, 0, 1, 0}; //上下左右四个方向
int dy[] = { 0, 1, 0, -1};
map <string,int> mp;
int bfs(string s1,string s2){queue<string>q;q.push(s1);mp[s1]=0; //mp[s1]=0表示s1到s1的步数是0。另外:mp.count(s1)=1while(q.size()){string ss = q.front();q.pop();int dist = mp[ss]; //从s1到ss的移动步数if(ss==s2) return dist; //到达终点,返回步数int k=ss.find('.'); //句点的位置int x=k/3,y=k%3; //句点坐标:第x行、第y列for(int i=0;i<4;i++){int nx=x+dx[i], ny=y+dy[i]; //让句点上下左右移动if(nx<0 || ny<0 || nx>2 || ny>2) continue; //越界string tmp=ss;swap(tmp[k],tmp[nx*3+ny]); //移动if(mp.count(tmp)==0){ //判重,如果tmp曾经处理过,就不再处理mp[tmp] = dist+1; //把tmp放进map,并赋值。mp[tmp]等于s1到tmp的步数q.push(tmp);}}}return -1; //没有找到终态局面,返回-1
}
int main(){string s1,s2; cin>>s1>>s2; //初态局面s1,终态局面s2cout<<bfs(s1,s2);return 0;
}
(2)set判重。set是STL的常用容器,set中的元素是有序的且具有唯一性,利用这个特性,set常用来判重。set的基本用法见下面的例子。
#include <bits/stdc++.h>
using namespace std;
int main() {set<string>st{"111","222","33"}; // 定义 set,插入初值if(st.count("111")) cout <<1; //有"111",输出 1else cout <<-1;cout<<"\n";if(st.count("44")) cout <<4;else cout <<-4; //无"44",输出 -4cout <<"\n";st.insert("44"); //插入"44"if(st.count("44")) cout <<4; //有"44",输出 4return 0;
}
本题用set判重的代码:
#include <bits/stdc++.h>
using namespace std;
int dx[] = {-1, 0, 1, 0}; //上下左右四个方向
int dy[] = { 0, 1, 0, -1};
struct node{node(string ss, int tt){s=ss, t=tt;}string s; //局面int t; //到这个局面的步数
};
set <string> st; //用set st判重
int bfs(string s1,string s2){queue<node>q;q.push(node(s1,0));st.insert(s1);while(q.size()){node now = q.front();q.pop();string ss = now.s;int dist = now.t; //从s1到ss的移动步数if(ss==s2) return dist; //到达终点,返回步数int k=ss.find('.'); //句点的位置int x=k/3,y=k%3; //句点坐标:第x行、第y列for(int i=0;i<4;i++){int nx=x+dx[i], ny=y+dy[i]; //让句点上下左右移动if(nx<0 || ny<0 || nx>2 || ny>2) continue; //越界string tmp=ss;swap(tmp[k],tmp[nx*3+ny]); //移动if(st.count(tmp)==0){ //判重,如果tmp曾经处理过,就不再处理st.insert(tmp);q.push(node(tmp,dist+1));}}}return -1; //没有找到终态局面,返回-1
}
int main(){string s1,s2; cin>>s1>>s2; //初态局面s1,终态局面s2cout<<bfs(s1,s2);return 0;
}
3.2 Java判重
(1)用map判重
import java.util.*;
public class Main {static int[] dx = {-1, 0, 1, 0}; // 上下左右四个方向static int[] dy = {0, 1, 0, -1};static Map<String, Integer> mp;public static int bfs(String s1, String s2) {Queue<String> q = new LinkedList<>();q.add(s1);mp.put(s1, 0); // 0表示s1到s1的步数是0while (!q.isEmpty()) {String ss = q.poll();int dist = mp.get(ss); // 从s1到ss的移动步数if (ss.equals(s2)) return dist; // 到达终点,返回步数int k = ss.indexOf('.'); // 句点的位置int x = k / 3, y = k % 3; // 句点坐标:第x行、第y列for (int i = 0; i < 4; i++) {int nx = x + dx[i], ny = y + dy[i]; // 让句点上下左右移动if (nx < 0 || ny < 0 || nx > 2 || ny > 2) continue; // 越界StringBuilder tmp = new StringBuilder(ss);tmp.setCharAt(k, tmp.charAt(nx * 3 + ny)); // 移动tmp.setCharAt(nx * 3 + ny, '.');if (!mp.containsKey(tmp.toString())) {//判重,如果tmp处理过,就不再处理mp.put(tmp.toString(), dist + 1); //把tmp放进map,并赋值为步数q.add(tmp.toString());}}}return -1; // 没有找到终态局面,返回-1}public static void main(String[] args) {mp = new HashMap<>();Scanner scanner = new Scanner(System.in);String s1 = scanner.next();String s2 = scanner.next();System.out.println(bfs(s1, s2));}
}
(2)用set判重
import java.util.*;
public class Main {static int[] dx = {-1, 0, 1, 0}; // 上下左右四个方向static int[] dy = {0, 1, 0, -1};static Set<String> st;static class Node {String s; // 局面int t; // 到这个局面的步数public Node(String ss, int tt) {s = ss;t = tt;}}public static int bfs(String s1, String s2) {Queue<Node> q = new LinkedList<>();q.add(new Node(s1, 0));st.add(s1);while (!q.isEmpty()) {Node now = q.poll();String ss = now.s;int dist = now.t; // 从s1到ss的移动步数if (ss.equals(s2)) return dist; // 到达终点,返回步数int k = ss.indexOf('.'); // 句点的位置int x = k / 3, y = k % 3; // 句点坐标:第x行、第y列for (int i = 0; i < 4; i++) {int nx = x + dx[i], ny = y + dy[i]; // 让句点上下左右移动if (nx < 0 || ny < 0 || nx > 2 || ny > 2) continue; // 越界StringBuilder tmp = new StringBuilder(ss);tmp.setCharAt(k, tmp.charAt(nx * 3 + ny)); // 移动tmp.setCharAt(nx * 3 + ny, '.');if (!st.contains(tmp.toString())) {//判重,如果tmp处理过,就不再处理st.add(tmp.toString());q.add(new Node(tmp.toString(), dist + 1));}}}return -1; // 没有找到终态局面,返回-1}public static void main(String[] args) {st = new HashSet<>();Scanner scanner = new Scanner(System.in);String s1 = scanner.next();String s2 = scanner.next();System.out.println(bfs(s1, s2));}
}
3.3 Python判重
(1)用set判重
from collections import deque
dx = [-1, 0, 1, 0] # 上下左右四个方向
dy = [0, 1, 0, -1]
class Node:def __init__(self, s, t):self.s = s # 局面self.t = t # 到这个局面的步数
def bfs(s1, s2):q = deque()q.append(Node(s1, 0))st = set()st.add(s1)while q:now = q.popleft()ss = now.sdist = now.t # 从s1到ss的移动步数if ss == s2: return dist # 到达终点,返回步数k = ss.index('.')x = k // 3y = k % 3for i in range(4):nx = x + dx[i]ny = y + dy[i]if nx < 0 or ny < 0 or nx > 2 or ny > 2: continue # 越界tmp = list(ss)tmp[k], tmp[nx * 3 + ny] = tmp[nx * 3 + ny], tmp[k] # 移动tmp = ''.join(tmp)if tmp not in st: # 判重,如果tmp曾经处理过,就不再处理st.add(tmp)q.append(Node(tmp, dist + 1))return -1 # 没有找到终态局面,返回-1
s1 = input() # 初态局面s1
s2 = input() # 终态局面s2
print(bfs(s1, s2))
(2)用字典判重
from collections import deque
dx = [-1, 0, 1, 0] # 上下左右四个方向
dy = [0, 1, 0, -1]
def bfs(s1, s2):q = deque()q.append(s1)mp = {s1: 0} # 定义字典。mp[s1]=0表示s1到s1的步数是0 while q:ss = q.popleft()dist = mp[ss] # 从s1到ss的移动步数if ss == s2: return dist # 到达终点,返回步数k = ss.find('.')x = k // 3y = k % 3for i in range(4):nx = x + dx[i]ny = y + dy[i]if nx < 0 or ny < 0 or nx > 2 or ny > 2: continue # 越界tmp = list(ss)tmp[k], tmp[nx * 3 + ny] = tmp[nx * 3 + ny], tmp[k] # 移动tmp = ''.join(tmp)if tmp not in mp: # 判重,如果tmp曾经处理过,就不再处理mp[tmp] = dist + 1 # 把tmp放进map,并赋值。mp[tmp]等于s1到tmp的步数q.append(tmp)return -1 # 没有找到终态局面,返回-1
s1 = input() # 初态局面s1
s2 = input() # 终态局面s2
print(bfs(s1, s2))
习题:
洛谷搜索提单:https://www.luogu.com.cn/training/112#problems
相关文章:

<蓝桥杯软件赛>零基础备赛20周--第14周--BFS
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集 20周的完整安排请点击:20周计划 每周发1个博客,共20周。 在QQ群上交流答疑&am…...
openEuler安装Docker艰辛路程
文章目录 安装docker测试docker关于windows docker拉取镜像查看所有镜像删除镜像删除不在运行的进程强制删除正在运行的进程 启动docker容器服务-d测试 停止docker容器服务查看docker启动进程更新容器(没有自启动功能,更新为自启动)docker端口映射进入容器修改内容退…...

python图像处理总结
等我有时间了,好好总结一下这几个图像处理包,为后面的研究做个铺垫 skimage包 可以用系统自带的图片,不用自己找图片 from skimage.io import imread, imshow from skimage import data image data.astronaut() imshow(image)后面可以拿这…...

腐烂的橘子 -- DFS、BFS
994. 腐烂的橘子 class OrangesRotting:"""994. 腐烂的橘子https://leetcode.cn/problems/rotting-oranges/description/"""def solution(self, grid: List[List[int]]) -> int:"""BFS时间复杂度 O(M*N)空间复杂度 O(M*N):par…...
java swing UI第三方设计器JFormDesiner和FlatLaf UI
安装JFormDesiner 官网:https://www.formdev.com/ 先去IDEA的插件市场安装吧 JFormDesiner是非开源,且付费的插件,可以自己去找找不付费的使用方法。在swing可视化设计UI非常高效快捷,初学者可能需要一定时间探索,熟…...

前端JS实现全屏和退出全屏的效果
全屏效果想必我们都很清楚把,平时追剧看电视剧什么都会使用全屏方便我们看,我们键盘的第一个键esc可以退出全屏,那么我们如何用js实现全屏的办法呢? 设置全屏 Document.requestFullscreen(),该方法用于异步请求使元素…...

蓝桥杯C组-填充-贪心
点击此处查看原题 *思路:首先要求 00 11 尽可能的多,所以尽可能多的多配对,配对只在i , i 1之间发生,所以只需要关注str[i] 和 str[i 1]即可,如果str[i] str[i 1] ,那么一定配对&#x…...

mysql查询当天、近一周、近一个月及近一年的数据以及各种报表查询sql
以下是一些常见的MySQL查询语句,用于查询当天、近一周、近一个月和近一年的数据,以及一些常见的报表查询。 查询当天的数据: SELECT * FROM table_name WHERE DATE(date_column) CURDATE();查询近一周的数据: SELECT * FROM t…...
C# 使用Fleck创建WebSocket服务器
目录 写在前面 代码实现 服务端代码 客户端代码 调用示例 写在前面 Fleck 是 C# 实现的 WebSocket 服务器,通过 WebSocket API,浏览器和服务器只需要做一个握手的动作,然后浏览器和服务器之间就形成了一条快速通道;两者之间…...
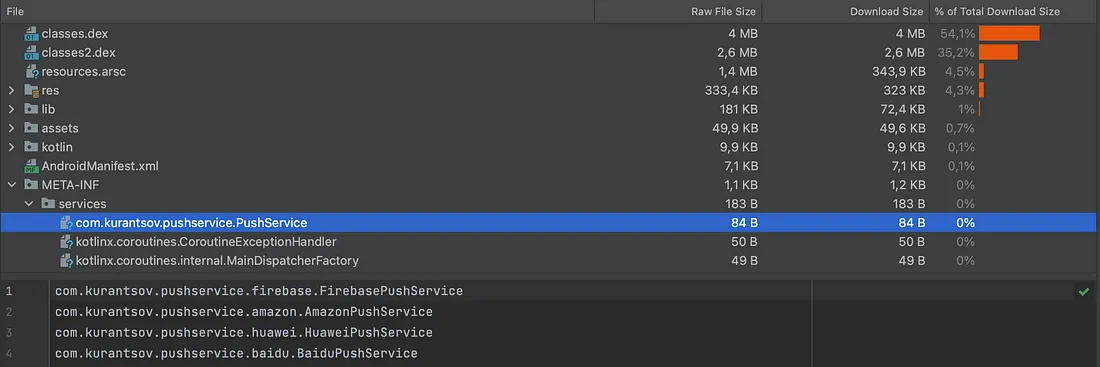
Android中的SPI实现
Android中的SPI实现 SPI是JVM世界中的标准API,但在Android应用程序中并不常用。然而,它可以非常有用地实现插件架构。让我们探讨一下如何在Android中利用SPI。 问题 在Android中,不同的提供者为推送功能提供服务,而在大型项目中…...
)
什么是设计模式(第7章笔记)
目录 一、什么是设计模式 二、设计模式概要 1、名称 2、问题 3、解决方案 4、效果 三、《设计模式》的结构 四、小结 一、什么是设计模式 设计模式:是对已经分析过的问题,以及相关问题解决方案的优秀实践; 1、同样的问题总是重复出现&…...
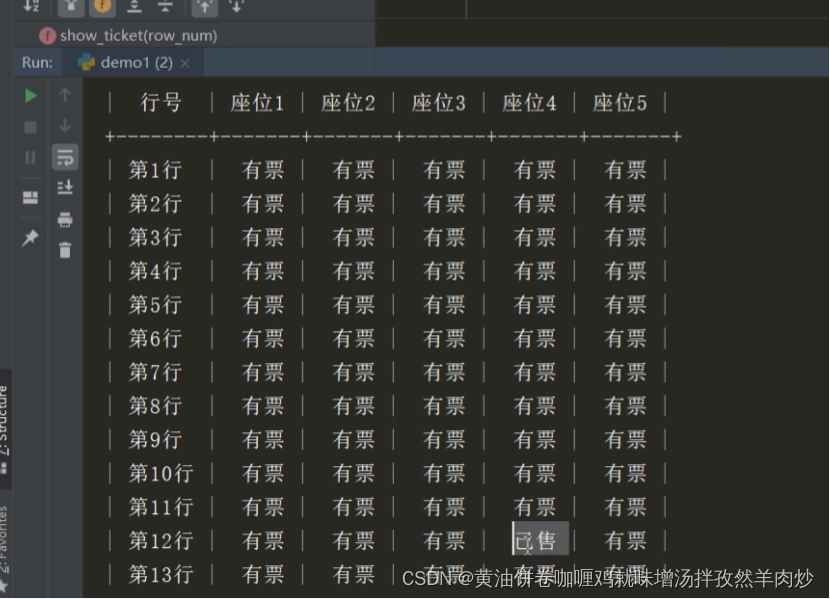
【python入门】day27: 模拟高铁售票系统
界面 代码 #-*- coding:utf-8 -*- import prettytable as pt#---------导入漂亮表格 import os.path filename ticket.txt#更新座位状态 def update(row_num):#------更新购票状态with open(filename,w,encodingutf-8) as wfile:for i in range(row_num):lst1 [f{i1},有票,有…...

智能助手的巅峰对决:ChatGPT对阵文心一言
在人工智能的世界里,ChatGPT与文心一言都是备受瞩目的明星产品。它们凭借先进的技术和强大的性能,吸引了大量用户的关注。但究竟哪一个在智能回复、语言准确性、知识库丰富度等方面更胜一筹呢?下面就让我们一探究竟。 首先来谈谈智能回复能力…...

Android系统开发之浅谈广播接收器回调
广播接器BroadcastReceiver 广播Intent和广播接收器BroadcastReceiver,是大家android开发用的特别多的二个控件。 那如何从系统角度看待广播和广播接收器呢? 对于静态注册BroadcastReceiver和动态注册的BroadcastReceiver是如何回调其onReceive方法呢…...
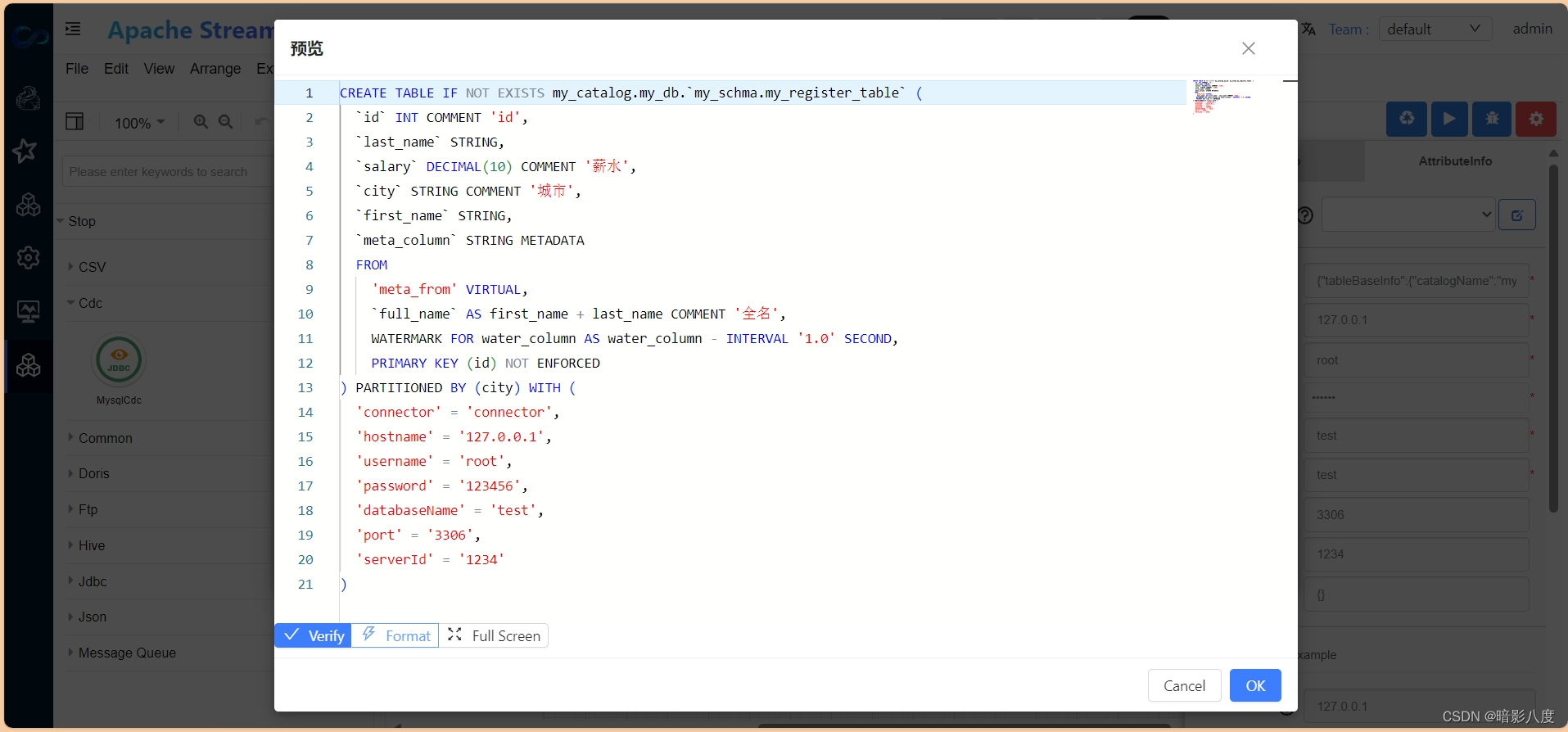
PiflowX如何快速开发flink程序
PiflowX如何快速开发flink程序 参考资料 Flink最锋利的武器:Flink SQL入门和实战 | 附完整实现代码-腾讯云开发者社区-腾讯云 (tencent.com) Flink SQL 背景 Flink SQL 是 Flink 实时计算为简化计算模型,降低用户使用实时计算门槛而设计的一套符合标…...

Mysql运算符
文章目录 比较运算符< > !IS NULL \ IS NOT NULL \ ISNULLLEAST() \ GREATEST() 查询数据大小(字典序)BETWEEN...AND...IN (SET) \ NOT IN (SET)LIKE 模糊查询REGEXP \ RLIKE 逻辑运算符逻辑运算符: OR (||)、A…...
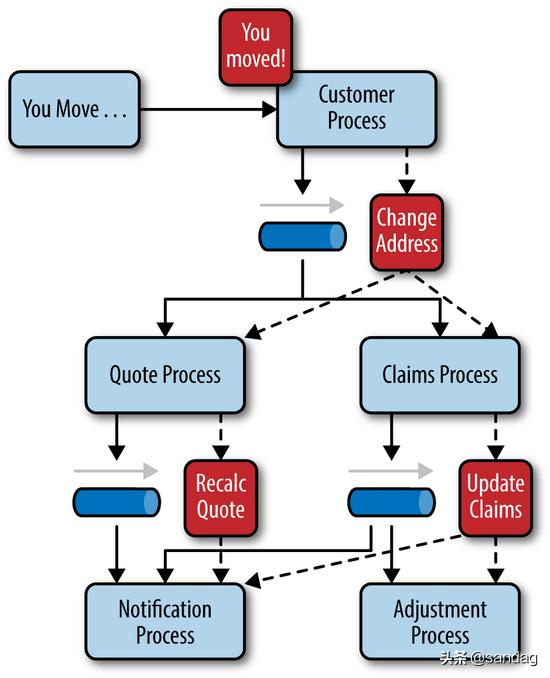
软件架构之事件驱动架构
一、定义 事件驱动的架构是围绕事件的发布、捕获、处理和存储(或持久化)而构建的集成模型。 某个应用或服务执行一项操作或经历另一个应用或服务可能想知道的更改时,就会发布一个事件(也就是对该操作或更改的记录)&am…...

C++ 后端面试 - 题目汇总
文章目录 🍺 非技术问题🍻 基本问题🥂 请自我介绍?🥂 你有什么问题需要问我的? 🍻 加班薪资🥂 你对加班有什么看法?🥂 你的薪资期望是多少?【待回…...

zds1104示波器使用指南
1、设置语言 2、功能检测验证示波器是否正常工作 3、示波器面板按钮详解 3.1、软键 3.2、运行控制与操作区 3.3、水平控制区 3.4、垂直控制区 3.5、多功能控制区 3.6、断电启动恢复,auto setup,default setup,恢复出厂设置详细解释 3.7、触…...
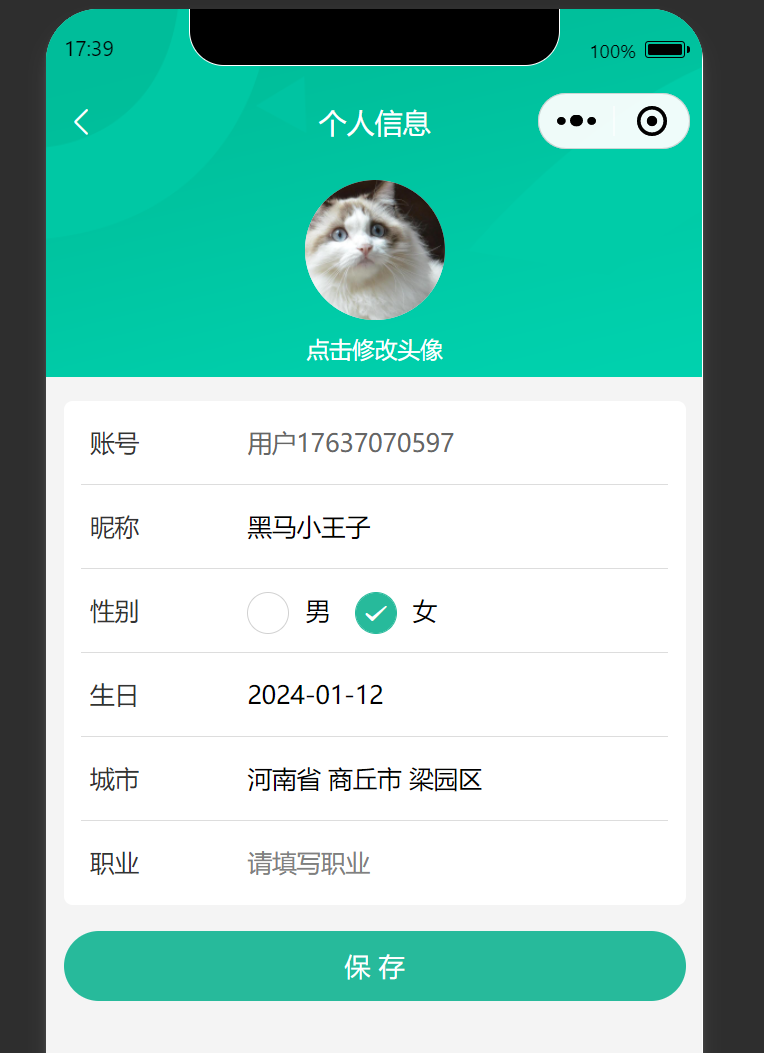
uni-app修改头像和个人信息
效果图 代码(总) <script setup lang"ts"> import { reqMember, reqMemberProfile } from /services/member/member import type { MemberResult, Gender } from /services/member/type import { onLoad } from dcloudio/uni-app impor…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
