Dijsktra算法理解笔记
Dijsktra算法理解笔记
学习了柳神的笔记 感谢柳神
Dijkstra算法是处理图问题中的最短路径的问题
最短路径问题可以大致分为两个方向
- 单源最短路径
- 全局最短路径
以此为基准可以将最短路径算法这样划分:
- 单源最短路径
- Dijkstra :不能求负权边
- Bellman-Ford:可求负
- SPFA :可求负。是2的优化
- 全局最短路径
- Floyed:可求负。
其中注意:点到点可以使用深度优先遍历
下面将着重分析Dijsktra算法
伪代码:
Dijkstra() {初始化;for(循环n次) {u = 使dis[u]最小的还未被访问的顶点的编号;记u为确定值;for(从u出发能到达的所有顶点v){if(v未被访问 && 以u为中介点使s到顶点v的最短距离更优)优化dis[v];}}
}
思想:内外循环。外循环起到遍历所有点的作用。内循环1找到还未被访问的离起点最近的点,可以理解为从起点每一步都选择最短路径,目前走到了这个点。内循环2用于找到目前走到的这个点再往下走该选择的最短路径点。
//邻接矩阵
int n, e[maxv][maxv];
int dis[maxv], pre[maxv];// pre用来标注当前结点的前一个结点
bool vis[maxv] = {false};
void Dijkstra(int s) {fill(dis, dis + maxv, inf);//初始化距离矩阵dis[s] = 0;//起点的距离置为0for(int i = 0; i < n; i++) pre[i] = i; //初始状态设每个点的前驱为自身//进入两层循环for(int i = 0; i < n; i++) {int u = -1, minn = inf;for(int j = 0; j < n; j++) {if(visit[j] == false && dis[j] < minn) {u = j;minn = dis[j];}}if(u == -1) return;visit[u] = true;for(int v = 0; v < n; v++) {if(visit[v] == false && e[u][v] != inf && dis[u] + e[u][v] < dis[v]) {dis[v] = dis[u] + e[u][v];pre[v] = u; // pre用来标注当前结点的前一个结点}}}
}
该部分为邻接矩阵情况的Dikjkstra算法实现。两个关键数组:dis[maxv]和vis[maxv]。初始起点距离置为0。在两层循环起始,设置u,标记现在访问至哪一点。若没有未访问的点,那么说明已经走完了。接着内循环2,判定u点到其余未访问点的距离,判优更新。
上述代码还加入了标注前一个结点的pre[maxv]数组。
//邻接表
struct node {int v, dis;
}
vector<vector<node>> e[maxv];
int n;
int dis[maxv], pre[maxv];// pre用来标注当前结点的前一个结点
bool visit[maxv] = {false};
for(int i = 0; i < n; i++) pre[i] = i; //初始状态设每个点的前驱为自身
void Dijkstra(int s) {fill(dis, dis + maxv, inf);dis[s] = 0;for(int i = 0; i < n; i++) {int u = -1, minn = inf;for(int j = 0; j < n; j++) {if(visit[j] == false && dis[j] < minn) {u = j;minn = dis[j];}}if(u == -1) return ;visit[u] = true;//核心区别在于这里!!for(int j = 0; j < e[u].size(); j++) {int v = e[u][j].v;if(visit[v] == false && dis[u] + e[u][j].dis < dis[v]) {dis[v] = dis[u] + e[u][j].dis;pre[v] = u;}}}
}
该部分为邻接表情况的Dijkstra算法实现。与邻接矩阵大致相同,核心区别在于内循环2的更新是如何提取边权的而已。
输出最短路径,就要用到前面设置的pre数组了。注意要倒序输出
void dfs(int s, int v) {if(v == s) {printf("%d\n", s);return ;}dfs(s, pre[v]);printf("%d\n", v);
}
至此,Dijkstra的基本操作和代码就差不多了。 下面是柳神给的三种附加考法。
- 边权+边权
以一个边权为判断最短路径的标准,另一个边权为多条最短路径时的挑选准则。
for(int v = 0; v < n; v++) { //重写v的for循环if(visit[v] == false && e[u][v] != inf) {if(dis[u] + e[u][v] < dis[v]) {dis[v] = dis[u] + e[u][v];c[v] = c[u] + cost[u][v];}else if(dis[u] + e[u][v] == dis[v] && c[u] + cost[u][v] < c[v]) {c[v] = c[u] + cost[u][v];}}
}
这里主要判断最短路径的边权为e[maxv][maxv],第二个边权为cost[maxv][maxv]。
- 边权+点权
以一个边权为判断最短路径的标准,另一个点权为多条最短路径时的挑选准则
for(int v = 0; v < n; v++) {if(visit[v] == false && e[u][v] != inf) {if(dis[u] + e[u][v] < dis[v]) {dis[v] = dis[u] + e[u][v];w[v] = w[u] + weight[v];}else if(dis[u] + e[u][v] == dis[v] && w[u] + weight[v] > w[v]) {w[v] = w[u] + weight[v];}}
}
这里主要判断最短路径的边权为e[maxv][maxv],第二个边权为weight[maxv]。
1和2的核心都在于要更新c[maxv]和w[maxv],尤其要在边权未改变时判断第二个指标(边权或者点权)。
- 问有多少条最短路径
核心在于增加一个num [ ]。起点的值置为1。其余置为0。在循环的过程中,遇到相等情况,将前一个点的路径数加到后一个点上。最后输出想要终点的值。
for(int v = 0; v < n; v++) {if(visit[v] == false && e[u][v] != inf) {if(dis[u] + e[u][v] < dis[v]) {dis[v] = dis[u] + e[u][v];num[v] = num[u];}else if(dis[u] + e[u][v] == dis[v]) {num[v] = num[v] + num[u];}}
}
柳神博文中还介绍了一个例子,非常值得学习!再次感谢柳神
相关文章:

Dijsktra算法理解笔记
Dijsktra算法理解笔记 学习了柳神的笔记 感谢柳神 Dijkstra算法是处理图问题中的最短路径的问题 最短路径问题可以大致分为两个方向 单源最短路径全局最短路径 以此为基准可以将最短路径算法这样划分: 单源最短路径 Dijkstra :不能求负权边Bellman-F…...

电流检测方法
电路检测电路常用于:高压短路保护、电机控制、DC/DC换流器、系统功耗管理、二次电池的电流管理、蓄电池管理等电流检测等场景。 对于大部分应用,都是通过感测电阻两端的压降测量电流。 一般使用电流通过时的压降为数十mV~数百mV的电阻值&…...
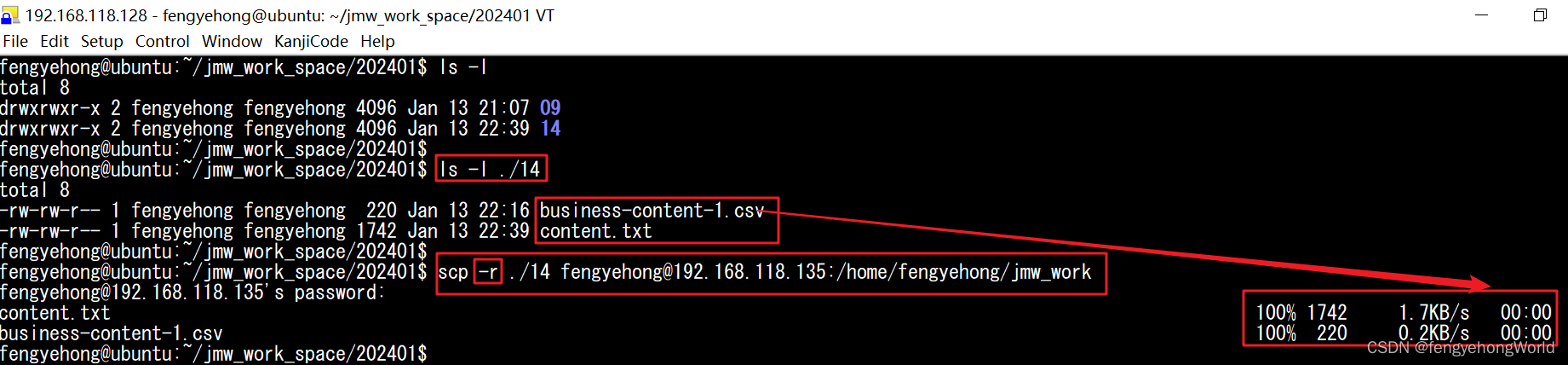
Linux scp命令 服务器之间通讯
目录 一. scp命令简介二. 本地服务器文件传输到远程服务器三. 本地服务器文件夹传输到远程服务器 一. scp命令简介 scp(Secure Copy Protocol)是用于在Unix或Linux系统之间安全地复制文件或目录的命令。 它使用SSH(Secure Shell)…...
)
C语言中的命名规则(期末版)
一、概述 命名规则是编程语言中的重要组成部分,它决定了变量、函数、常量等标符的命名方式。在C语言中,良好的命名规则可以增加代码的可读性和可维护性,提高程序的质量和开发效率。本文将详细介绍C语言中的命名规则,包括标识符的…...

远程开发之vscode端口转发
远程开发之vscode端口转发 涉及的软件forwarded port 通过端口转发,实现在本地电脑上访问远程服务器上的内网的服务。 涉及的软件 vscode、ssh forwarded port 在ports界面中的port字段,填需要转发的IP:PORT,即可转发远程服务器中的内网端…...
超简单的node爬虫小案例
同前端爬取参数一样,输入三个参数进行爬取 注意点也一样: 注意分页的字段需要在代码里面定制化修改,根据你爬取的接口,他的业务规则改代码中的字段。比如我这里总条数叫total,人家的不一定。返回的数据我这里是data.r…...
jdk api之FileFilter基础、应用、实战)
(每日持续更新)jdk api之FileFilter基础、应用、实战
博主18年的互联网软件开发经验,从一名程序员小白逐步成为了一名架构师,我想通过平台将经验分享给大家,因此博主每天会在各个大牛网站点赞量超高的博客等寻找该技术栈的资料结合自己的经验,晚上进行用心精简、整理、总结、定稿&…...
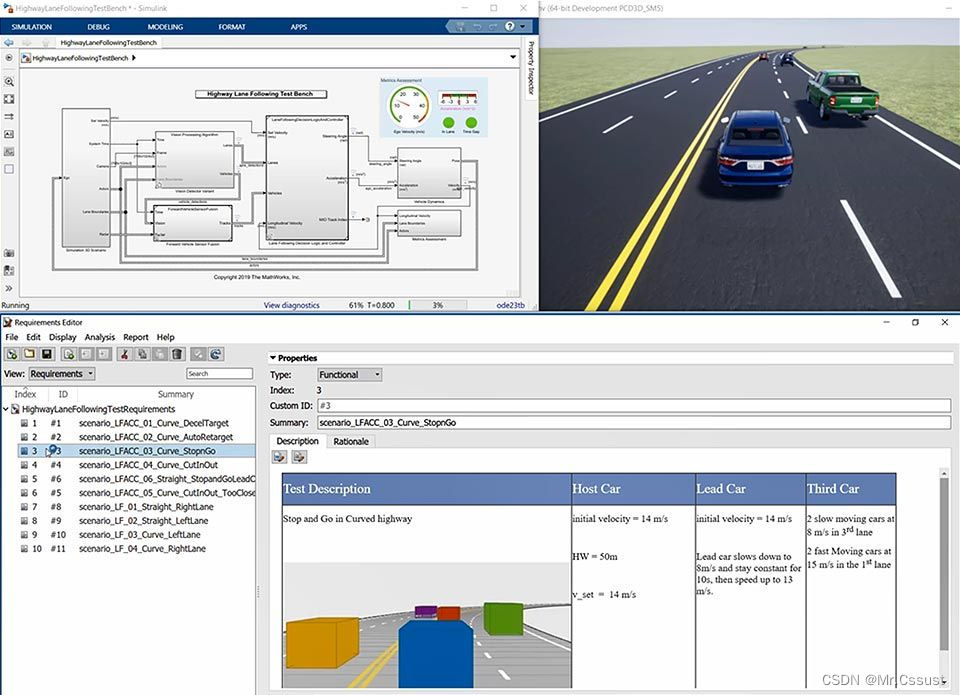
基于Matlab/Simulink开发自动驾驶的解决方案
文章目录 处理自动驾驶数据 仿真自动驾驶场景 设计感知算法 设计规划和控制算法 生成代码和部署算法 集成和测试 参考文献 使用 MATLAB/Simulink开发自动驾驶,能够深入建模真实世界的行为、减少车辆测试并验证嵌入式软件的功能,从而推进自动驾驶感…...

gitlab部署
系统版本 [rootlocalhost ~]# cat /etc/redhat-release Red Hat Enterprise Linux release 9.1 (Plow)gitlab包位置 https://mirrors.tuna.tsinghua.edu.cn/gitlab-ee/yum/el9/gitlab-ee-16.7.2-ee.0.el9.x86_64.rpm关闭防火墙 [rootlocalhost data]# systemctl stop firew…...
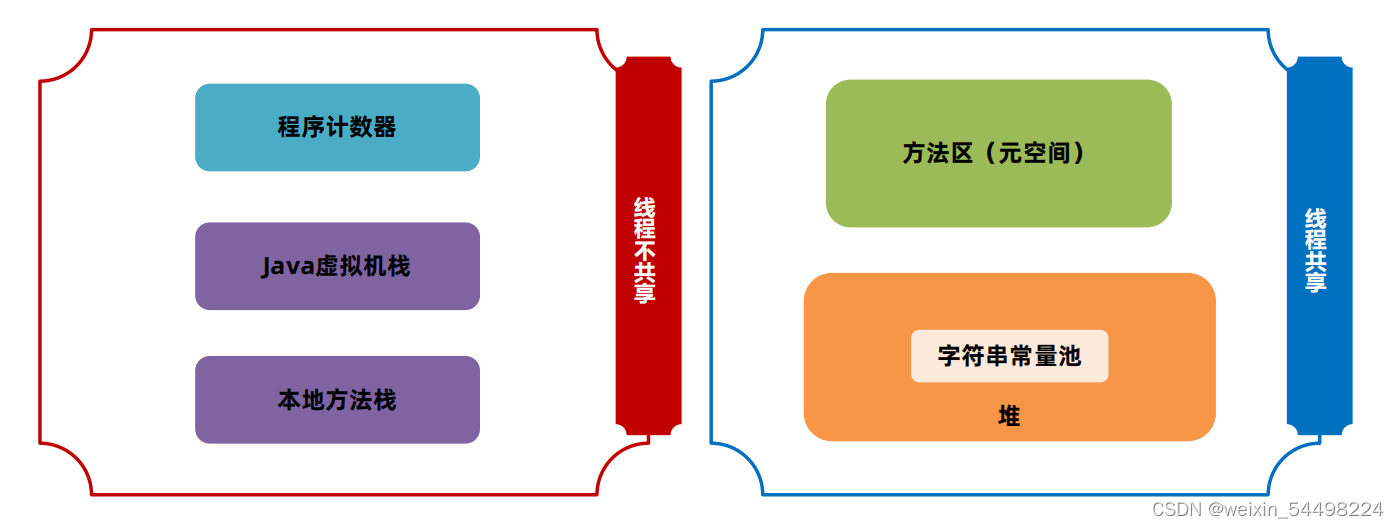
JVM运行时数据区(下篇)
紧接上篇:JVM运行时数据区(上篇)-CSDN博客 堆 一般Java程序中堆内存是空间最大的一块内存区域。创建出来的对象都存在于堆上。 栈上的局部变量表中,可以存放堆上对象的引用。静态变量也可以存放堆对象的引用,通过静态…...

生成式 AI 描绘复杂科学
生成式AI可以用来描述复杂的科学问题,主要是通过以下两种方式: 数据生成:生成式AI可以通过学习大量数据来生成新的数据,包括科学实验数据。例如,可以使用生成式AI来模拟复杂的物理实验,生成模拟数据&#…...

<蓝桥杯软件赛>零基础备赛20周--第14周--BFS
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集 20周的完整安排请点击:20周计划 每周发1个博客,共20周。 在QQ群上交流答疑&am…...
openEuler安装Docker艰辛路程
文章目录 安装docker测试docker关于windows docker拉取镜像查看所有镜像删除镜像删除不在运行的进程强制删除正在运行的进程 启动docker容器服务-d测试 停止docker容器服务查看docker启动进程更新容器(没有自启动功能,更新为自启动)docker端口映射进入容器修改内容退…...

python图像处理总结
等我有时间了,好好总结一下这几个图像处理包,为后面的研究做个铺垫 skimage包 可以用系统自带的图片,不用自己找图片 from skimage.io import imread, imshow from skimage import data image data.astronaut() imshow(image)后面可以拿这…...

腐烂的橘子 -- DFS、BFS
994. 腐烂的橘子 class OrangesRotting:"""994. 腐烂的橘子https://leetcode.cn/problems/rotting-oranges/description/"""def solution(self, grid: List[List[int]]) -> int:"""BFS时间复杂度 O(M*N)空间复杂度 O(M*N):par…...
java swing UI第三方设计器JFormDesiner和FlatLaf UI
安装JFormDesiner 官网:https://www.formdev.com/ 先去IDEA的插件市场安装吧 JFormDesiner是非开源,且付费的插件,可以自己去找找不付费的使用方法。在swing可视化设计UI非常高效快捷,初学者可能需要一定时间探索,熟…...

前端JS实现全屏和退出全屏的效果
全屏效果想必我们都很清楚把,平时追剧看电视剧什么都会使用全屏方便我们看,我们键盘的第一个键esc可以退出全屏,那么我们如何用js实现全屏的办法呢? 设置全屏 Document.requestFullscreen(),该方法用于异步请求使元素…...

蓝桥杯C组-填充-贪心
点击此处查看原题 *思路:首先要求 00 11 尽可能的多,所以尽可能多的多配对,配对只在i , i 1之间发生,所以只需要关注str[i] 和 str[i 1]即可,如果str[i] str[i 1] ,那么一定配对&#x…...

mysql查询当天、近一周、近一个月及近一年的数据以及各种报表查询sql
以下是一些常见的MySQL查询语句,用于查询当天、近一周、近一个月和近一年的数据,以及一些常见的报表查询。 查询当天的数据: SELECT * FROM table_name WHERE DATE(date_column) CURDATE();查询近一周的数据: SELECT * FROM t…...
C# 使用Fleck创建WebSocket服务器
目录 写在前面 代码实现 服务端代码 客户端代码 调用示例 写在前面 Fleck 是 C# 实现的 WebSocket 服务器,通过 WebSocket API,浏览器和服务器只需要做一个握手的动作,然后浏览器和服务器之间就形成了一条快速通道;两者之间…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
