视频SDK的技术架构优势和价值
为了满足企业对于高质量视频的需求,美摄科技推出了一款强大的视频SDK(软件开发工具包),旨在帮助企业轻松实现高效、稳定的视频功能,提升用户体验,增强企业竞争力。
一、美摄视频SDK的技术实现方式
美摄视频SDK采用了先进的技术架构,具备以下特点:
跨平台支持:美摄视频SDK支持多种主流平台,如Android、iOS、Windows、Linux等,帮助企业快速实现跨平台的音视频功能。
高性能:美摄视频SDK采用了高效的编解码算法,实现了低延迟、高清晰度的视频传输,为用户提供流畅的观看体验。
强大的实时互动功能:美摄视频SDK提供了丰富的实时互动功能,如多人语音、视频通话、屏幕共享等,满足企业多样化的沟通需求。
易于集成:美摄视频SDK提供了完善的开发文档和示例代码,企业可以轻松将其集成到自己的应用中,节省开发时间和成本。
安全可靠:美摄视频SDK采用了多重加密技术,确保音视频数据的安全可靠传输,保护企业的商业机密和个人隐私。
二、美摄视频SDK为企业带来的价值
提升用户体验:通过美摄视频SDK,企业可以实现高质量的音视频功能,为用户提供流畅、清晰的观看体验,从而提升用户满意度和忠诚度。
降低开发成本:美摄视频SDK提供了丰富的功能和易于集成的优势,企业无需投入大量人力物力进行自主研发,可以快速实现音视频功能,降低开发成本。
提高企业竞争力:通过美摄视频SDK,企业可以轻松实现高效的音视频功能,提升产品的竞争力,赢得市场份额。
拓展业务领域:美摄视频SDK提供了实时互动功能,企业可以利用这些功能拓展业务领域,如在线教育、远程医疗、在线会议等,实现业务的多元化发展。
美摄科技视频SDK凭借其先进的技术实现方式和为企业带来的价值,已经成为了众多企业的首选。如果您的企业正面临音视频功能的升级需求,不妨选择美摄视频SDK,让您的产品在激烈的市场竞争中脱颖而出。
相关文章:

视频SDK的技术架构优势和价值
为了满足企业对于高质量视频的需求,美摄科技推出了一款强大的视频SDK(软件开发工具包),旨在帮助企业轻松实现高效、稳定的视频功能,提升用户体验,增强企业竞争力。 一、美摄视频SDK的技术实现方式 美摄视…...

Invalid bound statement (not found)(xml文件创建问题)
目录 解决方法: 这边大致讲一下我的经历,不想看的直接点目录去解决方法 今天照着老师视频学习,中间老师在使用动态SQL时,直接复制了一份,我想这么简单的一个,我直接从网上找内容创建一个好了,…...

正则表达式2 常见模式
继上次的正则表达式速攻1/2-CSDN博客 还有一些常见的匹配模式可以直接使用 电子邮箱 xxxxxx.域名 的情况 \b[A-Za-z0-9._%-][A-Za-z0-9.-]\.[A-Z|a-z]{2,}\bhttp或者https网址 的情况 http[s]?://(?:[a-zA-Z]|[0-9]|[$-_.&]|[!*\\(\\),]|(?:%[0-9a-fA-F][0-9a-fA-F…...

前端对接电子秤、扫码枪设备serialPort 串口使用教程
因为最近工作项目中用到了电子秤,需要对接电子秤设备。以前也没有对接过这种设备,当时也是一脸懵逼,脑袋空空。后来就去网上搜了一下前端怎么对接,然后就发现了SerialPort串口。 Serialport 官网地址:https://serialpo…...
整数转罗马数字)
LeeCode前端算法基础100题(18)整数转罗马数字
一、问题详情: 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000 例如, 罗马数字 2 写做 II ,即为两个并列的 1…...
【C++ 程序设计入门基础】- 第4节-函数
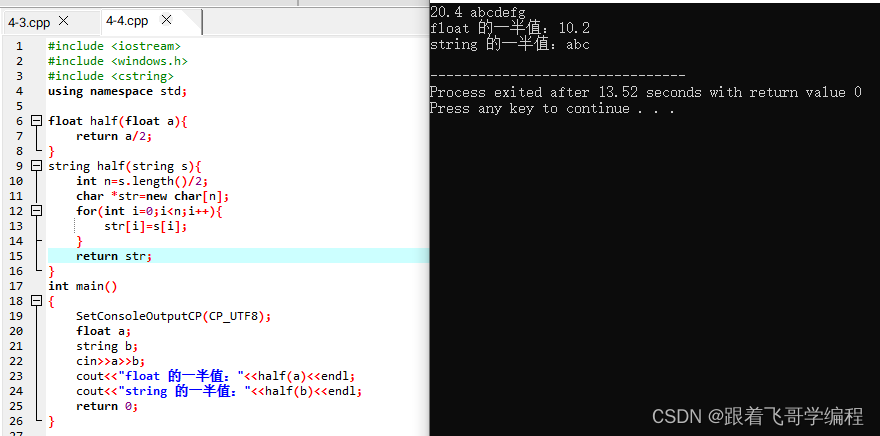
1、函数 函数是对实现某一功能的代码的模块化封装。 函数的定义: 标准函数: 输入 n 对整数的 a、b ,输出它们的和。 #include <iostream> #include <windows.h> using namespace std;int add(int a,int b);//函数原型声明int…...

华为数通HCIA题库(750题)
完整题库在这里:华为数通HCIA-RS题库注释版-加水印.pdf资源-CSDN文库 此处只节选几题。 1.网络管理员在网络中捕获到了一个数据帧,其目的MAC地址是01-00-5E-AO-B1-C3。关于该MAC地址的说法正确的是( )。 A.它是一个单播MAC地址 B.它是一个广播…...

SpringIOC之support模块GenericXmlApplicationContext
博主介绍:✌全网粉丝5W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验…...
CCF认证+蓝桥杯习题训练
贪心 *上取整公式* *代码展示* #include <iostream> #include <cstring> #include <algorithm>using namespace std;const int N 1e5 10;typedef long long LL;int v[N] , a[N];int main() {int n , d;cin >> n >> d;for(int i 1 ; i < n…...
vue前端开发自学基础,动态切换组件的显示
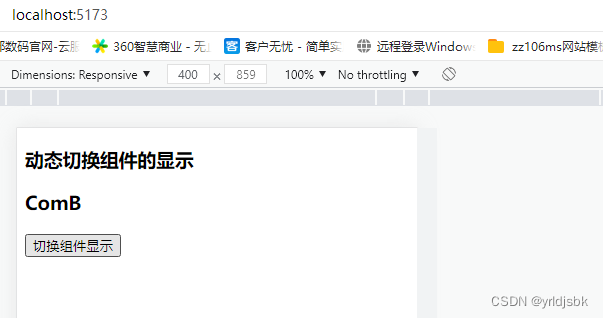
vue前端开发自学基础,动态切换组件的显示!这个是需要借助于,一个官方提供的标签,名字叫【Component】-[代码demo:<component :is"ComponetShow"></component>]。 下面看看代码详情。 <template><h3>动态…...

16.桥接模式
桥接模式 介绍 桥接模式是一种结构型设计模式,它通过将抽象部分与实现部分分离,使它们可以独立变化。这种模式通过组合的方式来实现,而不是继承。桥接模式通过将抽象和实现解耦,从而实现抽象和实现的分离,使得系统更加…...
【网络安全】【密码学】【北京航空航天大学】实验一、数论基础(上)【C语言和Java实现】
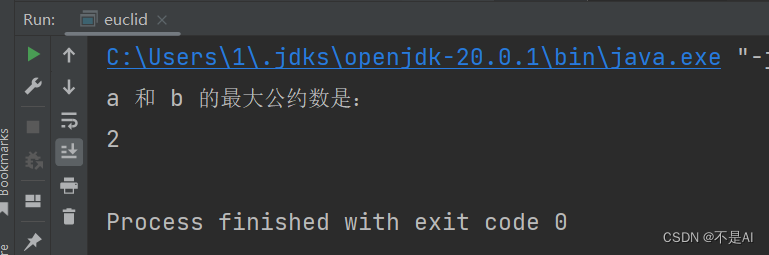
实验一、数论基础(上) 一、实验目的 1、通过本次实验,熟悉相关的编程环境,为后续的实验做好铺垫; 2、回顾数论学科中的重要基本算法,并加深对其的理解,为本学期密码学理论及实验课程打下良好…...

Go语言的sync.Pool如何使用?使用场景具体有哪些?
sync.Pool 是 Go 标准库中提供的一个对象池(Object Pool)的实现。对象池是一种用于缓存和复用对象的机制,可以在一定程度上减轻内存分配的开销。sync.Pool 专门用于管理临时对象,适用于一些需要频繁创建和销毁的短暂对象ÿ…...

MySQL单表查询练习题
一、创建表的素材 表名:worker——表中字段均为中文,比如:部门号、工资、职工号、参加工作等 CREATE TABLE worker ( 部门号 int(11) NOT NULL, 职工号 int(11) NOT NULL, 工作时间 date NOT NULL, 工资 float(8,2) NOT NULL, 政治面貌 …...

Spring MVC中@Controller和@RestController的区别
Controller 和 RestController 是 Spring MVC 中用于处理 HTTP 请求的注解,它们有以下区别: 返回值处理方式: Controller 用于定义一个传统的 Spring MVC 控制器,它的方法通常返回视图名称或 ModelAndView 对象,由视图…...
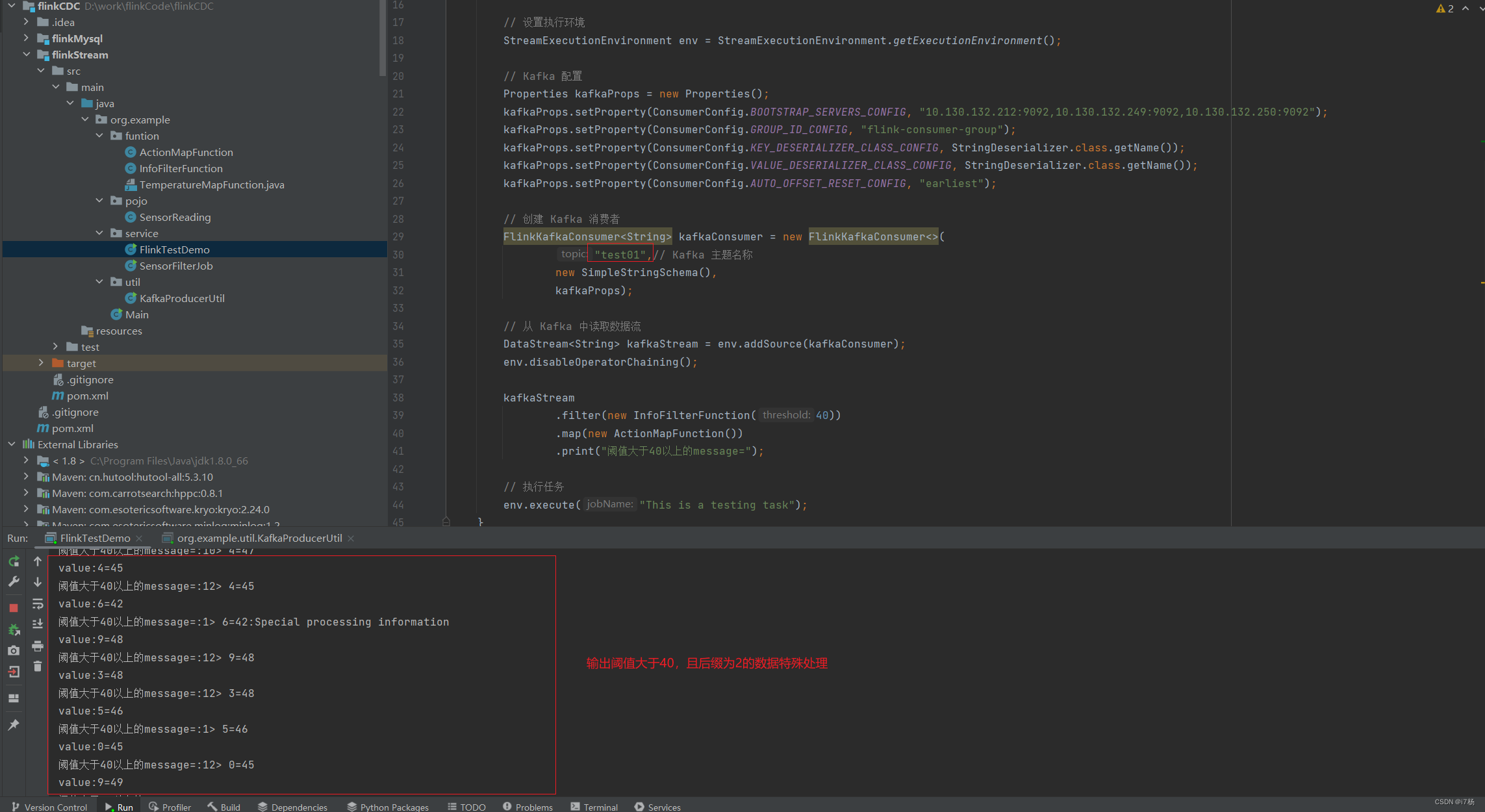
Flink定制化功能开发,demo代码
前言: 这是一个Flink自定义开发的基础教学。本文将通过flink的DataStream模块API,以kafka为数据源,构建一个基础测试环境;包含一个kafka生产者线程工具,一个自定义FilterFunction算子,一个自定义MapFunctio…...

Edge浏览器入门
关于作者: CSDN内容合伙人、技术专家, 从零开始做日活千万级APP,带领团队单日营收超千万。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、商业化变现、人工智能等,希望大家多多支持。 目录 一、导读二、概览…...

Go语言的调度器
简介 Go语言的调度器是一个非常强大的工具,它可以帮助我们轻松地实现并发编程。调度器的工作原理是将多个协程映射到多个操作系统线程上,并根据协程的状态来决定哪个协程应该在哪个线程上运行。 调度器有两种主要策略: 协作式调度…...
Linux系统使用超详细(十)~vi/vim命令①
vi/vim命令有很多,其实只有少数的用法对于我们日常工作中起到了很大帮助,但是既然我选择梳理Linux的学习笔记,那么一定全力把自己的理解和学习笔记的内容认真整理汇总,内容或许有错误,还请发现的C友们发现了及时指出。…...

C语言实现双向链表
1.版本一 由于节点之间的连接变多 所以我们最好提前将前驱节点和后继节点用变量保存下来 以免等下在进行节点之间的指向时出错 #include <stdio.h> #include <stdlib.h> #include <stdbool.h> // 节点类 typedef struct Node {// 数据域int data;// 指针域…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...

今日行情明日机会——20250609
上证指数放量上涨,接近3400点,个股涨多跌少。 深证放量上涨,但有个小上影线,相对上证走势更弱。 2025年6月9日涨停股主要行业方向分析(基于最新图片数据) 1. 医药(11家涨停) 代表标…...
