山脉数组的峰顶索引
一、题目描述
852. 山脉数组的峰顶索引
符合下列属性的数组 arr 称为 山脉数组 :
arr.length >= 3- 存在
i(0 < i < arr.length - 1)使得:arr[0] < arr[1] < ... arr[i-1] < arr[i]arr[i] > arr[i+1] > ... > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ,返回满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。
你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。

二、题目解析
本题要求算法的时间复杂度是O(logN),明显提示需要用到二分算法,但这道题数组的顺序是无序的,我们怎么使用二分去解决呢?
判断使用二分的条件并不是是否有序,而是看是否有二段性!!!
本题可以将区间划分为两个位置,第一段是逐步递增,第二段是逐步递减,而我们要查找的那个值就是在就是在递增区间的最后一个位置,因此我们可以根据条件判断当前位置的值和当前位置的前一个值进行大小比较,更具结果可以判断在哪个区间,这样可以进行二分!


三、原码
class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {//有二段性,使用二分int left = 1;int right = arr.size()-2;int mid = 0;while(left < right){mid = left + (right-left + 1)/2;if(arr[mid] > arr[mid-1])left = mid;elseright = mid-1;}return right;}
};
相关文章:

山脉数组的峰顶索引
一、题目描述 852. 山脉数组的峰顶索引 符合下列属性的数组 arr 称为 山脉数组 : arr.length > 3存在 i(0 < i < arr.length - 1)使得: arr[0] < arr[1] < ... arr[i-1] < arr[i] arr[i] > arr[i1] > .…...
openssl3.2 - 官方demo学习 - cms - cms_ver.c
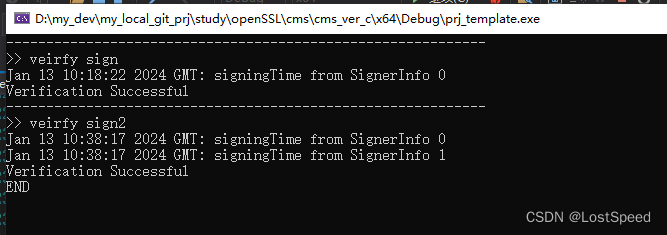
文章目录 openssl3.2 - 官方demo学习 - cms - cms_ver.c概述运行结果笔记END openssl3.2 - 官方demo学习 - cms - cms_ver.c 概述 CMS验签, 将单独签名和联合签名出来的签名文件都试试. 验签成功后, 将签名数据明文写入了文件供查看. 也就是说, 只有验签成功后, 才能看到签名…...

数据结构:堆和堆排序
数据结构:堆和堆排序 文章目录 数据结构:堆和堆排序1.二叉树的存储结构1.顺序结构2.链式结构 2.堆3.堆的实现4.堆排序(选择排序中的一类)1. 基本思想2.代码实现 1.二叉树的存储结构 1.顺序结构 顺序结构存储就是使用数组来表示一…...

力扣精选算法100题——水果成篮(滑动窗口专题)
本题链接👉水果成篮 第一步:了解题意 我就按照实例1来进行对这题的理解。 1代表种类类型,这个数组里面有2个种类类型 ps:种类1和种类2 ,只不过种类1是有2个水果,种类2有一个水果,共计3个水果。 本题需要解…...

【提示学习论文六】MaPLe: Multi-modal Prompt Learning论文原理
文章目录 MaPLe: Multi-modal Prompt Learning 多模式提示学习文章介绍动机MaPLe:Multi-modal Prompt Learning 模型结构1、Deep Language Prompting 深度语言提示2、Deep Vision Prompting 深度视觉提示3、Vision Language Prompt Coupling 视觉语言提示耦合提示耦合过程 实验…...
wpf使用Popup封装数据筛选框
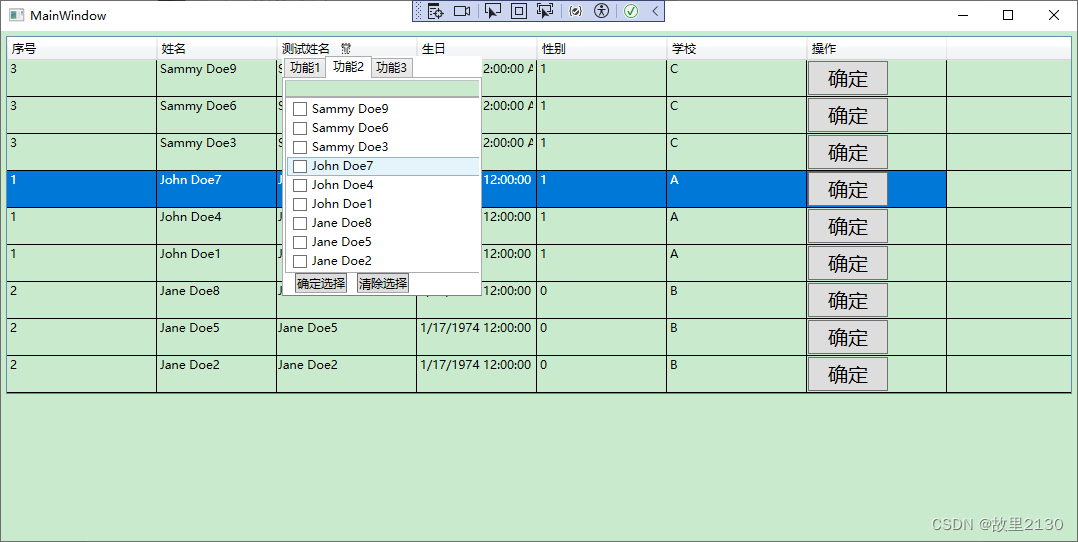
(关注博主后,在“粉丝专栏”,可免费阅读此文) 类似于DevExpress控件的功能 这是DevExpress的winform筛选样式,如下: 这是DevExpress的wpf筛选样式,如下: 这是Excel的筛选样式,如下: 先看效果 本案例使用wpf原生控件封装,功能基本上都满足,只是颜色样式没有写…...

微信小程序 - 视图与逻辑 介绍
文章目录 视图与逻辑一、页面导航1、页面导航 - 声明式导航1.1 导航到tabBar页面1.2 导航到非tabBar页面1.3 后退导航 2、页面导航 - 编程式导航2.1 导航到tabBar页面2.2 导航到非tabBar页面2.3 后退导航 3、页面导航 - 导航传参3.1 声明式导航传参3.2 编程式导航传参3.3 在 on…...
大创项目推荐 深度学习疫情社交安全距离检测算法 - python opencv cnn
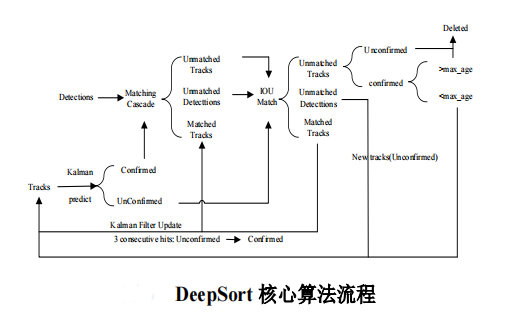
文章目录 0 前言1 课题背景2 实现效果3 相关技术3.1 YOLOV43.2 基于 DeepSort 算法的行人跟踪 4 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于深度学习疫情社交安全距离检测算法 ** 该项目较为新颖,适合作为竞赛…...

c语言-库函数strstr()、strtok()、strerror()介绍
文章目录 前言一、库函数strstr()1.1 strstr()介绍1.2 strstr()模拟实现 二、库函数strtok()2.1 strtok()介绍 三、库函数strerror()3.1 strerror()介绍 总结 前言 本篇文章介绍c语言库函数strstr()、strtok()、strerror()的使用。 一、库函数strstr() 1.1 strstr()介绍 str…...
RIP【新华三与华为区别】
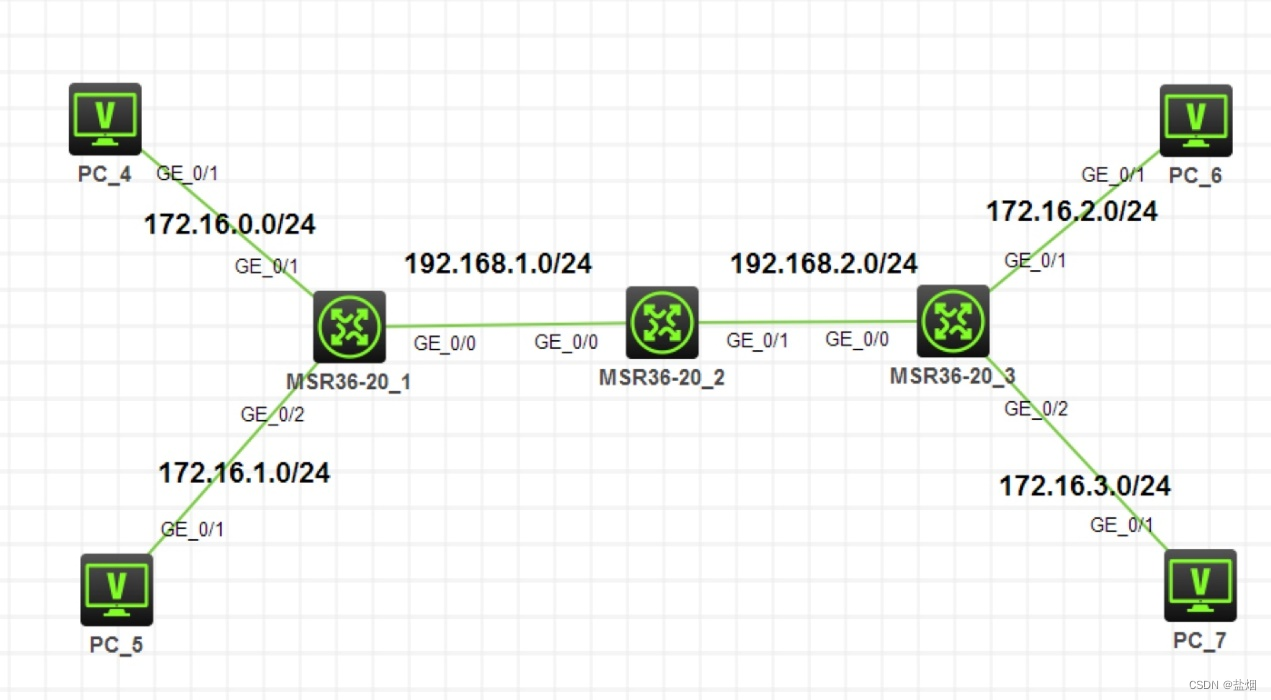
【介绍】 rip分为rip 1 与 rip 2 ,rip 2 是对 rip 1 的一种升级,rip 2 可以进行认证等功能 【命令】 新华三: [HC3-R1] rip #启用rip [HC3-R1-rip] version 2 #告知rip 版本号 [HC3-R1-rip] network 192.168.1.0 #宣告其网段 [HC3-R1-rip] …...

Python从入门到精通秘籍四
Python速成,知识点超详细,跟着这个系列边输入边学习体会吧! 一、Python的判断语句的综合案例 下面是一个使用代码示例来详细说明Python判断语句的综合案例,通过用户输入来实现简单的登录验证: # 提示用户输入用户名和密码 username = input("请输入用户名:")…...

rk3568下SoftBusDumpDeviceInfo执行错误—鸿蒙开发已解决
文章目录 项目场景:问题描述原因分析:解决方案:此Bug解决方案总结寄语项目场景: 最近也是遇到了这个问题,看到网上也有人在询问这个问题,本文总结了自己和其他人的解决经验,解决了rk3568下SoftBusDumpDeviceInfo执行错误的问题。 命令行运行 SoftBusDumpDeviceInfo,测…...

Vue 3 Composition API 详解
一、引言 在Vue 3中,引入了一个新的Composition API,旨在提供一种更灵活和可重用的方式来组织组件代码。Composition API基于函数式编程思想,允许开发者将逻辑和状态管理逻辑分离,使代码更加清晰和可维护。 二、Composition API…...
API设计:从基础到最佳实践
1*vWvkkgG6uvgmJT8GkId98A.png 在这次深入探讨中,我们将深入了解API设计,从基础知识开始,逐步进阶到定义出色API的最佳实践。 作为开发者,你可能对许多这些概念很熟悉,但我将提供详细的解释,以加深你的理解…...

每日汇评:由于中东危机削弱了风险偏好,欧元将在1.0900附近波动
随着中东危机的加深,欧元兑美元面临大幅抛售; 由于高通胀,欧洲央行决策者推迟了市场对早期降息的预期; 市场将受到周三公布的美国零售销售数据的影响; 持续的中东紧张局势增强了对避险资产的吸引力,而风险感…...

算法每日一题:删除子串后的字符串最小长度 | 栈 | 字符串
大家好,我是星恒 今天给大家带来的是一道另类的栈的应用 话不多说,我们直接来体验 题目:leetcode 2696 给你一个仅由 大写 英文字符组成的字符串 s 。你可以对此字符串执行一些操作,在每一步操作中,你可以从 s 中删除 …...
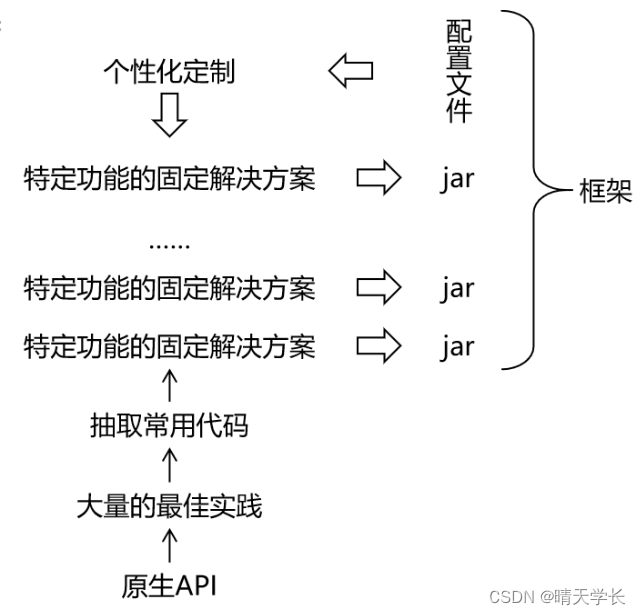
SpringFramework实战指南(一)
SpringFramework实战指南(一) 一、技术体系结构1.1 总体技术体系1.2 框架概念和理解 一、技术体系结构 1.1 总体技术体系 单一架构 一个项目,一个工程,导出为一个war包,在一个Tomcat上运行。也叫all in one。 单一架…...

AtCoder ABC198
本期F为群论题,很有难度。 C - Compass Walking 为了避免精度问题,采用二分推算。但是要小心结果为1的地方。 R 2 ∗ k 2 ≥ x 2 y 2 R^2*k^2\geq x^2y^2 R2∗k2≥x2y2 # -*- coding: utf-8 -*- # time : 2023/6/2 13:30 # file : atcoder.…...

phpinfo和php -m 加载的php.ini不一致
目的: 将phpinfo在web中展示的php.ini和在命令行中展示的php.ini加载路径设置一致。 原本的php.ini加载路劲是: /usr/local/lib/php.ini 解决思路: (1)which php 查看服务器加载的php的位置,这里原来是&a…...

121.买卖股票的最佳时机 122.买卖股票的最佳时机II
121.买卖股票的最佳时机 122.买卖股票的最佳时机II 121.买卖股票的最佳时机 力扣题目链接(opens new window) 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...
