C++力扣题目131--分割回文串
131. 分割回文串
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = "aab" 输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a" 输出:[["a"]]
提示:
1 <= s.length <= 16s仅由小写英文字母组成
思路
本题这涉及到两个关键问题:
- 切割问题,有不同的切割方式
- 判断回文
相信这里不同的切割方式可以搞懵很多同学了。
这种题目,想用for循环暴力解法,可能都不那么容易写出来,所以要换一种暴力的方式,就是回溯。
一些同学可能想不清楚 回溯究竟是如何切割字符串呢?
我们来分析一下切割,其实切割问题类似组合问题。
例如对于字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个.....。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段.....。
感受出来了不?
所以切割问题,也可以抽象为一棵树形结构,如图:

递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置,说明找到了一个切割方法。
此时可以发现,切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。
#回溯三部曲
- 递归函数参数
全局变量数组path存放切割后回文的子串,二维数组result存放结果集。 (这两个参数可以放到函数参数里)
本题递归函数参数还需要startIndex,因为切割过的地方,不能重复切割,和组合问题也是保持一致的。
在回溯算法:求组合总和(二) (opens new window)中我们深入探讨了组合问题什么时候需要startIndex,什么时候不需要startIndex。
代码如下:
vector<vector<string>> result;
vector<string> path; // 放已经回文的子串
void backtracking (const string& s, int startIndex) {
- 递归函数终止条件

从树形结构的图中可以看出:切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
那么在代码里什么是切割线呢?
在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
所以终止条件代码如下:
void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}
}
- 单层搜索的逻辑
来看看在递归循环中如何截取子串呢?
在for (int i = startIndex; i < s.size(); i++)循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。
首先判断这个子串是不是回文,如果是回文,就加入在vector<string> path中,path用来记录切割过的回文子串。
代码如下:
for (int i = startIndex; i < s.size(); i++) {if (isPalindrome(s, startIndex, i)) { // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else { // 如果不是则直接跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程,弹出本次已经添加的子串
}
注意切割过的位置,不能重复切割,所以,backtracking(s, i + 1); 传入下一层的起始位置为i + 1。
#判断回文子串
最后我们看一下回文子串要如何判断了,判断一个字符串是否是回文。
可以使用双指针法,一个指针从前向后,一个指针从后向前,如果前后指针所指向的元素是相等的,就是回文字符串了。
那么判断回文的C++代码如下:
bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;}
如果大家对双指针法有生疏了,传送门:双指针法:总结篇!(opens new window)
此时关键代码已经讲解完毕,整体代码如下(详细注释了)
根据Carl给出的回溯算法模板:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}不难写出如下代码:
class Solution {
private:vector<vector<string>> result;vector<string> path; // 放已经回文的子串void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {if (isPalindrome(s, startIndex, i)) { // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else { // 不是回文,跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程,弹出本次已经添加的子串}}bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;}
public:vector<vector<string>> partition(string s) {result.clear();path.clear();backtracking(s, 0);return result;}
};
- 时间复杂度: O(n * 2^n)
- 空间复杂度: O(n^2)
#优化
上面的代码还存在一定的优化空间, 在于如何更高效的计算一个子字符串是否是回文字串。上述代码isPalindrome函数运用双指针的方法来判定对于一个字符串s, 给定起始下标和终止下标, 截取出的子字符串是否是回文字串。但是其中有一定的重复计算存在:
例如给定字符串"abcde", 在已知"bcd"不是回文字串时, 不再需要去双指针操作"abcde"而可以直接判定它一定不是回文字串。
具体来说, 给定一个字符串s, 长度为n, 它成为回文字串的充分必要条件是s[0] == s[n-1]且s[1:n-1]是回文字串。
大家如果熟悉动态规划这种算法的话, 我们可以高效地事先一次性计算出, 针对一个字符串s, 它的任何子串是否是回文字串, 然后在我们的回溯函数中直接查询即可, 省去了双指针移动判定这一步骤.
具体参考代码如下:
class Solution {
private:vector<vector<string>> result;vector<string> path; // 放已经回文的子串vector<vector<bool>> isPalindrome; // 放事先计算好的是否回文子串的结果void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {if (isPalindrome[startIndex][i]) { // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else { // 不是回文,跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程,弹出本次已经添加的子串}}void computePalindrome(const string& s) {// isPalindrome[i][j] 代表 s[i:j](双边包括)是否是回文字串 isPalindrome.resize(s.size(), vector<bool>(s.size(), false)); // 根据字符串s, 刷新布尔矩阵的大小for (int i = s.size() - 1; i >= 0; i--) { // 需要倒序计算, 保证在i行时, i+1行已经计算好了for (int j = i; j < s.size(); j++) {if (j == i) {isPalindrome[i][j] = true;}else if (j - i == 1) {isPalindrome[i][j] = (s[i] == s[j]);}else {isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i+1][j-1]);}}}}
public:vector<vector<string>> partition(string s) {result.clear();path.clear();computePalindrome(s);backtracking(s, 0);return result;}
};
#总结
这道题目在leetcode上是中等,但可以说是hard的题目了,但是代码其实就是按照模板的样子来的。
那么难究竟难在什么地方呢?
我列出如下几个难点:
- 切割问题可以抽象为组合问题
- 如何模拟那些切割线
- 切割问题中递归如何终止
- 在递归循环中如何截取子串
- 如何判断回文
我们平时在做难题的时候,总结出来难究竟难在哪里也是一种需要锻炼的能力。
一些同学可能遇到题目比较难,但是不知道题目难在哪里,反正就是很难。其实这样还是思维不够清晰,这种总结的能力需要多接触多锻炼。
本题我相信很多同学主要卡在了第一个难点上:就是不知道如何切割,甚至知道要用回溯法,也不知道如何用。也就是没有体会到按照求组合问题的套路就可以解决切割。
如果意识到这一点,算是重大突破了。接下来就可以对着模板照葫芦画瓢。
但接下来如何模拟切割线,如何终止,如何截取子串,其实都不好想,最后判断回文算是最简单的了。
关于模拟切割线,其实就是index是上一层已经确定了的分割线,i是这一层试图寻找的新分割线
除了这些难点,本题还有细节,例如:切割过的地方不能重复切割所以递归函数需要传入i + 1。
所以本题应该是一道hard题目了。
可能刷过这道题目的录友都没感受到自己原来克服了这么多难点,就把这道题目AC了,这应该叫做无招胜有招,人码合一。
相关文章:

C++力扣题目131--分割回文串
131. 分割回文串 给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。 回文串 是正着读和反着读都一样的字符串。 示例 1: 输入:s "aab" 输出:[["a&qu…...

vue脚手架
● vue是单⻚⾯应⽤程序 ● 什么是路由 ○ 后端路由 ■ 对于普通的⽹站,所有的超链接都是URL地址,所有的URL地址都对应服务器上对应的资源 ○ 前端路由 ■ 对于单⻚⾯应⽤程序来说,主要通过URL中的hash ( # 号) 来实现不同⻚⾯之间的切换…...
Monorepo-uniapp 构建分享
Monorepo uniapp 构建灵感:刚好要做一个项目,于是想到升级一下之前自己写的一个vue3tspiniauno的模版框架,其实那个框架也不错;只是感觉还差点东西,我已经用那个小框架写了两三个项目;轻巧实用。为什么选…...
 CSRF verification failed. Request aborted.)
django后台登录:Forbidden (403) CSRF verification failed. Request aborted.
如果您在尝试登录Django后台时遇到了CSRF验证失败的错误,这通常意味着您的浏览器未能提交正确的CSRF令牌,或者Django后端未能验证该令牌。遵循以下步骤来解决这个问题: 清除浏览器Cookies和缓存: 有时候,浏览器的Cooki…...
【Python数据可视化】matplotlib之绘制常用图形:折线图、柱状图(条形图)、饼图和直方图
文章传送门 Python 数据可视化matplotlib之绘制常用图形:折线图、柱状图(条形图)、饼图和直方图matplotlib之设置坐标:添加坐标轴名字、设置坐标范围、设置主次刻度、坐标轴文字旋转并标出坐标值matplotlib之增加图形内容&#x…...

Python从入门到精通秘籍五
Python速成,每日持续更新,知识点超详细,涵盖所有Python重难点知识及其对应代码,利用碎片化时间,实现Python从入门到精通的飞跃!!! 一、Python的函数基本定义语法 当定义一个函数时,我们使用关键字def,后跟函数名称和一对圆括号。在圆括号内,可以指定任意数量的参数…...
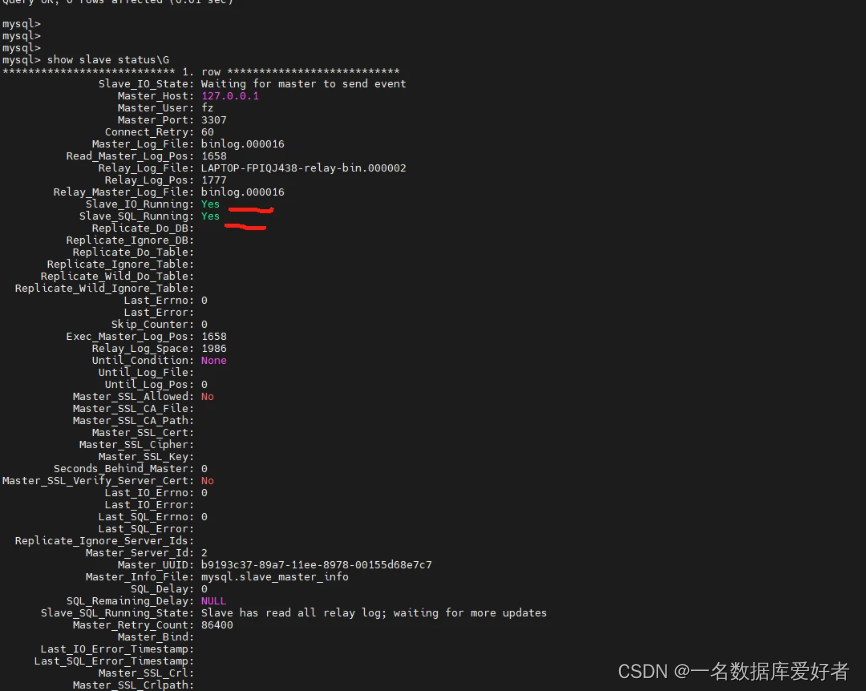
MySQL 基于 GTID 主从复制
GTID 定义 GTID 是 MySQL 事务标识,为每一个提交的事务都生成一个标识,并且是全局唯一的,这个特性是从 MySQL5.6 引进的。 组成 GTID 是由 UUID TID,UUID 是MySQL的唯一标识,每个MySQL实例之间都是不同的。TID是代表…...
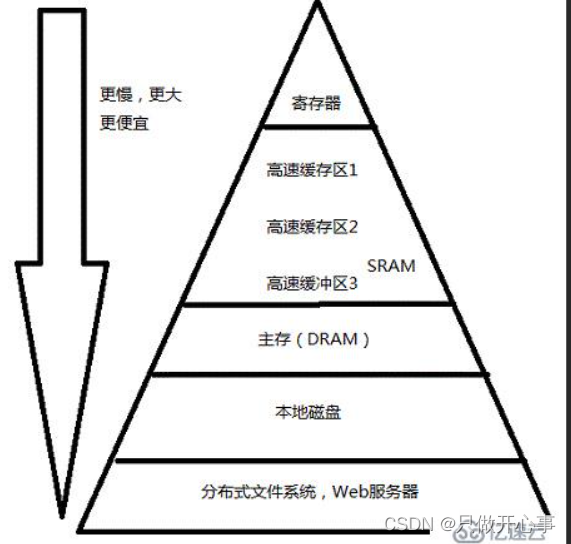
Linux操作系统基础
目录 计算机存储结构 冯.诺依曼结构 操作系统 在前几期我们学写了linux中常见的一些指令,本期我们将正式进行linux操作系统的学习。 计算机存储结构 要学习linux操作系统,我们就得先进行计算机存储结构的学习,要进行计算机存储结构的学…...

docker 批量更改镜像标签
docker 批量更改镜像标签 批量更改镜像标签批量删除镜像 批量更改镜像标签 docker images | grep "registry.aliyuncs.com\/google_containers" | sed s/registry.aliyuncs.com\/google_containers/registry.k8s.io/ | awk {print "docker tag "$3" …...

js 校验 大于等于0小于等于100
如果你想要在JavaScript中校验一个数值是否在0到100之间(包括0和100),你可以使用以下的函数: function validateRange(value) {return value > 0 && value < 100; }你可以使用这个函数来检查一个值是否在指定的范围…...

前端面试题-webpack
1.webpack是什么? 模块打包工具,用于将前端资源,如JavaScript、css、图片等打包成可以在浏览器运行的静态资源。可以将多个模块打包成一个或多个bundle。 主要功能: 模块化:可以将多个模块打包成一个或多个bundle&…...

What is `WebMvcConfigurer` does?
WebMvcConfigurer 用于自定义和扩展SpringMVC的功能配置。 比如:可以配置如视图解析器、静态资源处理、消息转换器、拦截器等MVC相关的组件。 实现 WebMvcConfigurer 接口,并使用 Configuration 注解标记,使其成为一个配置类 Configuration …...

安全强化学习笔记
这里写自定义目录标题 参考资料 Safe Reinforcement Learning环境算法CPO 2017 ICMLPCPO 2019 ICLRFOCOPS 2020 NIPSCRPO 2021 ICMLCUP 2022 NIPS TRPO 如何看懂TRPO里所有的数学推导细节? - 小小何先生的回答 - 知乎 参考资料 Safe Reinforcement Learning 安全/约束强化学…...
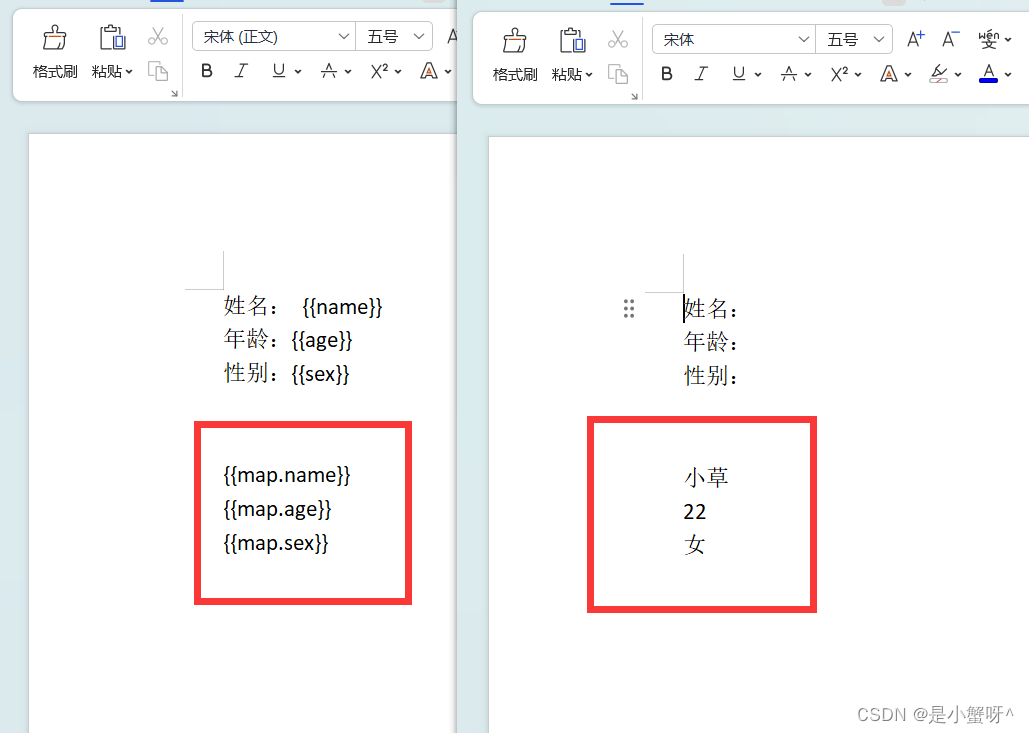
POI-tl 知识整理:整理1 -> 利用模板向word中写入数据
1 文本传值 Testpublic void testText() throws Exception {XWPFTemplate template XWPFTemplate.compile("D:\\Idea-projects\\POI_word\\templates.docx");Map<String, Object> map new HashMap<>();map.put("title", "Hi, girl"…...
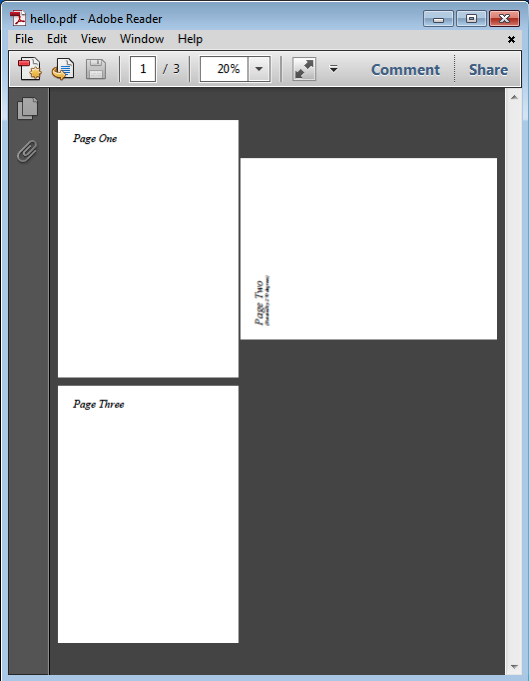
PDF结构详解
文章目录 介绍前言高保真的文件什么是PDF?PDF的一些优点版本摘要谁在使用PDF?有用的免费软件谁应该阅读 构建一个简单PDF文件基本PDF语法File StructureDocument ContentPage Content 构建简单PDF文件头目录,交叉引用表和文件尾主要对象图形内…...

Three.js 镜面反射Reflector 为MeshStandardMaterial增加Reflector能力
效果效果官方案例 区别:官方的案例更像一个镜子 没有纹理等属性 也没有透明度修改 根据源码进行修改为 MeshStandardMaterial实现反射 使用案例 createReflector() {const plane this.helper.create.plane(2, 2);this.helper.add(plane.mesh);plane.mesh.rotat…...
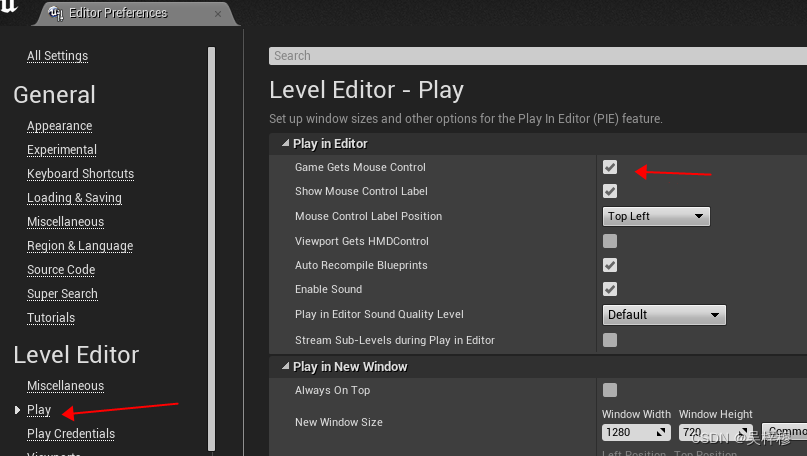
UE4使用技巧
打开蓝图编辑器时不是打开一个新窗口,而是作为主窗口 适用于全部的打开新窗口的操作 蓝图编译时自动保存 开始游戏后立即捕获鼠标...

行为型设计模式—职责链模式
职责链模式:从名字可以拆分为 职责 和 链。即能为请求创建一条由多个处理器组成的链路,每个处理器各自负责自己的职责,相互之间没有耦合,完成自己任务后请求对象即传递到链路的下一个处理器进行处理。 如果在写好的执行函数里加上…...

EndNote快速上手
前言:用EndNote主要就是为了方便管理文章引用的文献,所以本篇就是针对EndNote在文章中引用文献需要的技巧,然后本文用的是EndNoteX9。 EndNote快速上手 创建文献资料库创建文献分组导入文献手动输入文件导入在线搜索 修改文献信息去重文献删除…...
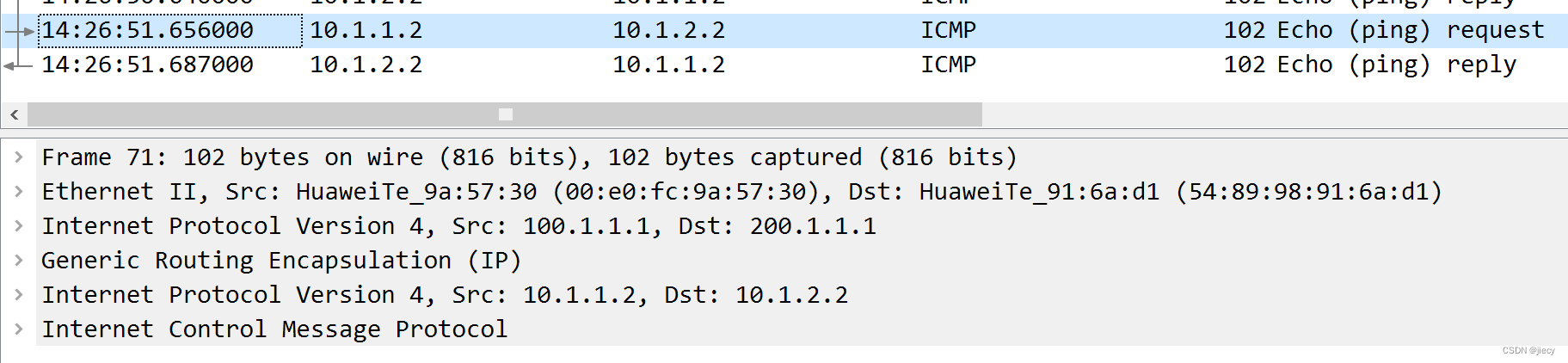
GRE隧道(初级VPN)配置步骤
一、拓朴图: 要求:1、PC1 和 PC2 能访问充当互联网接口地址的ISP环回口地址8.8.8.8 2、PC1 和 PC2 走GRE隧道互通 二、配置步骤: 1、配置IP 2、R1、R2 配置nat,代理内网地址通过G0/0/0口上外网 acl 2000rule permit source a…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
