当前位置： 首页 > news >正文

LiveGBS流媒体平台GB/T28181功能-基础配置接入控制白名单黑名单配置控制设备安全接入设备单独配置接入密码

news 2026/2/9 6:11:44

LiveGBS基础配置接入控制白名单黑名单配置控制设备安全接入设备单独配置接入密码

  • 1、白名单配置应用场景
  • 2、接入控制
    • 2.1、白名单
    • 2.2、黑名单
  • 3、搭建GB28181视频直播平台

1、白名单配置应用场景

LiveGBS国标流媒体服务，支持白名单配置。

  1. 可在设备注册前，配置白名单（设备国标编号，接入密码）；
  2. 注册接入的摄像机或是平台，优先校验白名单中配置的密码；
  3. 设备在白名单中，密码不正确时，阻止接入；
  4. 设备不在白名单中，会校验密码是否与信令服务中统一接入密码一致；

这样我们就可以为不同设备提前配置不同的接入密码，提高了接入的安全性。

2、接入控制

2.1、白名单

LiveGBS -》基础配置 -》信令服务配置 -》 接入控制 -》白名单

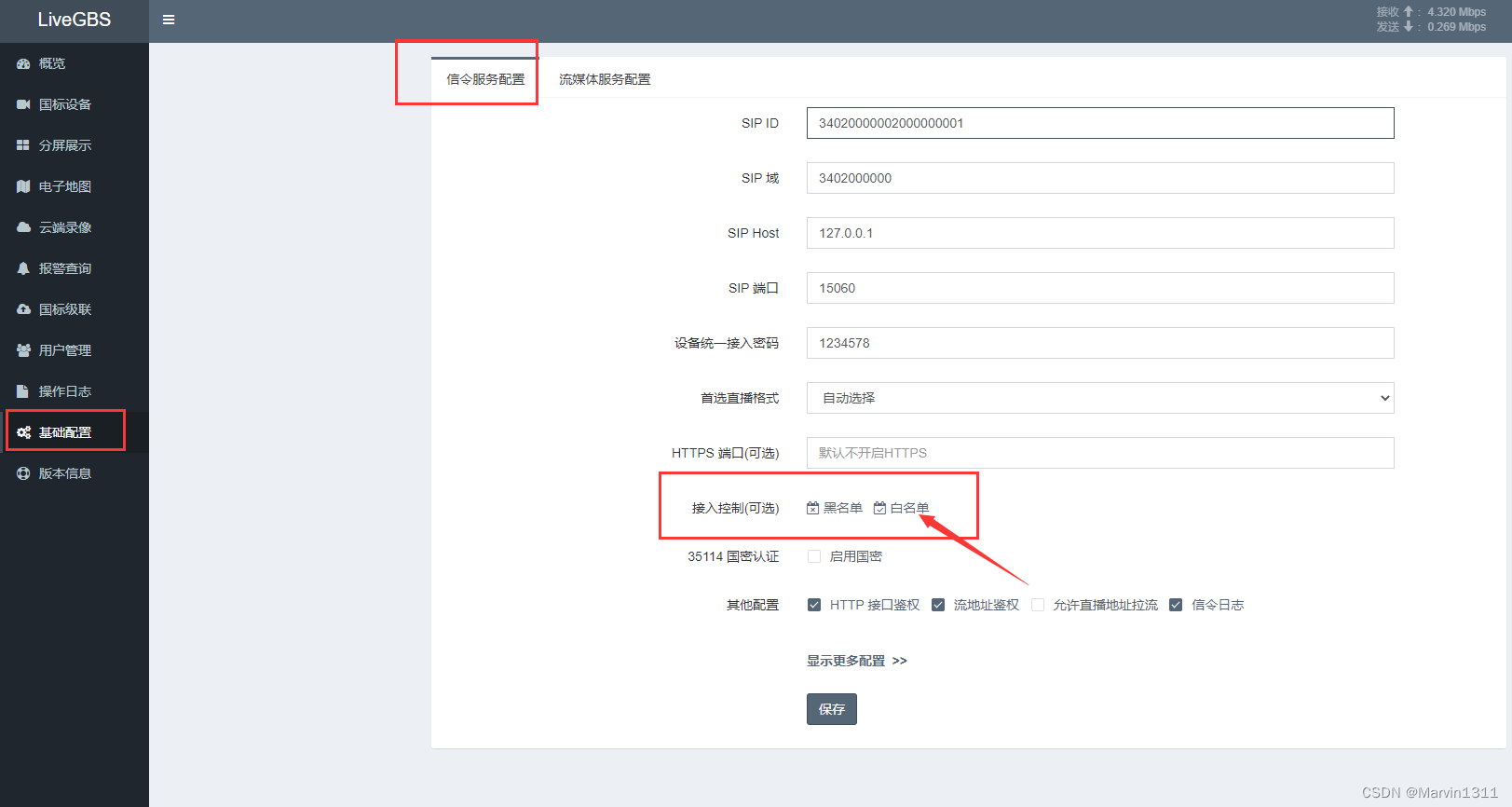
在这里插入图片描述

支持导入、导出、新增、删除

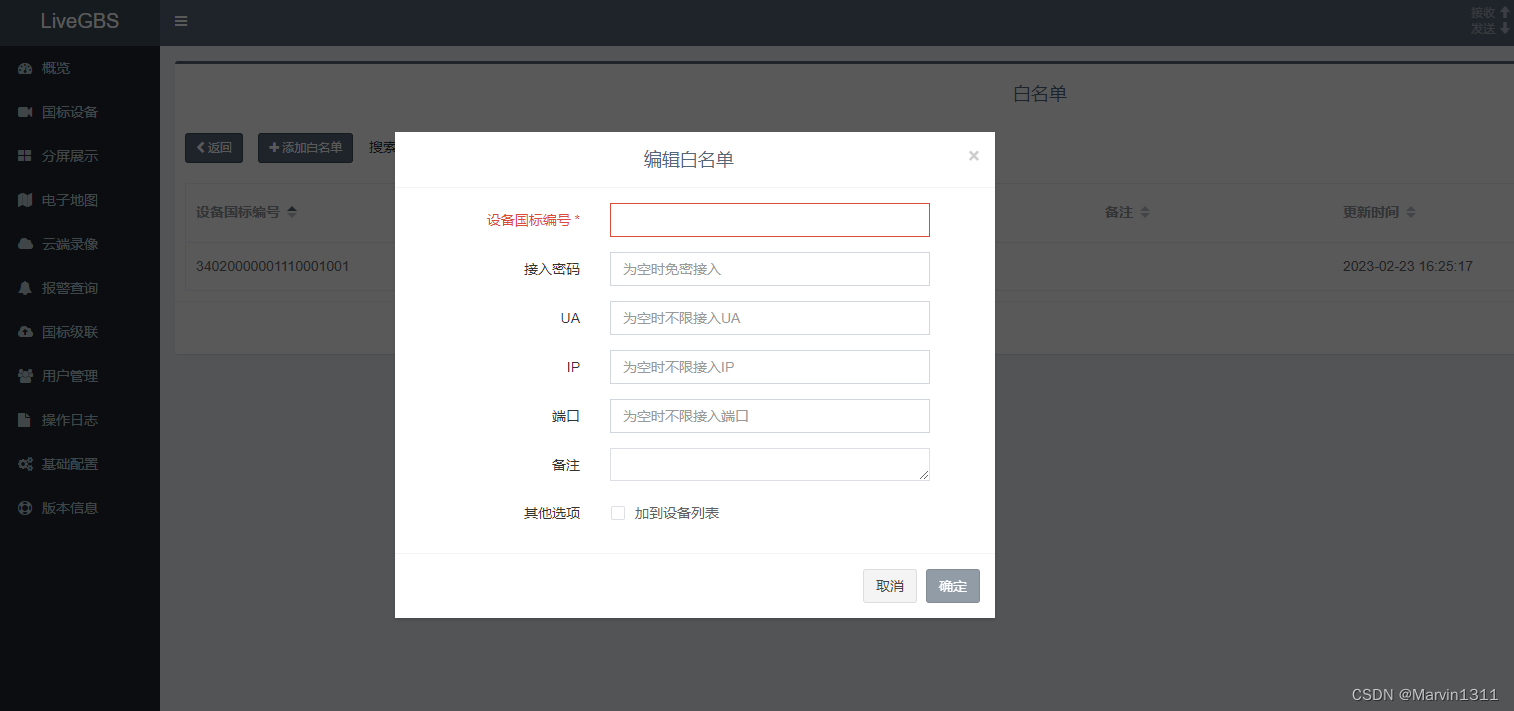
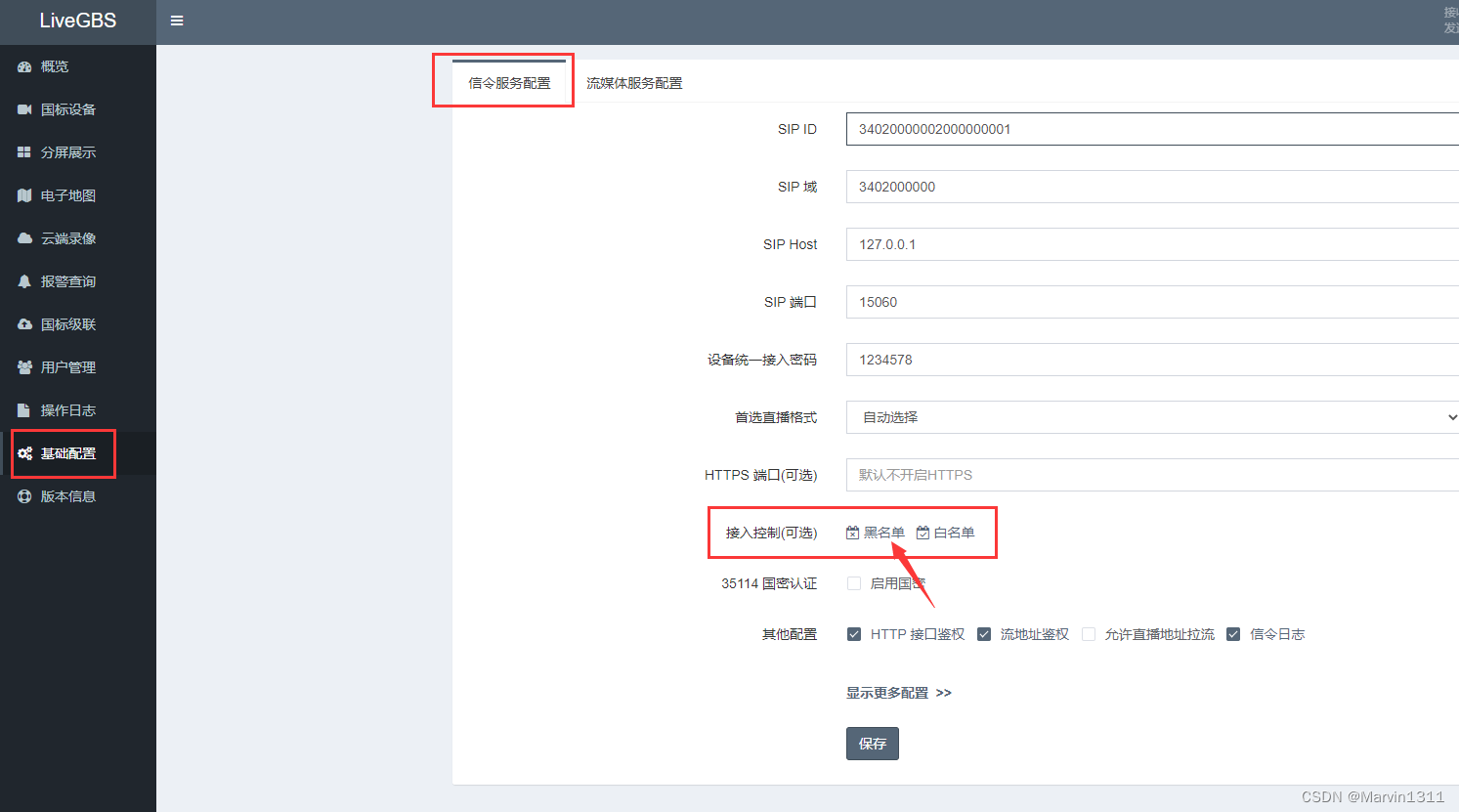
在这里插入图片描述
在这里插入图片描述

2.2、黑名单

LiveGBS -》基础配置 -》信令服务配置 -》 接入控制 -》黑名单，一些在线的设备需要删除，可以添加到黑名单，之后会强制离线，就可以删除了

在这里插入图片描述
在这里插入图片描述

3、搭建GB28181视频直播平台

  • 支持 Windows Linux 及其它CPU架构（国产、嵌入式…）操作系统
  • 安装包下载 、 安装使用说明、 WEB前端源码
  • 更多常见问题

相关文章：

LiveGBS流媒体平台GB/T28181功能-基础配置接入控制白名单黑名单配置控制设备安全接入设备单独配置接入密码

LiveGBS基础配置接入控制白名单黑名单配置控制设备安全接入设备单独配置接入密码 1、白名单配置应用场景2、接入控制2.1、白名单2.2、黑名单 3、搭建GB28181视频直播平台 1、白名单配置应用场景 LiveGBS国标流媒体服务，支持白名单配置。 可在设备注册前&#xff0…...

编程日记 2024/1/17 19:01:46

企业网站建站源码系统：Thinkphp5内核企业网站建站模板源码 带完整的安装代码包以及搭建教程

随着互联网的快速发展，企业对于网站的需求日益增强。为了满足这一市场需求，小编给大家分享一款基于Thinkphp5内核的企业网站建站源码系统。该系统旨在为企业提供一套功能强大、易于使用的网站建设解决方案，帮助企业快速搭建自己的官方网站&am…...

编程日记 2024/1/17 18:58:44

SC20-EVB ubuntu14.04 Andriod 5.1 SDK编译下载

1.ubuntu14.04安装环境配置 vi /etc/profile to add export JAVA_HOME/usr/lib/jvm/java-7-openjdk-amd64 export JRE_HOME J A V A H O M E / j r e e x p o r t C L A S S P A T H . : {JAVA_HOME}/jre export CLASSPATH.: JAVAH​OME/jreexportCLASSPATH.:{JAVA_HOME}/lib…...

编程日记 2024/1/17 18:46:32

OpenCV——图像按位运算

目录 一、算法概述1、逻辑运算2、函数解析3、用途 二、代码实现三、结果展示 OpenCV——图像按位运算由CSDN点云侠原创，爬虫自重。如果你不是在点云侠的博客中看到该文章，那么此处便是不要脸的爬虫。 一、算法概述 1、逻辑运算 OpenCV4 针对两个图像之…...

编程日记 2024/1/17 18:44:31

5 个被低估的开源项目

文章目录 1.集算器 -数据处理2. Firecamp - 邮递员替代方案3.Keploy——后端 测试4. Hanko - 密钥验证5. Zrok - Ngrok 类固醇 长话短说 本文列出了五个不太受欢迎的优秀项目，您应该尝试一下。🔥 这些工具旨在改进数据处理、API 开发、后端测试、身份验…...

编程日记 2024/1/17 18:33:21

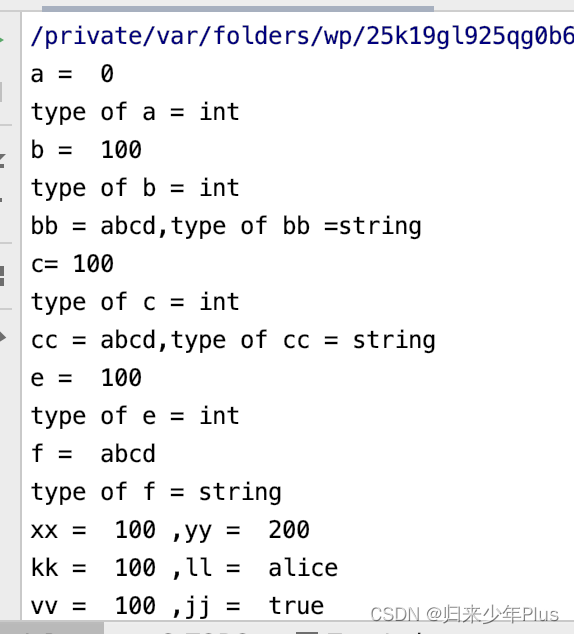
go语言初探（一）

package mainimport ("fmt""time" )func main() {fmt.Print("hello go!")time.Sleep(1 * time.Second)}运行后，结果如下： 1、golang表达式中，加；和不加；都可以 2、函数的{和函数名一…...

编程日记 2024/1/17 18:30:19

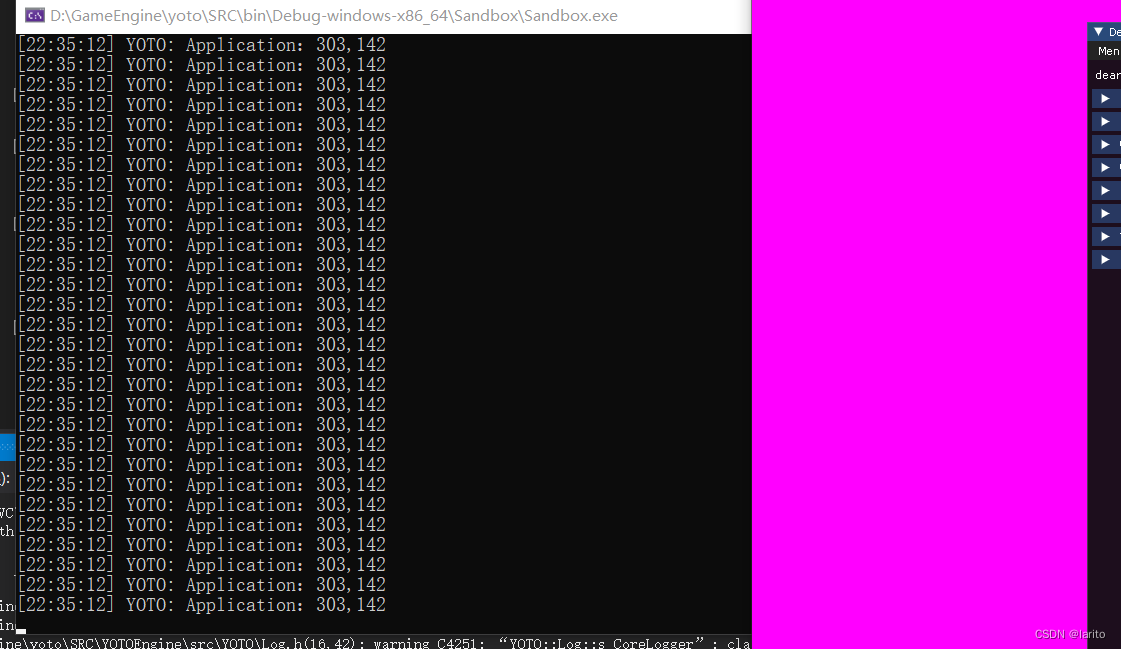
跟着cherno手搓游戏引擎【7】Input轮询

在引擎程序中任何时间，任何位置都能知道按键是否按下、鼠标的位置等等信息。 与事件系统的区别：事件系统是在按下时调用并传递按键状态；轮询是每时每刻都能获取按键状态 创建基类： YOTO/Input.h：名如其意 #pragma …...

编程日记 2024/1/17 18:28:17

stm32 - GPIO高级用法

stm32 - GPIO高级用法 PWMPWM / LEDPWM / 电机 PWM PWM / LED PWM波通过改变占空比可以改变LED的亮度 PWM信号调节LED亮度时，信号频率保持不变，即一个周期时间不变，改变的是脉冲的高电平的时间，即LED的导通时间，占空比…...

编程日记 2024/1/17 18:26:15

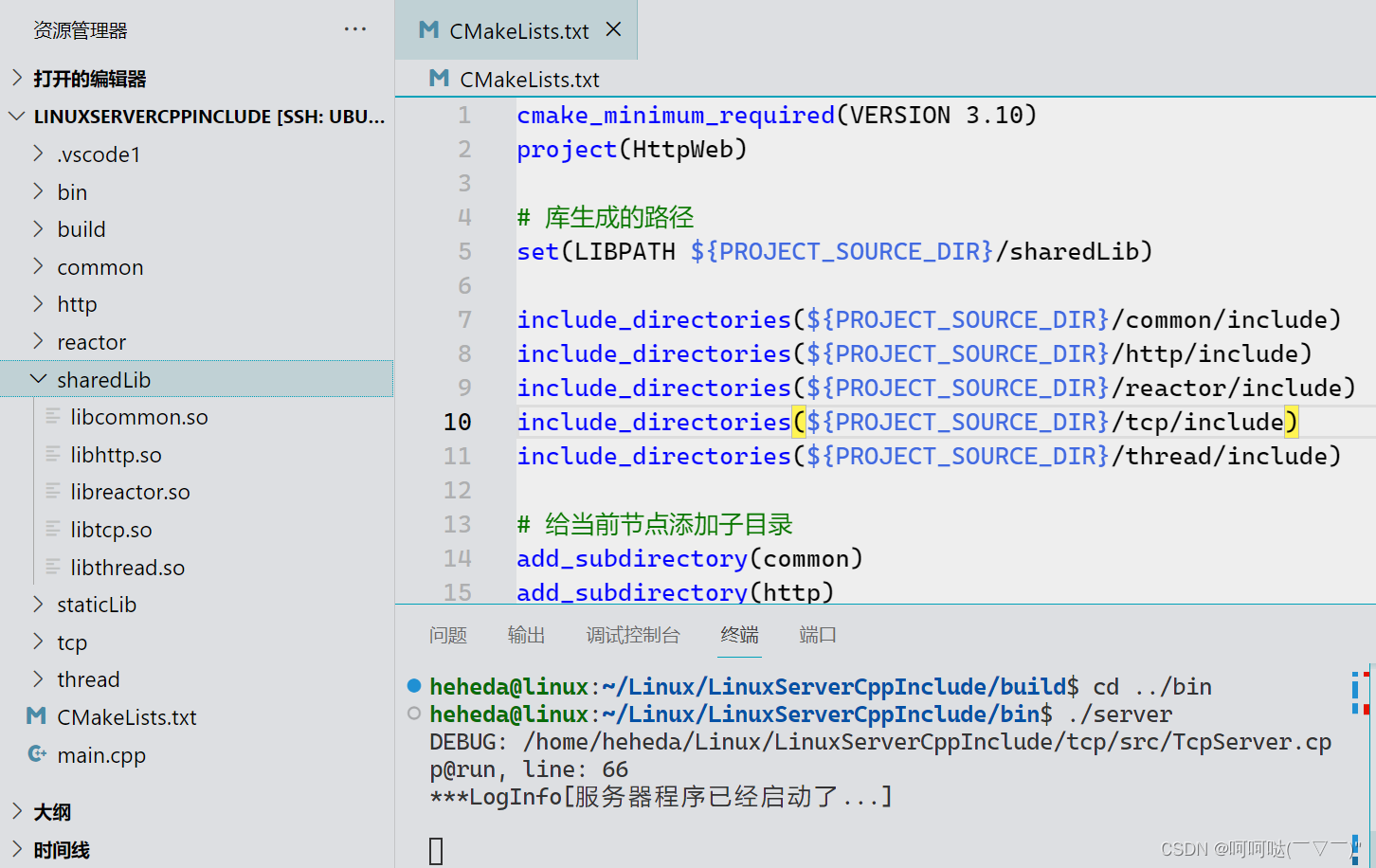
CMake TcpServer项目 生成静态库.a / 动态库.so

CMake 实战构建TcpServer项目 静态库/动态库-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/135608829?spm1001.2014.3001.5501 在这篇博客的基础上，我们把头文件放在include里边，把源文件放在src里边，重新构建 hehedali…...

编程日记 2024/1/17 18:22:12

为什么光刻要用黄光

光刻是集成电路（IC或芯片）制造中的重要工艺之一。简单来说，它是通过使用光掩膜和光刻胶在基板上复制电路图案的过程。 基板将涂覆硅二氧化层绝缘层和光刻胶。光刻胶在被紫外光照射后可以容易地用显影剂溶解，然后在腐蚀后&#xf…...

编程日记 2024/1/17 18:20:10

Python 两种多值参数

有时可能需要一个函数中处理的参数的个数是不确定的，就需要使用多值参数 参数名前加上*，代表可以接收元组参数名前加上**，代表可以接收字典 代码： def demo(*args, **kwargs):print(args)print(kwargs)demo(1, 2, 3, 4, 5, nam…...

编程日记 2024/1/17 18:19:09

【Python学习】Python学习19- 异常处理

目录 【Python学习】Python学习19- 异常处理 前言python标准异常异常处理带异常类型语法不带异常类型语法使用except而带多种异常类型try-finally 语句触发异常 参考 文章所属专区 Python学习 前言 本章节主要说明Python的异常处理。 python标准异常 BaseException 所有异常…...

编程日记 2024/1/17 18:17:07

《A++ 敏捷开发》- 4 三点估算

估算是一个范围，不是一个数 唐工：你估计完成开发用户登录模块要多少天？小李：3天。唐工：能在3天完成的可能性有多高？小李：可能性很高。唐工：可否量化一点?小李：可能性为5…...

编程日记 2024/1/17 18:16:06

cesiumlab切片通过arcgisjs加载

cesiumlab切片通过arcgisjs加载 需要注意2个地方&#xff0c;一个是tileInfo&#xff0c;一个是getTileUrl&#xff0c; 在tileInfo中定义好cesiumlab切片的相关信息。 getTileUrl 格式化url的格式。 注意设置编辑&#xff0c;避免超出范围报404。 <html lang"en"…...

编程日记 2024/1/17 18:14:04

React16源码: React中调度之scheduleWork的源码实现

scheduleWork 1 &#xff09; 概述 在 ReactDOM.render, setState, forceUpdate 这几个方法最终都调用了 scheduleWork 这个方法 在 scheduleWork 当中&#xff0c;它需要去找到更新对应的 FiberRoot 节点 在使用 ReactDOM.render 的时候&#xff0c;传给 scheduleWork 的就是…...

编程日记 2024/1/17 18:10:00

【STM32】| 02——常用外设 | I2C

系列文章目录 【STM32】| 01——常用外设 | USART 【STM32】| 02——常用外设 | I2C 失败了也挺可爱&#xff0c;成功了就超帅。 文章目录 前言1. 简介2. I2C协议2.1 I2C物理连接2.2 I2C通信协议2.2.1 起始和停止信号2.2.2 数据有效性2.2.3 数据传输格式2.2.4 从机地址/数据方…...

编程日记 2024/1/17 18:09:00

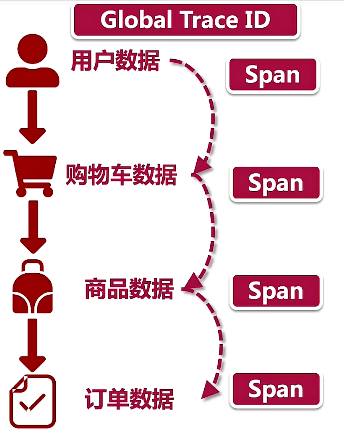
微服务架构设计核心理论：掌握微服务设计精髓

文章目录 一、微服务与服务治理1、概述2、Two Pizza原则和微服务团队3、主链路规划4、服务治理和微服务生命周期5、微服务架构的网络层搭建6、微服务架构的部署结构7、面试题 二、配置中心1、为什么要配置中心2、配置中心高可用思考 三、服务监控1、业务埋点的技术选型2、用户行…...

编程日记 2024/1/17 18:06:57

.net core 6 集成和使用 mongodb

1、安装包 MongoDB.Driver 2、定义顶层类 /// <summary> /// monggodb规范 /// </summary> public abstract class MongoDBToolBase { /// <summary> /// 客户端 /// </summary> protected MongoClient mongoClient { get; private …...

编程日记 2024/1/17 18:04:56

07-微服务getaway网关详解

一、初识网关 在微服务架构中&#xff0c;一个系统会被拆分为很多个微服务。那么作为客户端要如何去调用这么多的微服务呢&#xff1f;如果没有网关的存在&#xff0c;我们只能在客户端记录每个微服务的地址&#xff0c;然后分别去调用。这样的话会产生很多问题&#xff0c;例…...

编程日记 2024/1/17 18:03:54

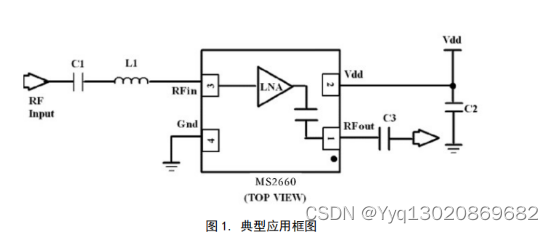
MS2660：L1 频段卫星导航射频前端低噪声放大器芯片

MS2660 是一款具有高增益、低噪声系数的低噪声放 大器&#xff08;LNA&#xff09;芯片&#xff0c;支持 L1 频段多模式全球卫星定位&#xff0c;可 以应用于 GPS、北斗二代、伽利略、Glonass 等 GNSS 导航 接收机中。芯片采用先进工艺制造&#xff0c;封装采用 2 mm 2 mm …...

编程日记 2024/1/17 18:02:53

国防科技大学计算机基础课程笔记02信息编码

1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制&#xff0c;因此这个了16进制的数据既可以翻译成为这个机器码&#xff0c;也可以翻译成为这个国标码&#xff0c;所以这个时候很容易会出现这个歧义的情况&#xff1b; 因此&#xff0c;我们的这个国…...

编程新知 2026/2/8 4:37:15

基于FPGA的PID算法学习———实现PID比例控制算法

基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容&#xff1a;参考网站&#xff1a; PID算法控制 PID即&#xff1a;Proportional&#xff08;比例&#xff09;、Integral&#xff08;积分&…...

编程新知 2026/2/8 18:25:56

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中，手势开发全攻略：

在 HarmonyOS 应用开发中&#xff0c;手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力&#xff0c;既支持点击、长按、拖拽等基础单一手势的精细控制&#xff0c;也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档&#xff0c…...

编程新知 2025/9/19 4:31:58

python/java环境配置

环境变量放一起 python&#xff1a; 1.首先下载Python Python下载地址&#xff1a;Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个&#xff0c;然后自定义&#xff0c;全选 可以把前4个选上 3.环境配置 1&#xff09;搜高级系统设置 2…...

编程新知 2026/1/24 14:23:08

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密

在实际项目中，用户注册、登录、修改密码等操作，都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输，在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

编程新知 2025/11/28 6:00:25

基于Flask实现的医疗保险欺诈识别监测模型

基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施&#xff0c;由雇主和个人按一定比例缴纳保险费&#xff0c;建立社会医疗保险基金&#xff0c;支付雇员医疗费用的一种医疗保险制度&#xff0c; 它是促进社会文明和进步的…...

编程新知 2026/1/24 14:59:08

django filter 统计数量 按属性去重

在Django中&#xff0c;如果你想要根据某个属性对查询集进行去重并统计数量&#xff0c;你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求&#xff1a; 方法1&#xff1a;使用annotate()和Count 假设你有一个模型Item&#xff0c;并且你想…...

编程新知 2026/1/11 2:37:51

MMaDA: Multimodal Large Diffusion Language Models

CODE &#xff1a; https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA&#xff0c;它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构&#xf…...

编程新知 2026/2/3 15:24:36

高等数学（下）题型笔记（八）空间解析几何与向量代数

目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

编程新知 2026/1/28 9:04:29

现代密码学 | 椭圆曲线密码学—附py代码

Elliptic Curve Cryptography 椭圆曲线密码学&#xff08;ECC&#xff09;是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础&#xff0c;例如椭圆曲线数字签…...

编程新知 2026/2/6 7:30:33