《A++ 敏捷开发》- 4 三点估算
估算是一个范围,不是一个数
唐工:你估计完成开发用户登录模块要多少天?
小李:3天。
唐工:能在3天完成的可能性有多高?
小李:可能性很高。
唐工:可否量化一点?
小李:可能性为50%~60%。
唐工:所以很有可能不止3天,要4天了。
小李:对的,其实也有可能要5、6天,但我估计概率不大。
唐工:你信心有多少?
小李:难说,有95%的信心可以在6天之内完成。
唐工:所以有可能要用上7天了?
小李:这样说吧,如果所有可能出问题的都出了问题,甚至会10天或11天,但这种概率很低。
唐工再问小李:是能否给我一个确实能完成这个模块的日期?
小李:正如我前面说,很可能3天,但也有可能4天。
唐工追问:你可以说4天吗?
小李:也有可能5、6天。
唐工结束对话:OK,请你尽力6天之内完成这个模块。
唐工貌似请求,但实际是要求小李承诺这个模块要在6天之内开发完。假如这个模块的开发时间超过6天,唐工就有依据说小李没有尽力导致延误了。
所以从以上对话,可以看到作为开发专业人员,必须分清估算和承诺。作为专业人士,我们不应该给一些没有把握的承诺,误导对方。中国老话说“一诺千金”就是这个道理。
从单点到三点估算
上面是被单点估算误导的例子,误以为那个天数是有把握达成的,所以我们最好从单点估算变成三点估算,除了估算最可能的天数,还有最佳和最差共三点。但项目是由一系列的任务组成(如第二任务依赖于第一个任务的完成),如何计算所有任务的总天数? 下面用例子说明如何用3种使用三点估算估计的方法(A、B、C)估算总天数:
A)假定都是正态分布,用模型估计:
先用PERT方程式计算每一步的预计值与标准差:
预计值 (Expected Value EV) = (Best + 4xMost Likely + Worst ) /6
标准差 (Sigma) = (Worst - Best) / 6
| 步骤Step | 最佳Best | 最可能Most Likely | 最差Worst | 预计值EV | 标准差Sigma |
| 1 | 1 | 3 | 12 | 4.167 | 1.833 |
| 2 | 1 | 1.5 | 14 | 3.5 | 2.167 |
| 3 | 3 | 6.25 | 11 | 6.5 | 1.333 |
| 10.75 | 14.168 |
如果假定是正态分布,按以上预计值和标准差,使用蒙特卡洛模拟,从下图可看到,95% 置信区间是8.02 ~ 20.37。
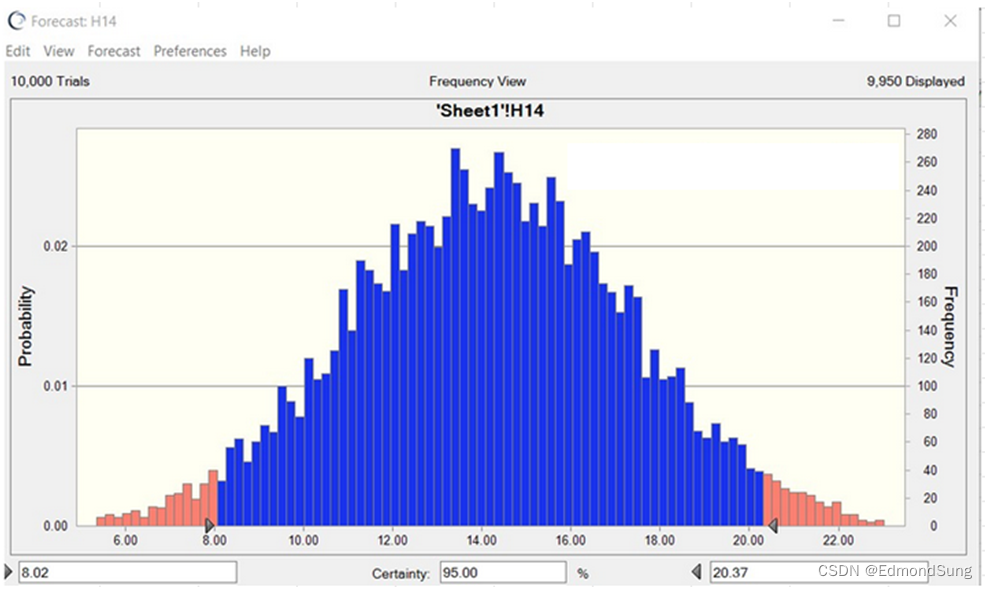
B)直接用PERT方程式计算总天数的均值与标准差:
如不用模拟,直接把3步的均值加起来:
4.2 + 3.5 + 3.6 = 14
计算3 步总方差:
(方差
假定:总方差 = 每步方差的总和
总方差= 9.77
Sigma 𝜎 = 3.13
95%范围计算公式为:均值的总和±2𝜎 = (4.2+3.5+6.5)±2𝑥3.13 = 14±6.26=7.74 ~ 20.26
结果与蒙特卡洛模拟预测类似。
C) 假定都是三角形分布,用模型估计:
如果用三角形分布,95%置信区间是 10.38 ~ 26.45。

总结 + 解读分析结果
- 如果假定每一步的分布都是一个正态分布,就可以用头两个方程式计算每一步的平均值跟标准差和方差,用方程式可计算3步的总均值大概是14。也可以用方程式计算标准差,总的标准差(sigma)是3.13左右。
- 也可用蒙特卡洛模型(假定步骤都是正态分布),得出很类似的正态分布,总的平均也接近14,95%置信区间是8.02 ~ 20.37,接近上面算出的均值 ± 两个标准差数值。
- 但因3个步骤都是明显往右偏,所以不能假设它们是正态分布,更合适的是使用三角形分布,然后用蒙特卡洛估算“加”起来的分布,看见最后的图明显是类似往右有个尾巴,能更正确反应3个步骤加起来的天数的估计分布。
- 跟假定正态分布的结果比较,很明显看到用三角形分布结果往右偏,上限是 26.45(比正态分布的20.37 高)。不是正态分布的话,左面就没有长尾巴,所以就会比本来正态分布的下限高,下限是 10.38(比正态分布的8高)。
- 从这简单例子看到,如果我们要把三点估算加起来,尤其是非正态分布的话,就不能用简单的方程式,或者假定它是正态分布来计算,需要用蒙特卡洛模型假设三角形分布才能真正反应总体的分布。
从这3个偏左分布步骤例子看起来好像有些偏差,但不是很严重。如果我们看见用10个步骤都是偏一边分布,总分布会如何?是否相差会更远?
利用蒙特卡洛模拟10个步骤(三角形分布)的总分布
如果每步都估算天数,10个步骤的总天数就是500天(把10个估算值加起来)。
但如果每个步骤都是三点估算:
| Process 过程 | 天数 | ||
| 步骤step | 最佳 | 最可能 | 最长 |
| 1 | 27 | 30 | 75 |
| 2 | 45 | 50 | 125 |
| 3 | 72 | 80 | 200 |
| 4 | 45 | 50 | 125 |
| 5 | 81 | 90 | 225 |
| 6 | 23 | 25 | 63 |
| 7 | 32 | 35 | 88 |
| 8 | 41 | 45 | 113 |
| 9 | 63 | 70 | 175 |
| 10 | 23 | 25 | 63 |
| 500 | |||
很明显看到每一步都是偏左的分布,所以可预计总天数应不止500天,但估多少才合适?
假定每步骤是三角形分布,用模型估计重复10,000次,得出下面分布:
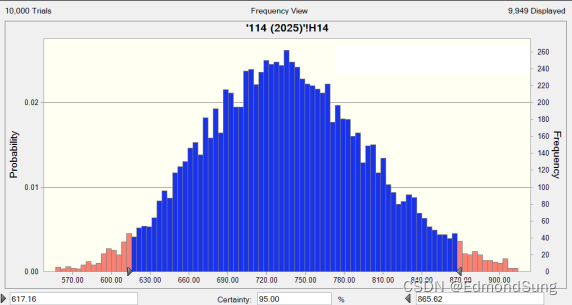
得出95%区间是 617 ~ 865
| 过程Process | 天数Durations | ||||
| 步骤step | 最佳 | 最可能 | 最差 | 预计值 | 标准差 |
| 1 | 27 | 30 | 75 | 37 | 8 |
| 2 | 45 | 50 | 125 | 61.66 | 13.33 |
| 3 | 72 | 80 | 200 | 98.66 | 21.33 |
| 4 | 45 | 50 | 125 | 61.66 | 13.33 |
| 5 | 81 | 90 | 225 | 111 | 24 |
| 6 | 23 | 25 | 63 | 31 | 6.66 |
| 7 | 32 | 35 | 88 | 43.33 | 9.33 |
| 8 | 41 | 45 | 113 | 55.66 | 12 |
| 9 | 63 | 70 | 175 | 86.33 | 18.66 |
| 10 | 23 | 25 | 63 | 31 | 6.66 |
| 500 | 617.33 | ||||
A) 用PERT方程式计算每一步的预计值与标准差:

得出95% 区间是 525.3 ~ 709.3 (= 617.3 ± 92 )
B) 假定是正态分布,按以上预计值和标准差,使用蒙特卡洛模拟,得出的总分布的结果几乎一致,都是左右平均分布的正态形。

得出95%区间是 526 ~ 707
分析10 个步骤模拟结果
- 为什么用三角形分布模拟出来不是偏左的分布(类似前面3步结果),而是一个正态分布。
以上实验验证了“中心极限定理”,无论本来是什么形状的分布,如果随机抽样够多,样本的平均值分布接近正态分布。所以如果本来只是3个步骤的时候还是可以看出是三角形偏左,但到了用10个步骤相加时,得出的分布便非常接近正态分布。
(中心极限定理会在后面数据分析里用上,例如通过画控制图判断过程是否稳定)。
- 实验结果也验证了当每一步都类似正态分布可以用PERT公式计算每一步的预计值和标准差,然后计算总结果的分布(不需要蒙特卡洛模拟),但如果非正态分布(如偏左的三角形分布)便需要使用蒙特卡洛模拟,不然预估会有偏差(类似上面3步模拟的结果)。
问答 Q&A
问:为什么要花这么多精力去研究分布,我们日常不都是单点估算吗?
答:例如你觉得把整个公司的人均生产率从1.14一年后提升到1.21算不错吗?(注)
问:不是非常好,还算可以。
答:如果本来的分布和提升后的目标是如下图,你觉得怎么样?

问:提升就太微小了。
答:从这简单例子看到所有估算都应包含两部分:分布和中间趋势(例如平均值)。
另一例子:假如我们预估生产率是的分布是如下图,达到或超越1.14 这目标的概率是65%:

但如果告诉你目标是1.14只是目标平均值,分布是如下图:

预测生产率的分布完全在目标范围之内。
( 注:生产率单位 每人天产出代码的功能点数,类似有效代码行数都是衡量软件规模的单位。)
在下一部分,我们会看到如何使用PERT三点估算的实例。
附件
蒙特卡洛(Monte Carlo)模拟
当结果不能用数学公式计算的时候(例如是三角形分布),可以用电脑随机模拟结果。例如:
- 计算3个步骤的总共人天,每个步骤的概率都是三角形分布,电脑随机功能模拟:
- 第一次模拟:步骤1得出1.3,步骤2得出1.2,步骤3得出2.0,得出3个步骤的总工期是4.5人天。
- 第二次模拟:步骤1得出1.5,步骤2得出1.15 ......。
- 如果我们模拟1000次、10000次,便能模拟出总分布。
- 因为是电脑随机模拟,出来的结果会有些偏差,但差异不会太大。(例如上面10步三角形分布的模拟结果偏差都没有低于0.3%)
相关文章:

《A++ 敏捷开发》- 4 三点估算
估算是一个范围,不是一个数 唐工:你估计完成开发用户登录模块要多少天?小李:3天。唐工:能在3天完成的可能性有多高?小李:可能性很高。唐工:可否量化一点?小李:可能性为5…...

cesiumlab切片通过arcgisjs加载
cesiumlab切片通过arcgisjs加载 需要注意2个地方,一个是tileInfo,一个是getTileUrl, 在tileInfo中定义好cesiumlab切片的相关信息。 getTileUrl 格式化url的格式。 注意设置编辑,避免超出范围报404。 <html lang"en"…...

React16源码: React中调度之scheduleWork的源码实现
scheduleWork 1 ) 概述 在 ReactDOM.render, setState, forceUpdate 这几个方法最终都调用了 scheduleWork 这个方法 在 scheduleWork 当中,它需要去找到更新对应的 FiberRoot 节点 在使用 ReactDOM.render 的时候,传给 scheduleWork 的就是…...

【STM32】| 02——常用外设 | I2C
系列文章目录 【STM32】| 01——常用外设 | USART 【STM32】| 02——常用外设 | I2C 失败了也挺可爱,成功了就超帅。 文章目录 前言1. 简介2. I2C协议2.1 I2C物理连接2.2 I2C通信协议2.2.1 起始和停止信号2.2.2 数据有效性2.2.3 数据传输格式2.2.4 从机地址/数据方…...
微服务架构设计核心理论:掌握微服务设计精髓
文章目录 一、微服务与服务治理1、概述2、Two Pizza原则和微服务团队3、主链路规划4、服务治理和微服务生命周期5、微服务架构的网络层搭建6、微服务架构的部署结构7、面试题 二、配置中心1、为什么要配置中心2、配置中心高可用思考 三、服务监控1、业务埋点的技术选型2、用户行…...

.net core 6 集成和使用 mongodb
1、安装包 MongoDB.Driver 2、定义顶层类 /// <summary> /// monggodb规范 /// </summary> public abstract class MongoDBToolBase { /// <summary> /// 客户端 /// </summary> protected MongoClient mongoClient { get; private …...
07-微服务getaway网关详解
一、初识网关 在微服务架构中,一个系统会被拆分为很多个微服务。那么作为客户端要如何去调用这么多的微服务呢?如果没有网关的存在,我们只能在客户端记录每个微服务的地址,然后分别去调用。这样的话会产生很多问题,例…...
MS2660:L1 频段卫星导航射频前端低噪声放大器芯片
MS2660 是一款具有高增益、低噪声系数的低噪声放 大器(LNA)芯片,支持 L1 频段多模式全球卫星定位,可 以应用于 GPS、北斗二代、伽利略、Glonass 等 GNSS 导航 接收机中。芯片采用先进工艺制造,封装采用 2 mm 2 mm …...

微信小程序防止截屏录屏
一、使用css添加水印 使用微信小程序原生的view和css给屏幕添加水印这样可以防止用户将小程序内的隐私数据进行截图或者录屏分享导致信息泄露,给小程序添加一个水印浮层。这样即使被截图或者拍照,也能轻松地确定泄露的源头。效果图如下: 代码…...

126.(leaflet篇)leaflet松散型arcgis缓存切片加载
地图之家总目录(订阅之前必须详细了解该博客) arcgis缓存切片数据格式如下: 完整代码工程包下载,运行如有问题,可“私信”博主。效果如下所示: leaflet松散型arcgis缓存切片加载 下面献上完整代码,代码重要位置会做相应解释 <!DOCTYP...
物联网介绍
阅读引言: 本文从多方面叙述物联网的定义以及在物联网当中的各种通信的介绍。 一、物联网的定义 1.1 通用的定义 物联网(Internet of Things,IOT;也称为Web of Things)是指通过各种信息传感设 备,如传感器、…...

Flume 之自定义Sink
1、简介 前文我们介绍了 Flume 如何自定义 Source, 并进行案例演示,本文将接着前文,自定义Sink,在这篇文章中,将使用自定义 Source 和 自定义的 Sink 实现数据传输,让大家快速掌握Flume这门技术。 2、自定…...
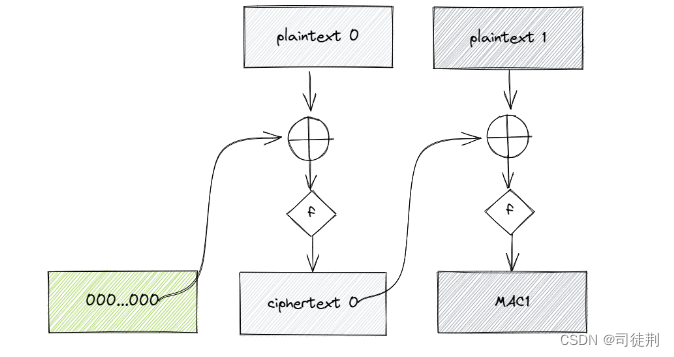
【1】SM4 CBC-MAC 机制
0x01 题目 MSG1: e55e3e24a3ae7797808fdca05a16ac15eb5fa2e6185c23a814a35ba32b4637c2 MAC1: 0712c867aa6ec7c1bb2b66312367b2c8 ----------------------------------------------------- MSG2: d8d94f33797e1f41cab9217793b2d0f02b93d46c2ead104dce4bfec453767719 MAC2: 4366…...
)
响应式编程Reactor API大全(下)
Reactor 是一个基于响应式编程的库,主要用于构建异步和事件驱动的应用程序。Reactor 提供了丰富的 API,包括创建、转换、过滤、组合等操作符,用于处理异步数据流。以下是一些 Reactor 的主要 API 示例: pom依赖 <dependencyMan…...

【STM32】HAL库的STOP低功耗模式UART串口唤醒,解决首字节出错的问题(全网第一解决方案)
【STM32】HAL库的STOP低功耗模式UART串口唤醒,解决首字节出错的问题(全网第一解决方案) 前文: 【STM32】HAL库的STOP低功耗模式UART串口唤醒,第一个接收字节出错的问题(疑难杂症) 目前已解决 …...

Python 语法糖
一、基本概念 语法糖,可以理解为:“甜蜜” 的便捷语法。 它是编程语言为程序提供的更简洁、更易读的语法实现的语法结构,它并不影响语言的功能,仅仅是一种更便捷的书写方式。 这就像你制作蛋糕时,使用现代烤箱而不是…...
一个小程序跳转到另一个小程序中如何实现
小程序 保证两个小程序是一样的主体才可以跳转。怎么知道是不是同样的主体呢? 小程序的后台管理-设置-基本设置-基本信息。查看主体信息。 跳转 <button clicktoOtherMini()>跳转到另一个小程序</button> function toOtherMini(){wx.navigateToMini…...
STM32+HAL库驱动ADXL345传感器(SPI协议)
STM32HAL库驱动ADXL345传感器(SPI协议) ADXL345传感器简介实物STM32CubeMX配置SPI配置片选引脚配置串口配置 特别注意(重点部分)核心代码效果展示 ADXL345传感器简介 ADXL345 是 ADI 公司推出的基于 iMEMS 技术的 3 轴、数字输出加…...
Redis实现全局唯一Id
一、全局唯一ID 每个店铺都可以发布优惠券: 当用户抢购时,就会生成订单并保存到tb_voucher_order这张表中,而订单表如果使用数据库自增ID就存在一些问题: id的规律性太明显 受单表数据量的限制 场景分析:如果我们的…...
【J-Flash基本使用总结】
【J-Flash基本使用总结】 VX:hao541022348 ■ 烧录文件■ 创建新的工程■ 烧录模式-SWD模式■ J-Flash下载程序到单片机 ■ J-Flash拼接多个hex或bin文件■ J-Flash读单片机的option byte■ J-Flash读单片机Flash数据■ 将读出来的文件用jflash烧录到其他的芯片■ 设…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
