Python 两种多值参数
有时可能需要一个函数中处理的参数的个数是不确定的,就需要使用多值参数
- 参数名前加上*,代表可以接收元组
- 参数名前加上**,代表可以接收字典
代码:
def demo(*args, **kwargs):print(args)print(kwargs)demo(1, 2, 3, 4, 5, name="小明", age=18, gender=True)# 需要将一个元组变量/字典变量传递给函数对应的参数
gl_nums = (1, 2, 3)
gl_xiaoming = {"name": "小明", "age": 18}# 会把 num_tuple 和 xiaoming 作为元组传递个 args
demo(*gl_nums, **gl_xiaoming)结果:

相关文章:

Python 两种多值参数
有时可能需要一个函数中处理的参数的个数是不确定的,就需要使用多值参数 参数名前加上*,代表可以接收元组参数名前加上**,代表可以接收字典 代码: def demo(*args, **kwargs):print(args)print(kwargs)demo(1, 2, 3, 4, 5, nam…...

【Python学习】Python学习19- 异常处理
目录 【Python学习】Python学习19- 异常处理 前言python标准异常异常处理带异常类型语法不带异常类型语法使用except而带多种异常类型try-finally 语句触发异常 参考 文章所属专区 Python学习 前言 本章节主要说明Python的异常处理。 python标准异常 BaseException 所有异常…...

《A++ 敏捷开发》- 4 三点估算
估算是一个范围,不是一个数 唐工:你估计完成开发用户登录模块要多少天?小李:3天。唐工:能在3天完成的可能性有多高?小李:可能性很高。唐工:可否量化一点?小李:可能性为5…...

cesiumlab切片通过arcgisjs加载
cesiumlab切片通过arcgisjs加载 需要注意2个地方,一个是tileInfo,一个是getTileUrl, 在tileInfo中定义好cesiumlab切片的相关信息。 getTileUrl 格式化url的格式。 注意设置编辑,避免超出范围报404。 <html lang"en"…...

React16源码: React中调度之scheduleWork的源码实现
scheduleWork 1 ) 概述 在 ReactDOM.render, setState, forceUpdate 这几个方法最终都调用了 scheduleWork 这个方法 在 scheduleWork 当中,它需要去找到更新对应的 FiberRoot 节点 在使用 ReactDOM.render 的时候,传给 scheduleWork 的就是…...

【STM32】| 02——常用外设 | I2C
系列文章目录 【STM32】| 01——常用外设 | USART 【STM32】| 02——常用外设 | I2C 失败了也挺可爱,成功了就超帅。 文章目录 前言1. 简介2. I2C协议2.1 I2C物理连接2.2 I2C通信协议2.2.1 起始和停止信号2.2.2 数据有效性2.2.3 数据传输格式2.2.4 从机地址/数据方…...
微服务架构设计核心理论:掌握微服务设计精髓
文章目录 一、微服务与服务治理1、概述2、Two Pizza原则和微服务团队3、主链路规划4、服务治理和微服务生命周期5、微服务架构的网络层搭建6、微服务架构的部署结构7、面试题 二、配置中心1、为什么要配置中心2、配置中心高可用思考 三、服务监控1、业务埋点的技术选型2、用户行…...

.net core 6 集成和使用 mongodb
1、安装包 MongoDB.Driver 2、定义顶层类 /// <summary> /// monggodb规范 /// </summary> public abstract class MongoDBToolBase { /// <summary> /// 客户端 /// </summary> protected MongoClient mongoClient { get; private …...
07-微服务getaway网关详解
一、初识网关 在微服务架构中,一个系统会被拆分为很多个微服务。那么作为客户端要如何去调用这么多的微服务呢?如果没有网关的存在,我们只能在客户端记录每个微服务的地址,然后分别去调用。这样的话会产生很多问题,例…...
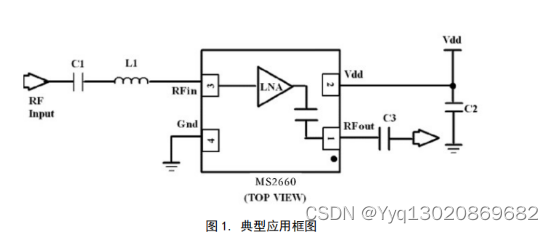
MS2660:L1 频段卫星导航射频前端低噪声放大器芯片
MS2660 是一款具有高增益、低噪声系数的低噪声放 大器(LNA)芯片,支持 L1 频段多模式全球卫星定位,可 以应用于 GPS、北斗二代、伽利略、Glonass 等 GNSS 导航 接收机中。芯片采用先进工艺制造,封装采用 2 mm 2 mm …...

微信小程序防止截屏录屏
一、使用css添加水印 使用微信小程序原生的view和css给屏幕添加水印这样可以防止用户将小程序内的隐私数据进行截图或者录屏分享导致信息泄露,给小程序添加一个水印浮层。这样即使被截图或者拍照,也能轻松地确定泄露的源头。效果图如下: 代码…...

126.(leaflet篇)leaflet松散型arcgis缓存切片加载
地图之家总目录(订阅之前必须详细了解该博客) arcgis缓存切片数据格式如下: 完整代码工程包下载,运行如有问题,可“私信”博主。效果如下所示: leaflet松散型arcgis缓存切片加载 下面献上完整代码,代码重要位置会做相应解释 <!DOCTYP...
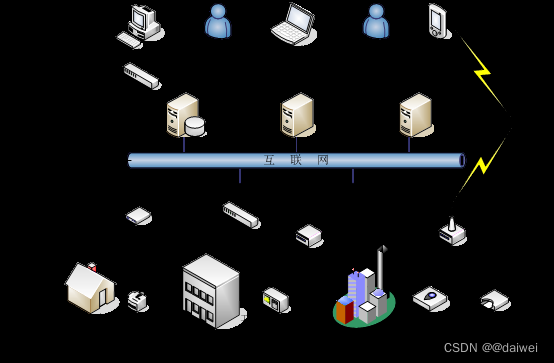
物联网介绍
阅读引言: 本文从多方面叙述物联网的定义以及在物联网当中的各种通信的介绍。 一、物联网的定义 1.1 通用的定义 物联网(Internet of Things,IOT;也称为Web of Things)是指通过各种信息传感设 备,如传感器、…...

Flume 之自定义Sink
1、简介 前文我们介绍了 Flume 如何自定义 Source, 并进行案例演示,本文将接着前文,自定义Sink,在这篇文章中,将使用自定义 Source 和 自定义的 Sink 实现数据传输,让大家快速掌握Flume这门技术。 2、自定…...
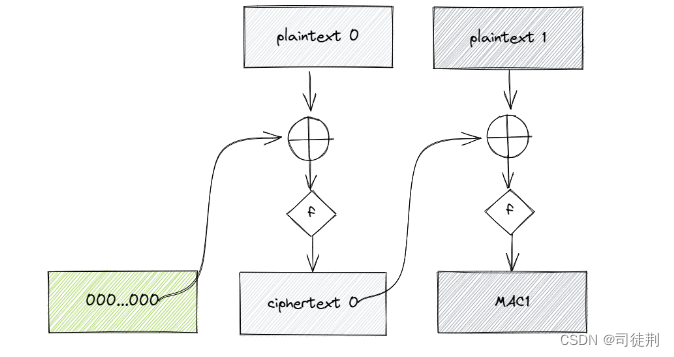
【1】SM4 CBC-MAC 机制
0x01 题目 MSG1: e55e3e24a3ae7797808fdca05a16ac15eb5fa2e6185c23a814a35ba32b4637c2 MAC1: 0712c867aa6ec7c1bb2b66312367b2c8 ----------------------------------------------------- MSG2: d8d94f33797e1f41cab9217793b2d0f02b93d46c2ead104dce4bfec453767719 MAC2: 4366…...
)
响应式编程Reactor API大全(下)
Reactor 是一个基于响应式编程的库,主要用于构建异步和事件驱动的应用程序。Reactor 提供了丰富的 API,包括创建、转换、过滤、组合等操作符,用于处理异步数据流。以下是一些 Reactor 的主要 API 示例: pom依赖 <dependencyMan…...

【STM32】HAL库的STOP低功耗模式UART串口唤醒,解决首字节出错的问题(全网第一解决方案)
【STM32】HAL库的STOP低功耗模式UART串口唤醒,解决首字节出错的问题(全网第一解决方案) 前文: 【STM32】HAL库的STOP低功耗模式UART串口唤醒,第一个接收字节出错的问题(疑难杂症) 目前已解决 …...

Python 语法糖
一、基本概念 语法糖,可以理解为:“甜蜜” 的便捷语法。 它是编程语言为程序提供的更简洁、更易读的语法实现的语法结构,它并不影响语言的功能,仅仅是一种更便捷的书写方式。 这就像你制作蛋糕时,使用现代烤箱而不是…...
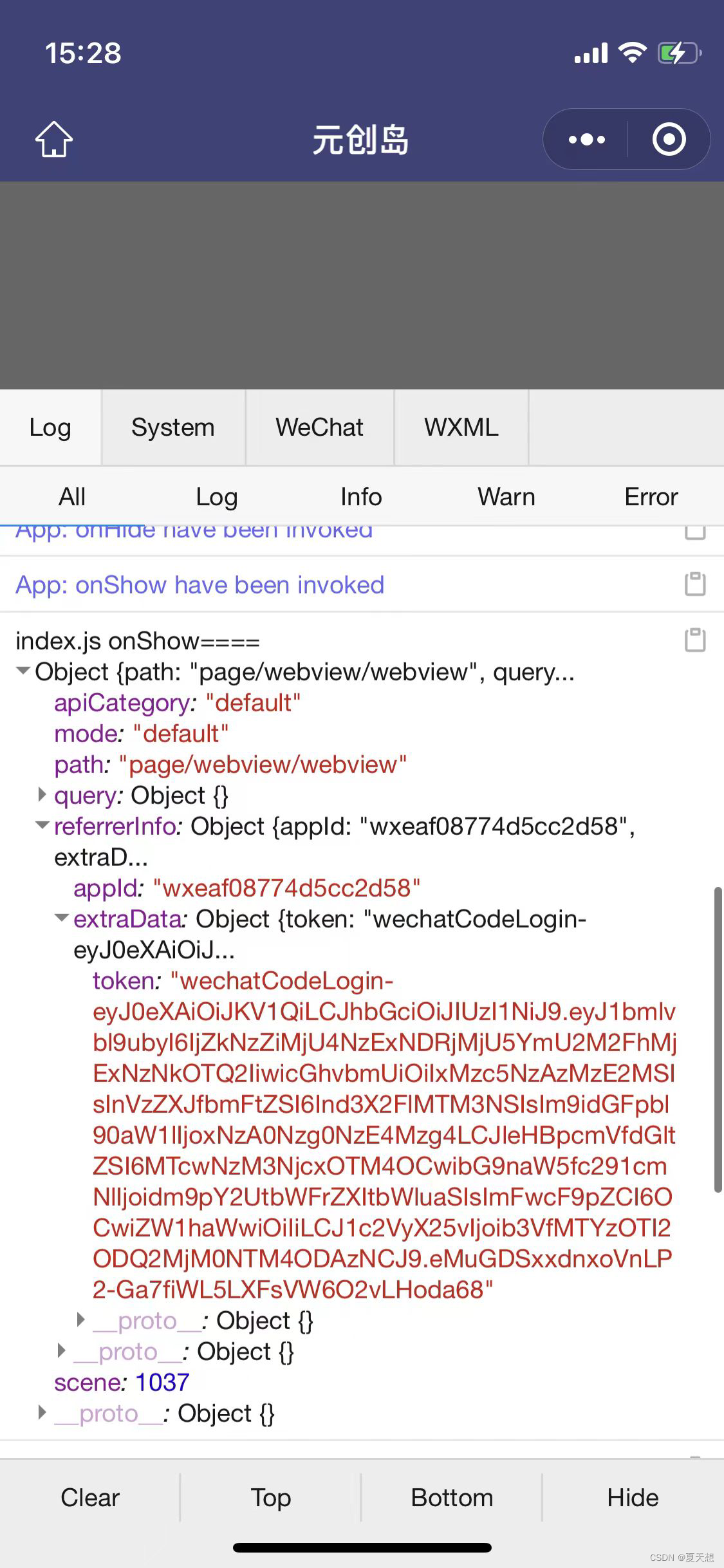
一个小程序跳转到另一个小程序中如何实现
小程序 保证两个小程序是一样的主体才可以跳转。怎么知道是不是同样的主体呢? 小程序的后台管理-设置-基本设置-基本信息。查看主体信息。 跳转 <button clicktoOtherMini()>跳转到另一个小程序</button> function toOtherMini(){wx.navigateToMini…...
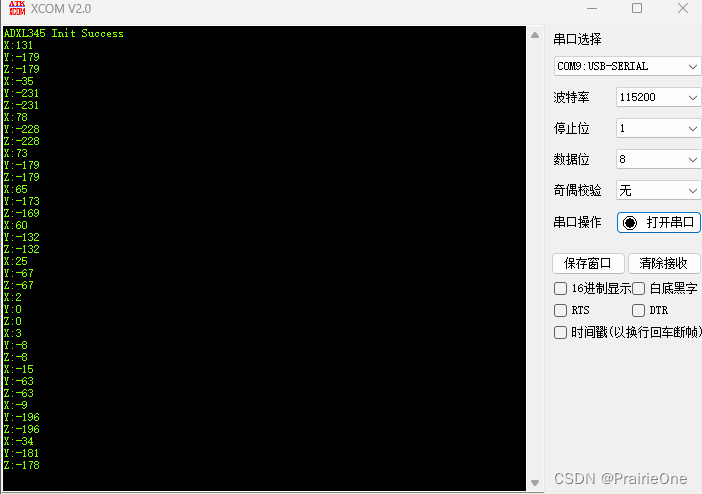
STM32+HAL库驱动ADXL345传感器(SPI协议)
STM32HAL库驱动ADXL345传感器(SPI协议) ADXL345传感器简介实物STM32CubeMX配置SPI配置片选引脚配置串口配置 特别注意(重点部分)核心代码效果展示 ADXL345传感器简介 ADXL345 是 ADI 公司推出的基于 iMEMS 技术的 3 轴、数字输出加…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
