第 7 章 排序算法
文章目录
- 7.1 排序算法的介绍
- 7.3 算法的时间复杂度
- 7.3.1 度量一个程序(算法)执行时间的两种方法
- 7.3.2 时间频度
- 7.3.3 时间复杂度
- 7.3.4 常见的时间复杂度
- 7.3.5 平均时间复杂度和最坏时间复杂度
- 7.4 算法的空间复杂度简介
- 7.4.1 基本介绍
- 7.5 冒泡排序
- 7.5.1 基本介绍
- 7.5.2 演示冒泡过程的例子(图解)
- 7.5.3 冒泡排序应用实例
- 7.6 选择排序
- 7.6.1 基本介绍
- 7.6.2 选择排序思想:
- 7.6.3 选择排序思路分析图:
- 7.6.4 选择排序应用实例:
- 7.7 插入排序
- 7.7.1 插入排序法介绍:
- 7.7.2 插入排序法思想:
- 7.7.3 插入排序思路图:
- 7.7.4 插入排序法应用实例:
- 7.8 希尔排序
- 7.8.1 简单插入排序存在的问题
- 7.8.2 希尔排序法介绍
- 7.8.3 希尔排序法基本思想
- 7.8.4 希尔排序法的示意图
- 7.8.5 希尔排序法应用实例:
- 7.9 快速排序
- 7.9.1 快速排序法介绍:
- 7.9.2 快速排序法示意图:
- 7.9.3 快速排序法应用实例:
- 7.10 归并排序
- 7.10.1 归并排序介绍:
- 7.10.2 归并排序思想示意图
- 7.10.3 归并排序思想示意
- 7.10.4 归并排序的应用实例:
- 7.11 基数排序
- 7.11.1 基数排序(桶排序)介绍:
- 7.11.2 基数排序基本思想
- 7.11.3 基数排序图文说明
- 7.11.4 基数排序代码实现
- 7.11.5 基数排序的说明:
- 7.12 常用排序算法总结和对比
- 7.12.1 一张排序算法的比较图
- 7.12.2 相关术语解释:
7.1 排序算法的介绍
排序也称排序算法(Sort Algorithm),排序是将一组数据,依指定的顺序进行排列的过程。
7.2 排序的分类:
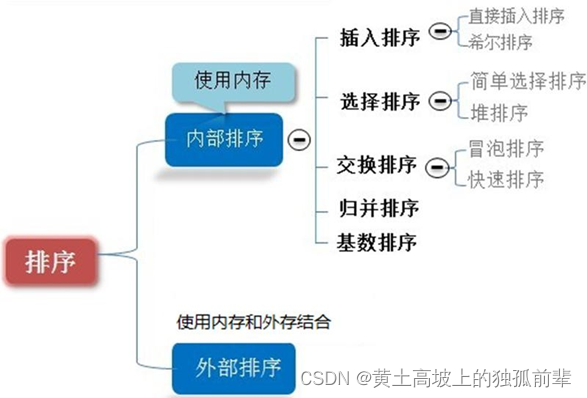
- 内部排序:
指将需要处理的所有数据都加载到内部存储器(内存)中进行排序。 - 外部排序法:
数据量过大,无法全部加载到内存中,需要借助外部存储(文件等)进行排序。 - 常见的排序算法分类(见右图):
7.3 算法的时间复杂度
7.3.1 度量一个程序(算法)执行时间的两种方法
- 事后统计的方法
这种方法可行, 但是有两个问题:一是要想对设计的算法的运行性能进行评测,需要实际运行该程序;二是所得时间的统计量依赖于计算机的硬件、软件等环境因素, 这种方式,要在同一台计算机的相同状态下运行,才能比
较那个算法速度更快。
2) 事前估算的方法
通过分析某个算法的时间复杂度来判断哪个算法更优.
7.3.2 时间频度
基本介绍
时间频度:一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为 T(n)。[举例说明]
举例说明-基本案例
比如计算 1-100 所有数字之和, 我们设计两种算法:

举例说明-忽略常数项
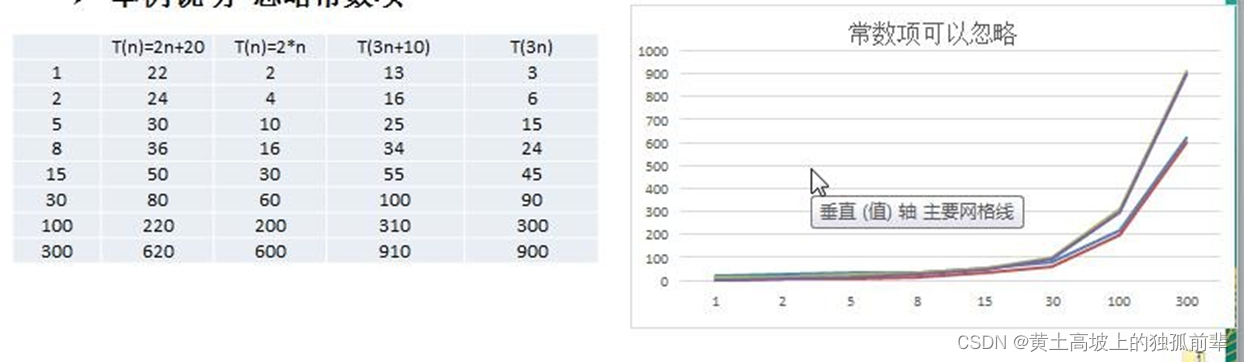
结论:
- 2n+20 和 2n 随着 n 变大,执行曲线无限接近, 20 可以忽略
- 3n+10 和 3n 随着 n 变大,执行曲线无限接近, 10 可以忽略
举例说明-忽略低次项
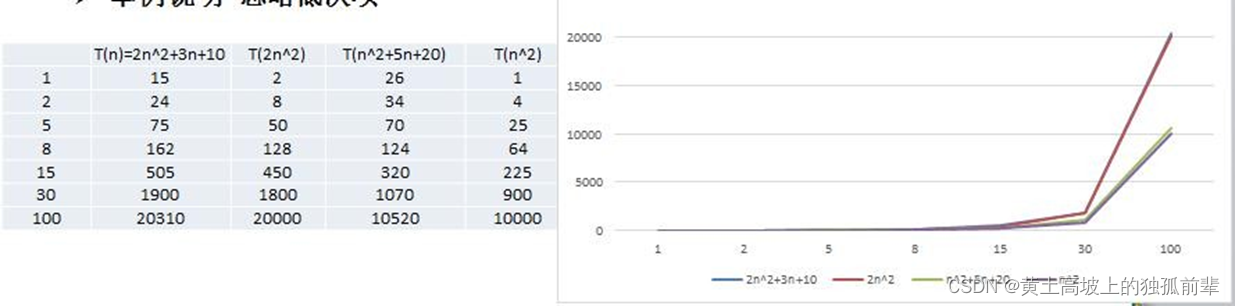
结论:
- 2n^2+3n+10 和 2n^2 随着 n 变大, 执行曲线无限接近, 可以忽略 3n+10
- n^2+5n+20 和 n^2 随着 n 变大,执行曲线无限接近, 可以忽略 5n+20
举例说明-忽略系数

结论:
- 随着 n 值变大,5n^2+7n 和 3n^2 + 2n ,执行曲线重合, 说明 这种情况下, 5 和 3 可以忽略。
- 而 n^3+5n 和 6n^3+4n ,执行曲线分离,说明多少次方式关键
7.3.3 时间复杂度
- 一般情况下,算法中的基本操作语句的重复执行次数是问题规模 n 的某个函数,用 T(n)表示,若有某个辅助函数 f(n),使得当 n 趋近于无穷大时,T(n) / f(n) 的极限值为不等于零的常数,则称 f(n)是 T(n)的同数量级函数。记作 T(n)=O( f(n) ),称O( f(n) ) 为算法的渐进时间复杂度,简称时间复杂度。
- T(n) 不同,但时间复杂度可能相同。 如:T(n)=n²+7n+6 与 T(n)=3n²+2n+2 它们的 T(n) 不同,但时间复杂度相同,都为 O(n²)。
- 计算时间复杂度的方法:
用常数 1 代替运行时间中的所有加法常数 T(n)=n²+7n+6 => T(n)=n²+7n+1
修改后的运行次数函数中,只保留最高阶项 T(n)=n²+7n+1 => T(n) = n²
去除最高阶项的系数 T(n) = n² => T(n) = n² => O(n²)
7.3.4 常见的时间复杂度
-
常数阶 O(1)
-
对数阶 O(log2n)
-
线性阶 O(n)
-
线性对数阶 O(nlog2n)
-
平方阶 O(n^2)
-
立方阶 O(n^3)
-
k 次方阶 O(n^k)
-
指数阶 O(2^n)
常见的时间复杂度对应的图:
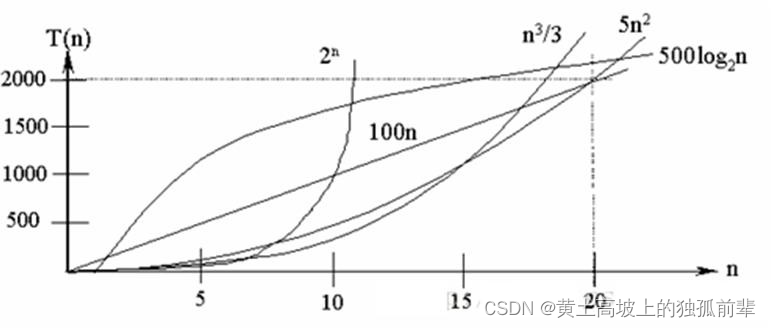
说明:
- 常见的算法时间复杂度由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)< Ο(nk) < Ο(2n) ,随着问题规模 n 的不断增大,上述时间复杂度不断增大,算法的执行效率越低
- 从图中可见,我们应该尽可能避免使用指数阶的算法
-
常数阶 O(1)

-
对数阶 O(log2n)

-
线性阶 O(n)

-
线性对数阶 O(nlogN)

-
平方阶 O(n²)

-
立方阶 O(n³)、K 次方阶 O(n^k)
说明:参考上面的 O(n²) 去理解就好了,O(n³)相当于三层 n 循环,其它的类似
7.3.5 平均时间复杂度和最坏时间复杂度
- 平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下,该算法的运行时间。
- 最坏情况下的时间复杂度称最坏时间复杂度。一般讨论的时间复杂度均是最坏情况下的时间复杂度。这样做的原因是:最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限,这就保证了算法的运行时间不会比最坏情况更长。
- 平均时间复杂度和最坏时间复杂度是否一致,和算法有关(如图:)。
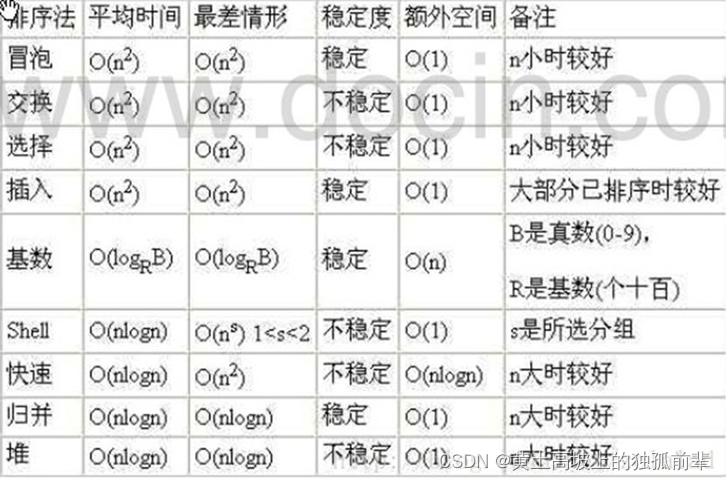
7.4 算法的空间复杂度简介
7.4.1 基本介绍
- 类似于时间复杂度的讨论,一个算法的空间复杂度(Space Complexity)定义为该算法所耗费的存储空间,它也是问题规模 n 的函数。
- 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模 n 有关,它随着 n 的增大而增大,当 n 较大时,将占用较多的存储单元,例如快速排序和归并排序算法, 基数排序就属于这种情况
- 在做算法分析时,主要讨论的是时间复杂度。从用户使用体验上看,更看重的程序执行的速度。一些缓存产品
(redis, memcache)和算法(基数排序)本质就是用空间换时间.
7.5 冒泡排序
7.5.1 基本介绍
冒泡排序(Bubble Sorting)的基本思想是:通过对待排序序列从前向后(从下标较小的元素开始),依次比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就象水底下的气泡一样逐渐向上冒。
优化:
因为排序的过程中,各元素不断接近自己的位置,如果一趟比较下来没有进行过交换,就说明序列有序,因此要在排序过程中设置一个标志 flag 判断元素是否进行过交换。从而减少不必要的比较。(这里说的优化,可以在冒泡排序写好后,在进行)
7.5.2 演示冒泡过程的例子(图解)

小结上面的图解过程:
(1) 一共进行 数组的大小-1 次 大的循环
(2) 每一趟排序的次数在逐渐的减少
(3) 如果我们发现在某趟排序中,没有发生一次交换, 可以提前结束冒泡排序。这个就是优化
7.5.3 冒泡排序应用实例
我们举一个具体的案例来说明冒泡法。我们将五个无序的数:3, 9, -1, 10, -2 使用冒泡排序法将其排成一个从小到大的有序数列。
代码实现:
package com.atguigu.sort;import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;public class BubbleSort {public static void main(String[] args) {
// int arr[] = {3, 9, -1, 10, 20};
//
// System.out.println("排序前");
// System.out.println(Arrays.toString(arr));//为了容量理解,我们把冒泡排序的演变过程,给大家展示//测试一下冒泡排序的速度O(n^2), 给80000个数据,测试//创建要给80000个的随机的数组int[] arr = new int[80000];for(int i =0; i < 80000;i++) {arr[i] = (int)(Math.random() * 8000000); //生成一个[0, 8000000) 数}Date data1 = new Date();SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");String date1Str = simpleDateFormat.format(data1);System.out.println("排序前的时间是=" + date1Str);//测试冒泡排序bubbleSort(arr);Date data2 = new Date();String date2Str = simpleDateFormat.format(data2);System.out.println("排序后的时间是=" + date2Str);//System.out.println("排序后");//System.out.println(Arrays.toString(arr));/*// 第二趟排序,就是将第二大的数排在倒数第二位for (int j = 0; j < arr.length - 1 - 1 ; j++) {// 如果前面的数比后面的数大,则交换if (arr[j] > arr[j + 1]) {temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}System.out.println("第二趟排序后的数组");System.out.println(Arrays.toString(arr));// 第三趟排序,就是将第三大的数排在倒数第三位for (int j = 0; j < arr.length - 1 - 2; j++) {// 如果前面的数比后面的数大,则交换if (arr[j] > arr[j + 1]) {temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}System.out.println("第三趟排序后的数组");System.out.println(Arrays.toString(arr));// 第四趟排序,就是将第4大的数排在倒数第4位for (int j = 0; j < arr.length - 1 - 3; j++) {// 如果前面的数比后面的数大,则交换if (arr[j] > arr[j + 1]) {temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}System.out.println("第四趟排序后的数组");System.out.println(Arrays.toString(arr)); */}// 将前面额冒泡排序算法,封装成一个方法public static void bubbleSort(int[] arr) {// 冒泡排序 的时间复杂度 O(n^2), 自己写出int temp = 0; // 临时变量boolean flag = false; // 标识变量,表示是否进行过交换for (int i = 0; i < arr.length - 1; i++) {for (int j = 0; j < arr.length - 1 - i; j++) {// 如果前面的数比后面的数大,则交换if (arr[j] > arr[j + 1]) {flag = true;temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}//System.out.println("第" + (i + 1) + "趟排序后的数组");//System.out.println(Arrays.toString(arr));if (!flag) { // 在一趟排序中,一次交换都没有发生过break;} else {flag = false; // 重置flag!!!, 进行下次判断}}}}
7.6 选择排序
7.6.1 基本介绍
选择式排序也属于内部排序法,是从欲排序的数据中,按指定的规则选出某一元素,再依规定交换位置后达到排序的目的。
7.6.2 选择排序思想:
选择排序(select sorting)也是一种简单的排序方法。它的基本思想是:第一次从 arr[0]~arr[n-1]中选取最小值,与 arr[0]交换,第二次从 arr[1]~arr[n-1]中选取最小值,与 arr[1]交换,第三次从 arr[2]~arr[n-1]中选取最小值,与 arr[2]交换,…,第 i 次从 arr[i-1]~arr[n-1]中选取最小值,与 arr[i-1]交换,…, 第 n-1 次从 arr[n-2]~arr[n-1]中选取最小值,与 arr[n-2]交换,总共通过 n-1 次,得到一个按排序码从小到大排列的有序序列。
7.6.3 选择排序思路分析图:
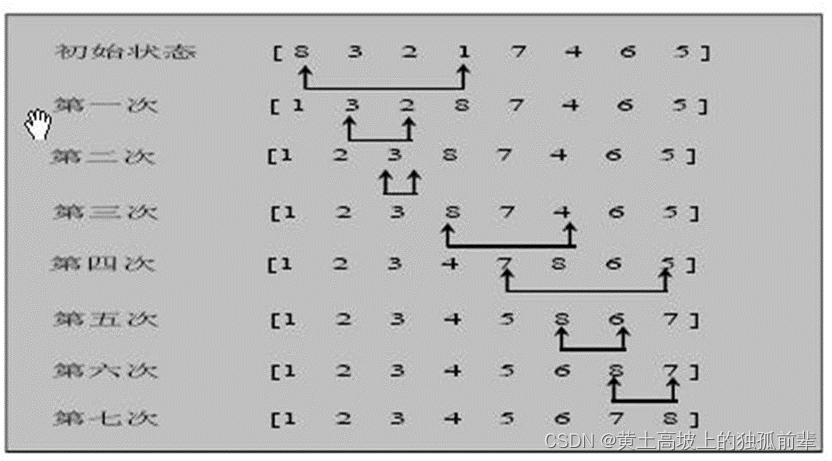
对一个数组的选择排序再进行讲解

7.6.4 选择排序应用实例:
有一群牛 , 颜值分别是 101, 34, 119, 1 请使用选择排序从低到高进行排序 [101, 34, 119, 1]

代码实现
package com.atguigu.sort;import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
//选择排序
public class SelectSort {public static void main(String[] args) {//int [] arr = {101, 34, 119, 1, -1, 90, 123};//创建要给80000个的随机的数组int[] arr = new int[80000];for (int i = 0; i < 80000; i++) {arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数}System.out.println("排序前");//System.out.println(Arrays.toString(arr));Date data1 = new Date();SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");String date1Str = simpleDateFormat.format(data1);System.out.println("排序前的时间是=" + date1Str);selectSort(arr);Date data2 = new Date();String date2Str = simpleDateFormat.format(data2);System.out.println("排序前的时间是=" + date2Str);//System.out.println("排序后");//System.out.println(Arrays.toString(arr));}//选择排序public static void selectSort(int[] arr) {//在推导的过程,我们发现了规律,因此,可以使用for来解决//选择排序时间复杂度是 O(n^2)for (int i = 0; i < arr.length - 1; i++) {int minIndex = i;int min = arr[i];for (int j = i + 1; j < arr.length; j++) {if (min > arr[j]) { // 说明假定的最小值,并不是最小min = arr[j]; // 重置minminIndex = j; // 重置minIndex}}// 将最小值,放在arr[0], 即交换if (minIndex != i) {arr[minIndex] = arr[i];arr[i] = min;}//System.out.println("第"+(i+1)+"轮后~~");//System.out.println(Arrays.toString(arr));// 1, 34, 119, 101}/*//使用逐步推导的方式来,讲解选择排序//第1轮//原始的数组 : 101, 34, 119, 1//第一轮排序 : 1, 34, 119, 101//算法 先简单--》 做复杂, 就是可以把一个复杂的算法,拆分成简单的问题-》逐步解决//第1轮int minIndex = 0;int min = arr[0];for(int j = 0 + 1; j < arr.length; j++) {if (min > arr[j]) { //说明假定的最小值,并不是最小min = arr[j]; //重置minminIndex = j; //重置minIndex}}//将最小值,放在arr[0], 即交换if(minIndex != 0) {arr[minIndex] = arr[0];arr[0] = min;}System.out.println("第1轮后~~");System.out.println(Arrays.toString(arr));// 1, 34, 119, 101//第2轮minIndex = 1;min = arr[1];for (int j = 1 + 1; j < arr.length; j++) {if (min > arr[j]) { // 说明假定的最小值,并不是最小min = arr[j]; // 重置minminIndex = j; // 重置minIndex}}// 将最小值,放在arr[0], 即交换if(minIndex != 1) {arr[minIndex] = arr[1];arr[1] = min;}System.out.println("第2轮后~~");System.out.println(Arrays.toString(arr));// 1, 34, 119, 101//第3轮minIndex = 2;min = arr[2];for (int j = 2 + 1; j < arr.length; j++) {if (min > arr[j]) { // 说明假定的最小值,并不是最小min = arr[j]; // 重置minminIndex = j; // 重置minIndex}}// 将最小值,放在arr[0], 即交换if (minIndex != 2) {arr[minIndex] = arr[2];arr[2] = min;}System.out.println("第3轮后~~");System.out.println(Arrays.toString(arr));// 1, 34, 101, 119 */}}
7.7 插入排序
7.7.1 插入排序法介绍:
插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的。
7.7.2 插入排序法思想:
插入排序(Insertion Sorting)的基本思想是:把 n 个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有 n-1 个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
7.7.3 插入排序思路图:
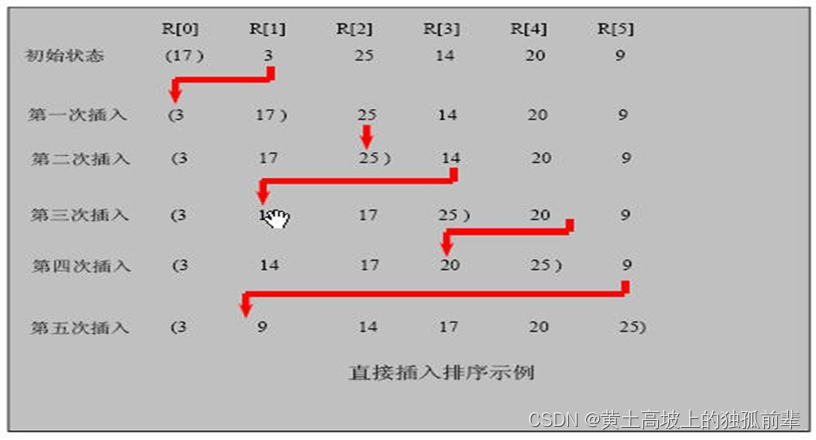
7.7.4 插入排序法应用实例:
有一群小牛, 考试成绩分别是 101, 34, 119, 1 请从小到大排序代码实现:
package com.atguigu.sort;import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;public class InsertSort {public static void main(String[] args) {//int[] arr = {101, 34, 119, 1, -1, 89}; // 创建要给80000个的随机的数组int[] arr = new int[80000];for (int i = 0; i < 80000; i++) {arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数}System.out.println("插入排序前");Date data1 = new Date();SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");String date1Str = simpleDateFormat.format(data1);System.out.println("排序前的时间是=" + date1Str);insertSort(arr); //调用插入排序算法Date data2 = new Date();String date2Str = simpleDateFormat.format(data2);System.out.println("排序前的时间是=" + date2Str);//System.out.println(Arrays.toString(arr));}//插入排序public static void insertSort(int[] arr) {int insertVal = 0;int insertIndex = 0;//使用for循环来把代码简化for(int i = 1; i < arr.length; i++) {//定义待插入的数insertVal = arr[i];insertIndex = i - 1; // 即arr[1]的前面这个数的下标// 给insertVal 找到插入的位置// 说明// 1. insertIndex >= 0 保证在给insertVal 找插入位置,不越界// 2. insertVal < arr[insertIndex] 待插入的数,还没有找到插入位置// 3. 就需要将 arr[insertIndex] 后移while (insertIndex >= 0 && insertVal < arr[insertIndex]) {arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]insertIndex--;}// 当退出while循环时,说明插入的位置找到, insertIndex + 1// 举例:理解不了,我们一会 debug//这里我们判断是否需要赋值if(insertIndex + 1 != i) {arr[insertIndex + 1] = insertVal;}//System.out.println("第"+i+"轮插入");//System.out.println(Arrays.toString(arr));}/*//使用逐步推导的方式来讲解,便利理解//第1轮 {101, 34, 119, 1}; => {34, 101, 119, 1}//{101, 34, 119, 1}; => {101,101,119,1}//定义待插入的数int insertVal = arr[1];int insertIndex = 1 - 1; //即arr[1]的前面这个数的下标//给insertVal 找到插入的位置//说明//1. insertIndex >= 0 保证在给insertVal 找插入位置,不越界//2. insertVal < arr[insertIndex] 待插入的数,还没有找到插入位置//3. 就需要将 arr[insertIndex] 后移while(insertIndex >= 0 && insertVal < arr[insertIndex] ) {arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]insertIndex--;}//当退出while循环时,说明插入的位置找到, insertIndex + 1//举例:理解不了,我们一会 debugarr[insertIndex + 1] = insertVal;System.out.println("第1轮插入");System.out.println(Arrays.toString(arr));//第2轮insertVal = arr[2];insertIndex = 2 - 1; while(insertIndex >= 0 && insertVal < arr[insertIndex] ) {arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]insertIndex--;}arr[insertIndex + 1] = insertVal;System.out.println("第2轮插入");System.out.println(Arrays.toString(arr));//第3轮insertVal = arr[3];insertIndex = 3 - 1;while (insertIndex >= 0 && insertVal < arr[insertIndex]) {arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]insertIndex--;}arr[insertIndex + 1] = insertVal;System.out.println("第3轮插入");System.out.println(Arrays.toString(arr)); */}}
7.8 希尔排序
7.8.1 简单插入排序存在的问题
我们看简单的插入排序可能存在的问题.
数组 arr = {2,3,4,5,6,1} 这时需要插入的数 1(最小), 这样的过程是:
{2,3,4,5,6,6}
{2,3,4,5,5,6}
{2,3,4,4,5,6}
{2,3,3,4,5,6}
{2,2,3,4,5,6}
{1,2,3,4,5,6}
结论: 当需要插入的数是较小的数时,后移的次数明显增多,对效率有影响.
7.8.2 希尔排序法介绍
希尔排序是希尔(Donald Shell)于 1959 年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入
排序经过改进之后的一个更高效的版本,也称为缩小增量排序。
7.8.3 希尔排序法基本思想
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个文件恰被分成一组,算法便终止
7.8.4 希尔排序法的示意图

7.8.5 希尔排序法应用实例:
有一群小牛, 考试成绩分别是 {8,9,1,7,2,3,5,4,6,0} 请从小到大排序. 请分别使用
-
希尔排序时, 对有序序列在插入时采用交换法, 并测试排序速度.
-
希尔排序时, 对有序序列在插入时采用移动法, 并测试排序速度
-
代码实现
package com.atguigu.sort;import java.text.SimpleDateFormat; import java.util.Arrays; import java.util.Date;public class ShellSort {public static void main(String[] args) {//int[] arr = { 8, 9, 1, 7, 2, 3, 5, 4, 6, 0 };// 创建要给80000个的随机的数组int[] arr = new int[8000000];for (int i = 0; i < 8000000; i++) {arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数}System.out.println("排序前");Date data1 = new Date();SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");String date1Str = simpleDateFormat.format(data1);System.out.println("排序前的时间是=" + date1Str);//shellSort(arr); //交换式shellSort2(arr);//移位方式Date data2 = new Date();String date2Str = simpleDateFormat.format(data2);System.out.println("排序前的时间是=" + date2Str);//System.out.println(Arrays.toString(arr));}// 使用逐步推导的方式来编写希尔排序// 希尔排序时, 对有序序列在插入时采用交换法, // 思路(算法) ===> 代码public static void shellSort(int[] arr) {int temp = 0;int count = 0;// 根据前面的逐步分析,使用循环处理for (int gap = arr.length / 2; gap > 0; gap /= 2) {for (int i = gap; i < arr.length; i++) {// 遍历各组中所有的元素(共gap组,每组有个元素), 步长gapfor (int j = i - gap; j >= 0; j -= gap) {// 如果当前元素大于加上步长后的那个元素,说明交换if (arr[j] > arr[j + gap]) {temp = arr[j];arr[j] = arr[j + gap];arr[j + gap] = temp;}}}//System.out.println("希尔排序第" + (++count) + "轮 =" + Arrays.toString(arr));}/*// 希尔排序的第1轮排序// 因为第1轮排序,是将10个数据分成了 5组for (int i = 5; i < arr.length; i++) {// 遍历各组中所有的元素(共5组,每组有2个元素), 步长5for (int j = i - 5; j >= 0; j -= 5) {// 如果当前元素大于加上步长后的那个元素,说明交换if (arr[j] > arr[j + 5]) {temp = arr[j];arr[j] = arr[j + 5];arr[j + 5] = temp;}}}System.out.println("希尔排序1轮后=" + Arrays.toString(arr));//// 希尔排序的第2轮排序// 因为第2轮排序,是将10个数据分成了 5/2 = 2组for (int i = 2; i < arr.length; i++) {// 遍历各组中所有的元素(共5组,每组有2个元素), 步长5for (int j = i - 2; j >= 0; j -= 2) {// 如果当前元素大于加上步长后的那个元素,说明交换if (arr[j] > arr[j + 2]) {temp = arr[j];arr[j] = arr[j + 2];arr[j + 2] = temp;}}}System.out.println("希尔排序2轮后=" + Arrays.toString(arr));//// 希尔排序的第3轮排序// 因为第3轮排序,是将10个数据分成了 2/2 = 1组for (int i = 1; i < arr.length; i++) {// 遍历各组中所有的元素(共5组,每组有2个元素), 步长5for (int j = i - 1; j >= 0; j -= 1) {// 如果当前元素大于加上步长后的那个元素,说明交换if (arr[j] > arr[j + 1]) {temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}System.out.println("希尔排序3轮后=" + Arrays.toString(arr));//*/}//对交换式的希尔排序进行优化->移位法public static void shellSort2(int[] arr) {// 增量gap, 并逐步的缩小增量for (int gap = arr.length / 2; gap > 0; gap /= 2) {// 从第gap个元素,逐个对其所在的组进行直接插入排序for (int i = gap; i < arr.length; i++) {int j = i;int temp = arr[j];if (arr[j] < arr[j - gap]) {while (j - gap >= 0 && temp < arr[j - gap]) {//移动arr[j] = arr[j-gap];j -= gap;}//当退出while后,就给temp找到插入的位置arr[j] = temp;}}}}}
7.9 快速排序
7.9.1 快速排序法介绍:
快速排序(Quicksort)是对冒泡排序的一种改进。基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
7.9.2 快速排序法示意图:

7.9.3 快速排序法应用实例:
要求: 对 [-9,78,0,23,-567,70] 进行从小到大的排序,要求使用快速排序法。【测试 8w 和 800w】说明[验证分析]:
-
如果取消左右递归,结果是 -9 -567 0 23 78 70
-
如果取消右递归,结果是 -567 -9 0 23 78 70
-
如果取消左递归,结果是 -9 -567 0 23 70 78
-
代码实现
package com.atguigu.sort;import java.text.SimpleDateFormat; import java.util.Arrays; import java.util.Date;public class QuickSort {public static void main(String[] args) {//int[] arr = {-9,78,0,23,-567,70, -1,900, 4561};//测试快排的执行速度// 创建要给80000个的随机的数组int[] arr = new int[8000000];for (int i = 0; i < 8000000; i++) {arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数}System.out.println("排序前");Date data1 = new Date();SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");String date1Str = simpleDateFormat.format(data1);System.out.println("排序前的时间是=" + date1Str);quickSort(arr, 0, arr.length-1);Date data2 = new Date();String date2Str = simpleDateFormat.format(data2);System.out.println("排序前的时间是=" + date2Str);//System.out.println("arr=" + Arrays.toString(arr));}public static void quickSort(int[] arr,int left, int right) {int l = left; //左下标int r = right; //右下标//pivot 中轴值int pivot = arr[(left + right) / 2];int temp = 0; //临时变量,作为交换时使用//while循环的目的是让比pivot 值小放到左边//比pivot 值大放到右边while( l < r) { //在pivot的左边一直找,找到大于等于pivot值,才退出while( arr[l] < pivot) {l += 1;}//在pivot的右边一直找,找到小于等于pivot值,才退出while(arr[r] > pivot) {r -= 1;}//如果l >= r说明pivot 的左右两的值,已经按照左边全部是//小于等于pivot值,右边全部是大于等于pivot值if( l >= r) {break;}//交换temp = arr[l];arr[l] = arr[r];arr[r] = temp;//如果交换完后,发现这个arr[l] == pivot值 相等 r--, 前移if(arr[l] == pivot) {r -= 1;}//如果交换完后,发现这个arr[r] == pivot值 相等 l++, 后移if(arr[r] == pivot) {l += 1;}}// 如果 l == r, 必须l++, r--, 否则为出现栈溢出if (l == r) {l += 1;r -= 1;}//向左递归if(left < r) {quickSort(arr, left, r);}//向右递归if(right > l) {quickSort(arr, l, right);}} }
7.10 归并排序
7.10.1 归并排序介绍:
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
7.10.2 归并排序思想示意图
1-基本思想:
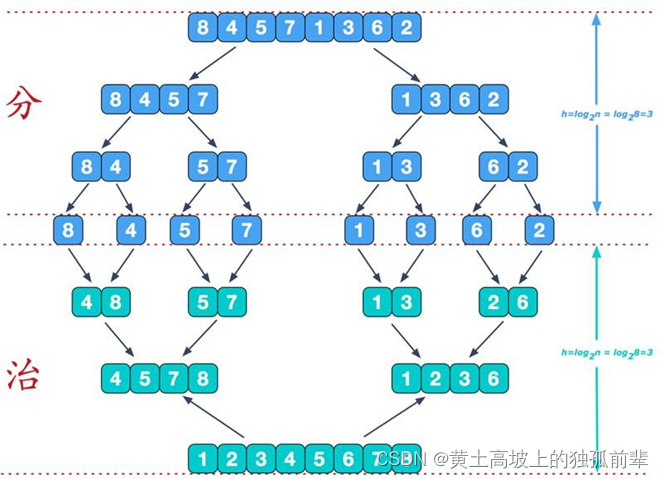
7.10.3 归并排序思想示意
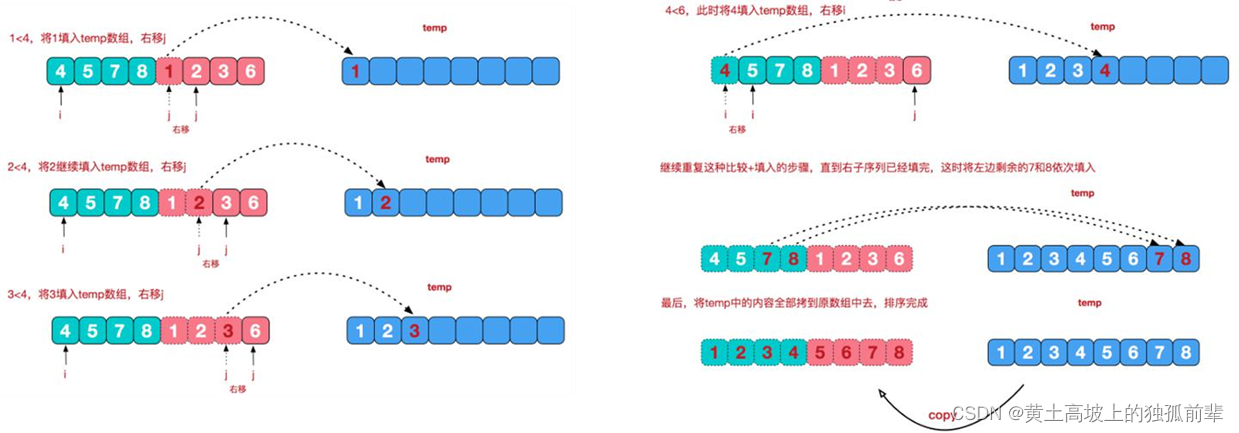
图 2-合并相邻有序子序列:
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将
[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤
7.10.4 归并排序的应用实例:
给你一个数组, val arr = Array(8, 4, 5, 7, 1, 3, 6, 2 ), 请使用归并排序完成排序。
代码演示:
package com.atguigu.sort;import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;public class MergetSort {public static void main(String[] args) {//int arr[] = { 8, 4, 5, 7, 1, 3, 6, 2 }; ////测试快排的执行速度// 创建要给80000个的随机的数组int[] arr = new int[8000000];for (int i = 0; i < 8000000; i++) {arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数}System.out.println("排序前");Date data1 = new Date();SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");String date1Str = simpleDateFormat.format(data1);System.out.println("排序前的时间是=" + date1Str);int temp[] = new int[arr.length]; //归并排序需要一个额外空间mergeSort(arr, 0, arr.length - 1, temp);Date data2 = new Date();String date2Str = simpleDateFormat.format(data2);System.out.println("排序前的时间是=" + date2Str);//System.out.println("归并排序后=" + Arrays.toString(arr));}//分+合方法public static void mergeSort(int[] arr, int left, int right, int[] temp) {if(left < right) {int mid = (left + right) / 2; //中间索引//向左递归进行分解mergeSort(arr, left, mid, temp);//向右递归进行分解mergeSort(arr, mid + 1, right, temp);//合并merge(arr, left, mid, right, temp);}}//合并的方法/*** * @param arr 排序的原始数组* @param left 左边有序序列的初始索引* @param mid 中间索引* @param right 右边索引* @param temp 做中转的数组*/public static void merge(int[] arr, int left, int mid, int right, int[] temp) {int i = left; // 初始化i, 左边有序序列的初始索引int j = mid + 1; //初始化j, 右边有序序列的初始索引int t = 0; // 指向temp数组的当前索引//(一)//先把左右两边(有序)的数据按照规则填充到temp数组//直到左右两边的有序序列,有一边处理完毕为止while (i <= mid && j <= right) {//继续//如果左边的有序序列的当前元素,小于等于右边有序序列的当前元素//即将左边的当前元素,填充到 temp数组 //然后 t++, i++if(arr[i] <= arr[j]) {temp[t] = arr[i];t += 1;i += 1;} else { //反之,将右边有序序列的当前元素,填充到temp数组temp[t] = arr[j];t += 1;j += 1;}}//(二)//把有剩余数据的一边的数据依次全部填充到tempwhile( i <= mid) { //左边的有序序列还有剩余的元素,就全部填充到temptemp[t] = arr[i];t += 1;i += 1; }while( j <= right) { //右边的有序序列还有剩余的元素,就全部填充到temptemp[t] = arr[j];t += 1;j += 1; }//(三)//将temp数组的元素拷贝到arr//注意,并不是每次都拷贝所有t = 0;int tempLeft = left; // //第一次合并 tempLeft = 0 , right = 1 // tempLeft = 2 right = 3 // tL=0 ri=3//最后一次 tempLeft = 0 right = 7while(tempLeft <= right) { arr[tempLeft] = temp[t];t += 1;tempLeft += 1;}}}
7.11 基数排序
7.11.1 基数排序(桶排序)介绍:
- 基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或 bin sort,顾名思义,它是通过键值的各个位的值,将要排序的元素分配至某些“桶”中,达到排序的作用
- 基数排序法是属于稳定性的排序,基数排序法的是效率高的稳定性排序法
- 基数排序(Radix Sort)是桶排序的扩展
- 基数排序是 1887 年赫尔曼·何乐礼发明的。它是这样实现的:将整数按位数切割成不同的数字,然后按每个位数分别比较。
7.11.2 基数排序基本思想
-
将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
-
这样说明,比较难理解,下面我们看一个图文解释,理解基数排序的步骤
7.11.3 基数排序图文说明
将数组 {53, 3, 542, 748, 14, 214} 使用基数排序, 进行升序排序

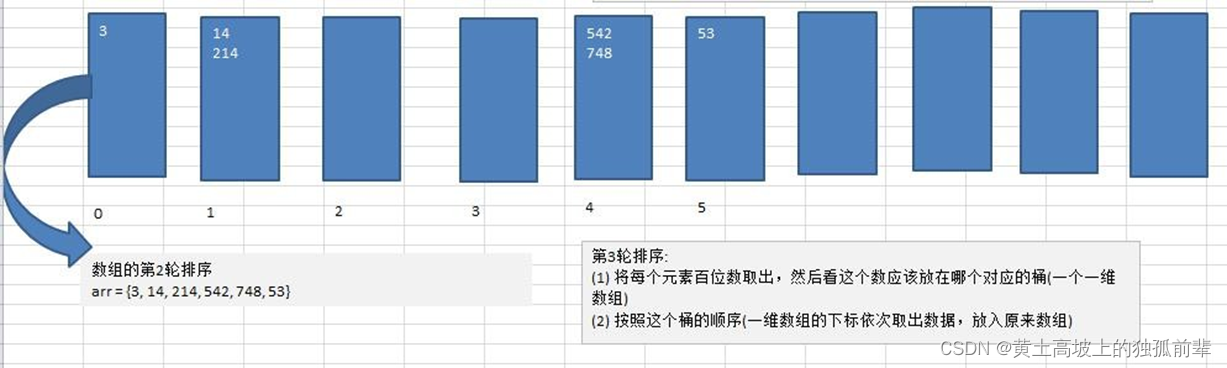
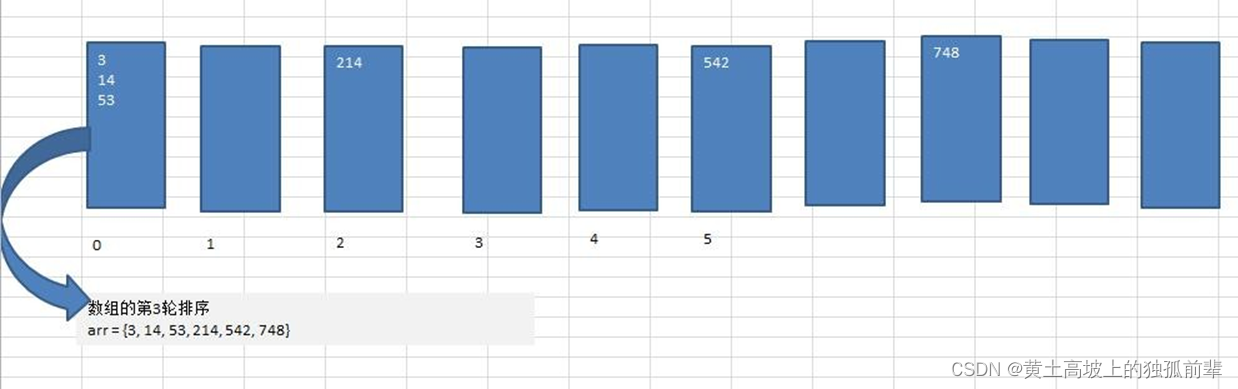
7.11.4 基数排序代码实现
要求:将数组 {53, 3, 542, 748, 14, 214} 使用基数排序, 进行升序排序
-
思路分析:前面的图文已经讲明确
-
代码实现:
package com.atguigu.sort;import java.text.SimpleDateFormat; import java.util.Arrays; import java.util.Date;public class RadixSort {public static void main(String[] args) {int arr[] = { 53, 3, 542, 748, 14, 214};// 80000000 * 11 * 4 / 1024 / 1024 / 1024 =3.3G // int[] arr = new int[8000000]; // for (int i = 0; i < 8000000; i++) { // arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数 // }System.out.println("排序前");Date data1 = new Date();SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");String date1Str = simpleDateFormat.format(data1);System.out.println("排序前的时间是=" + date1Str);radixSort(arr);Date data2 = new Date();String date2Str = simpleDateFormat.format(data2);System.out.println("排序前的时间是=" + date2Str);System.out.println("基数排序后 " + Arrays.toString(arr));}//基数排序方法public static void radixSort(int[] arr) {//根据前面的推导过程,我们可以得到最终的基数排序代码//1. 得到数组中最大的数的位数int max = arr[0]; //假设第一数就是最大数for(int i = 1; i < arr.length; i++) {if (arr[i] > max) {max = arr[i];}}//得到最大数是几位数int maxLength = (max + "").length();//定义一个二维数组,表示10个桶, 每个桶就是一个一维数组//说明//1. 二维数组包含10个一维数组//2. 为了防止在放入数的时候,数据溢出,则每个一维数组(桶),大小定为arr.length//3. 名明确,基数排序是使用空间换时间的经典算法int[][] bucket = new int[10][arr.length];//为了记录每个桶中,实际存放了多少个数据,我们定义一个一维数组来记录各个桶的每次放入的数据个数//可以这里理解//比如:bucketElementCounts[0] , 记录的就是 bucket[0] 桶的放入数据个数int[] bucketElementCounts = new int[10];//这里我们使用循环将代码处理for(int i = 0 , n = 1; i < maxLength; i++, n *= 10) {//(针对每个元素的对应位进行排序处理), 第一次是个位,第二次是十位,第三次是百位..for(int j = 0; j < arr.length; j++) {//取出每个元素的对应位的值int digitOfElement = arr[j] / n % 10;//放入到对应的桶中bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];bucketElementCounts[digitOfElement]++;}//按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)int index = 0;//遍历每一桶,并将桶中是数据,放入到原数组for(int k = 0; k < bucketElementCounts.length; k++) {//如果桶中,有数据,我们才放入到原数组if(bucketElementCounts[k] != 0) {//循环该桶即第k个桶(即第k个一维数组), 放入for(int l = 0; l < bucketElementCounts[k]; l++) {//取出元素放入到arrarr[index++] = bucket[k][l];}}//第i+1轮处理后,需要将每个 bucketElementCounts[k] = 0 !!!!bucketElementCounts[k] = 0;}//System.out.println("第"+(i+1)+"轮,对个位的排序处理 arr =" + Arrays.toString(arr));}/*//第1轮(针对每个元素的个位进行排序处理)for(int j = 0; j < arr.length; j++) {//取出每个元素的个位的值int digitOfElement = arr[j] / 1 % 10;//放入到对应的桶中bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];bucketElementCounts[digitOfElement]++;}//按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)int index = 0;//遍历每一桶,并将桶中是数据,放入到原数组for(int k = 0; k < bucketElementCounts.length; k++) {//如果桶中,有数据,我们才放入到原数组if(bucketElementCounts[k] != 0) {//循环该桶即第k个桶(即第k个一维数组), 放入for(int l = 0; l < bucketElementCounts[k]; l++) {//取出元素放入到arrarr[index++] = bucket[k][l];}}//第l轮处理后,需要将每个 bucketElementCounts[k] = 0 !!!!bucketElementCounts[k] = 0;}System.out.println("第1轮,对个位的排序处理 arr =" + Arrays.toString(arr));//==========================================//第2轮(针对每个元素的十位进行排序处理)for (int j = 0; j < arr.length; j++) {// 取出每个元素的十位的值int digitOfElement = arr[j] / 10 % 10; //748 / 10 => 74 % 10 => 4// 放入到对应的桶中bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];bucketElementCounts[digitOfElement]++;}// 按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)index = 0;// 遍历每一桶,并将桶中是数据,放入到原数组for (int k = 0; k < bucketElementCounts.length; k++) {// 如果桶中,有数据,我们才放入到原数组if (bucketElementCounts[k] != 0) {// 循环该桶即第k个桶(即第k个一维数组), 放入for (int l = 0; l < bucketElementCounts[k]; l++) {// 取出元素放入到arrarr[index++] = bucket[k][l];}}//第2轮处理后,需要将每个 bucketElementCounts[k] = 0 !!!!bucketElementCounts[k] = 0;}System.out.println("第2轮,对个位的排序处理 arr =" + Arrays.toString(arr));//第3轮(针对每个元素的百位进行排序处理)for (int j = 0; j < arr.length; j++) {// 取出每个元素的百位的值int digitOfElement = arr[j] / 100 % 10; // 748 / 100 => 7 % 10 = 7// 放入到对应的桶中bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];bucketElementCounts[digitOfElement]++;}// 按照这个桶的顺序(一维数组的下标依次取出数据,放入原来数组)index = 0;// 遍历每一桶,并将桶中是数据,放入到原数组for (int k = 0; k < bucketElementCounts.length; k++) {// 如果桶中,有数据,我们才放入到原数组if (bucketElementCounts[k] != 0) {// 循环该桶即第k个桶(即第k个一维数组), 放入for (int l = 0; l < bucketElementCounts[k]; l++) {// 取出元素放入到arrarr[index++] = bucket[k][l];}}//第3轮处理后,需要将每个 bucketElementCounts[k] = 0 !!!!bucketElementCounts[k] = 0;}System.out.println("第3轮,对个位的排序处理 arr =" + Arrays.toString(arr)); */} }
7.11.5 基数排序的说明:
- 基数排序是对传统桶排序的扩展,速度很快.
- 基数排序是经典的空间换时间的方式,占用内存很大, 当对海量数据排序时,容易造成 OutOfMemoryError 。
- 基数排序时稳定的。[注:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且 r[i]在 r[j]之前,而在排序后的序列中,r[i]仍在 r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的]
- 有负数的数组,我们不用基数排序来进行排序, 如果要支持负数,参考: https://code.i-harness.com/zh-CN/q/e98fa9
7.12 常用排序算法总结和对比
7.12.1 一张排序算法的比较图
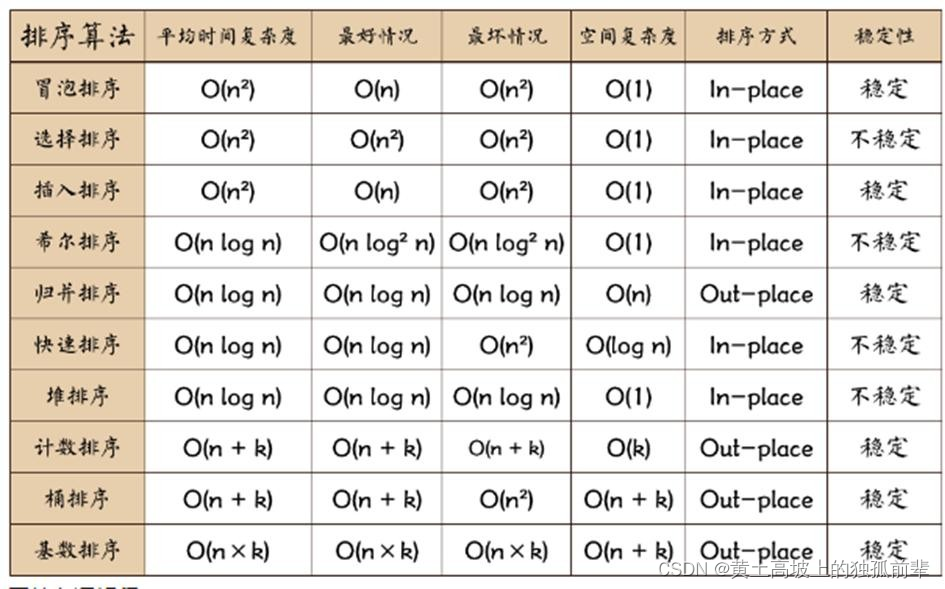
7.12.2 相关术语解释:
-
稳定:如果 a 原本在 b 前面,而 a=b,排序之后 a 仍然在 b 的前面;
-
不稳定:如果 a 原本在 b 的前面,而 a=b,排序之后 a 可能会出现在 b 的后面;
-
内排序:所有排序操作都在内存中完成;
-
外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
-
时间复杂度: 一个算法执行所耗费的时间。
-
空间复杂度:运行完一个程序所需内存的大小。
-
n: 数据规模
-
k: “桶”的个数
-
In-place: 不占用额外内存
-
Out-place: 占用额外内存
相关文章:

第 7 章 排序算法
文章目录 7.1 排序算法的介绍7.3 算法的时间复杂度7.3.1 度量一个程序(算法)执行时间的两种方法7.3.2 时间频度7.3.3 时间复杂度7.3.4 常见的时间复杂度7.3.5 平均时间复杂度和最坏时间复杂度 7.4 算法的空间复杂度简介7.4.1 基本介绍 7.5 冒泡排序7.5.1 基本介绍7.5.2 演示冒泡…...

机器人持续学习基准LIBERO系列7——计算并可视化点云
0.前置 机器人持续学习基准LIBERO系列1——基本介绍与安装测试机器人持续学习基准LIBERO系列2——路径与基准基本信息机器人持续学习基准LIBERO系列3——相机画面可视化及单步移动更新机器人持续学习基准LIBERO系列4——robosuite最基本demo机器人持续学习基准LIBERO系列5——…...

基于 Level set 方法的医学图像分割
摘 要 医学图像分割是计算机辅助诊断系统设计中的关键技术。对于医学图像分割问题,它一般可分为两部分:(l)图像中特定目标区域(器官或组织)的识别;(2)目标区域完整性的描述与提取。相比于其他图像,医学图像的复杂性和多样性,使得传统的基于底层图像信息的分割方法很难取得好的…...
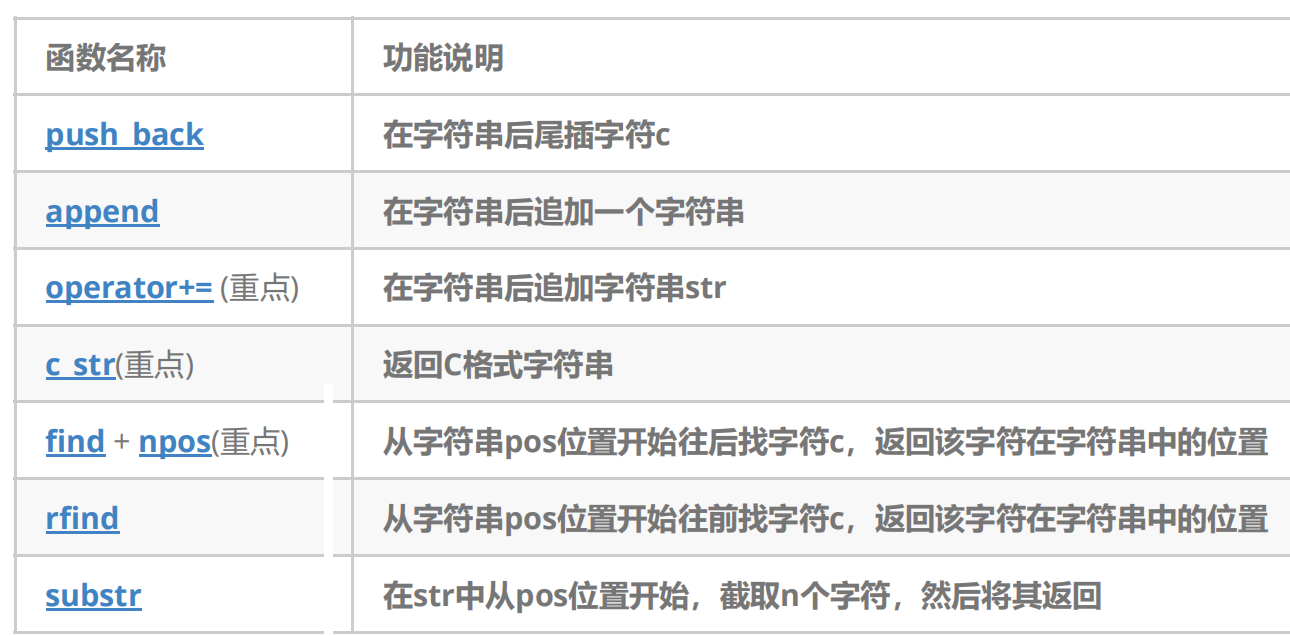
【C++入门】C++ STL中string常用函数用法总结
目录 前言 1. string使用 2. string的常见构造 3. string类对象的访问及遍历 迭代器遍历: 访问: 4. string类对象的容量操作 4.1 size和length 4.2 clear、empty和capacity 4.3 reserve和resize reserve resize 5. string类对象的修改操作 push_back o…...

Rust变量、常量声明与基本数据类型
Rust是一门系统级别的编程语言,注重安全性、性能和并发。在这篇博客中,我们将介绍Rust中的变量、常量声明以及基本数据类型,并通过示例说明每一种类型的用法。 变量声明 在Rust中,使用 let 关键字声明变量。变量默认是不可变的&…...
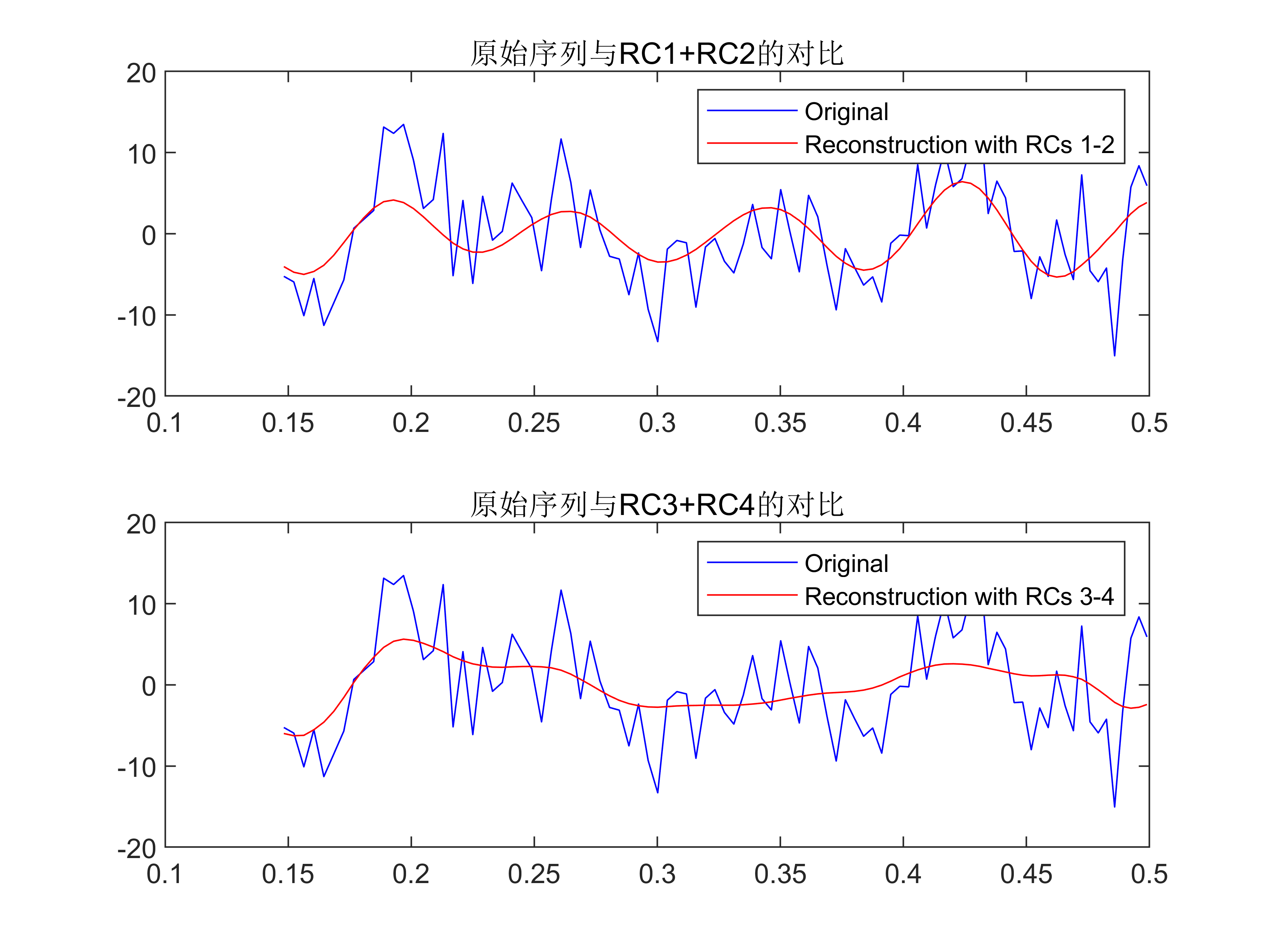
【MATLAB】 SSA奇异谱分析信号分解算法
有意向获取代码,请转文末观看代码获取方式~ 1 基本定义 SSA奇异谱分析(Singular Spectrum Analysis)是一种处理非线性时间序列数据的方法,可以对时间序列进行分析和预测。 它基于构造在时间序列上的特定矩阵的奇异值分解&#…...

Nginx+Tomcat负载均衡、动静分离以及Nginx负载均衡和四层代理
目录 NginxTomcat负载均衡、动静分离 Nginx 负载均衡模式: Nginx 四层代理配置: NginxTomcat负载均衡、动静分离 Nginx 服务器:192.168.80.10:80 Tomcat服务器1:192.168.80.100:80 Tomcat服务器2:192.168.80.101:80…...

Vue3中provide,inject使用
一,provide,inject使用: 应用场景:向孙组件传数据 应用Vue3碎片: ref,reactive,isRef,provide, inject 1.provide,inject使用 a.爷组件引入 import {ref,provide} from vue const drinkListre…...

Django命令模块
这篇文章我们主要来介绍一下关于 Django 的命令模块,我们经常会使用到,比如以下几个常用的命令,都属于 Django 的命令模块: python manage.py makemigrations python manage.py migrate python manage.py startapp python manage…...
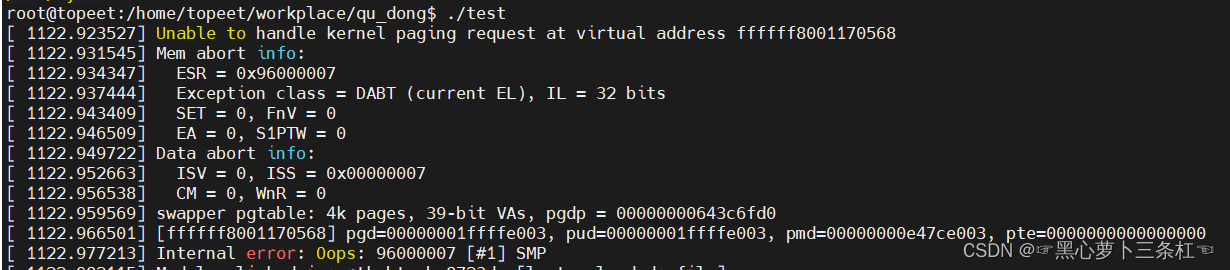
【linux驱动开发】在linux内核中注册一个杂项设备与字符设备以及内核传参的详细教程
文章目录 注册杂项设备驱动模块传参注册字符设备 开发环境: windows ubuntu18.04 迅为rk3568开发板 注册杂项设备 相较于字符设备,杂项设备有以下两个优点: 节省主设备号:杂项设备的主设备号固定为 10,在系统中注册多个 misc 设备驱动时&…...
)
Golang条件编译 | 获取系统的磁盘空间内存占用demo | gopsutil/disk库(跨平台方案)
文章目录 一、Golang条件编译1. 构建标签( Build tags)2. 文件后缀(File suffixes) 二、GO golang 获取磁盘空间 条件编译思路 三、【推荐】使用github.com/shirou/gopsutil/disk这个库,如何获取机器下不同磁盘分区的内容 一、Golang条件编译…...

22/76-池化
池化(最大池化层:选每个kernel中最大的数) 填充、步幅、多个通道: 池化层与卷积层类似,都具有填充和步幅。 没有可学习的参数。 在每个输入通道应用池化层以获得相应的输出通道。 输出通道数输入通道数。 平均池化层…...
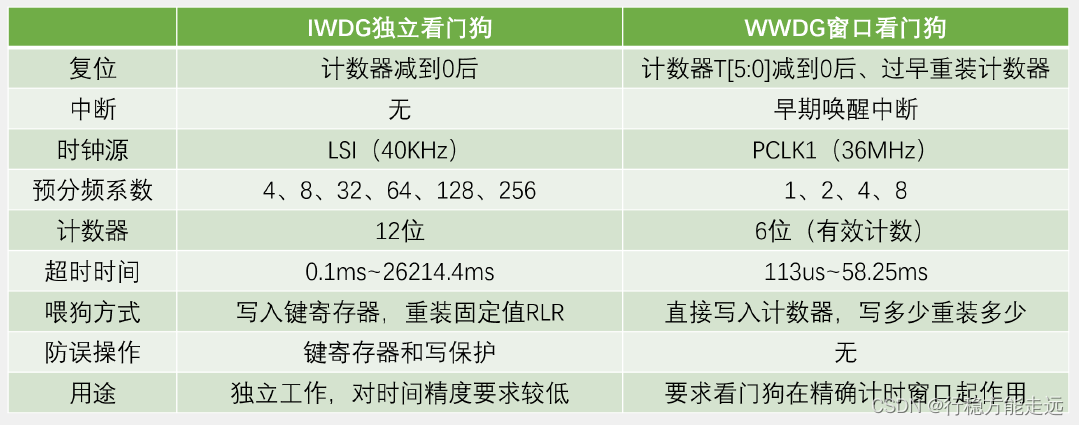
江科大STM32 下
目录 ADC数模转换器DMA直接存储器存取USART串口9-2 串口发送接受9-3 串口收发HEX数据包 I2C(mpu6050陀螺仪和加速度计)SPI协议10.1 SPI简介W25Q64简介10.3 SPI软件读写W25Q6410.4 SPI硬件读写W25Q64 BKP、RTC11.0 Unix时间戳11.1 读写备份寄存器BKP11.2 RTC实时时钟 十二、PWR1…...
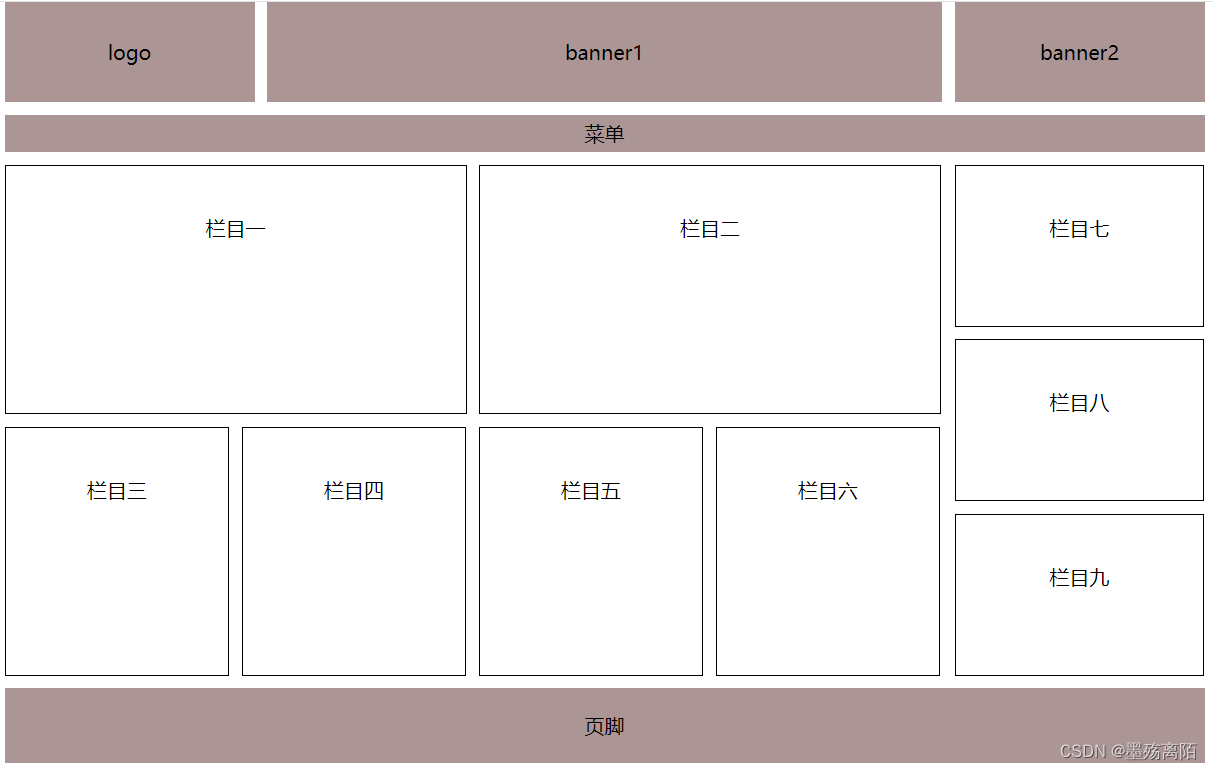
利用HTML和CSS实现的浮动布局
代码如下 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><style>*{m…...

2024年第十届控制、自动化与机器人国际会议(ICCAR 2024)即将召开!
2024年4月27~29日 新加披 会议官网:10th-ICCAR 2024https://iccar.org/index.html 第十届控制、自动化和机器人国际会议将于2024年4月27-29日在新加坡举办。本次会议由新加坡电子学会,IEEE机器人和自动控制协会和IEEE联合主办,并得到北京航空…...
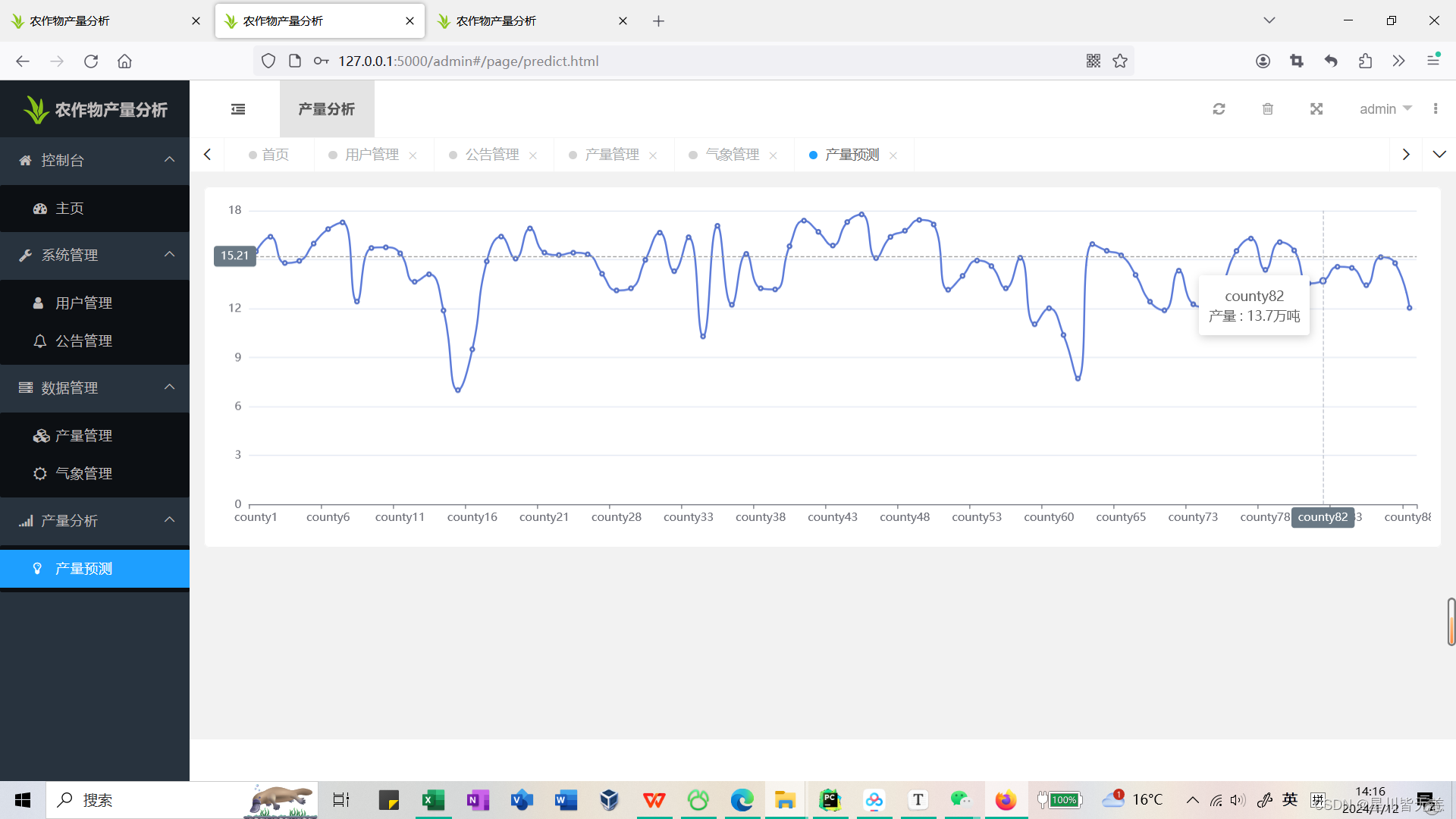
基于python集成学习算法XGBoost农业数据可视化分析预测系统
文章目录 基于python集成学习算法XGBoost农业数据可视化分析预测系统一、项目简介二、开发环境三、项目技术四、功能结构五、功能实现模型构建封装类用于网格调参训练模型系统可视化数据请求接口模型评分 0.5*mse 六、系统实现七、总结 基于python集成学习算法XGBoost农业数据可…...
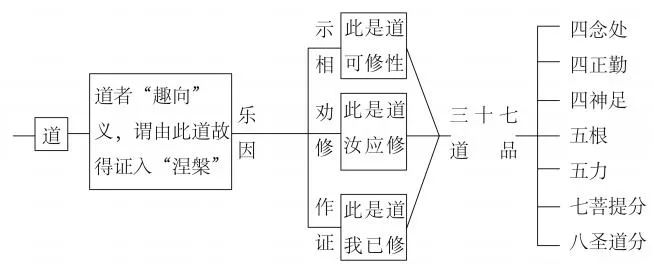
第29集《佛法修学概要》
丁三、声闻乘 分二:戊一、释义;戊二、四谛法;戊三、结示 请大家打开讲义第八十二页。我们看丁三,声闻乘。 在祖师大德的判教当中,把我们整个大乘的成佛之道分成了三个部分:第一个是安乐道,第…...

奥伦德光电耦合器5G通信领域及其相关领域推荐
光电耦合器是以光为媒介传输电信号的一种电-光-电转换器件。由于该器件使用寿命长、工作温度范围宽,所以在过程控制、工业通信、家用电器、医疗设备、通信设备、计算机以及精密仪器等方面有着广泛应用在当前工艺技术持续发展与提升的过程中,其工作速度、…...

机器学习算法 - 马尔可夫链
马尔可夫链(Markov Chain)可以说是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测、语音识别方面都有着极其广泛的应用 > The future is independent of the past given the present 未来独立于过去ÿ…...

Linux下防火墙相关命令整理
目录 一.前言二.相关命令整理 一.前言 这篇文章简单整理一下Linux系统中防火墙相关命令。 二.相关命令整理 开启防火墙 systemctl start firewalld关闭防火墙 systemctl stop firewalld重启防火墙 systemctl restart firewalld开机启用防火墙 systemctl enable firewall…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
