【论文阅读】Consistency Models
文章目录
- Introduction
- Diffusion Models
- Consistency Models
- Definition
- Parameterization
- Sampling
- Training Consistency Models via Distillation
- Training Consistency Models in Isolation
- Experiment
Introduction
-
相比于单步生成的模型(例如
GANs, VAEs, normalizing flows),扩散模型的迭代式生成过程需要 10 到 2000 步计算来采样,导致推理速度低,实时性应用受限. -
本文的目的是创造高效、单步的生成,同时不牺牲迭代采样的优势。在数据到噪声的 PF-ODE 轨迹上,学习轨迹上任意点到轨迹起点的映射,对这些映射的建模成为 consistency model.

-
两种训练 consistency model的方法
- 使用 numerical ODE solver 和预训练的扩散模型在 PF-ODE 轨迹上生成若干相邻点对,通过最小化模型输出点对间的距离(相似度),蒸馏出
consistency model. - 不依赖预训练扩散模型,独立训练一个
consistency model.
- 使用 numerical ODE solver 和预训练的扩散模型在 PF-ODE 轨迹上生成若干相邻点对,通过最小化模型输出点对间的距离(相似度),蒸馏出
-
在一些数据集上测试.
Diffusion Models
使用 p d a t a ( x ) p_{data}(\mathrm{x}) pdata(x)表示数据分布,扩散模型使用如下随机微分公式对服从原分布的数据进行扩散:
d x t = μ ( , x t , t ) + σ ( t ) d w t \large \mathrm{dx}_t = \mu(\mathrm,{x}_t, t) + \sigma(t)\mathrm{dw}_t dxt=μ(,xt,t)+σ(t)dwt
其中 t t t为时间步,范围是 0 0 0 到 T T T, μ ( ⋅ , ⋅ ) \mu(·,·) μ(⋅,⋅) 和 σ ( ⋅ ) \sigma(·) σ(⋅)分别是布朗运动中的漂移系数和扩散系数, x t \mathbf{x}_t xt服从分布 p t ( x ) p_{t}(\mathrm{x}) pt(x), x 0 \mathrm{x}_0 x0服从分布 p d a t a ( x ) p_{data}(\mathrm{x}) pdata(x). 该方程的一个重要属性是,其存在一个 PF-ODE 方程:
d x t = [ μ ( x t , t ) − 1 2 σ ( t ) 2 ∇ log p t ( x t ) ] d t \large\mathrm{dx}_t = \left[ \mu(\mathrm{x}_t, t)-\frac{1}{2}\sigma(t)^2 \nabla\log{p_t(\mathrm{x}_t)} \right]\mathrm{d}t dxt=[μ(xt,t)−21σ(t)2∇logpt(xt)]dt
其中 ∇ log p t ( x ) \nabla\log{p_t(\mathrm{x})} ∇logpt(x)是 p t ( x ) p_t(\mathrm{x}) pt(x)的 score function.
在 SDE 中,令漂移系数 μ ( x , t ) = 0 \mu(\mathrm{x}, t) = 0 μ(x,t)=0, 扩散系数 σ ( t ) = 2 t \sigma(t) = \sqrt{2t} σ(t)=2t. 使用得分匹配的方式训练模型 s ϕ ( x , t ) ≈ ∇ log p t ( x ) s_{\phi}(\mathrm{x},t) \approx \nabla\log{p_t(\mathrm{x})} sϕ(x,t)≈∇logpt(x),代入 PF-ODE 方程,得到 empirical PF-ODE:
d x t d t = − t s ϕ ( x t , t ) \large \frac{\mathrm{dx}_t}{\mathrm{d}t}=-ts_{\phi}(\mathrm{x}_t,t) dtdxt=−tsϕ(xt,t)
采样时,使用 x ^ T ∼ N ( 0 , T 2 I ) \hat{\mathrm{x}}_T\sim\mathcal{N}(0, T^2I) x^T∼N(0,T2I)初始化,再使用 numerical ODE solver(例如 Euler, Heun)按时间步倒推出 x ^ 0 \hat{x}_0 x^0. 为了防止数值不稳定,会在 t = ϵ t=\epsilon t=ϵ是提前终止, ϵ \epsilon ϵ为一个正小数,同时将 x ^ ϵ \hat{\mathrm{x}}_{\epsilon} x^ϵ作为结果.
扩散模型的瓶颈在于采样速度慢, ODE solver 利用得分模型 s ϕ ( x , t ) s_{\phi}(\mathrm{x},t) sϕ(x,t)迭代求解,消耗算力多. 目前存在一些更快的 ODE solver,但是仍然需要大于 10 10 10 步的采样. 也存在一些蒸馏方法,但是大多数方法需要从扩散模型中采集巨大的数据集,同样消耗算力多.
Consistency Models
Definition
根据 PF-ODE 得到一条解路径 { x t } t ∈ [ ϵ , T ] \{\mathrm{x}_t\}_{t\in[\epsilon, T]} {xt}t∈[ϵ,T],将 consistency function 定义为:
f : ( x t , t ) ↦ x ϵ \large f:(\mathrm{x}_t, t) \mapsto \mathrm{x}_{\epsilon} f:(xt,t)↦xϵ
对于该路径上的任意点 ( x t , t ) (\mathrm{x}_t, t) (xt,t),其输出是一致的. 对于任意的 t , t ′ ∈ [ ϵ , T ] t, t' \in [\epsilon, T] t,t′∈[ϵ,T],有 f ( x t , t ) = f ( x t ′ , t ′ ) f(\mathrm{x}_t, t) =f(\mathrm{x}_{t'}, t') f(xt,t)=f(xt′,t′)恒成立.

Parameterization
令 F θ ( x , t ) F_{\theta}(\mathrm{x}, t) Fθ(x,t)表示任意形式的神经网络,使用 sikp connection 可以将模型表示为:
f θ ( x , t ) = c s k i p ( t ) x + c o u t ( t ) F θ ( x , t ) \large f_{\theta}(\mathrm{x}, t)=c_{skip}(t)\mathrm{x}+c_{out}(t)F_{\theta}(\mathrm{x},t) fθ(x,t)=cskip(t)x+cout(t)Fθ(x,t)
其中边界条件为 c s k i p ( ϵ ) = 1 c_{skip}(\epsilon)=1 cskip(ϵ)=1, c o u t ( ϵ ) = 0 c_{out}(\epsilon)=0 cout(ϵ)=0.
具体为:
c s k i p ( t ) = σ d a t a 2 ( t − ϵ ) 2 + σ d a t a 2 \large c_{skip}(t)=\frac{\sigma_{data}^2}{(t-\epsilon)^2+\sigma_{data}^2} cskip(t)=(t−ϵ)2+σdata2σdata2
c o u t ( t ) = σ d a t a ( t − ϵ ) σ d a t a 2 + t 2 \large c_{out}(t)=\frac{\sigma_{data}(t-\epsilon)}{\sqrt{\sigma_{data}^2+t^2}} cout(t)=σdata2+t2σdata(t−ϵ)
σ d a t a \sigma_{data} σdata取值 0.5 0.5 0.5.
Sampling
有了一个训练好的 consistency model f θ ( ⋅ , ⋅ ) f_{\theta}(·, ·) fθ(⋅,⋅)之后,从高斯噪声 N ( 0 , T 2 I ) \mathcal{N}(0, T^2I) N(0,T2I)采样 x ^ T \hat{\mathrm{x}}_T x^T,再代入模型一步推出 x ^ ϵ = f θ ( x T ^ , T ) \hat{\mathrm{x}}_{\epsilon}=f_{\theta}(\hat{\mathrm{x}_T}, T) x^ϵ=fθ(xT^,T).为了提高质量,也可以进行多步采样,算法如下:

Training Consistency Models via Distillation
作者的第一个方法是在预训练的得分模型 s ϕ ( x , t ) s_{\phi}(\mathrm{x},t) sϕ(x,t)上蒸馏.
首先考虑将 ϵ \epsilon ϵ到 T T T的时间离散化成 N − 1 N-1 N−1 个间隔,也即 t 1 = ϵ < t 2 < t 3 < . . . < t N = T t_1=\epsilon<t_2<t_3<...<t_N=T t1=ϵ<t2<t3<...<tN=T. 在实践中,使用如下公式:
t i = ( ϵ 1 / ρ + i − 1 N − 1 ( T 1 / ρ − ϵ 1 / ρ ) ) ρ \large t_i=\left(\epsilon^{1/\rho} + \frac{i-1}{N-1}\left(T^{1/\rho}-\epsilon^{1/\rho}\right) \right)^{\rho} ti=(ϵ1/ρ+N−1i−1(T1/ρ−ϵ1/ρ))ρ
其中 ρ = 7 \rho=7 ρ=7. 当 N N N充分大时,可以获得 x t n \mathrm{x}_{t_n} xtn到 x t n + 1 \mathrm{x}_{t_{n+1}} xtn+1的准确估计,于是 x ^ t n ϕ \hat{\mathrm{x}}_{t_n}^{\phi} x^tnϕ可以定义为:
x ^ t n ϕ = x t n + 1 + ( t n − t n + 1 ) Φ ( x t n + 1 , t n + 1 ; ϕ ) \large \hat{\mathrm{x}}_{t_n}^{\phi}=\mathrm{x}_{t_{n+1}} + (t_n-t_{n+1})\Phi(\mathrm{x}_{t_{n+1}}, t_{n+1};\phi) x^tnϕ=xtn+1+(tn−tn+1)Φ(xtn+1,tn+1;ϕ)
Φ ( . . . ; ϕ ) \Phi(...;\phi) Φ(...;ϕ)为 one-step ODE solver(比如Euler).
从数据集中采样 x \mathrm{x} x,通过 SDE 加噪 N ( x , t n + 1 2 I ) \mathcal{N}(\mathrm{x}, t_{n+1}^2I) N(x,tn+12I)得到 x t n + 1 \mathrm{x}_{t_{n+1}} xtn+1, 然后使用 ODE solver 求解出 x ^ t n ϕ \hat{\mathrm{x}}_{t_n}^{\phi} x^tnϕ,通过最小化在 x ^ t n ϕ \hat{\mathrm{x}}_{t_n}^{\phi} x^tnϕ 和 x t n + 1 \mathrm{x}_{t_{n+1}} xtn+1计算结果的差距训练模型.
Definition 1
consistency distillation loss (CD)表示为:
L C D N ( θ , θ − ; ϕ ) = E [ λ ( t n ) d ( f θ ( x t n + 1 , t n + 1 ) , f θ − ( x ^ t n ϕ , t n ) ] \large \mathcal{L}_{CD}^{N}(\theta, \theta^-;\phi)=\mathbb{E}\left[\lambda(t_n)d(f_{\theta}(\mathrm{x}_{t_{n+1}},t_{n+1}),f_{\theta^-}(\hat{\mathrm{x}}_{t_n}^{\phi}, t_n) \right] LCDN(θ,θ−;ϕ)=E[λ(tn)d(fθ(xtn+1,tn+1),fθ−(x^tnϕ,tn)]
其中, λ ( ⋅ ) ∈ R + \lambda(·)\in\mathbb{R}^+ λ(⋅)∈R+是正权重函数, θ − \theta^- θ−是 θ \theta θ在优化过程中历史值的均值. d ( ⋅ , ⋅ ) d(·,·) d(⋅,⋅)是一个度量函数,满足当且仅当两个输入相等时为 0 0 0,其余情况大于 0 0 0.
作者考虑 d ( ⋅ , ⋅ ) d(·,·) d(⋅,⋅) 使用 l 1 l_1 l1 以及 l 2 l_2 l2,在实验中 λ ( t n ) ≡ 1 \lambda(t_n) \equiv1 λ(tn)≡1表现较好. θ − \theta^- θ−使用 EMA 更新,计算公式如下:
θ − ← s t o p g a r d ( μ θ − + ( 1 − μ ) θ ) \large \theta^- \leftarrow \mathrm{stopgard}(\mu\theta^-+(1-\mu)\theta) θ−←stopgard(μθ−+(1−μ)θ)
其中 0 ≤ μ < 1 0\le\mu<1 0≤μ<1. 使用 EMA 可以使训练更稳定,同时能提高模型的表现.
模型训练算法如下:

Training Consistency Models in Isolation
consistency model 可以不依赖预训练扩散模型训练,使用如下无偏估计替换 ∇ log p t ( x ) \nabla\log{p_t(\mathrm{x})} ∇logpt(x):
∇ log p t ( x ) = − E [ x t − x t 2 ∣ x t ] \large \nabla\log{p_t(\mathrm{x})}=-\mathbb{E}\left[\left.\frac{\mathrm{x}_t-\mathrm{x}}{t^2}\right|\mathrm{x}_t \right] ∇logpt(x)=−E[t2xt−x xt]
consistency training loss (CT)表示为:
L C D N ( θ , θ − ) = E [ λ ( t n ) d ( f θ ( x + t n + 1 z , t n + 1 ) , f θ − ( x + t n z , t n ) ] \large \mathcal{L}_{CD}^{N}(\theta, \theta^-)=\mathbb{E}\left[\lambda(t_n)d(f_{\theta}(\mathrm{x}+t_{n+1}\mathrm{z},t_{n+1}),f_{\theta^-}(\mathrm{x}+t_{n}\mathrm{z},t_{n}) \right] LCDN(θ,θ−)=E[λ(tn)d(fθ(x+tn+1z,tn+1),fθ−(x+tnz,tn)]
其中 z ∼ N ( 0 , I ) \mathrm{z}\sim\mathcal{N}(0,I) z∼N(0,I). 损失函数的计算依赖于 f θ f_{\theta} fθ和 f θ − f_{\theta^-} fθ−,且与扩散模型的无关.
为了提升模型效果,使用 schedule function N ( ⋅ ) N(·) N(⋅)控制 N N N 增长. 直觉上,当 N N N 小的时候,使用 consistency distillation loss 模型在一开始收敛更快,同时方差小、偏差大. 反之,在训练结束时,应当使 N N N 大,这样方差大、偏差小。同时,使用 schedule function μ ( ⋅ ) \mu(·) μ(⋅)替换 μ \mu μ,让它随着 N N N 增长而变化.
N ( ⋅ ) N(·) N(⋅)和 μ ( ⋅ ) \mu(·) μ(⋅)具体为
N ( k ) = ⌈ k K ( ( s 1 + 1 ) 2 − s 0 2 ) + s 0 2 − 1 ⌉ + 1 \large N(k)= \left\lceil\sqrt{\frac{k}{K}((s_1+1)^2-s_0^2)+s_0^2}-1 \right\rceil+1 N(k)= Kk((s1+1)2−s02)+s02−1 +1
μ ( k ) = exp ( s 0 log μ 0 N ( k ) ) \large \mu(k)=\exp\left(\frac{s_0\log{\mu_0}}{N(k)}\right) μ(k)=exp(N(k)s0logμ0)
K K K表示整体训练步数, s 0 s_0 s0表示开始的离散化步数.
训练算法如下:

Experiment
关于 CD ,作者分别使用 l 1 l_1 l1, l 2 l_2 l2, L P I P S \mathrm{LPIPS} LPIPS作为度量函数,使用一阶Euler和二阶Heun座位 ODE solver, N N N取 { 9 , 12 , 18 , 36 , 50 , 60 , 80 , 120 } \{9,12,18,36,50,60,80,120\} {9,12,18,36,50,60,80,120},使用相应的预训练扩散模型做初始化. 使用 CT 训练的模型则随机初始化.

(a) 对比不同的度量函数在 CD 上的表现,其中 LPIPS 的效果最好.
(b, c) 对不不同 ODE solver 和 N N N在 CD 上的表现,使用 Heun 且 N N N取 18 18 18时效果最好.在取相同的 N N N时,二阶Heun的表现优于一阶Euler,因为高阶的 ODE solver 的估计误差更小. 当 N N N充分大时,模型对 N N N变得不敏感.
(d) 根据之前的结论,关于 CT 的实验使用 LPIPS 作为度量函数. 更小的 N N N收敛更快,但是采样结构更差;使用自适应的 N ( ⋅ ) N(·) N(⋅)和 μ ( ⋅ ) \mu(·) μ(⋅)效果最好.
对比 CD 和 progressive disillation(PD) 在不同数据集上的效果,CD 的表现普遍比 PD 好.

对比 CT 和其它生成模型,仅使用一步或两步生成.

Zero-Shot Image Editing

相关文章:

【论文阅读】Consistency Models
文章目录 IntroductionDiffusion ModelsConsistency ModelsDefinitionParameterizationSampling Training Consistency Models via DistillationTraining Consistency Models in IsolationExperiment Introduction 相比于单步生成的模型(例如 GANs, VAEs, normalizi…...
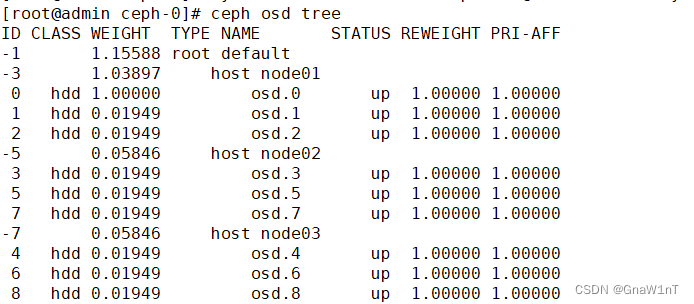
Ceph应用管理
目录 资源池 Pool 管理 创建 CephFS 文件系统 MDS 接口 服务端操作 客户端操作 创建 Ceph 块存储系统 RBD 接口 创建 Ceph 对象存储系统 RGW 接口 OSD 故障模拟与恢复 资源池 Pool 管理 我们如何向 Ceph 中存储数据呢?首先我们需要在 Ceph 中定义一个 Pool…...

大师学SwiftUI第6章 - 声明式用户界面 Part 3
安全域视图 SwiftUI还内置了创建安全文本框的视图。这一视图会把用户输入的字符替换成点以及隐藏敏感信息,比如密码。 SecureField(String, text: Binding):该初始化方法创建一个安全输入框。第一个参数定义占位文本,text参数为存储…...

使用AI自动生成PPT提高制作效率
使用AI自动生成PPT提高制作效率 在制作PPT方面,很多制作者都会轻易跳进一个怪圈:“我要制作一个关于关爱老人的PPT,该怎么做呢,有模板没有?”这个会涉及很多逻辑需要经过不断的思考,制作PPT要通过很多素材、使用技巧、…...

Servlet中访问网页常遇到的问题
网页出现404 出现这一种情况是浏览器访问的资源不存在 第一种情况通常是路径出错请检查你的路径是否一致 第二种情况确认你的webapp是否被正确加载 smart tomcat由于只加载一个webapp 如果加载失败 就会直接启动失败 拷贝war方式到Tomcat要加载多个webapp如果失败只有日志 查…...
Vue加载序列帧动图
解读方法 使用<img :src"currentFrame" alt"加载中" /> 加载图片动态更改src的值使用 requestAnimationFrame 定时更新在需要的页面调用封装的组件 <LoadToast v-if"showLoading" /> 封装组件 <template><div class"…...

k8s的配置资源管理
1、configmap*:1.2加入新的特征(重点) 2、secret:保存密码,token,保存敏感的k8s资源(保存加密的信息) (1)敏感的k8s资源,这类数据可以直接存放在…...
vue 指定区域可拖拽的限定拖拽区域的div(如仅弹窗标题可拖拽的弹窗)
<template><div class"container" ref"container"><div class"drag-box" v-drag><div class"win_head">弹窗标题</div><div class"win_content">弹窗内容</div></div><…...
【idea】idea插件编写教程,博主原创idea插件已上架idea插件市场 欢迎下载
前言:经常使用Objects.equals(a,b)方法的同学 应该或多或少都会因为粗心而传错参, 例如日常开发中 我们使用Objects.equals去比较 status(入参),statusEnum(枚举), 很容易忘记statusEnum.getCode() 或 statusEnum.getVaule() ,再比…...

探索Python数据结构与算法:解锁编程的无限可能
文章目录 一、引言1.1 数据结构与算法对于编程的重要性1.2 Python作为实现数据结构与算法的强大工具 二、列表和元组2.1 列表:创建列表、索引、切片和常用操作2.2 元组:不可变序列的特性和使用场景 三、字符串操作和正则表达式3.1 字符串的常见操作和方法…...

责任链模式介绍及演示
责任链模介绍 责任链模式(Chain of Responsibility Pattern)是一种行为设计模式,其主要目的是将请求的发送者和接收者解耦。在这个模式中,多个对象有机会处理一个请求,形成一条“责任链”。每个对象在链中检查该请求并…...
表单组件属性说明+代码明细)
智能小程序小部件(Widget)表单组件属性说明+代码明细
在 Tuya MiniApp Tools 中,新建项目并选择小部件(Widget)对应模板即可自动创建小部件(Widget)项目。 button 按钮,用于强调操作并引导用户去点击。 属性说明 属性名类型默认值必填说明sizestringdefault否按钮的大小typestringdefault否按钮的样式类…...

自学Python笔记总结(更新中……)
自学Python笔记总结 网址数据类型类型查看类型,使用type内置类标识符 输出输入语句format函数的语法及用法数据类型的转换运算符算数运算符赋值运算符的特殊场景拆包 比较运算符逻辑运算符 与 短路位运算符运算符优先级 程序流程控制分支语句pass 占位 循环语句 whi…...

十四.变量、异常处理
变量、异常处理 1.变量1.1系统变量1.1.1系统变量分类1.1.2查看系统变量 1.2用户变量1.2.1用户变量分类1.2.2会话用户变量1.2.3局部变量1.2.4对比会话用户变量与局部变量 补充:MySQL 8.0的新特性—全局变量的持久化 2.定义条件与处理程序2.1案例分析2.2定义条件2.3定义处理程序2…...
import { ArrowRight } from “@element-plus/icons-vue“;
今天下午快被这个问题折磨疯了 虽然知道这个问题怎么产生的 但项目里那个碍眼的红线就是去不掉 后来才发现 这是插件的锅 我的心情 你知道我想要说什么的 想必能看到这篇文章的 也知道这个问题是怎么产生的 vue3ts使用的时候 默认是需要带上文件名的 但是引入el组件时 …...

Kubernetes 面试宝典
创建 Pod的主要流程? 客户端提交 Pod 的配置信息(可以是 yaml 文件定义的信息)到 kube-apiserver. Apiserver 收到指令后,通知 controllr-manager 创建一个资源对象 controller-manager 通过 apiserver 将 pod 的配置信息存储到 ETCD 数据中薪心中 kube-scheduler 检查到 p…...

c语言二维数组
系列文章目录 c语言二维数组 c语言二维数组 系列文章目录一、二维数组的定义一、二维数组的内存模型 一、二维数组的定义 int main() {//二维数组的定义int arr[3][4];arr[0][0]; arr[0][1]; arr[0][2]; arr[0][3]; arr[0][4];arr[1][0]; arr[1][1]; arr[1][2]; arr[1][3]; ar…...
ArcGIS Pro 拓扑编辑和常见一些拓扑错误处理
7.4 拓扑编辑 拓扑编辑也叫共享编辑,多个数据修改时,一块修改,如使用数据:chp7\拓扑检查.gdb,数据集DS下JZX、JZD和DK,加载地图框中,在“地图”选项卡下选择“地图拓扑”或“ds_Topology(地理数据库)”&…...
前端踩坑之——antDesignVue的upload组件
本地启动时控制台会报404,放到服务器上控制台会报405(多发一个请求) 原因:upLoad有默认的上传事件 解决:阻止默认事件即可 beforeUpload Hook function which will be executed before uploading. Uploading will be stopped with false or …...

设计模式——策略模式
策略模式(Strategy Pattern)是一种行为型设计模式,它定义了一系列算法,并将每一个算法封装起来,使它们可以相互替换。策略模式让算法独立于使用它的客户端代码,使得算法的变化不会影响到使用该算法的客户端…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
