异步Merkle Tree
1. 引言
前序博客:
- 利用多核的Rust快速Merkle tree
Anoushk Kharangate 2023年论文《Asynchronous Merkle Trees》,其对Merkle tree数据结构进行修改,使得可跨多线程异步计算。
开源代码实现见:
- https://github.com/anoushk1234/async-merkle-tree(Rust)
Merkle tree应用广泛,有各种变种,如:
- Jellyfish Merkle Tree
- Sparse Merkle Tree
但这些都存在一个共同的问题:
- 当用Merkle Tree来处理大数据集时,计算该tree的开销,将大幅增加。此外,插入单个叶子节点,将需要重构整棵树。
在某些情况下,插入叶子节点时的计算时间,应尽可能短,且对于数据并行处理的场景,需要能异步计算。《Asynchronous Merkle Trees》论文中:
- 提出了并行处理一组数据,批量异步所构建的Merkle Tree,在每次插入时,无需重新计算该tree。
2. Asynchronous Merkle Trees(AMT)
Asynchronous Merkle Trees(AMT)有如下关键属性:
- 1)节点类型:包含3种特殊节点:
- 1.1)Digest节点:仅简单用作另一batch node的placeholder。
- 1.2)Layer Checkpoint(LC)节点
- 1.3)Compound节点:
- 2个LC节点组成一个Compound节点。
- 一个LC节点和一个Compound节点,组成另一Compound节点。
- 2)排序:每个特殊节点必须包含一个order bit,以表示是其父节点的左子节点,还是右子节点。
- 3)Segregation隔离:每个节点必须有一个batch bit,以表示其属于哪个batch。
某Merkle Tree T T T,其遵循如下要求:
- 1) T T T的高度为 h h h,其中 h = log 2 ( n ) h=\log_2(n) h=log2(n), n n n为叶子节点数
- 2) T T T必须最多有 M M M个节点,其中 M = ∑ n h n 2 M=\sum_{n}^{h}\frac{n}{2} M=∑nh2n
- 3)叶子节点表示为 N i N_i Ni,其中 { i ∈ N ∣ 0 ≤ i ≤ 2 D } \{i\in N|0\leq i \leq 2^D\} {i∈N∣0≤i≤2D}
将以上Merkle Tree T T T,扩展为,创建AMT,其遵循如下要求:
- 1)异步附加的叶子称为Batches B B B,batches的数量和其叶子必须提取已知。
- 2)以大量Digest Nodes D i D_i Di来初始化该tree,Digest Nodes D i D_i Di用作其它batches节点的placeholder。

如上图所示,以3层Merkle tree为例,当附加红色batch叶子时,需重新计算 N 11 N_{11} N11和 N 12 N_{12} N12,无法异步附加。
对应的AMT为4层:


对应每个节点必须包含如下数据:
- 1)Batch:一个整数值,用于表示该节点属于哪个batch
- 对于Compound节点,可将其设置为(与现有batch id不冲突的)某特殊整数值,来表示该节点不属于特定batch。
- 2)Order:一个整数值,为0或1,以表示左节点或右节点。
- 3)Data:实际的数据哈希值。

Merkle tree系列博客
- 利用多核的Rust快速Merkle tree
- Merkle tree proof
- Merkle tree及其在区块链等领域的应用
- Sparse Merkle Tree
- 以太坊EIP-1186:RPC-Method to get Merkle Proofs - eth_getProof
- proof of solvency(偿付能力证明)方案
- 以太坊中的modified Merkle Patricia Trie
- 以太坊Eth2 deposit merkle tree
- Polygon zkEVM中的Merkle tree
- Merkle tree for non-membership proof
- Polygon zkEVM Merkle tree的circom约束
- Zcash中的merkle tree
相关文章:

异步Merkle Tree
1. 引言 前序博客: 利用多核的Rust快速Merkle tree Anoushk Kharangate 2023年论文《Asynchronous Merkle Trees》,其对Merkle tree数据结构进行修改,使得可跨多线程异步计算。 开源代码实现见: https://github.com/anoushk1…...

7. UE5 RPG修改GAS的Attribute的值
前面几节文章介绍了如何在角色身上添加AbilitySystemComponent和AttributeSet。并且还实现了给AttributeSet添加自定义属性。接下来,实现一下如何去修改角色身上的Attribute的值。 实现拾取药瓶回血功能 首先创建一个继承于Actor的c类,actor是可以放置到…...

Oracle/DM序列基本使用
序列(SEQUENCE)是序列号生成器,可以为表中的行自动生成序列号,产生一组等间隔的数值(类型为数字)。其主要的用途是生成表的主键值,可以在插入语句中引用,也可以通过查询检查当前值,或使序列增至下一个值。序列是一个计…...

校验ChatGPT 4真实性的三个经典问题:提供免费测试网站快速区分 GPT3.5 与 GPT4
现在已经有很多 ChatGPT 的套壳网站,以下分享验明 GPT-4 真身的三个经典问题,帮助你快速区分套壳网站背后到底用的是 GPT-3.5 还是 GPT-4。 大家可以在这个网站测试:https://ai.hxkj.vip,免登录可以问三条,登录之后无限…...
概率论与数理统计————3.随机变量及其分布
一、随机变量 设E是一个随机试验,S为样本空间,样本空间的任意样本点e可以通过特定的对应法则X,使得每个样本点都有与之对应的数对应,则称XX(e)为随机变量 二、分布函数 分布函数:设X为随机变量…...

掌握单例模式的极致挑战:能否默写饿汉式代码?
目录 1.前言 2.本质 3.代码默写 1.前言 在面试中,理解和掌握单例模式是非常重要的。本文旨在帮助读者深入理解饿汉式单例模式,并通过简洁明了的解释和示例代码,使读者能够轻松掌握并默写出饿汉式单例模式的代码实现。 2.本质 饿汉式单例模…...

力扣刷MySQL-第三弹(详细讲解)
🎉欢迎您来到我的MySQL基础复习专栏 ☆* o(≧▽≦)o *☆哈喽~我是小小恶斯法克🍹 ✨博客主页:小小恶斯法克的博客 🎈该系列文章专栏:力扣刷题讲解-MySQL 🍹文章作者技术和水平很有限,如果文中出…...
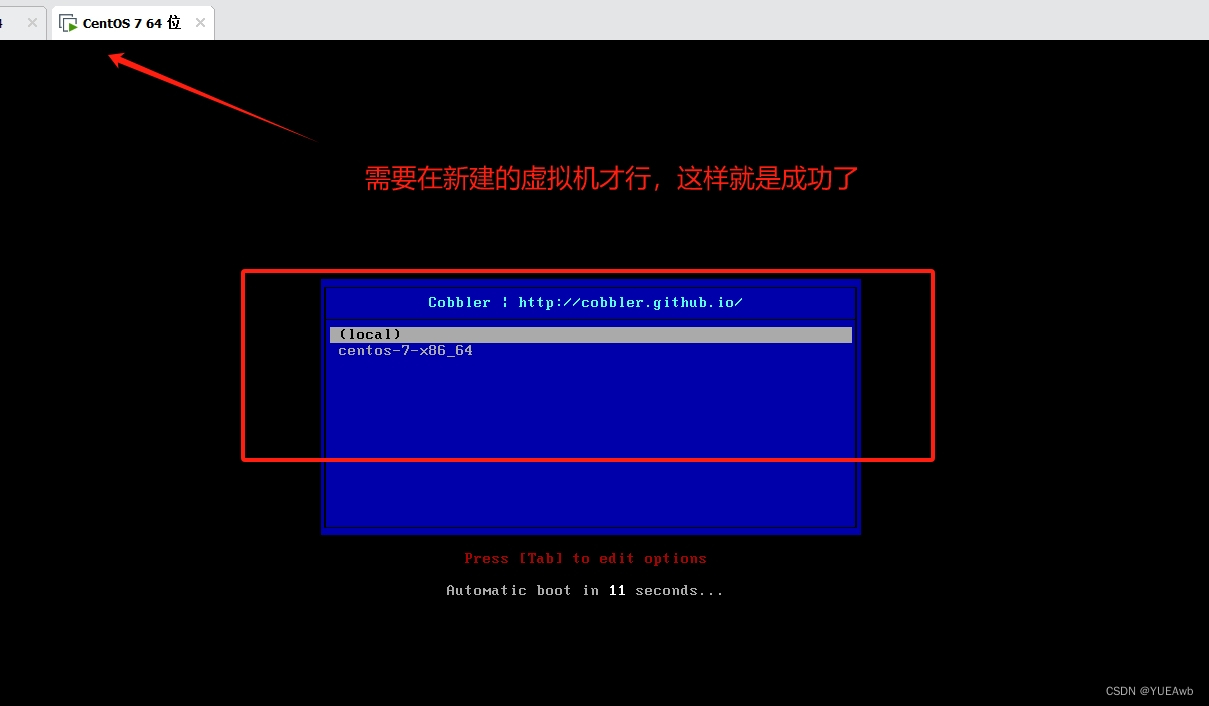
PXE和kickstart无人值守安装
PXE高效批量网络装机 引言 1.系统装机的引导方式 启动 操作 系统 1.硬盘 2.光驱(u盘) 3.网络启动 pxe 重装系统? 在已有操作系统 新到货了一台服务器, 装操作系统 系统镜像 u盘 光盘 pe: 小型的 操作系统 在操…...
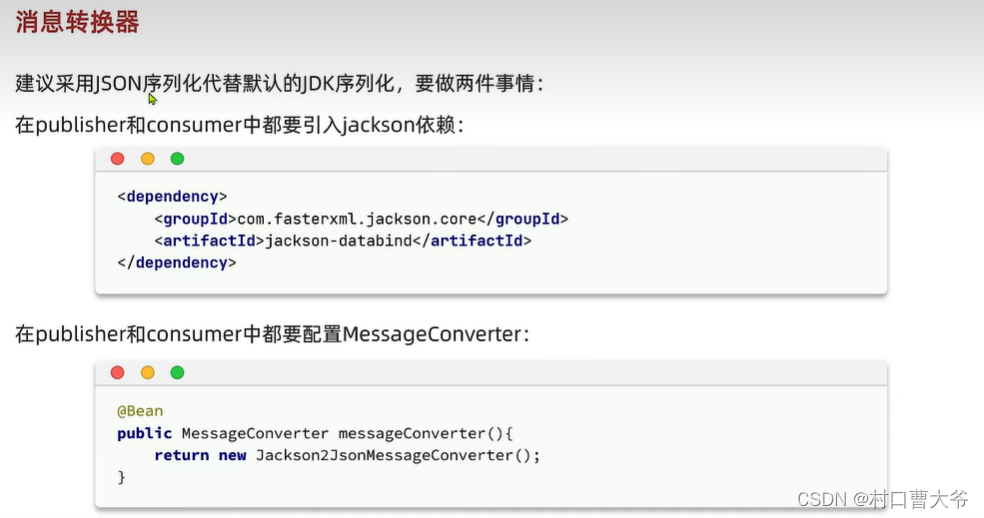
rabbitmq基础教程(ui,java,springamqp)
概述:安装看我上篇文章Docker安装rabbitmq-CSDN博客 任务一 创建一个队列 这样创建两个队列 在amq.fanout交换机里面发送数据 模拟发送数据 发送消息,发现一下信息: 所以得出理论,消息发送是先到交换机,然后由交换机…...

无重复字符的最长子串[中等]
优质博文:IT-BLOG-CN 一、题目 给定一个字符串s,请你找出其中不含有重复字符的最长子串的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是"abc",所以其长度为3。 示例 2: 输入: s &…...

考研经验总结——目录
文章目录 一、写作顺序二、个人情况说明三、读评论四、一些小牢骚五、一些注意事项(持续更新) 一、写作顺序 我将准备从三个阶段开始介绍吧 考研前考研中考研后(也就是现在我的这种情况) 考研前我会分为:数学、专业…...

Docker(一)简介和基本概念
一、简介 本章将带领你进入 Docker 的世界。 什么是 Docker? 用它会带来什么样的好处? 好吧,让我们带着问题开始这神奇之旅。 1.什么是 Docker Docker 最初是 dotCloud 公司创始人 Solomon Hykes 在法国期间发起的一个公司内部项目&…...
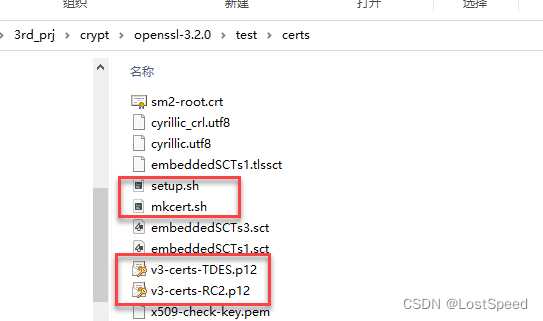
openssl3.2 - 官方demo学习 - test - certs
文章目录 openssl3.2 - 官方demo学习 - test - certs概述笔记.sh的执行语句打印的方法要修改的实际函数END openssl3.2 - 官方demo学习 - test - certs 概述 官方demos目录有证书操作的例子 已经做了笔记 openssl3.2 - 官方demo学习 - certs 但是这个demos/certs目录的脚本,…...
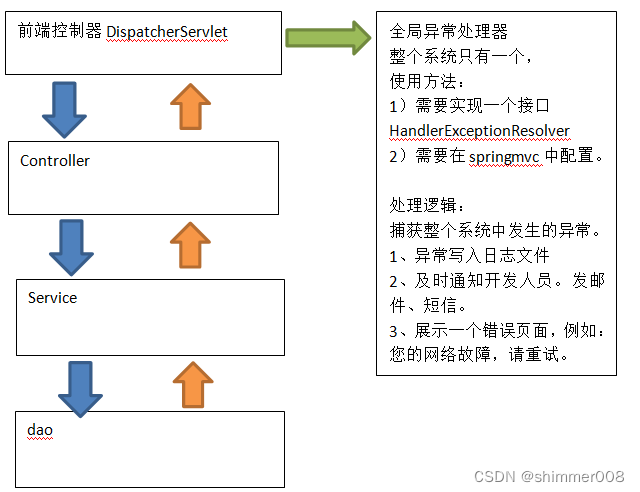
Spring MVC学习之——异常处理器
异常处理器 如果不加以异常处理,错误信息肯定会抛在浏览器页面上,这样很不友好,所以必须进行异常处理。 1.异常处理思路 系统的dao、service、controller出现都通过throws Exception向上抛出,最后由springmvc前端控制器交由异常…...
:HMAC Authentication)
HTTP API 认证技术详解(四):HMAC Authentication
目录 什么是 HMAC Authentication 认证 HMAC Authentication 原理 HMAC Authentication 认证的步骤 使用 Golang 实现 HMAC Authentication 认证 HMAC Authentication 认证的安全性 HMAC 认证的最佳实践 小结 HTTP API 认证技术主要用于验证客户端身份,并确保…...
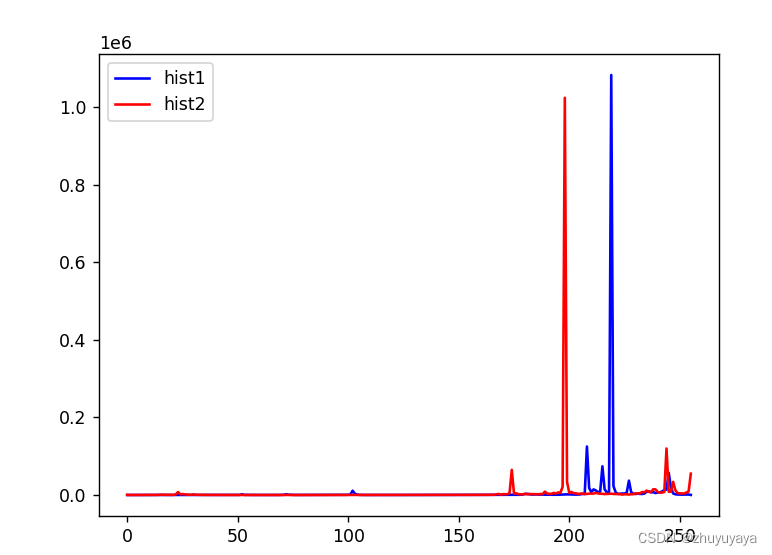
如何绘制出图像的色素分布直方图
效果 如图,可以展示出我们的图像的颜色分布直方图,表明的图像的亮和暗 实现可视化色素分布直方图方法 这里我们对我们的灰色图片和彩色图片进行了直方图显示 import cv2 import matplotlib.pyplot as plt image cv2.imread("test.jpg") # 彩色图片->…...

esp32-c-简单应用笔记
1、资料 ESP32 开发环境 Espressif-IDE: https://blog.csdn.net/chuner0425/article/details/123466848 https://blog.csdn.net/bin_zhang1/article/details/129993820?utm_mediumdistribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-1299938…...

What is `XSS` does?
跨站脚本攻击(Cross-Site Scripting,XSS)是一种针对网站应用程序的安全漏洞,允许攻击者将恶意脚本注入到其他用户查看的网页中。当这些用户访问受感染的页面时,他们的浏览器会执行这些恶意脚本,导致各种安全…...
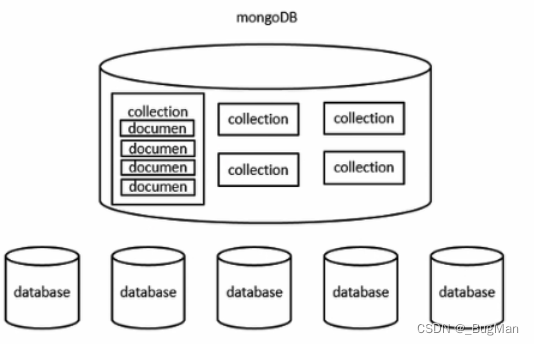
【文档数据库】ES和MongoDB的对比
目录 1.由文档存储牵出的问题 2.什么是MongoDB? 3.ES和MongoDB的对比 1.由文档存储牵出的问题 本文或者说关于mongodb的这个系列文章的源头: 前面我们聊过了分布式链路追踪系统,在基于日志实现的分布式链路追踪的方式seluthzipkin中为了…...

VUE工程化项目--vue组件化
组件化开发 & 根组件 : ① 组件化: 一个页面可以拆分成 一个个组件 ,每个组件有着自己独立的 结构、样式、行为 。 好处:便于 维护 ,利于 复用 → 提升 开发效率 。 组件分类:普通组件、根组件。 …...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
