电子技术——CMOS反相器
电子技术——CMOS反相器

在本节,我们深入学习CMOS反相器。
电路原理
下图是我们要研究的CMOS反相器的原理图:
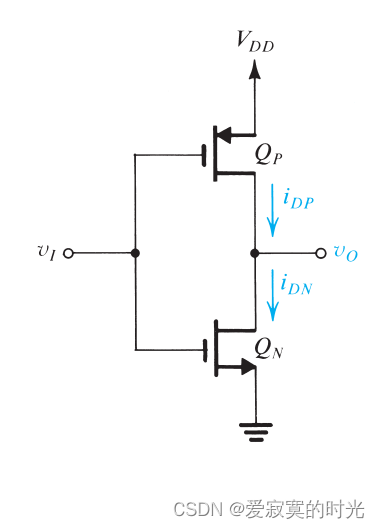
下图展示了当输入 vI=VDDv_I = V_{DD}vI=VDD 时的 iD−vDSi_D-v_{DS}iD−vDS 曲线:
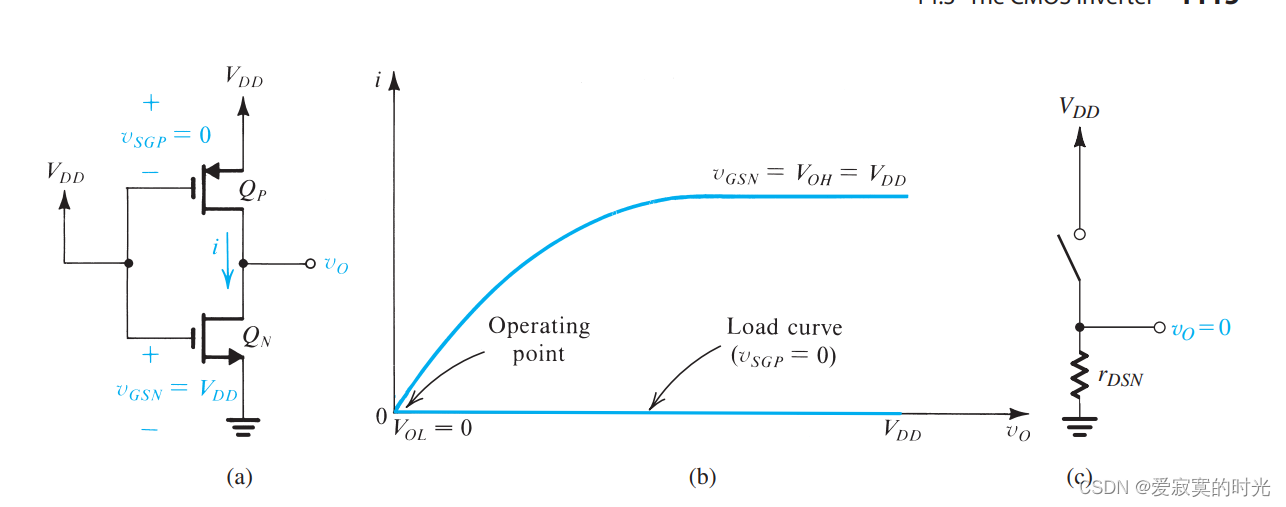
我们把 QNQ_NQN 当做是驱动源,而 QPQ_PQP 作为负载,我们在图像上叠加关于 QPQ_PQP 在 vSGP=0v_{SGP} = 0vSGP=0 的负载曲线。因为 vSGP<∣Vt∣v_{SGP} < |V_t|vSGP<∣Vt∣ 因此负载曲线是一条零电流的水平直线。两个曲线的交点就是我们的工作点,我们发现此时电流为零,输出电压为零。同样意味着此时耗散功率为零。然而,工作点处在曲线 iD−vDSi_D-v_{DS}iD−vDS 的上升处,具有有限的斜率,因此 QNQ_NQN 对外表现出有限的阻抗,如图©:
rDSN=1/[kn′(WL)n(VDD−Vtn)]r_{DSN} = 1 / [k_n'(\frac{W}{L})_n (V_{DD} - V_{tn})] rDSN=1/[kn′(LW)n(VDD−Vtn)]
另外一种情况,当输入 vI=0v_I = 0vI=0 的时候,如图:

因为 vGSN=0v_{GSN} = 0vGSN=0 此时驱动曲线是一条零电流的直线,此时负载曲线是 vSGP=VDDv_{SGP} = V_{DD}vSGP=VDD 的曲线。我们发现,此时交点在零电流,输出电压为 vO=VDDv_O = V_{DD}vO=VDD 。耗散功率为零。同样的,QPQ_PQP 表现出有限的阻抗:
rDSP=1/[kp′(WL)p(VDD−∣Vtp∣)]r_{DSP} = 1 / [k_p' (\frac{W}{L})_p (V_{DD} - |V_{tp}|)] rDSP=1/[kp′(LW)p(VDD−∣Vtp∣)]
虽然,静态电流为零,这种CMOS反相器可以提供较大的负载能力。例如,负载是容性负载的时候,当 QNQ_NQN 导通的时候,由于其较小的开关阻抗,可以提供一个较短的对地回路,可以使得容性负载迅速泄放电荷,拉低电位,因此 QNQ_NQN 称为下拉元件。同样的,当 QPQ_PQP 导通的时候,由于其较小的开关阻抗,可以提供一个较短的对电压通路,可以使得容性负载迅速充满电荷,拉高电位,因此 QPQ_PQP 称为上拉元件。
根据上面的讨论CMOS反相器作为理想的反相器:
- 输出电压的范围在 0−VDD0-V_{DD}0−VDD 电压压摆达到最大。同时,两个MOS可以进行匹配使得提供一个对称的电压传导特性,具有较宽的噪声容限。
- 静态功率为零,这是因为电压源和地直接没有直接的DC回路。
- 对地和电压都是低阻抗路径,较低的输出阻抗使得反相器具有较高的驱动能力,以及实现电气功能与元件参数无关,提高噪声和其他干扰的容忍性。
- 上拉的下拉元件使得电路的翻转速度更快,对于容性负载具有较高的驱动能力。
- 输入阻抗为无穷大。所以CMOS反相器可以驱动大量同样的CMOS反相器而不造成电压水平损失。当然,增加被驱动元件的数量就意味着增加了容性负载,这会降低电平的翻转速度。
电压传导特性
通过联立两个曲线,我们可以绘制出CMOS反相器的电压传导特性曲线,这里给出驱动和负载方程:
iDN=kn′(WL)n[(vI−Vtn)vO−12vO2],vO≤vI−Vtni_{DN} = k_n'(\frac{W}{L})_n [(v_I - V_{tn})v_O - \frac{1}{2}v_O^2], v_O \le v_I - V_{tn} iDN=kn′(LW)n[(vI−Vtn)vO−21vO2],vO≤vI−Vtn
iDN=12kn′(WL)n(vI−Vtn)2,vO≥vI−Vtni_{DN} = \frac{1}{2}k_n' (\frac{W}{L})_n (v_I - V_{tn})^2, v_O \ge v_I - V_{tn} iDN=21kn′(LW)n(vI−Vtn)2,vO≥vI−Vtn
iDP=kp′(WL)p[(VDD−vI−∣Vtp∣)(VDD−vO)−12(VDD−vO)2],vO≥vI+∣Vtp∣i_{DP} = k_p' (\frac{W}{L})_p [(V_{DD} - v_I - |V_{tp}|)(V_{DD} - v_O) - \frac{1}{2}(V_{DD} - v_O)^2], v_O \ge v_I + |V_{tp}| iDP=kp′(LW)p[(VDD−vI−∣Vtp∣)(VDD−vO)−21(VDD−vO)2],vO≥vI+∣Vtp∣
iDP=12kp′(WL)p(VDD−vI−∣Vtp∣)2,vO≤vI+∣Vtp∣i_{DP} = \frac{1}{2} k_p' (\frac{W}{L})_p(V_{DD} - v_I - |V_{tp}|)^2, v_O \le v_I + |V_{tp}| iDP=21kp′(LW)p(VDD−vI−∣Vtp∣)2,vO≤vI+∣Vtp∣
通常电路设计者通常将阈值电压设计为 Vtn=∣Vtp∣=VtV_{tn} = |V_{tp}| = V_tVtn=∣Vtp∣=Vt 。同样,尽管并不总是这样,我们也假设两个MOS完全匹配,即 kn′(W/L)n=kp′(W/L)pk_n'(W/L)_n = k_p'(W/L)_pkn′(W/L)n=kp′(W/L)p 。因为存在电子速率差异,当两个MOS具有相同的长度的时候,其宽度满足:
WpWn=μnμp\frac{W_p}{W_n} = \frac{\mu_n}{\mu_p} WnWp=μpμn
此时电路具有对称的传递特性,以及相同的负载驱动能力。电压传导特性如图:
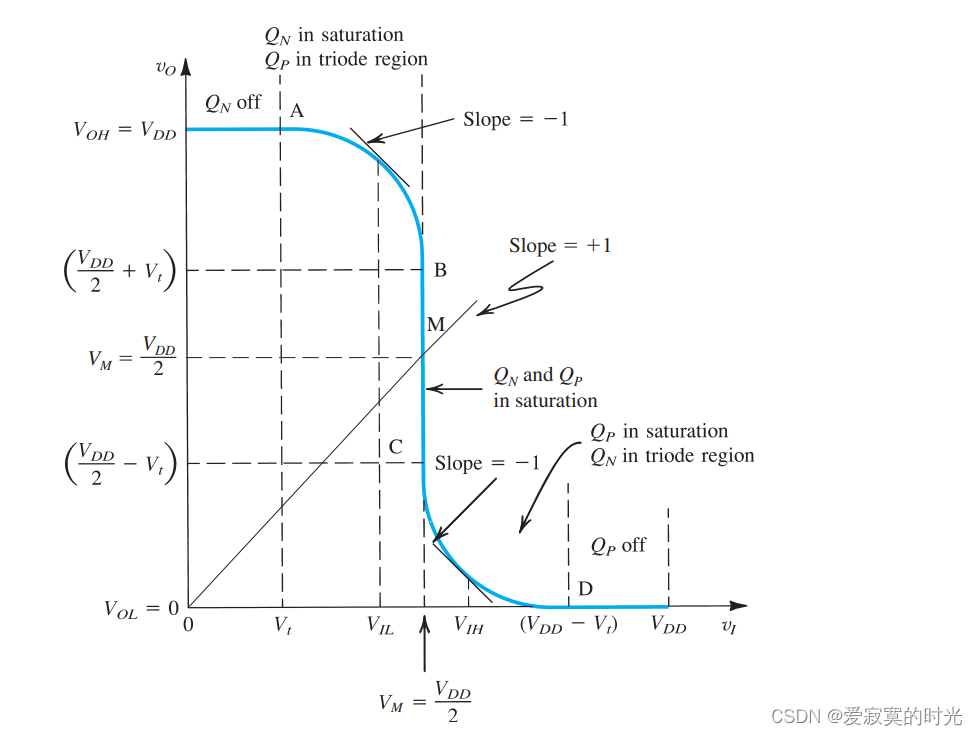
其中BC段为MOS的放大器区,因为我们忽略了沟道宽度调制效应,因此在BC端具有无限大的增益。由于电路的对称性,传导中点发生在 VM=VDD/2V_M = V_{DD} / 2VM=VDD/2 的地方,上下边界点为 vO(B)=VDD/2+Vtv_O(B) = V_{DD} / 2 + V_tvO(B)=VDD/2+Vt (QPQ_PQP 进入三极管区) 以及 vO(C)=VDD/2−Vtv_O(C) = V_{DD} / 2 -V_tvO(C)=VDD/2−Vt(QNQ_NQN 进入三极管区)。
为了决定点 VIHV_{IH}VIH 的位置,我们注意到此时 QNQ_NQN 进入三极管区,通过电流相等我们联立方程:
(vI−Vt)vO−12vO2=12(VDD−vI−Vt)2(v_I - V_t)v_O - \frac{1}{2} v_O^2 = \frac{1}{2} (V_{DD} - v_I - V_t)^2 (vI−Vt)vO−21vO2=21(VDD−vI−Vt)2
对 vOv_OvO 求导可得:
(vI−Vt)dvOdvI+vO−vOdvOdvI=−(VDD−vI−Vt)(v_I - V_t) \frac{dv_O}{dv_I} + v_O - v_O \frac{dv_O}{dv_I} = -(V_{DD} - v_I - V_t) (vI−Vt)dvIdvO+vO−vOdvIdvO=−(VDD−vI−Vt)
带入 vI=VIHv_I = V_{IH}vI=VIH 以及 dvOdvI=−1\frac{dv_O}{dv_I} = -1dvIdvO=−1 我们得到:
vO=VIH−VDD2v_O = V_{IH} - \frac{V_{DD}}{2} vO=VIH−2VDD
带入 vI=VIHv_I = V_{IH}vI=VIH 得到 vOv_OvO 带回上式得到:
VIH=18(5VDD−2Vt)V_{IH} = \frac{1}{8} (5V_{DD} - 2V_t) VIH=81(5VDD−2Vt)
同样的做法我们得到:
VIL=18(3VDD+2Vt)V_{IL} = \frac{1}{8} (3V_{DD} + 2V_t) VIL=81(3VDD+2Vt)
可以计算出噪声容限:
NMH=VOH−VIH=18(3VDD+2Vt)NM_H = V_{OH} - V_{IH} = \frac{1}{8}(3V_{DD} + 2V_t) NMH=VOH−VIH=81(3VDD+2Vt)
NML=VIL−VOL=18(3VDD+2Vt)NM_L = V_{IL} - V_{OL} = \frac{1}{8}(3V_{DD} + 2V_t) NML=VIL−VOL=81(3VDD+2Vt)
正如期望的那样,若两个MOS完全一样,则此时传导特性完全对称。
MOS不完全匹配的情况
若我们想使得MOS完全匹配,那么PMOS器件的尺寸就要是NMOS尺寸的3到4倍。这会导致更大的硅区域。一方面浪费了一些硅区域,为器件小型化造成了不利条件,另一方面增加了器件的容性阻抗,增加了CMOS反相器的时间延迟。因此,通常情况下MOS是不完全匹配。
首先我们推导不完全匹配下的M点,因为两个MOS都工作在饱和区,因此带入 vI=vO=VMv_I = v_O = V_MvI=vO=VM 我们得到:
VM=r(VDD−∣Vtp∣)+Vtnr+1V_M = \frac{r(V_{DD} - |V_{tp}|) + V_{tn}}{r + 1} VM=r+1r(VDD−∣Vtp∣)+Vtn
这里:
r=kpkn=μpWpμnWnr = \sqrt{\frac{k_p}{k_n}} = \sqrt{\frac{\mu_p W_p}{\mu_n W_n}} r=knkp=μnWnμpWp
这里我们让 LLL 的长度相同,通常是在指定工艺下的最小精度值,注意到当MOS完全匹配的时候,此时 r=1r = 1r=1 。对于 ∣Vtp∣=Vtn|V_{tp}| = V_{tn}∣Vtp∣=Vtn 并且 r=1r = 1r=1 产生 VM=VDD/2V_M = V_{DD} / 2VM=VDD/2 。对于给定 VDDV_{DD}VDD 和 VtnV_{tn}Vtn 以及 VtpV_{tp}Vtp 则 VMV_MVM 是一个和工艺参数 rrr 相关的函数。例如,在0.18um工艺下:

我们可以总结关键两点:
- VMV_MVM 随着 rrr 的增大而增大。因此,让 kp>knk_p > k_nkp>kn 则 VMV_MVM 向 VDDV_{DD}VDD 偏移,让 kp<knk_p < k_nkp<kn 则 VMV_MVM 向 000 偏移。
- VMV_MVM 并不是与 rrr 强相关,例如让 rrr 降低两倍,则 VMV_MVM 降低0.13V。
第2条告诉我们,若我们能够接受极小的 NMLNM_LNML 减小和 VMV_MVM 点偏移,我们可以不让MOS完全匹配,从而提高器件性能等等。
相关文章:

电子技术——CMOS反相器
电子技术——CMOS反相器 在本节,我们深入学习CMOS反相器。 电路原理 下图是我们要研究的CMOS反相器的原理图: 下图展示了当输入 vIVDDv_I V_{DD}vIVDD 时的 iD−vDSi_D-v_{DS}iD−vDS 曲线: 我们把 QNQ_NQN 当做是驱动源&#x…...
)
gazebo仿真轨迹规划+跟踪(不在move_base框架下)
以Tianbot为例子,开源代码如下: https://github.com/tianbot/tianbot_mini GitHub - tianbot/abc_swarm: Ant Bee Cooperative Swarm, indicating air-ground cooperation. This repository is for Tianbot Mini and RoboMaster TT swarm kit. 1.在…...

C. Good Subarrays(前缀和)
C. Good Subarrays一、问题二、分析三、代码一、问题 二、分析 这道题目的意思就是给我们一个数组,然后我们从数组中选取一个连续的区间,这个区间满足条件:区间内的元素和等于区间的长度。 对于区间和问题我们先想到的是前缀和的算法。 那…...
关于Facebook Messenger CRM,这里有你想要知道的一切
关于Facebook Messenger CRM,这里有你想要知道的一切!想把Facebook Messenger与你的CRM整合起来吗?这篇博文是为你准备的! 我们将介绍有关获得Facebook Messenger CRM整合的一切信息。然后,我们将解释为什么你需要像SaleSmartly&a…...
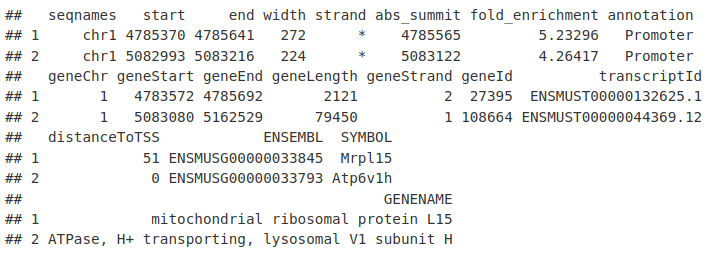
ChIP-seq 分析:数据与Peak 基因注释(10)
动动发财的小手,点个赞吧! 1. 数据 今天,我们将继续回顾我们在上一次中研究的 Myc ChIPseq。这包括用于 MEL 和 Ch12 细胞系的 Myc ChIPseq。 可在此处[1]找到 MEL 细胞系中 Myc ChIPseq 的信息和文件可在此处[2]找到 Ch12 细胞系中 Myc ChIP…...
)
《C++ Primer Plus》第18章:探讨 C++ 新标准(8)
使用大括号括起的初始化列表语法重写下述代码。重写后的代码不应使用数组 ar: class Z200 { private:int j;char ch;double z; public:Z200(int jv, char chv, zv) : j(jv), ch(chv), z(zv) {} ... };double x 8.8; std::string s "What a bracing effect!&q…...
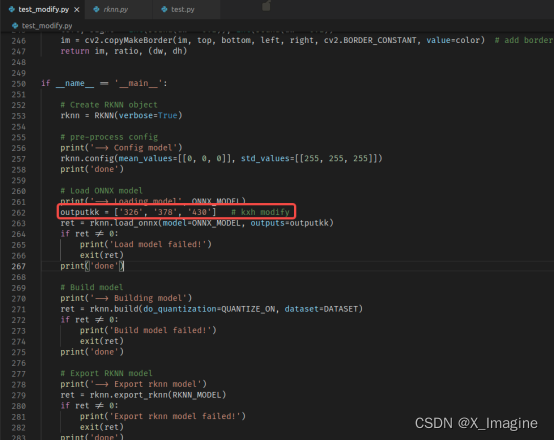
YOLO-V5 系列算法和代码解析(八)—— 模型移植
文章目录工程目标芯片参数查阅官方文档基本流程Python 版工具链安装RKNPU2的编译以及使用方法移植自己训练的模型工程目标 将自己训练的目标检测模型【YOLO-V5s】移植到瑞芯微【3566】芯片平台,使用NPU推理,最终得到正确的结果。整个过程涉及模型量化、…...

js实现复制拷贝的兼容方法
1. 定义复制拷贝的方法 在某个工具类方法中定义该方法,兼容不同浏览器处理 /*** description 拷贝的类方法*/ class CopyClass {// constructor() {}setRange(input) {return new Promise((resolve, reject) > {try {// 创建range对象const range document.c…...
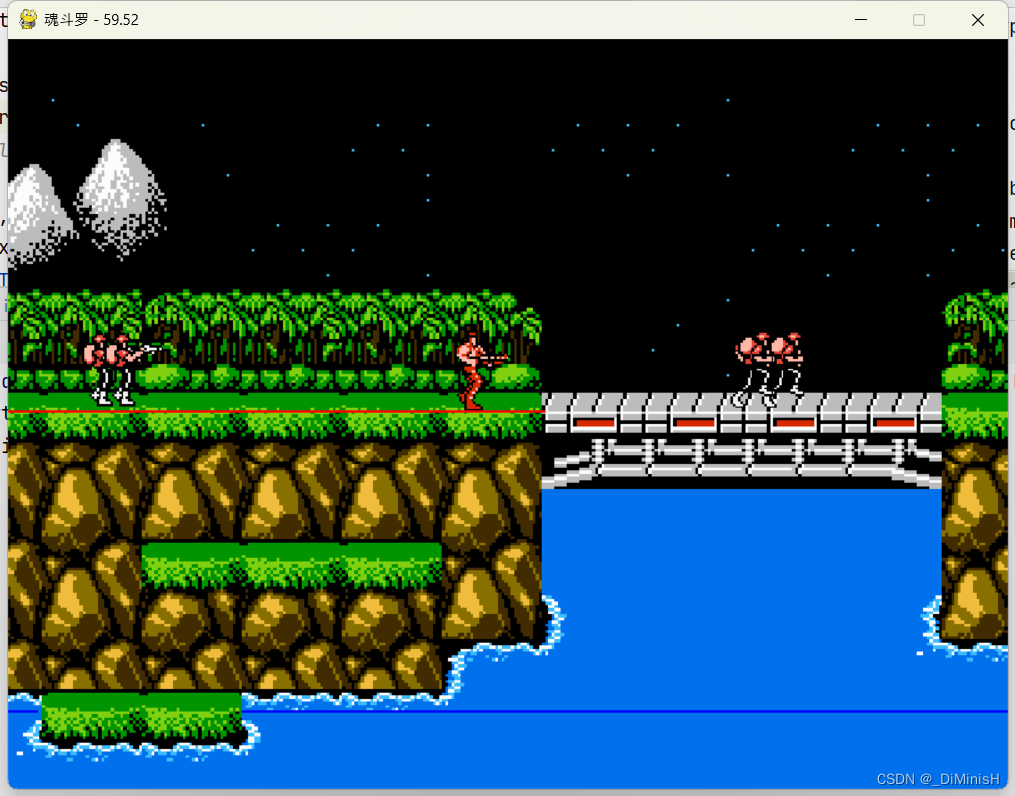
学习 Python 之 Pygame 开发魂斗罗(八)
学习 Python 之 Pygame 开发魂斗罗(八)继续编写魂斗罗1. 创建敌人类2. 增加敌人移动和显示函数3. 敌人开火4. 修改主函数5. 产生敌人6. 使敌人移动继续编写魂斗罗 在上次的博客学习 Python 之 Pygame 开发魂斗罗(七)中࿰…...
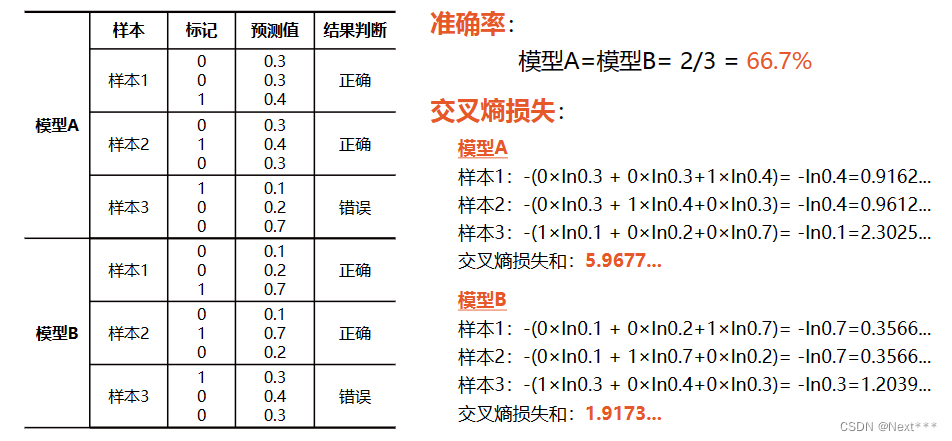
Lesson11---分类问题
11.1 逻辑回归 11.1.1 广义线性回归 课程回顾 线性回归:将自变量和因变量之间的关系,用线性模型来表示;根据已知的样本数据,对未来的、或者未知的数据进行估计 11.1.2 逻辑回归 11.1.2.1 分类问题 分类问题:垃圾…...

Python基础学习12——异常
在Python中,会使用“异常”这个十分特殊的对象来管理程序执行期间发生的错误,即报错。本文将介绍一下python基础的处理异常的方法以及一些基本的异常类型。 异常处理方法 try-except代码块 当我们编写程序时,我们可以编写一个try-except代…...

[日常练习]练习17:链表头插法、尾插法练习
[日常练习]练习17:链表头插法、尾插法练习练习17描述输入输出输入示例1输出示例1输入示例2输出示例2代码演示:总结练习17 【日常练习】 链表头插法、尾插法练习 描述 输入3 4 5 6 7 9999一串整数,9999代表结束,通过头插法新建链…...
第十四届蓝桥杯模拟赛(第三期)试题与题解 C++
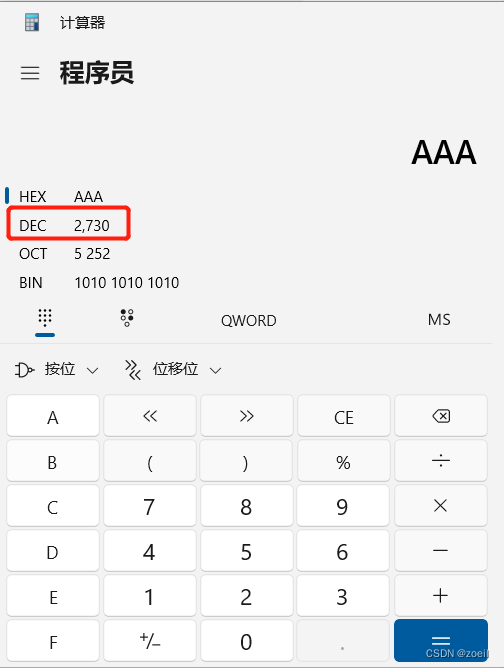
目录 一、填空题 (一)最小的十六进制(答案:2730) (二)Excel的列(答案:BYT) (三)相等日期(答案:70910) (四)多少种取法(答案:189)…...

关于 “宏“
起源 宏 Macro"这个词源于希腊语 “makros”,意为“大的,长的” 延伸使用 随后用于计算机领域是,在汇编语言时用于描述一大堆的汇编指令。 只要用宏指令,就是直接用的一大堆的汇编指令(有点函数的味道…...

1.2 CSS标签选择器,类选择器
CSS选择器: 根据不同的需求选出不同的标签,进行美化装饰 1. 标签选择器 标签选择器(元素选择器):用 HTML标签名作为选择器,按标签名称进行分类,为页面某一类标签指定统一的CSS样式 作用: 可以把某一类标签全部选中&…...

【Linux】进程等待 | 详解 wait/waitpid 的 status 参数
🤣 爆笑教程 👉 《看表情包学Linux》👈 猛戳订阅 🔥 💭 写在前面:在上一章中我们讲解了进程创建与进程终止,本章我们开始讲解进程等待。进程等待这部分知识相较于前面还是较为复杂的࿰…...

OpenAI眼中的无线调优策略
问:无线调优策略该怎么优化无线调优是指对无线网络的各种参数进行优化,以提高网络性能和用户体验。以下是几个无线调优策略:频谱分配:通过优化频谱的分配,可以提高网络的容量和覆盖范围。在频谱分配时,需要…...
DataX入门
目录 1. DataX介绍 2. DataX支持的常用数据源类型 3. 设计理念 4. DataX框架设计 4.1. Reader 4.2. Writer 4.3. Framework 5. DataX的运行流程 6. DataX与Sqoop对比 7. 部署 8. 配置详解 9. 案例 同步MySql到HDFS 9.1. 整体结构 9.2. mySqlReader 9.2.1. …...

第二章SpringBoot基础学习
文章目录SpringBoot依赖管理特性依赖管理开发导入starter场景启动器SpringBoot自动配置特性自动配好Tomcat自动配好SpringMVC默认的包结构各种配置拥有默认值按需加载所有自动配置项SpringBoot注解底层注解ConfigurationImport导入组件Conditional条件装配ImportResource导入Sp…...

B - Build Roads (最小生成树 + 打表)
https://vjudge.net/problem/Gym-103118B/origin 在猫的国度里,有n个城市。猫国国王想要修n -1条路来连接所有的城市。第i市有一家ai经验价值的建筑公司。要在第i市和第j市之间修建公路,两个城市的建筑公司需要相互合作。但是,在修路的过程中…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
