5396. 棋盘
5396. 棋盘 - AcWing题库
二维差分数组
#include <iostream>
#include <vector>
using namespace std;int main() {int n, m;cin >> n >> m;vector<vector<int>> v(n + 2, vector<int>(n + 2));while (m--) {int x1, x2, y1, y2;cin >> x1 >> y1 >> x2 >> y2;v[x1][y1]++, v[x2 + 1][y2 + 1]++;v[x1][y2 + 1]--, v[x2 + 1][y1]--;}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {v[i][j] = v[i][j] + v[i - 1][j] + v[i][j - 1] - v[i - 1][j - 1];cout << v[i][j] % 2;}cout << endl;}return 0;
}相关文章:

5396. 棋盘
5396. 棋盘 - AcWing题库 二维差分数组 #include <iostream> #include <vector> using namespace std;int main() {int n, m;cin >> n >> m;vector<vector<int>> v(n 2, vector<int>(n 2));while (m--) {int x1, x2, y1, y2;cin…...
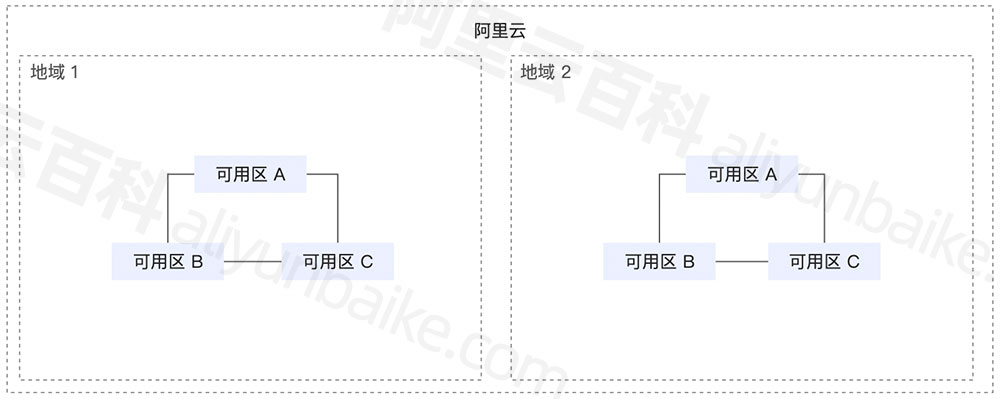
阿里云地域和可用区分布表,2024更新
2024年阿里云服务器地域分布表,地域指数据中心所在的地理区域,通常按照数据中心所在的城市划分,例如华北2(北京)地域表示数据中心所在的城市是北京。阿里云地域分为四部分即中国、亚太其他国家、欧洲与美洲和中东&…...

Pandas实战100例 | 案例 49: 数值运算
案例 49: 数值运算 知识点讲解 Pandas 提供了进行基本数学运算的简便方法,允许你在 DataFrame 的列之间执行加法、减法、乘法和除法等操作。 数值运算: 直接对 DataFrame 的列应用算术运算符(+, -, *, /)可以执行相应的数值运算。示例代码 # 准备数据和示例代码的运行结果…...
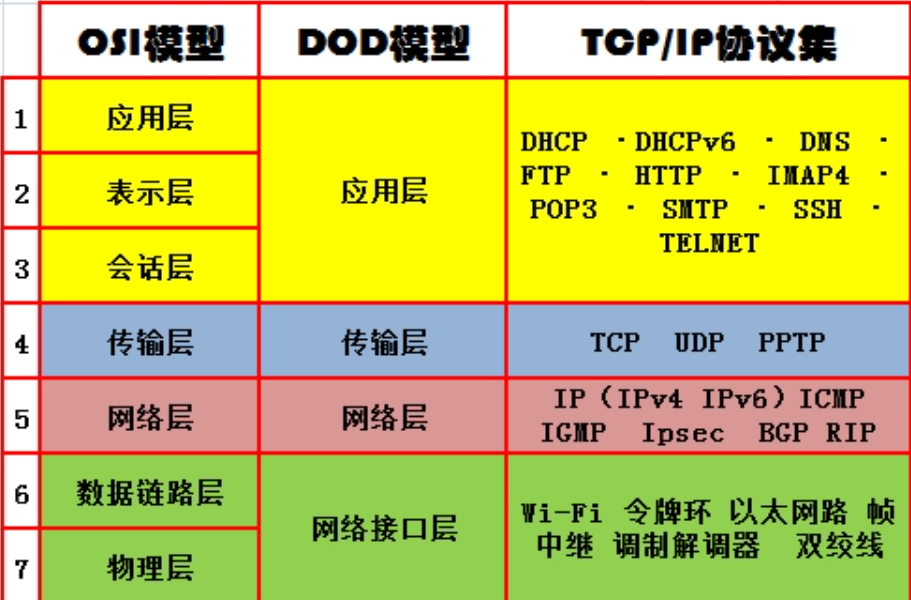
OSI七层协议和五层协议
【 1 】互联网协议交互的基础 硬件设备 光缆 【 2 】OSI七层协议 物理层(Physical Layer):负责传输比特流(0和1)以及物理连接的建立和维护。数据链路层(Data Link Layer):提供可…...
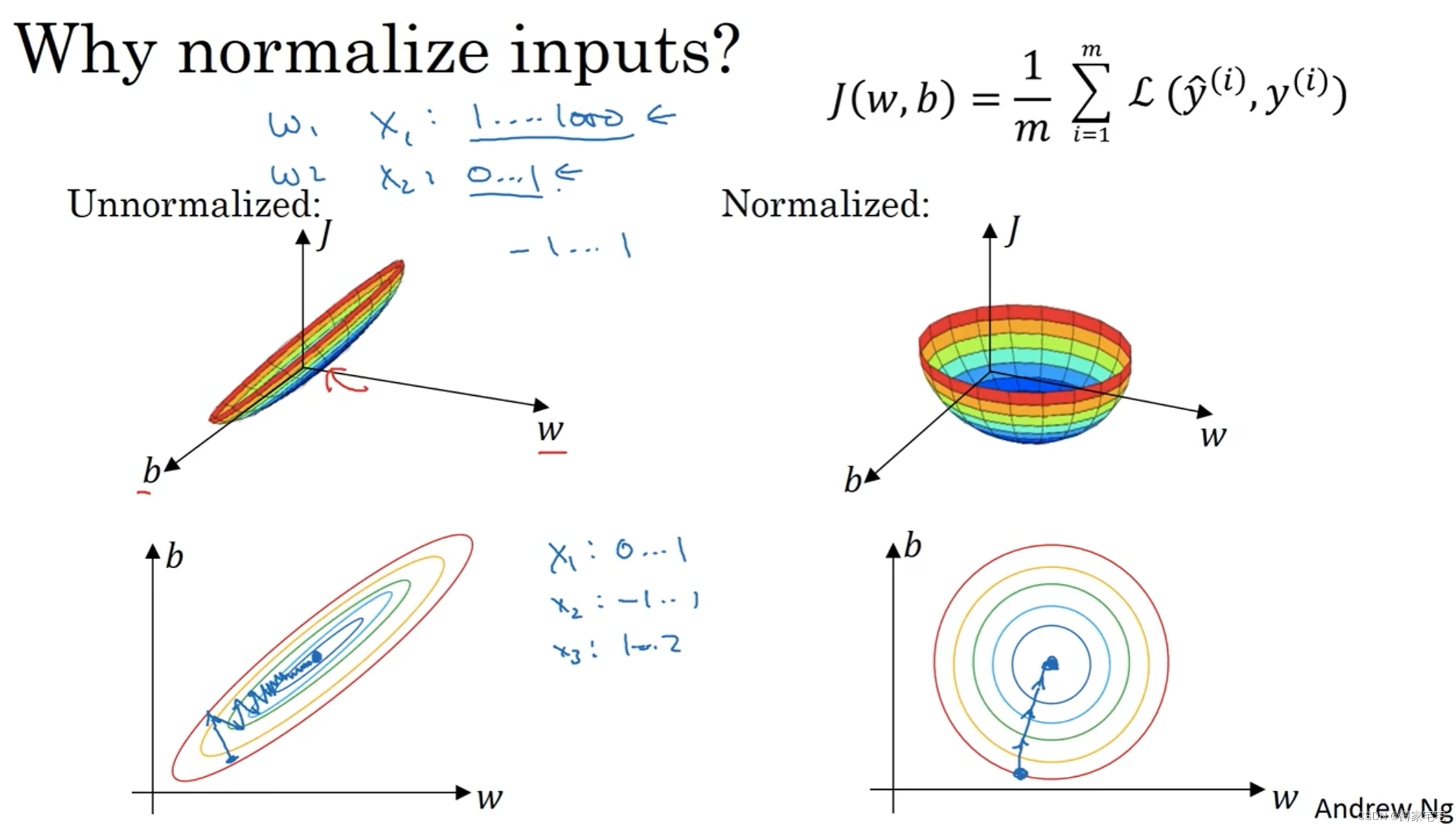
深度学习记录--归—化输入特征
归化 归化输入(normalizing inputs),对特征值进行一定的处理,可以加速神经网络训练速度 步骤 零均值化 通过x值更新让均值稳定在零附近,即为零均值化 归化方差 适当减小变量方差 解释 归化可以让原本狭长的数据图像变得规整,梯度下降的…...

Go Build编译打包文件
Go编译打包文件 1、简单打包 程序 main1.go: package mainimport "fmt"func main() {fmt.Println("Hello World!") }打包: # 在linux服务上执行下面的3个命令 # linux平台,生成main1可执行程序 CGO_ENABLED0 GOOSlinux GOARCHam…...
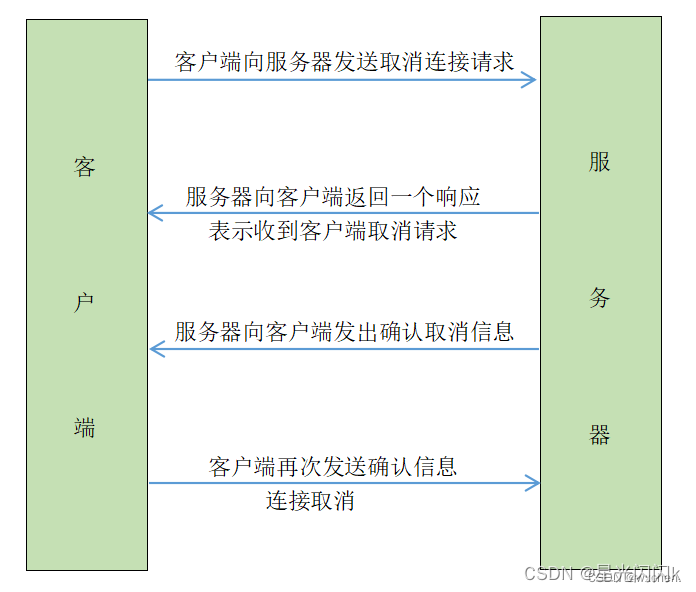
Java网络编程:概述--快速入门
I. 介绍 1.1 什么是网络编程 - 网络编程是指通过计算机网络实现程序之间的通信。在Java中,网络编程通常涉及到数据的传输、通信协议的使用以及与网络相关的各种操作。 1.2. 为什么学习Java网络编程 - Java网络编程是Java开发者重要的技能之一,因为它允许…...

linux配置DNS主从服务器
实验设备 主服务器:OpenElur Linux IP地址为192.168.188.129 从服务器:RedHat Linux IP地址为192.168.188.128 实验步骤 1.进行主服务器的基础配置 #安装DNS对应工具 [rootOpenElurRJW ~]# yum install bind -y#编辑DNS系统配置信息 [rootOpenElurRJW ~]# cat /etc/named.…...

Day34 贪心算法 part03 1005. K 次取反后最大化的数组和 134. 加油站 135. 分发糖果
贪心算法 part03 1005. K 次取反后最大化的数组和 134. 加油站 135. 分发糖果 1005. K 次取反后最大化的数组和 思路 第一步,从前向后遍历,遇到负数将其变为正数,同时K–第二步:如果K还大于0,那么反复转变数值最小的…...

最全对象存储(云盘)挂载本地主机或服务器
1.对象存储介绍 1.1 分类 分布式存储的应用场景相对于其存储接口,现在流行分为三种: 块存储: 这种接口通常以QEMU Driver或者Kernel Module的方式存在,这种接口需要实现Linux的Block Device的接口或者QEMU提供的Block Driver接口,块存储一般…...

24校招,江淮汽车软件测试工程师技术面+HR面
前言 记录一下楼主的面试经历,希望对后来者有用 时间:15min 平台:腾讯会议 过程 技术面试 自我介绍 为啥不考研 实习收获 你有做过软件开发的工作吗? 除了Java和Python,还会其他的语言吗? 学过C吗…...
从零开始学习Zeppelin:大数据可视化分析的交互式开发系统!
介绍:Apache Zeppelin是一个基于Web的交互式开发系统,主要用于进行大数据可视化分析。其核心概念是notebook,所有的操作都可以在notebook中完成。Zeppelin提供了一套非常全面的数据分析解决方案,支持数据采集、数据发现、数据分析…...

VCG 曲面重建之滚球算法
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 滚球算法(BPA)是一种与alpha形状相关的曲面重建方法。直观地想象一个具有给定半径的3D球,我们把它扔在点云上。如果它击中任何3个点(并且它没有穿过这3个点),它就创造了一个三角形。然后,算法从现有三角形的边缘…...
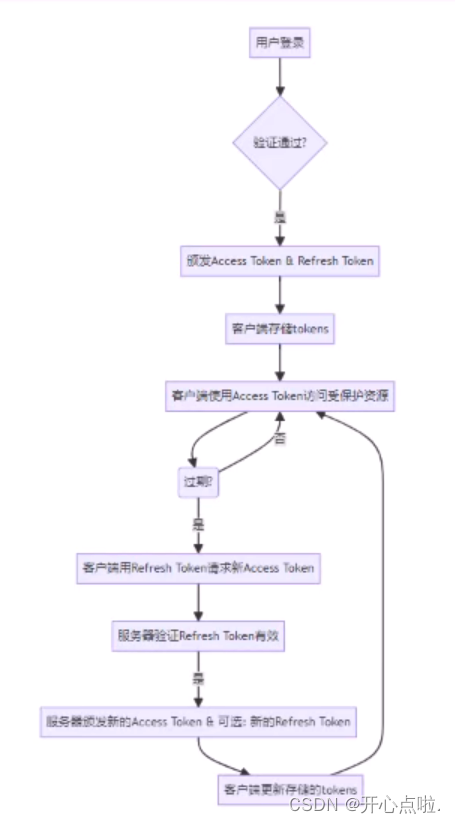
为什么使用双token实现无感刷新用户认证?
单token机制 认证机制:对与单token的认证机制在我们项目中仅使用一个Access Token的访问令牌进行用户身份认证和授权的方案处理。 不足之处: 安全性较低(因为只有一个token在客户端和服务器端之间进行传递,一目Acess Token被截获或者被泄露…...

论文阅读 Self-Supervised Burst Super-Resolution
这是一篇 ICCV 2023 的文章,主要介绍的是用自监督的方式进行多帧超分的学习 Abstract 这篇文章介绍了一种基于自监督的学习方式来进行多帧超分的任务,这种方法只需要原始的带噪的低分辨率的图。它不需要利用模拟退化的方法来构造数据,而且模…...
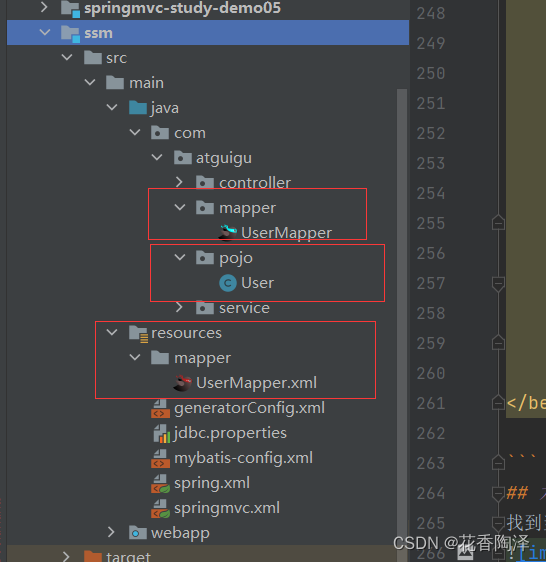
Spring+SpringMVC+Mybatis进行项目的整合
Spring SpringMVCM Mybatis 整合 一、 通过idea创建maven工程 二、 引入依赖项以及导入mybatis逆向工程的插件 将如下的文件替换所在工程的pom文件 <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4…...
vue3 实现简单计数器示例——一个html文件展示vue3的效果
目的:作为一个新手开发,我想使用 Vue 3 将代码封装在 HTML 文件中时,进行界面打开展示。 一、vue计数示例 学了一个简单计数器界面展示,代码如下: <!DOCTYPE html> <html lang"en"><head&…...
)
面试经典150题(88-89)
leetcode 150道题 计划花两个月时候刷完,今天(第四十四天)完成了2道(88-89)150: 88.(22. 括号生成) 题目描述: 数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效…...
【设计模式-3.3】结构型——享元模式
说明:说明:本文介绍设计模式中结构型设计模式中的,享元模式; 游戏地图 在一些闯关类的游戏,如超级玛丽、坦克大战里面,游戏的背景每一个关卡都不相同,但仔细观察可以发现,其都是用…...

【征服redis6】Redis的内存淘汰详解
目录 1.redis的基本策略 2.Redis中的缓存淘汰策略 3.Redis内存不足的情况 4.几种淘汰策略的实现原理 5.项目实践与优化策略 5.1 配置案例 5.2 项目优化策略参考 数据库存储会将数据保存到磁盘中,而Redis的核心数据是在内存中的,而Redis本身主要用来…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
