【算法】递归
递归
- 递归
- 初始递归:数列求和
- 递归的应用:任意进制转换
- 递归深度限制
- 递归可视化:分形树
- 递归可视化:谢尔宾斯基Sierpinski三角形
- 递归的应用:汉诺塔
- 递归的应用:探索迷宫
- 分治策略和递归
- 优化问题
- 兑换最少个数硬币问题
- 贪心策略
递归
递归是一种解决问题的方法,其精髓在于将问题分解为规模更小的相同问题,持续分解,直到问题规模小到可以用飞常简单直接的方式来解决。
递归的问题分解方式非常独特,其算法方面的明显特征就是:在算法流程中调用自身。
递归为我们提供了一种对复杂问题的优雅解决方案。
函数自己调用自己,形如:
int f(int x){xxxxxxxxxxxxxxxreturn f(x-1);
}
初始递归:数列求和
问题:给定一个列表,返回所有数的和
列表中数的个数不定,需要一个循环和一个累加变量来迭代求和
既不能用for,也不能用while,对不确定长度的列表求和
def listsum(numList):theSum=0for i in numList:theSum=theSum+ireturn theSumprint(listsum([1,3,5,7,9]))
求和实际上由一次次的加法实现,而加法恰有2个操作数
将问题规模较大的列表求和,分解为规模较小而且固定的2个数求和
数列求和问题首先具备了基本结束条件:当
递归的应用:任意进制转换
整数转换为任意进制
十进制有10个不同符号:convString=“0123456789”
比10小的整数转换成十进制,直接查表:convString[n]
比10大的整数,拆成一系列比10小的整数,逐个查表,如769,拆成7、6、9
递归三定律里,基本结束条件为:小于10的整数;拆解整数的过程就是向“基本结束条件”演进的过程
用整数除,和求余数两个计算将整数一步步拆开
除以“进制基base”://base
对“进制基”求余数:%base
问题分解为:余数总小于“进制基base”,是基本结束条件,可直接进行查表转换
整数商成为“更小规模”问题,通过递归调用自身解决
def toStr(n,base):convertString="0123456789ABCDEF"if n<base:return convertString[n]else:return toStr(n//base,base)+convertString[n%base]print(toStr(1453,16))
当一个函数被调用的时候,系统会把调用时的现场数据压入到系统调用栈
每次调用,压入栈的现场数据称为栈帧
当函数返回时,要从调用栈的栈顶取得返回地址,恢复现场,弹出栈帧,按地址返回
递归深度限制
RecursionError
检查是否忘记设置基本结束条件,导致无限递归。
或者向基本结束条件演进太慢,导致递归层数太多,调用栈溢出
def tell_story():
在Python内置的sys模块可以获取和调整最大递归深度
递归可视化:分形树
Python的海龟作图系统tuetle moudle
import turtle
t=turtle.Turtle()
# 作图开始
for i in range(4):t
螺旋
import turtlet=turtle.Turtle()def drawSpiral(t,lineLen):if lineLen
分形:一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状,即具有自相似的性质
递归可视化:谢尔宾斯基Sierpinski三角形
面积趋于0,周长趋于∞
谢尔宾斯基三角形是由三个尺寸减半的谢尔宾斯基三角形按照品字形拼叠而成
我们无法真正做出谢尔宾斯基三角形,只能做出degree有限的近似图形
在degree有限的情况下,degree=n的三角形,由3个degree=n-1的三角形按品字形拼叠而成,边长均为degree=n的三角形的一半(规模减小)
当degree=0,则就是一个等边三角形,这是递归结束的基本条件
import turtle
def sierpinski(degree,points):colormap=['blue','red','green','white','yellow']
递归的应用:汉诺塔
规则:
一次只能移动一个
大盘子不能叠在小盘子上
假设有5个盘子串在1#柱上,需要移到3#柱上
- 把上面的一摞4个盘子移到2#柱上
- 把剩下的最大号盘子移到3#柱上
- 把2#柱上的4个盘子移到3#柱上
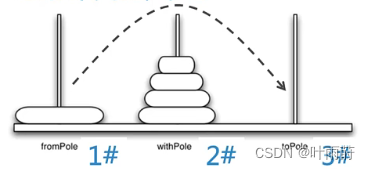
如果能有办法把最上面的4个盘子移到2#柱,那么问题就好解决了。接下来的问题就是把4个盘子从1#移到2#,此时问题规模已经减小:
- 把上面的一摞3个盘子移到3#柱上
- 把剩下的最大号盘子移到2#柱上
- 把3#柱上的3个盘子移到2#柱上
移动3个盘子可以分解为上面2个和下面的最大号盘子
移动2个盘子可以分解为上面的盘子和下面的盘子
思路:一定有三个柱子,两个柱子是无法完成的
将盘子从开始柱,经由中间柱,移到目标柱:
- 将上层N-1个盘子的塔,从开始柱,借助目标柱,移到中间柱;
- 将最大的(第N个)盘子从开始柱移到目标柱;
- 将放置在中间柱的N-1个盘子借助开始柱,移到目标柱
基本结束条件(最小规模问题):1个盘子的移动问题
def moveTower(height,fromPole,withPole,toPole):if height>=1:moveTower(height-1,fromPole,toPole,withPole)moveDisk(height,fromPole,toPole)moveTower(height-1,withPole,fromPole,toPole)
def moveTower(height,fromPole,withPole,toPole):if height>=1:moveTower(height-1,fromPole,toPole,withPole)moveDisk(height,fromPole,toPole)moveTower(height-1,withPole,fromPole,toPole)def moveDisk(disk,fromPole,toPole):print(f"Moving disk[{disk}] from {fromPole} to {toPole}")moveTower(3,"#1","#2","#3")
递归的应用:探索迷宫
将海归放在迷宫中间,找到出口
- 将整个迷宫的空间(矩形)分为行列整齐的方格,区分出墙壁和通道。每个方格具有行列位置,并赋予“墙壁”、“通道”的属性
- 考虑用矩阵方式来实现迷宫数据结构。采用“数据项为字符列表的列表”这两种列表的方式来保存方格内容。采用不同字符分别代表“墙壁+”、“通道 ”、“海归投放点S”,从一个文本文件读入迷宫数据
class Maze:def __init__(self,mazeFileName):rowsInMaze=0columnsInMaze=0self.mazelist=[]mazeFile=open(mazeFileName,'r')rowsInMaze=0for line in mazeFile:rowList=[]col=0for ch in line[:-1]:rowList append(ch)if ch=='S':self.startRow=rowsInMazeself.startCol=colcol=col+1rowsInMaze=rowsInMaze+1self.mazelist.append(rowList)columnsInMaze=len(rowList)
探索迷宫的递归算法思路如下:
- 将海龟
所以需要有个机制记录海龟走过的路径:
沿途洒“面包屑”
递归调用的基本结束条件
def carpet(N,C):def check(n,x,y):if n<=1:return Truen2=n//3if n2<=x<n2*2 and n2<=y<n2*2:return Falsereturn check(n2,x%n2,y%n2)for y in range(N):for x in range(N):if check(N,x,y):print(C,end='')else:print(' '*len(C),end='')print('')
#test
carpet(27,'[]')
分治策略和递归
将问题分为若干更小规模的部分
通过解决每一个小规模部分问题,并将结果汇总得到原问题的解
递归三定律:
基本结束条件,解决最小规模问题
缩小规模,向基本结束条件演进
调用自身来解决已缩小规模的相同问题
❖体现了分治策略
问题解决依赖于若干缩小了规模的问题
汇总得到原问题的解
❖应用相当广泛
排序、查找、遍历、求值等等
优化问题
计算机科学中许多算法都是为了找到某些
问题的最优解
例如,两个点之间的最短路径;
能最好匹配一系列点的直线;
或者满足一定条件的最小集合
兑换最少个数硬币问题
假设你为一家自动售货机厂家编程序,自动售货
机要每次找给顾客最少数量硬币;
假设某次顾客投进$1纸币,买了ȼ37的东西,要
找ȼ63,那么最少数量就是:2个quarter(ȼ25)
、1个dime(ȼ10)和3个penny(ȼ1),一共6个
贪心策略
一般我们这么做:
从最大面值的硬币开始,用尽量多的数量
有余额的,再到下一最大面值的硬币,还用尽量
多的数量,一直到penny(ȼ1)为止
因为我们每次都试图解决问题的尽量大的一部分
对应到兑换硬币问题,就是每次以最多数量的最
大面值硬币来迅速减少找零面值
❖“贪心策略”解决找零兑换问题,在美元
或其他货币的硬币体系下表现尚好
❖动态规划算法采用了一种更有条理的方式
来得到问题的解
❖找零兑换的动态规划算法从最简单的“1
分钱找零”的最优解开始,逐步递加上去
,直到我们需要的找零钱数
❖在找零递加的过程中,设法保持每一分钱
的递加都是最优解,一直加到求解找零钱
数,自然得到最优解
相关文章:

【算法】递归
递归 递归初始递归:数列求和递归的应用:任意进制转换递归深度限制递归可视化:分形树递归可视化:谢尔宾斯基Sierpinski三角形递归的应用:汉诺塔递归的应用:探索迷宫 分治策略和递归优化问题兑换最少个数硬币…...
DC-1靶机刷题记录
靶机下载地址: 链接:https://pan.baidu.com/s/1GX7qOamdNx01622EYUBSow?pwd9nyo 提取码:9nyo 参考答案: https://c3ting.com/archives/kai-qi-vulnhnbshua-tiDC-1.pdf【【基础向】超详解vulnhub靶场DC-1】 https://www.bilibi…...
rust跟我学七:获取外网IP地址
图为RUST吉祥物 大家好,我是get_local_info作者带剑书生,这里用一篇文章讲解get_local_info是怎么获取到本机的外网IP地址。 首先,先要了解get_local_info是什么? get_local_info是一个获取linux系统信息的rust三方库,并提供一些常用功能,目前版本0.2.4。详细介绍地址:[…...

华为:交换机忘记console密码重置
一、背景 许多旧项目经过长时间使用后,因为没有特定的管理运维人员,初始对接人也将初始账号密码等重要信息丢失,现需要进后台查看配置或更改网络配置,需重置密码 二、重置密码,不重置设备方法 1、使用console插入交…...

2024年甘肃省职业院校技能大赛信息安全管理与评估 样题三 模块一
竞赛需要完成三个阶段的任务,分别完成三个模块,总分共计 1000分。三个模块内容和分值分别是: 1.第一阶段:模块一 网络平台搭建与设备安全防护(180 分钟,300 分)。 2.第二阶段:模块二…...

Go 中 slice 的 In 功能实现探索
文章目录 遍历二分查找map key性能总结 之前在知乎看到一个问题:为什么 Golang 没有像 Python 中 in 一样的功能?于是,搜了下这个问题,发现还是有不少人有这样的疑问。 补充:本文写于 2019 年。GO 现在已经支持泛型&am…...
 pyDAL的一些性能优化)
pyDAL一个python的ORM(终) pyDAL的一些性能优化
一、大批量插入数据 对于 大量数据插入时,虽然pyDAL也手册中有个方法:bulk_insert(),但是手册也说了,虽然方法上是一次可以多条数据,如果后端数据库是关系型数据库,他转换为SQL时它是一条一条的插入的&…...

springboot log4j配置xml实例说明
提供样本配置代码 xml <?xml version"1.0" encoding"UTF-8"?> <!--日志级别以及优先级排序: OFF > FATAL > ERROR > WARN > INFO > DEBUG > TRACE > ALL --> <!-- status log4j2内部日志级别 --> <configurat…...
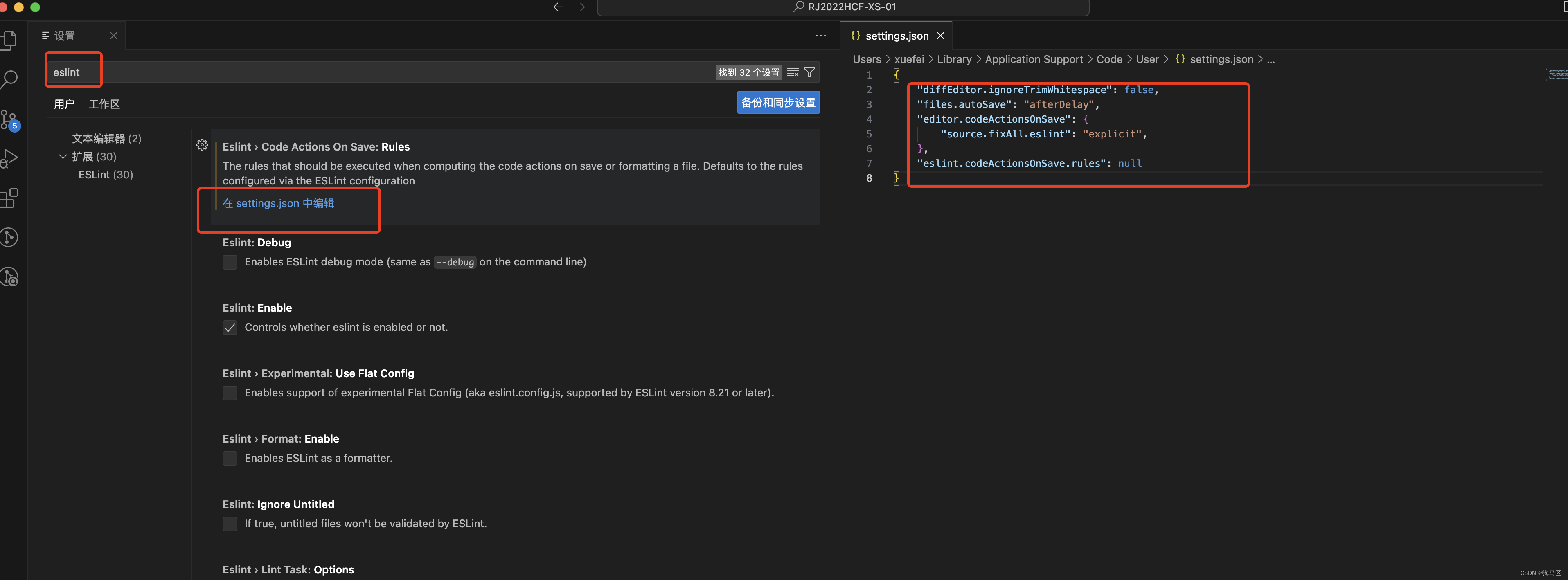
VsCode重新安装需要配机的ESLint和 Prettier - Code formatter 配置
新电脑安装完Vscode后,需要装几个插件,这里记录下: {"diffEditor.ignoreTrimWhitespace": false,"files.autoSave": "afterDelay","editor.codeActionsOnSave": {"source.fixAll.eslint"…...
录屏功能怎么打开?简单操作,一学就会!
录屏功能在当今互联网时代变得越来越重要,无论是游戏录制、在线课程录制还是屏幕操作演示,录屏功能都为我们提供了便捷的解决方案。可是您知道录屏功能怎么打开吗?接下来,让我们一起探索如何在电脑上开启录屏功能,记录…...

小程序显示兼容处理,home键处理
定义: env(safe-area-inset-bottom)和env(safe-area-inset-top)是CSS中的变量,用于获取设备底部和顶部安全区域的大小 示例: padding-bottom: calc(env(safe-area-inset-bottom) 12px); /* 兼容iOS> 11.2 */安全间距类型: …...
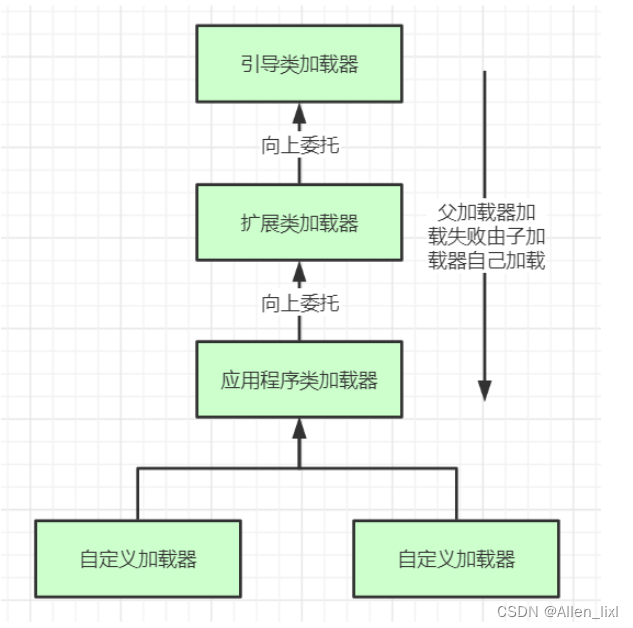
【java八股文】之JVM基础篇
【java八股文】之JVM基础篇-CSDN博客 【java八股文】之MYSQL基础篇-CSDN博客 【java八股文】之Redis基础篇-CSDN博客 【java八股文】之Spring系列篇-CSDN博客 【java八股文】之分布式系列篇-CSDN博客 【java八股文】之多线程篇-CSDN博客 【java八股文】之JVM基础篇-CSDN博…...

2024美赛数学建模思路 - 案例:异常检测
文章目录 赛题思路一、简介 -- 关于异常检测异常检测监督学习 二、异常检测算法2. 箱线图分析3. 基于距离/密度4. 基于划分思想 建模资料 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 一、简介 – 关于异常…...

【EI会议征稿通知】2024年通信技术与软件工程国际学术会议 (CTSE 2024)
2024年通信技术与软件工程国际学术会议 (CTSE 2024) 2024 International Conference on Communication Technology and Software Engineering (CTSE 2024) 2024年通信技术与软件工程国际学术会议 (CTSE 2024)将于2024年03月15-17日在中国长沙举行。会议专注于通信技术与软件工…...

Js面试之作用域与闭包
Js面试之作用域与闭包 作用域词法作用域动态作用域 闭包闭包使用场景封装私有变量模块化开发保持变量状态异步操作 注意事项 最近在整理一些前端面试中经常被问到的问题,分为vue相关、react相关、js相关、react相关等等专题,可持续关注后续内容ÿ…...

Go 爬虫之 colly 从入门到不放弃指南
文章目录 概要介绍如何学习官方文档如何安装快速开始如何配置调试分布式代理层面执行层面存储层面存储多收集器配置优化持久化存储启用异步加快任务执行禁止或限制 KeepAlive 连接扩展总结如果想用 GO 实现爬虫能力,该如何做呢?抽时间研究了 Go 的一款爬虫框架 colly。 概要…...
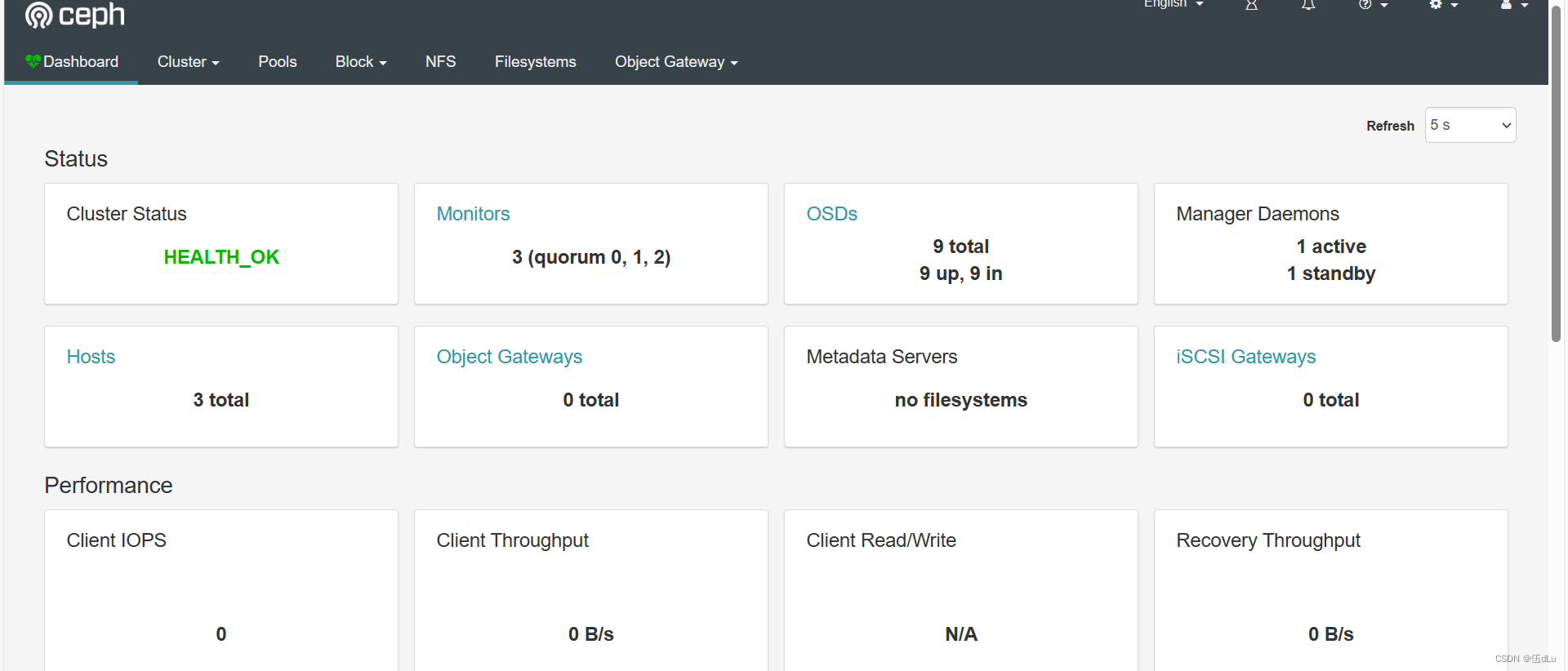
Ceph分布式存储(1)
目录 一.ceph分布式存储 Ceph架构(自上往下) OSD的存储引擎: Ceph的存储过程: 二. 基于 ceph-deploy 部署 Ceph 集群 20-40节点上添加3块硬盘,一个网卡: 10节点为admin,20-40为node&…...

制造业工厂为什么要实施MES系统呢?
MES是生产管理系统,生产管理是通过对生产系统的战略计划、组织、指挥、实施、协调、控制等活动,实现系统的物质变换、产品生产、价值提升的过程。在企业的价值链中,生产经营是企业核心能力的重要组成部分。 实施MES系统的原因 MES系统是中国比…...

Python 一行命令部署http、ftp服务
Python 一行命令部署http服务 文章目录 Python 一行命令部署http服务具体操作命令如下浏览器返回下载Python 一行命令部署FTP服务 具体操作命令如下 这个比nginx相对来说更加简单,可以用于部署特殊场景时如银行等部署时,各种权限控制,内网之间…...

DBA技术栈(三):MySQL 性能影响因素
文章目录 前言一、影响MySQL性能的因素1.1 商业上的需求1.2 应用架构规划1.3 查询语句使用方式1.4 Schema的设计1.5 硬件环境 总结 前言 大部分人都一致认为一个数据库应用系统(这里的数据库应用系统概指所有使用数据库的系统)的性能瓶颈最容易出现在数…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
