【数学】任意一个正整数n最多只有一个质因数大于根号n,怎么证明?
定理
任意一个正整数n最多只有一个大于n\sqrt{n}n的质因子,并且该大于n\sqrt{n}n质因子的幂次是1。
证明(反证法)
证明:最多只有一个大于n\sqrt{n}n的质因子
假设n存在两个大于n\sqrt{n}n的质因子,分别为p1,p2。
已知p1> n\sqrt{n}n,p2> n\sqrt{n}n
所以 p1p2 > (n)2(\sqrt{n})^2(n)2 = n.
又因为 n > p1p2
所以联立得n > p1*p2 > (n)2(\sqrt{n})^2(n)2 = n
即n>n矛盾。所以假设不成立,所以至多有1个大于n\sqrt{n}n的质因子。
证明:该大于n\sqrt{n}n质因子的幂次是1
下面证明如果存在大于n\sqrt{n}n的质因子,该大于n\sqrt{n}n质因子的幂次是1。
假设n存在的1个大于根号n的质因子是p,p的次幂是k>=2(不是1)
已知p> n\sqrt{n}n,k>=2
所以 n >= pkp^kpk >= p2p^2p2 > n
所以n>n矛盾。
所以假设不成立,所以幂次只能是1。
相关文章:

【数学】任意一个正整数n最多只有一个质因数大于根号n,怎么证明?
定理 任意一个正整数n最多只有一个大于n\sqrt{n}n的质因子,并且该大于n\sqrt{n}n质因子的幂次是1。 证明(反证法) 证明:最多只有一个大于n\sqrt{n}n的质因子 假设n存在两个大于n\sqrt{n}n的质因子,分别为p…...

【ES6】var let const 之面试题系列
关于 var、let、const 是前端开发人员经常用到的关键字,也是经典的面试题,接下来就站在面试题的角度来看待它们之间的区别。 一、区别 1. var 声明的范围是函数作用域,let 和 const 声明的范围是块作用域,块作用域是函数作用域的…...
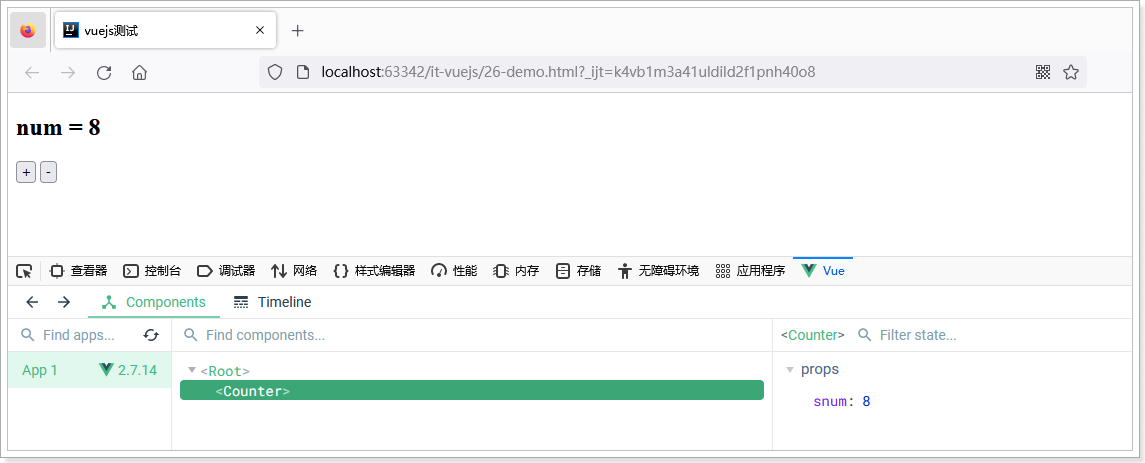
Vue基础入门讲义(四)-组件化
文章目录1.引言2.定义全局组件3.组件的复用4.局部注册5.组件通信5.1.父向子传递props5.2.传递复杂数据5.3.子向父的通信1.引言 在大型应用开发的时候,页面可以划分成很多部分。往往不同的页面,也会有相同的部分。例如可能会有相同的头部导航。 但是如果…...

Android onLayout布局流程解析
组件布局流程结论 1.)layout流程始于ViewRootImpl的performLayout()方法,该方法会调用根View(DecorView)的layout()方法进行布局,因为DecorView是ViewGroup(FrameLayout),所以layout流程来到了ViewGroup(其…...
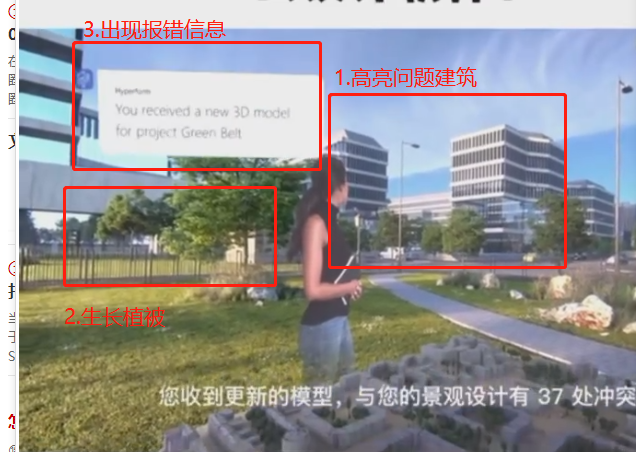
浅分析BIG-建筑展示系统
一、主页(主要界面)重点疑点(需要解决)1.云平台实时同步。是否可以电脑与hololens2同步或链接?并可以传输信息提醒?一级界面(启动界面)1.交互式启动激活效果(触发按钮旋转…...

模电基础(1) 半导体基础知识
基本内容: 1.本征半导体的基本介绍结构; 2.杂质半导体; 3.PN结的形成; 4.PN结的性质。 1.本征半导体 半导体:导电性能介于绝缘体和导体之间的物质。 本征半导体是纯净的晶体结构的半导体。 纯净→无杂质晶体结构→稳…...

阅读笔记:TF - IDF 原理
今天查阅 TF-IDF 资料,发现百度百科里面提供了一个例子,解释的很清楚,记下来备用。 原文链接:https://baike.baidu.com/item/tf-idf/8816134?fraladdin 例子:在某个一共有一千词的网页中 “原子能”、“的” 和 “应…...

【C语言】float 关键字
🚩write in front🚩 🔎大家好,我是謓泽,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎 🏅2021|2022年度博客之星物联网与嵌入式开发TOP5|TOP4…...
)
Linux 网络编程(实现多路IO转接服务器)
1.select函数实现多路IO转接服务器select函数原型:包含在头文件<sys/time.h>,<sys/types.h>和<unistd.h>int select(int nfds, fd_set *readfds, fd_set *writefds,fd_set *exceptfds, struct timeval *timeout);作用:确定…...
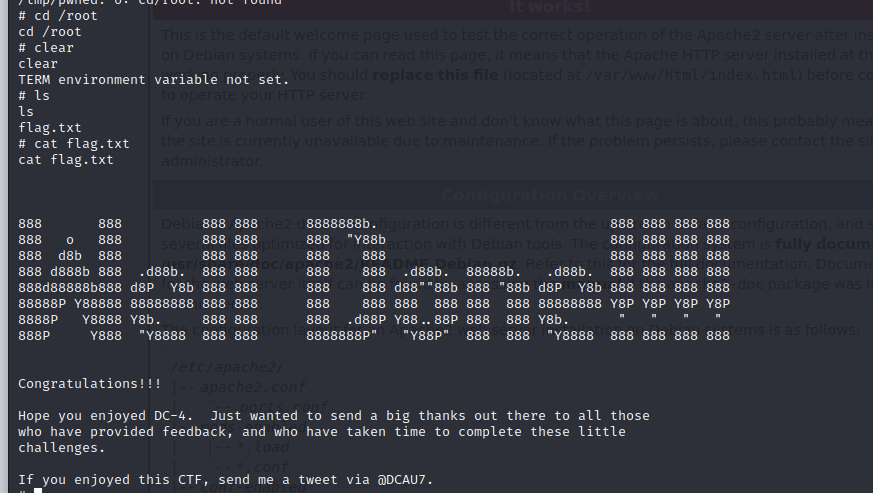
DC-4 靶场学习
信息搜集: 首先获取靶场ip,和之前一样。 arp-scan -l nmap -sP 192.168.28.0/24然后访问。 发现需要登录。 漏洞分析: 直接用bp爆破,爆破出来密码为happy,登录。 发现执行了命令,抓包。 修改命令可以执行ÿ…...
QML组件
一个QML文件定义了一个独立的、顶级的QML组件。 一个QML组件就是一个模板,被QML运行环境解释来创建一个带有一些预定义行为的对象。 一个独立的QML组件可以运行多次来禅城多个对象,每个对象都可以称为该组件的实例。 例子: 在项目中添加一…...

canvas 学习指南
canvas 学习指南 创建一个 canvas <! DOCTYPE html><html xmlns"http://www.w3.org/1999/xhtml"><head><title></title><meta charset"utf-8" /><script type"text/javascript">window.onload fun…...

【华为OD机试2023】开心消消乐 C++
【华为OD机试2023】开心消消乐 C++ 前言 如果您在准备华为的面试,期间有想了解的可以私信我,我会尽可能帮您解答,也可以给您一些建议! 本文解法非最优解(即非性能最优),不能保证通过率。 Tips1:机试为ACM 模式 你的代码需要处理输入输出,input/cin接收输入、print/cou…...

学历?能力?
一个面试官愿意看一张有形的总结报告,还是愿意相信看不到的人品?...
使用ECharts打造一个数据可视化面板
使用ECharts打造一个数据可视化面板1. 使用技术2. 案例适配方案3. 基础设置4. header 布局5. mainbox 主体模块6. 公共面板模块 panel7. 柱形图 bar 模块(布局)8. 中间布局9. ECharts 介绍10. ECharts 体验11. ECharts 基础配置12. 柱状图图表࿰…...

【论文简述】PVSNet: Pixelwise Visibility-Aware Multi-ViewStereo Network(arxiv 2020)
一、论文简述 1. 第一作者:Qingshan Xu 2. 发表年份:2020 3. 发表期刊:arxiv 4. 关键词:MVS、3D重建、可见性、代价体、训练策略 5. 探索动机:ETH3D基准测试提供的图像包含强烈的视图变化,这就要求MVS…...

CSS隐藏元素的几种方式以及display、visibility、opacity的区别
CSS隐藏元素的方式首先最通用且最易想到的方法肯定是display、visibility和opacity这三种了display:none设置元素不可见并且连盒模型也不生成,一般用于不占空间的隐藏元素。display属性规定元素应该生成的框的类型,当其值为“none”时可以规定元素不生成…...

【Java|golang】1487. 保证文件名唯一---golang中string方法的坑
给你一个长度为 n 的字符串数组 names 。你将会在文件系统中创建 n 个文件夹:在第 i 分钟,新建名为 names[i] 的文件夹。 由于两个文件 不能 共享相同的文件名,因此如果新建文件夹使用的文件名已经被占用,系统会以 (k) 的形式为新…...
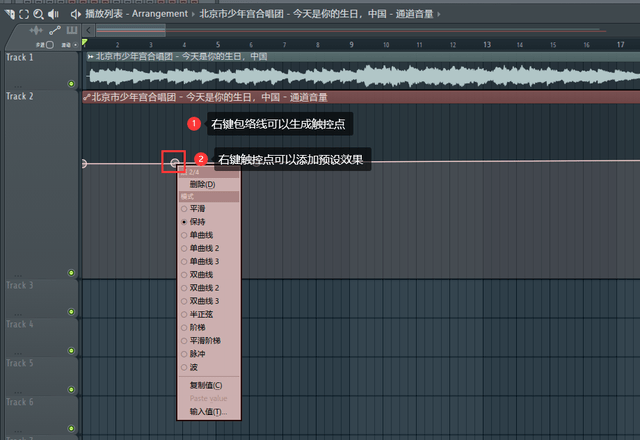
flstudio21水果language选项中文设置方法教程
编曲是通过DAW(数字音频工作站软件)完成的,也就是我们常说的宿主软件。现在有很多优秀的宿主软件,例如Cubase、Studio One、FL Studio等。 FL Studio是一款功能强大的音乐制作软件,也被称为FruityLoops。目前已经推出…...
Ubuntu中安装StaMPS
Ubuntu中安装StaMPS0 StaMPS简介1 首先安装好MATLAB,安装一些依赖工具包2 安装StaMPS2.1 下载StaMPS安装包2.2 安装2.3 配置环境2.4 matlab中的路径设置0 StaMPS简介 官网:https://homepages.see.leeds.ac.uk/~earahoo/stamps/ A software package to e…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...

python打卡day49@浙大疏锦行
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 一、通道注意力模块复习 & CBAM实现 import torch import torch.nn as nnclass CBAM(nn.Module):def __init__…...

【Java】Ajax 技术详解
文章目录 1. Filter 过滤器1.1 Filter 概述1.2 Filter 快速入门开发步骤:1.3 Filter 执行流程1.4 Filter 拦截路径配置1.5 过滤器链2. Listener 监听器2.1 Listener 概述2.2 ServletContextListener3. Ajax 技术3.1 Ajax 概述3.2 Ajax 快速入门服务端实现:客户端实现:4. Axi…...
