CentOS 7安装Java并配置环境
一、安装Java环境
1、检查系统是否安装Java
[root@localhost ~]# java -version2、更新系统软件包
[root@localhost ~]# yum update
#遇到[y/n],选择y并回车,耐心等待下载完毕,之后系统会自动检验更新的软件包
-
遇到 /var/run/yum.pid 已被锁定
/var/run/yum.pid 已被锁定,PID 为 2762 的另一个程序正在运行解决方法-CSDN博客
3、安装Java
[root@localhost ~]# yum install java-1.8.0-openjdk java-1.8.0-openjdk-devel -y
4、验证是否安装成功
[root@localhost ~]# java -version
二、配置Java环境
[root@localhost ~]# vim /etc/profile
#键盘输入"i",在文末插入以下配置信息,Esc :wq 退出并保存
export JAVA_HOME=/usr/lib/jvm/java-1.8.0-openjdk
export PATH=$JAVA_HOME/bin:$PATH
export CLASSPATH=.:$JAVA_HOME/lib/tools.jar:$JAVA_HOME/lib/dt.jar
[root@localhost ~]# source /etc/profile
#使配置环境生效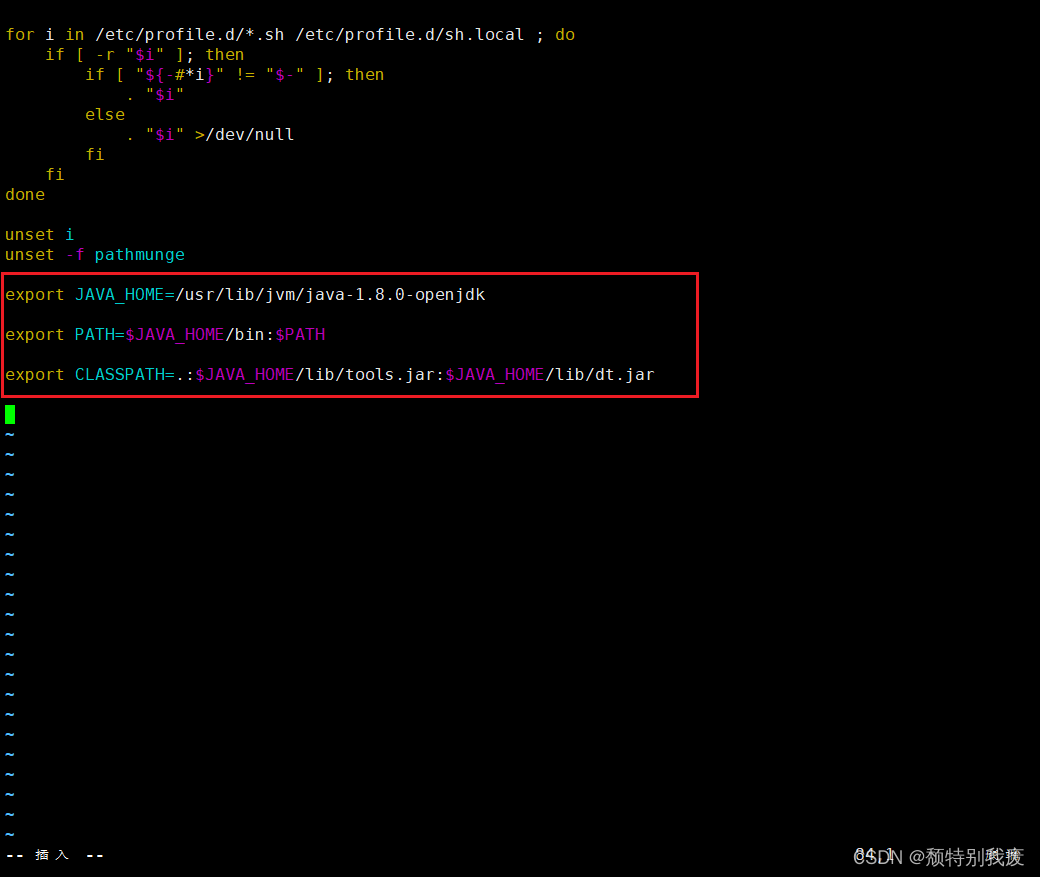
![]()
Java环境安装配置成功
相关文章:

CentOS 7安装Java并配置环境
一、安装Java环境 1、检查系统是否安装Java [rootlocalhost ~]# java -version 2、更新系统软件包 [rootlocalhost ~]# yum update #遇到[y/n],选择y并回车,耐心等待下载完毕,之后系统会自动检验更新的软件包遇到 /var/run/yum.pid 已被锁定 /var/…...
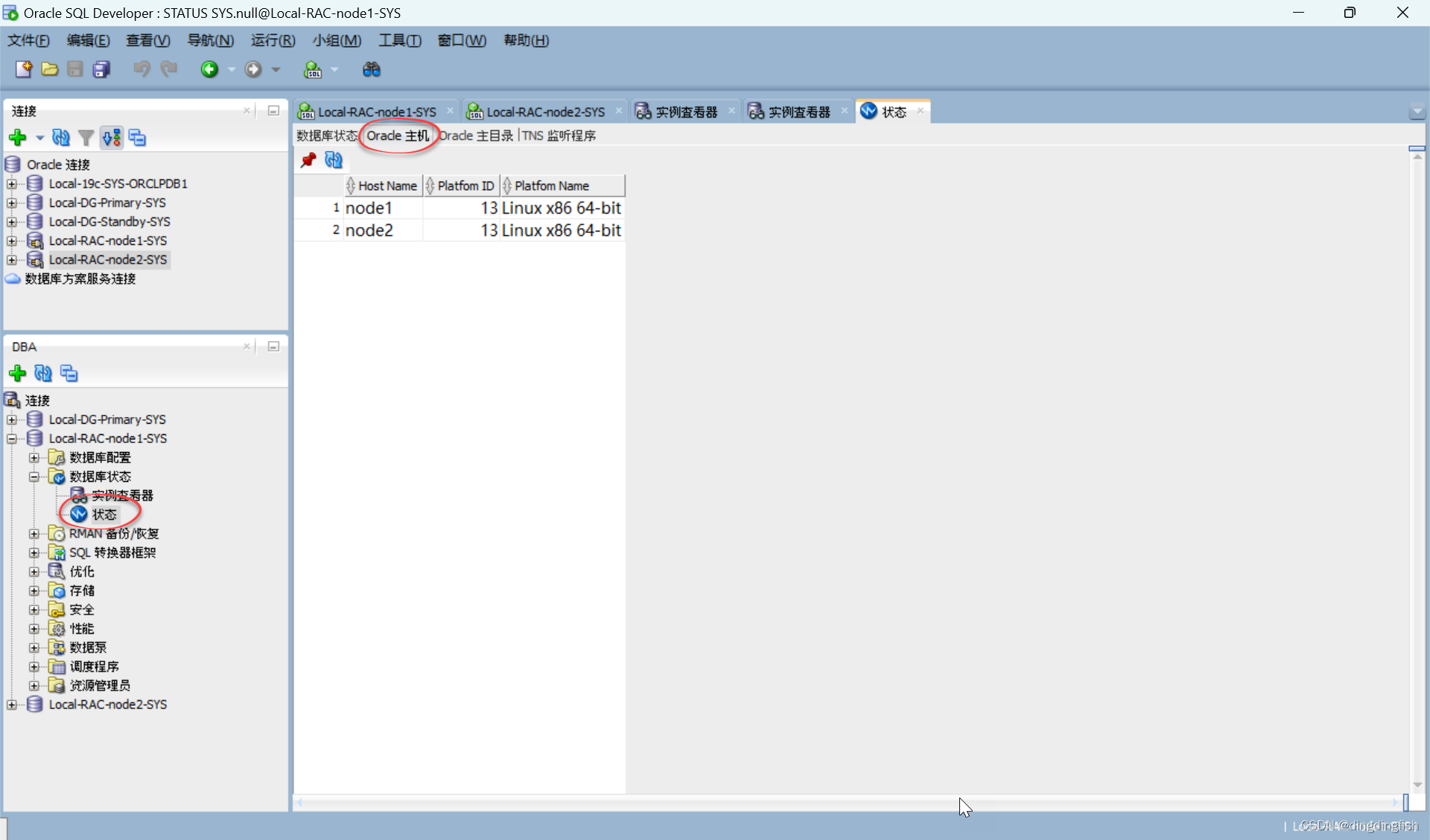
Vagrant创建Oracle RAC环境示例
利用Vagrant安装Oracle RAC(默认为non-CDB模式),生成2台虚机,耗时约1小时。 node1: -----------------------------------------------------------------node1: INFO: 2024-01-11 18:25:54: Make create database commandnode1: …...

鸿蒙 HarmonyOS ArkTS ArkUI 动画 中心缩放、顶部缩放、纵向缩放
EntryComponentstruct Index {State widthA: number 200State heightA: number 200onPageShow():void{animateTo ( {duration: 2000,iterations: -1,curve:Curve.Linear}, () > {this.widthA 0this.heightA 0} )}build() {Column() {// 中心缩放Column(){}.width(this.wi…...

基于python socket实现TCP/UDP通信
两个应用程序如果需要进行通讯最基本的一个前提就是能够唯一的标示一个进程,我们知道IP层的ip地址可以唯一标示主机,而TCP层协议和端口号可以唯一标示主机的一个进程,这样我们可以利用ip地址+协议+端口号唯一标示网络中…...

指针的运算
指针的运算 1.指针-整数 #define N_VALUES 5 float values[N_VALUES]; float* vp; //指针-整数:指针的关系运算 int main() { for (vp &values[0]; vp < &values[N_VALUES];) { *vp 0;//指针每自增一次,就是指向下一个元素的地址 } return …...
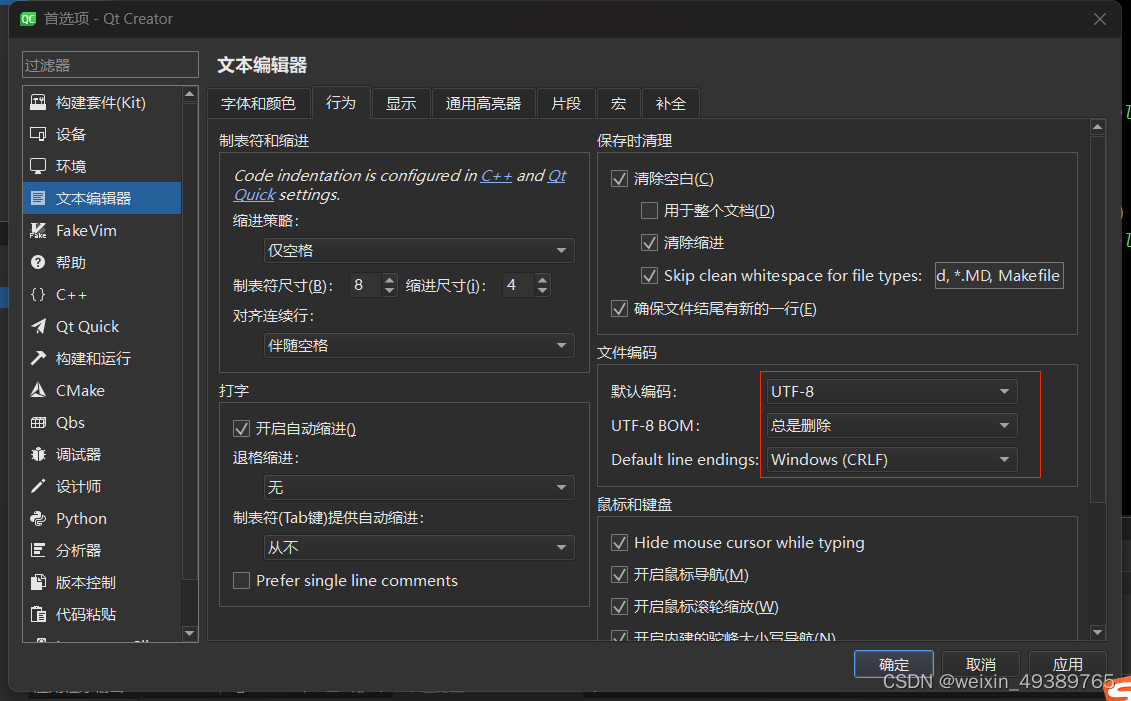
记录一次QT乱码问题
问题描述 在敲陆文周的书《QT5开发及实例》的示例代码时,出现乱码,如下图所示 具体代码如下 Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);ui->treeWidget->clear();int groupSize 2;int ite…...

怎么提升搜狗网站排名
在当今数字化时代,网站排名对于品牌、企业以及个人都至关重要。而对于许多网站来说,搜狗搜索引擎是一个重要的流量来源。为了在搜狗上取得更好的排名,不仅需要优化网站内容,还需要巧妙运用一些工具和技巧。在本文中,我…...
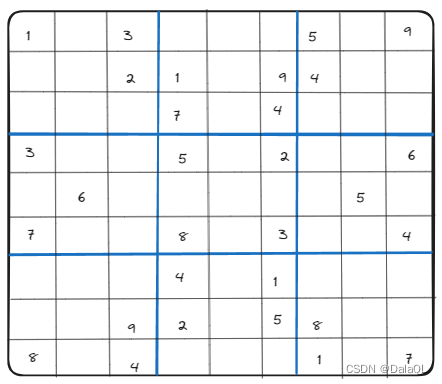
搜索经典题——填充 9*9矩阵
题目:给定一个九行九列矩阵,填充矩阵元素,要求: 1、每一行每一列,每个小九宫格(图片画粗的地方就是)不能包含相同元素 2、每一行,每一列,每个小九宫格均会完整出现1-9的数…...
)
Vue待办事项(组件,模块化)
//html页面代码 <!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title></title> <style> * { padding: 0; margin: 0; }…...
Vue中的组件
在应用程序的开发中,组件是不可缺少的。在Vue的使用中,同样也会用到组件。 vue组件的一般知识点: 1、组件的名字唯一; 2、组件以Html形式书写; 3、组件可以复用; 4、组件可以嵌套&…...
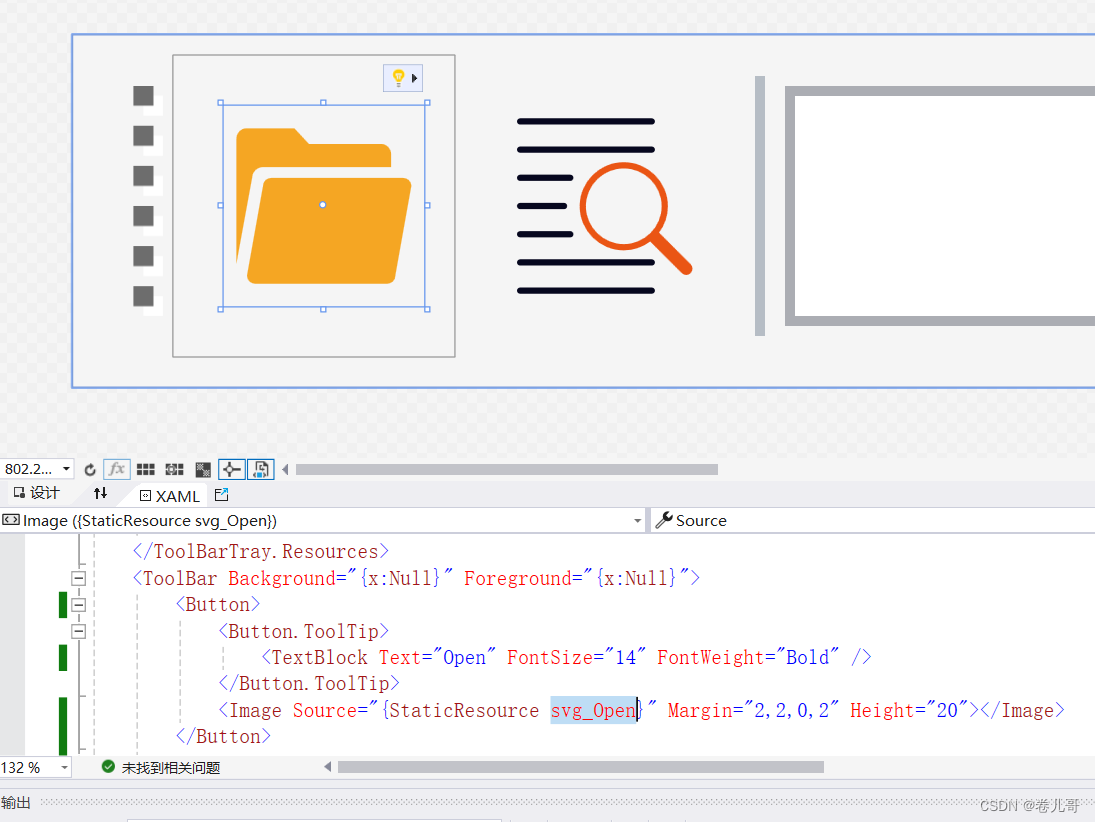
svg矢量图标在wpf中的使用
在wpf应用程序开发中,为支持图标的矢量缩放,及在不同分辨率下界面中图标元素的矢量无损缩放,所以常常用到svg图标,那么如果完 美的将svg图标运用到wpf日常的项目开发中呢,这里分享一下我的个人使用经验和详细步骤。 步…...

如何在云端加速缓存构建
缓存是指将某类数据存储起来以便以后重复使用的过程,它的运用在开发场景中非常普遍。类似于你习惯把最常用的调料放在厨房台面上,而不是橱柜里,这样你在准备大餐时就可以轻松取用。 但对于一个更为技术性、更精确的用例,比如像谷…...
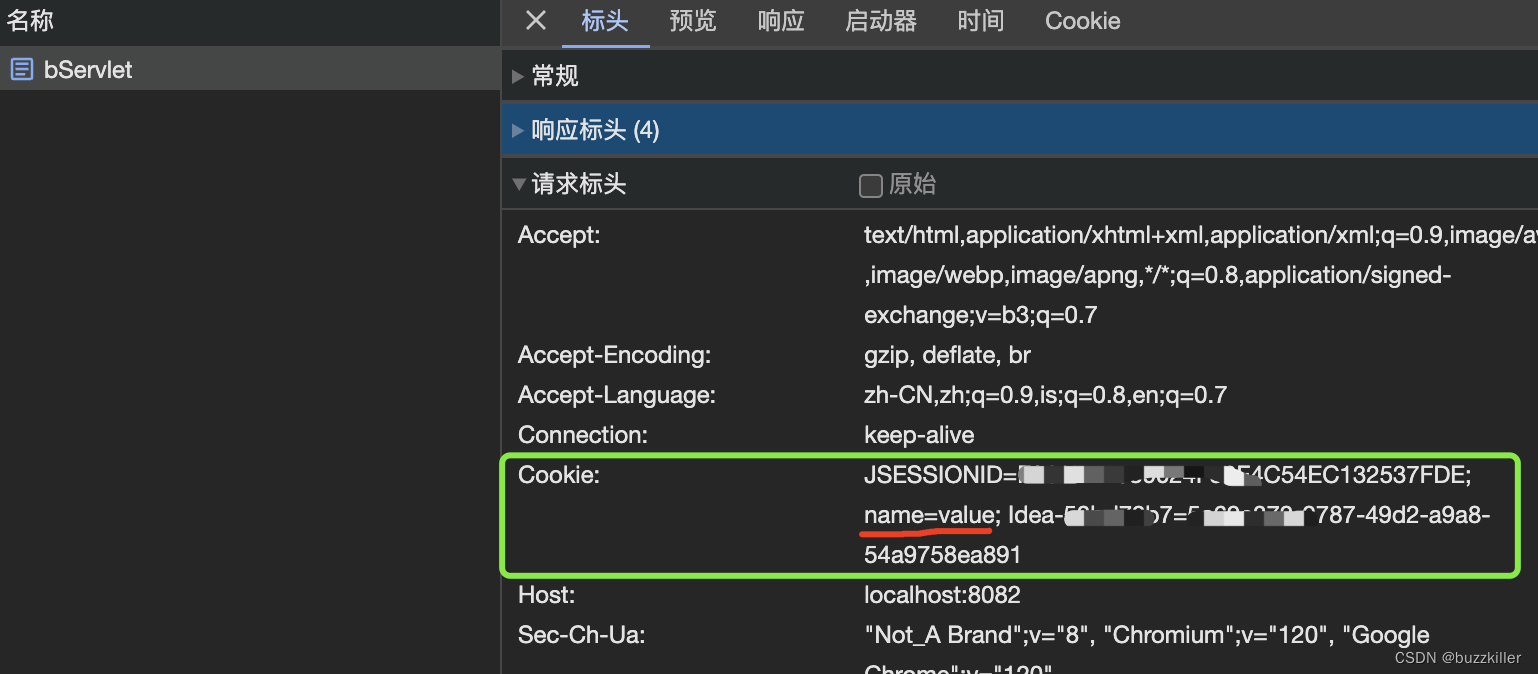
JavaWeb-Cookie与Session
一、概念 是否还记得我们在HTTP概念中提到:HTTP的一大特点是无状态,这意味着多次HTTP请求之间是无法共享数据的。而在请求之间共享一些数据又是我们期望达到的效果。(例如登录的记住我功能)于是便有了会话跟踪技术,而…...
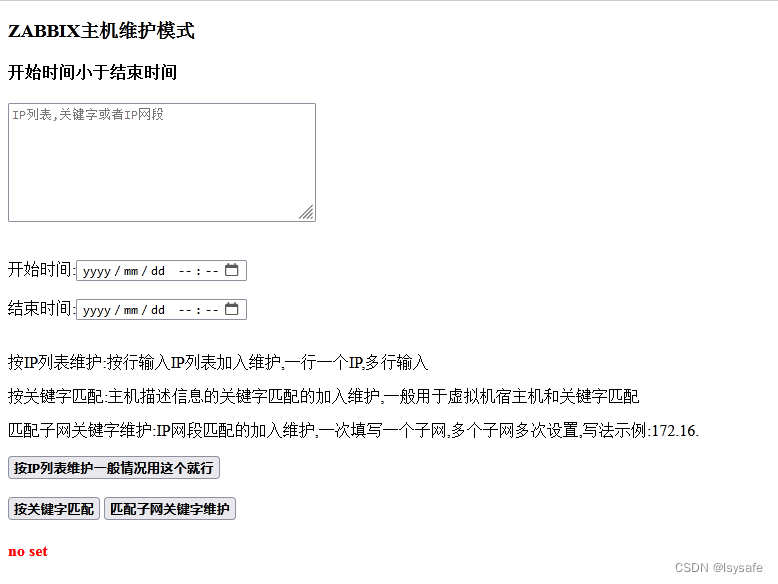
ZABBIX根据IP列表,主机描述,或IP子网批量创建主机的维护任务
有时候被ZABBIX监控的主机可能需要关机重启等维护操作,为了在此期间不触发告警,需要创建主机的维护任务,以免出现误告警 ZABBIX本身有这个API可供调用(不同版本细节略有不同,本次用的ZABBIX6.*),实现批量化建立主机的维护任务 无论哪种方式(IP列表,主机描述,或IP子网)创建维护…...
PMIS_ENT_STD
...

32 登录页组件
效果演示 实现了一个登录页面的样式,包括一个容器、左侧和右侧部分。左侧部分是一个背景图片,右侧部分是一个表单,包括输入框、复选框、按钮和忘记密码链接。整个页面的背景色为白色,容器为一个圆角矩形,表单为一个半透…...

Docker(一)简介和基本概念:什么是 Docker?用它会带来什么样的好处?
作者主页: 正函数的个人主页 文章收录专栏: Docker 欢迎大家点赞 👍 收藏 ⭐ 加关注哦! 一、简介 本章将带领你进入 Docker 的世界。 什么是 Docker? 用它会带来什么样的好处? 好吧,让我们带…...
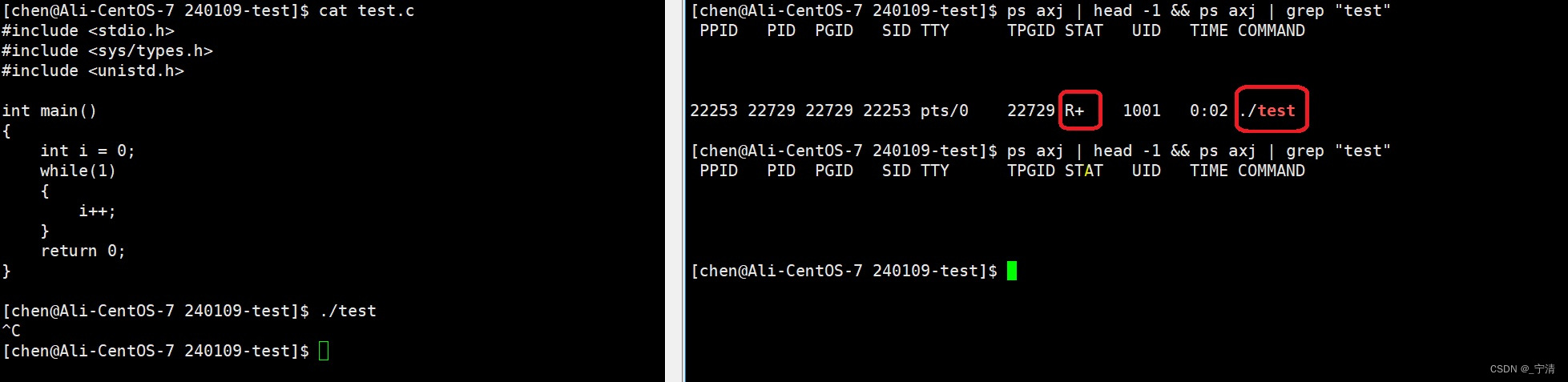
【Linux】进程的概念 进程状态 进程优先级
Content 一、什么是进程1. 进程的概念2. 进程的描述 - 进程控制块(PCB)3. Linux下的进程 二、进程状态1. 教科书中的进程状态运行状态阻塞状态挂起状态 2. Linux下的进程状态R(running)- 运行状态S(sleeping) - 睡眠状…...

Go语言热重载和优雅地关闭程序
Go语言热重载和优雅地关闭程序 我们有时会因不同的目的去关闭服务,一种关闭服务是终止操作系统,一种关闭服务是用来更新配置。 我们希望优雅地关闭服务和通过热重载重新加载配置,而这两种方式可以通过信号包来完成。 1、代码实现 package…...

Python实现两个列表相加的方法汇总
1. 使用 “” 运算符 通过 “” 运算符将两个列表相加,得到一个新的列表。例如: list1 [1, 2, 3] list2 [4, 5, 6] result list1 list2 print(result) # [1, 2, 3, 4, 5, 6]2. 使用 extend 方法 使用 extend 方法将一个列表中的元素逐个添加到另…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
