【算法】DFS与BFS
作者:指针不指南吗
专栏:算法篇🐾题目的模拟很重要!!🐾
文章目录
- 1.区别
- 2.DFS
- 2.1 排列数字
- 2.2 n-皇后问题
- 3.BFS
- 3.1走迷宫
1.区别
| 搜索类型 | 数据结构 | 空间 | 用途 | 过程 |
|---|---|---|---|---|
| DFS | stack | O( n ) | 不能用于最短路 | 搜索到最深处,回溯 |
| BFS | queue | O( n2n^2n2 ) | 可以用于最短路 | 从起点开始,搜索相邻的;再以相邻的位起点,继续 |
这里用两个图来形象的模拟过程
深搜——一条路走到黑

广搜——眼观八方

2.DFS
-
每一个DFS都对应一个搜索树;
-
DFS俗称暴搜,其中有顺序的,经常用到DFS;
-
回溯的时候一定要恢复现场;
-
剪枝就是判断出来当前的方案不合法,不再继续往下深搜,直接回溯;
只说知识,有点抽象,根据两个题来理解一下。
2.1 排列数字
给定一个整数 n,将数字 1∼n 排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数 n。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤7
输入样例:
3输出样例:
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
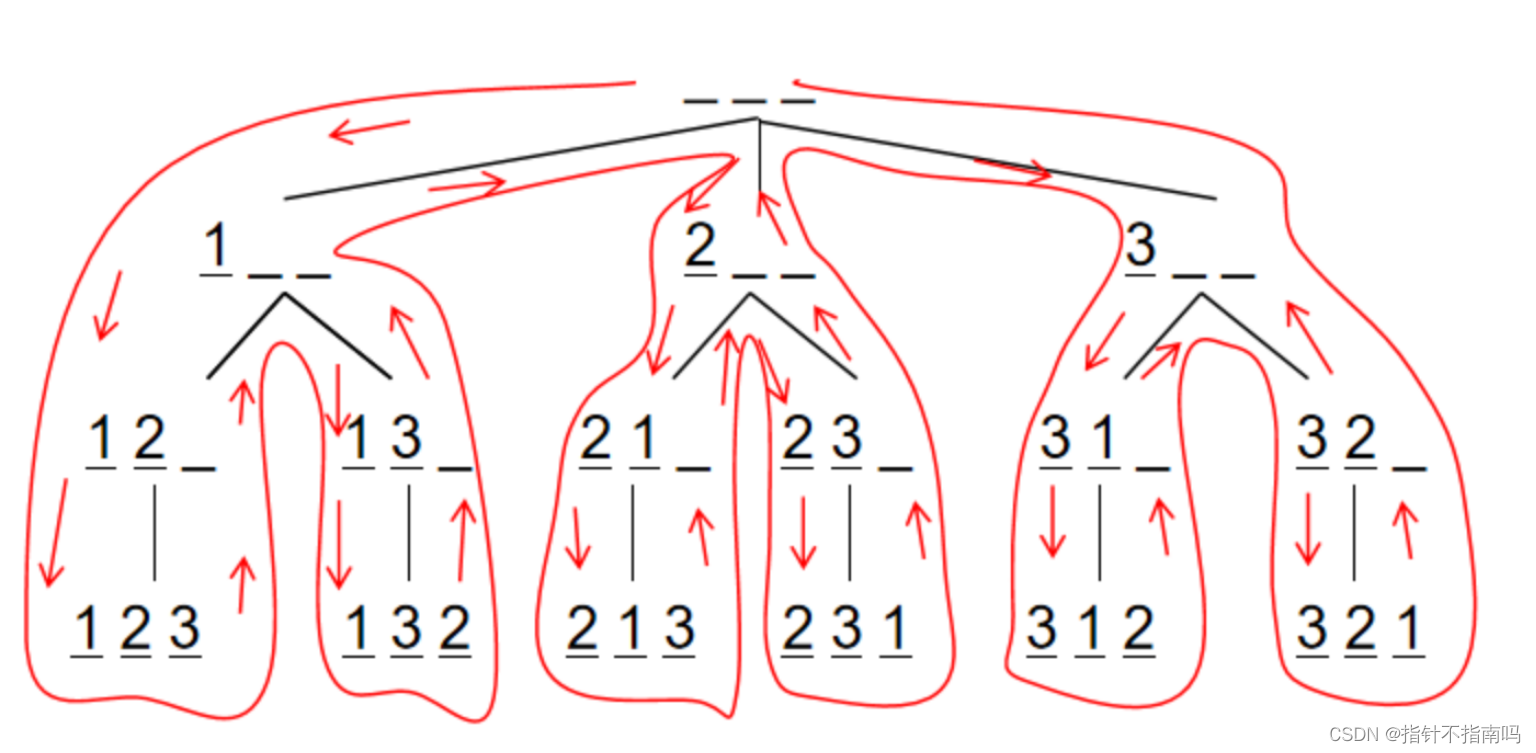
- 思路
图转自acwing以3的全排列为例
-
代码实现
#include<bits/stdc++.h> using namespace std;int n; int path[10];// path 数组保存排列,当排列的长度为 n 时,是一种方案,输出 bool st[10];//st 数组表示数字是否用过:当 st[i] 为 1 时,i 已经被用过,否则 没有被用过void dfs(int u) //dfs(u) 表示:在 path[i] 处填写数字,然后递归的在下一个 u 位置填写数字 {if(u==n){for(int i=0;i<n;i++) cout<<path[i]<<' '; //是一种方案输出cout<<endl;return ;}for(int i=1;i<=n;i++){if(!st[i]) //i 没有被使用过,现在使用{st[i]=true; //状态 改成使用过path[u]=i; //在方案中填上这个数dfs(u+1); //填下一个位置上的数st[i]=false; //回溯:第 i 个位置填写某个数字的所有情况都遍历后, 第 i 个位置填写下一个数字}} }int main() {cin>>n;dfs(0); //从第0个位置上,开始递归,搜索return 0; }
2.2 n-皇后问题
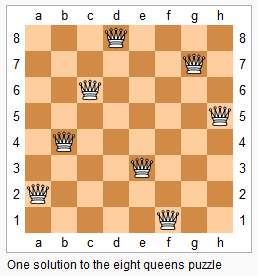
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中
.表示某一个位置的方格状态为空,Q表示某一个位置的方格上摆着皇后。每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4输出样例:
.Q.. ...Q Q... ..Q...Q. Q... ...Q .Q..
方法一
-
思路
棋盘皇后这个题,和数的全排列很相似
按行枚举,枚举的时候,就保证了行不会重复;
开始放置棋子,第
u行第i列 看看是否可以放皇后,可以就放,递归下一行u+1直到最后,全部 n 个皇后放上棋盘
图解如下
图转自acwing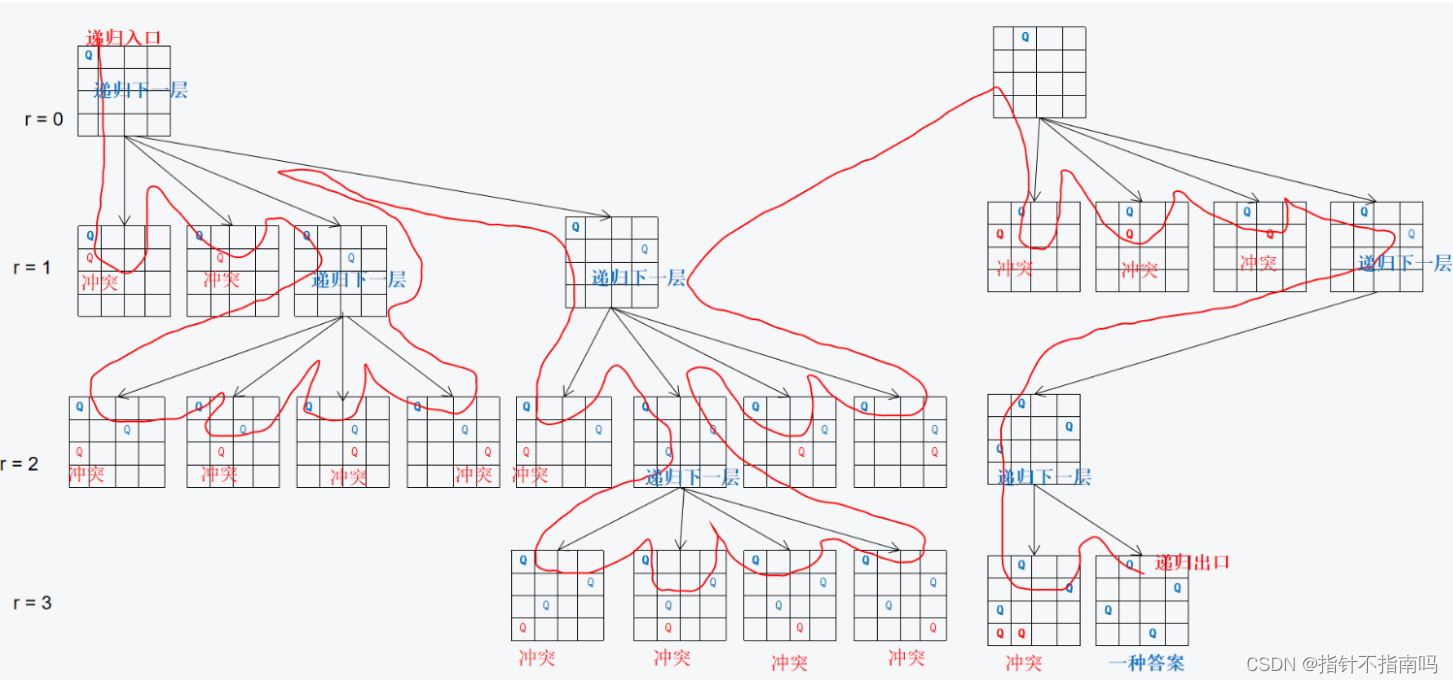
-
代码实现
#include<bits/stdc++.h> using namespace std;int n; const int N=20; char q[N][N]; //存储棋盘 bool cor[N],dg[2*N],udg[2*N]; //cor表示每一列,dg和udg表示正对角线和反对角线,来存储他们的是否被使用过的状态 void dfs(int u) //放第 u 行的棋子 (深度优先遍历) {if(u==n) //如果放盘,则输出棋盘{for(int i=0;i<n;i++){for(int j=0;j<n;j++)cout<<q[i][j];cout<<endl;}cout<<endl;return ; //重点!! 递归到最深层,返回,千万别忘记}for(int i=0;i<n;i++) //从第一列,开始遍历,是否放棋{if(!col[i]&&!dg[i+u]&&!udg[n-i+u]) //如果 列,对角线,没有被放过,则放皇后{q[u][i]='Q'; //放上col[i]=dg[i+u]=udg[n-i+u]=true; //改变状态,dg[i+u]表示截距,每个对角线,都有自己独有的截距;反对角线的截距是负数,数组的下标,不能存放负数,所以加上 n这个偏移量dfs(u+1); //放下一行的col[i]=dg[i+u]=udg[n-i+u]=false; //恢复现场q[u][i]='.';}} }int main() {cin>>n;for(int i=0;i<n;i++)for(int j=0;j<n;j++)q[i][j]='.'; //初始化棋盘dfs(0); //从第0行,开始放棋子return 0; }
方法二
-
思路
枚举 每一个位置的棋子
每个位置可以分成两种情况:放
Q不放Q把每一种情况都枚举出来
-
代码实现
#include<bits/stdc++.h> using namespace std;int n; const int N=20; char q[N][N]; bool row[N], col[N],dg[N],udg[N];void dfs(int x,int y,int s) //x表示行,y表示列,s表示已经放上皇后的个数 {//处理超边界地情况if(y==n) y=0,x++; if(x==n) //每个位置都枚举完了{if(s==n) // n 个皇后都放上去了{for(int i=0;i<n;i++)puts(q[i]); //输出棋盘, q[i],传的是数组指针,输出的是一整行puts("");}return ; //递归到最后返回}//分支1,不放皇后dfs(x,y+1,s);//分支2,放皇后if(!row[x]&&!col[y]&&!dg[x+y]&&!udg[n-x+y]){q[x][y]='Q';row[x]=col[y]=dg[x+y]=udg[n-x+y]=true;dfs(x,y+1,s+1);row[x]=col[y]=dg[x+y]=udg[n-x+y]=false;q[x][y]='.';}}int main() {cin>>n;for(int i=0;i<n;i++)for(int j=0;j<n;j++)q[i][j]='.';dfs(0,0,0);return 0; }
3.BFS
比较简单,一般模板可以直接解决
直接上例题,来理解一下
3.1走迷宫
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 00 或 11,其中 00 表示可以走的路,11 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1)处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m) 处,至少需要移动多少次。
数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
5 5 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0输出样例:
8
-
思路
从起点开始,遍历每一个位置,
看他四个方向,是否满足条件,满足条件的,走它,
在看它的四个方向是否满足条件,满足走它
每走一步,距离+1,
最后返回 走到 终点 的距离
图解如下
图转自acwing
-
代码实现
#include<bits/stdc++.h> using namespace std;typedef pair<int ,int> PII; //定义 坐标const int N=110;int n,m; int g[N][N]; //表示地图 int d[N][N]; //存的是某一点到源点的距离int dfs() {queue<PII> q; //定义队列,里面存的表示我们将要走的哪一个点q.push({0,0}); //先把放进去,表示我们要走 起点memset(d,-1,sizeof d); //初始化,把每个点到源点的距离初始化为 -1d[0][0]=0; //源点到自己的距离为0int dx[4]={0,0,-1,1},dy[4]={1,-1,0,0}; //我们定义的四个方向 x,y 的移动,这样可以避免 4个判断语句,注意 dx,dy 要一一对应//从第一个开始位置开始遍历while(!q.empty()) //走到最后{auto t=q.front(); //把队列中的第一个元素取出来q.pop(); //对头元素出列for(int i=0;i<4;i++){int x=t.first+dx[i],y=t.second+dy[i]; //扩展之后的坐标//x,y不能越界,可以走,没走过if(x>=0&&x<n&&y>=0&&y<m&&g[t.first][t.second]==0&&d[x][y]==-1){d[x][y]=d[t.first][t.second]+1; //距离+1q.push({x,y}); //把把满足条件地坐标插进去,下一次走它们}}}return d[n-1][m-1]; //返回最后一个即终点到源点地距离 }int main() {cin>>n>>m;for(int i=0;i<n;i++)for(int j=0;j<m;j++)cin>>g[i][j]; //读入地图cout<<dfs()<<endl;return 0; }

相关文章:

【算法】DFS与BFS
作者:指针不指南吗 专栏:算法篇 🐾题目的模拟很重要!!🐾 文章目录1.区别2.DFS2.1 排列数字2.2 n-皇后问题3.BFS3.1走迷宫1.区别 搜索类型数据结构空间用途过程DFSstackO( n )不能用于最短路搜索到最深处&a…...

湖州银行冲刺A股上市:计划募资约24亿元,资产质量水平较高
3月4日,湖州银行股份有限公司(下称“湖州银行”)递交招股书,准备在上海证券交易所主板上市。本次冲刺上市,湖州银行计划募资23.98亿元,将在扣除发行费用后全部用于补充该行资本金。 湖州银行在招股书中表示…...
高性能网络I/O框架-netmap源码分析
前几天听一个朋友提到这个netmap,看了它的介绍和设计,确实是个好东西。其设计思想与业界不谋而合——因为为了提高性能,几个性能瓶颈放在那里,解决方法自然也是类似的。 netmap的出现,它既实现了一个高性能的网络I/O框…...
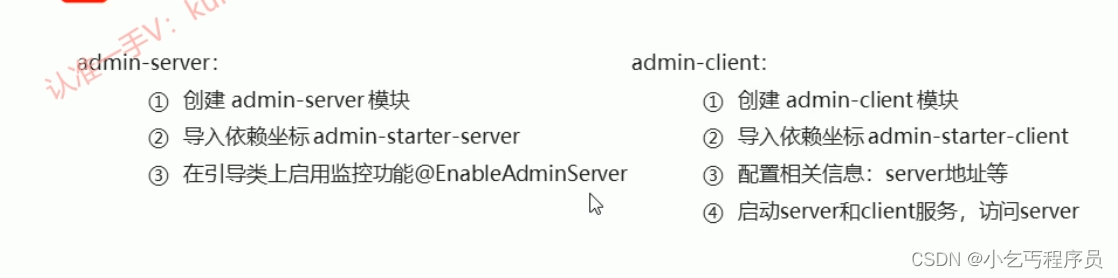
SpringBoot监听机制-以及使用
11-SpringBoot事件监听 Java中的事件监听机制定义了以下几个角色: ①事件:Event,继承 java.util.EventObject 类的对象 ②事件源:Source ,任意对象Object ③监听器:Listener,实现 java.util…...
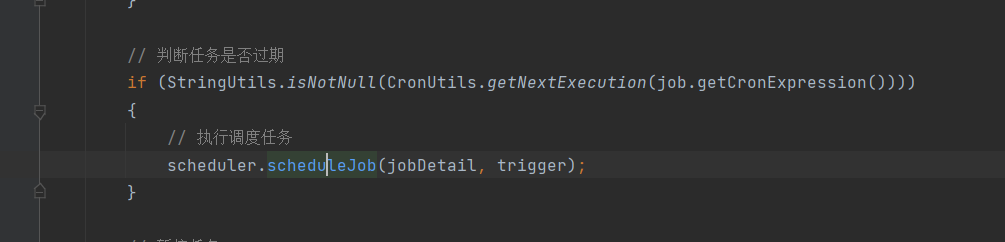
若依学习——定时任务代码逻辑 详细梳理(springboot整合Quartz)
springboot整合Quartz关于若依定时任务的使用可以去看视频默认定时任务的使用关于springboot整合quartz的整合参考(150条消息) 定时任务框架Quartz-(一)Quartz入门与Demo搭建_quarzt_是Guava不是瓜娃的博客-CSDN博客(150条消息) SpringBoot整合Quartz_springboot quartz_桐花思…...
)
C++---最长上升子序列模型---拦截导弹(每日一道算法2023.3.4)
注意事项: 本题为"线性dp—最长上升子序列的长度"的扩展题,这里只讲贪心思路,dp去这个看。 题目: 某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。 但是这种导弹拦截系统有一个缺陷:虽然它…...

【机器学习面试】百面机器学习笔记和问题总结+扩展面试题
第1章 特征工程 1、为什么需要对数值类型的特征做归一化? (1)消除量纲,将所有特征统一到一个大致相同的区间范围,使不同指标之间具由可比性; (2)可以加快梯度下降收敛的速度&#…...
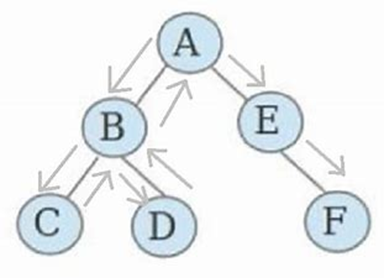
【2021.12.28】ctf逆向中的迷宫问题(含exe及wp)
【2021.12.28】ctf逆向中的迷宫问题(含exe及wp) 文章目录【2021.12.28】ctf逆向中的迷宫问题(含exe及wp)1、迷宫简介(1)简单例子(2)一般的迷宫代码2、二维迷宫(1…...
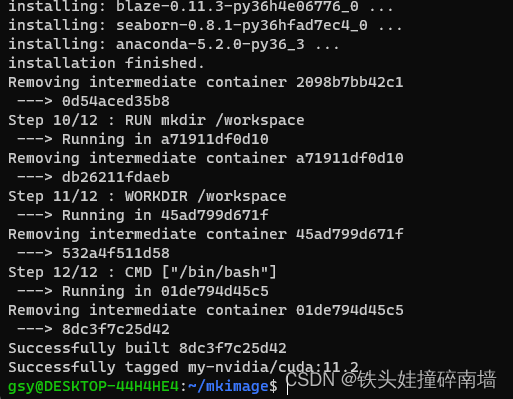
WSL2使用Nvidia-Docker实现深度学习环境自由部署
1. Win11 显卡驱动的安装 注意:WSL2中是不需要且不能安装任何显卡驱动的,它的显卡驱动完全依赖于 Win11 中的显卡驱动,因此我们只需要安装你显卡对应的 Win11 版本显卡驱动版本(必须是 Win11 版本的驱动),…...
SpringBoot入门 - 配置热部署devtools工具
在SpringBoot开发调试中,如果我每行代码的修改都需要重启启动再调试,可能比较费时间;SpringBoot团队针对此问题提供了spring-boot-devtools(简称devtools)插件,它试图提升开发调试的效率。准备知识点什么是…...

CANFDNET-200U-UDP配置与数据收发控制
一、启动ZCANPRP,打开设备管理页面,选择类型CANFDNET-200U-UDP,如图1 图1 二、打开设备,启动,在相应页面如图2,配置协议,CANFD 加速,本地端口,IP地址,工作端口。 图2 三、发送相应数…...
嵌入式中backtrace的使用
大家好,我是bug菌~ backtrace主要用于调试程序时,能够打印出程序在运行过程中的函数调用栈,以帮助开发者快速定位程序出现异常或崩溃的原因。 通过backtrace的输出,开发者可以了解程序在哪个函数出现问题,…...
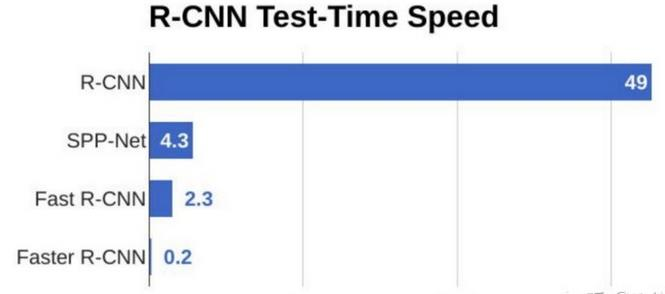
CV学习笔记-Faster-RCNN
Faster R-CNN 文章目录Faster R-CNN1. 目标检测算法1.1 计算机视觉有五大应用1.2 目标检测任务1.3 目标检测算法概述2. 边框回归(Bounding-Box regression)2.1 IoU2.2 统计学中的指标2.3 边框回归3. Faster-RCNN网络3.1 Conv layers3.2 Region Proposal …...
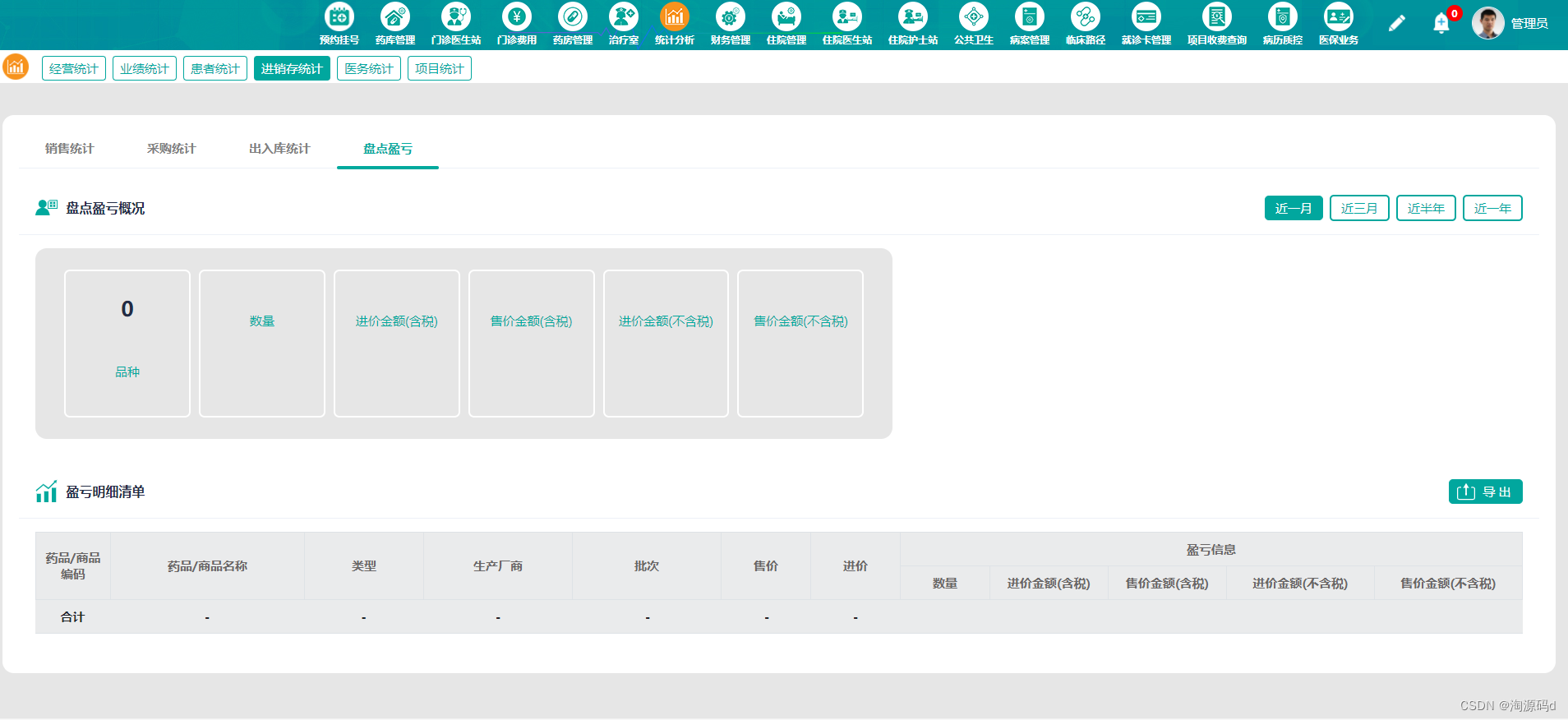
大型三甲医院云HIS系统源码 强大的电子病历+完整文档
医院HIS系统源码云HIS系统:SaaS运维平台多医院入驻强大的电子病历完整文档 有源码,有演示 一、系统概述 采用主流成熟技术,软件结构简洁、代码规范易阅读,SaaS应用,全浏览器访问前后端分离,多服务协同&am…...

如何使用Spring Cloud搭建高可用的Elasticsearch集群?详解Elasticsearch的安装与配置及Spring Boot集成的实现
Spring Cloud 是一个基于 Spring Boot 的微服务框架,它提供了一系列组件和工具,方便开发人员快速搭建和管理分布式系统。Elasticsearch 是一个开源的全文搜索引擎,也是一个分布式、高可用的 NoSQL 数据库。本篇博客将详细讲解如何使用 Spring…...
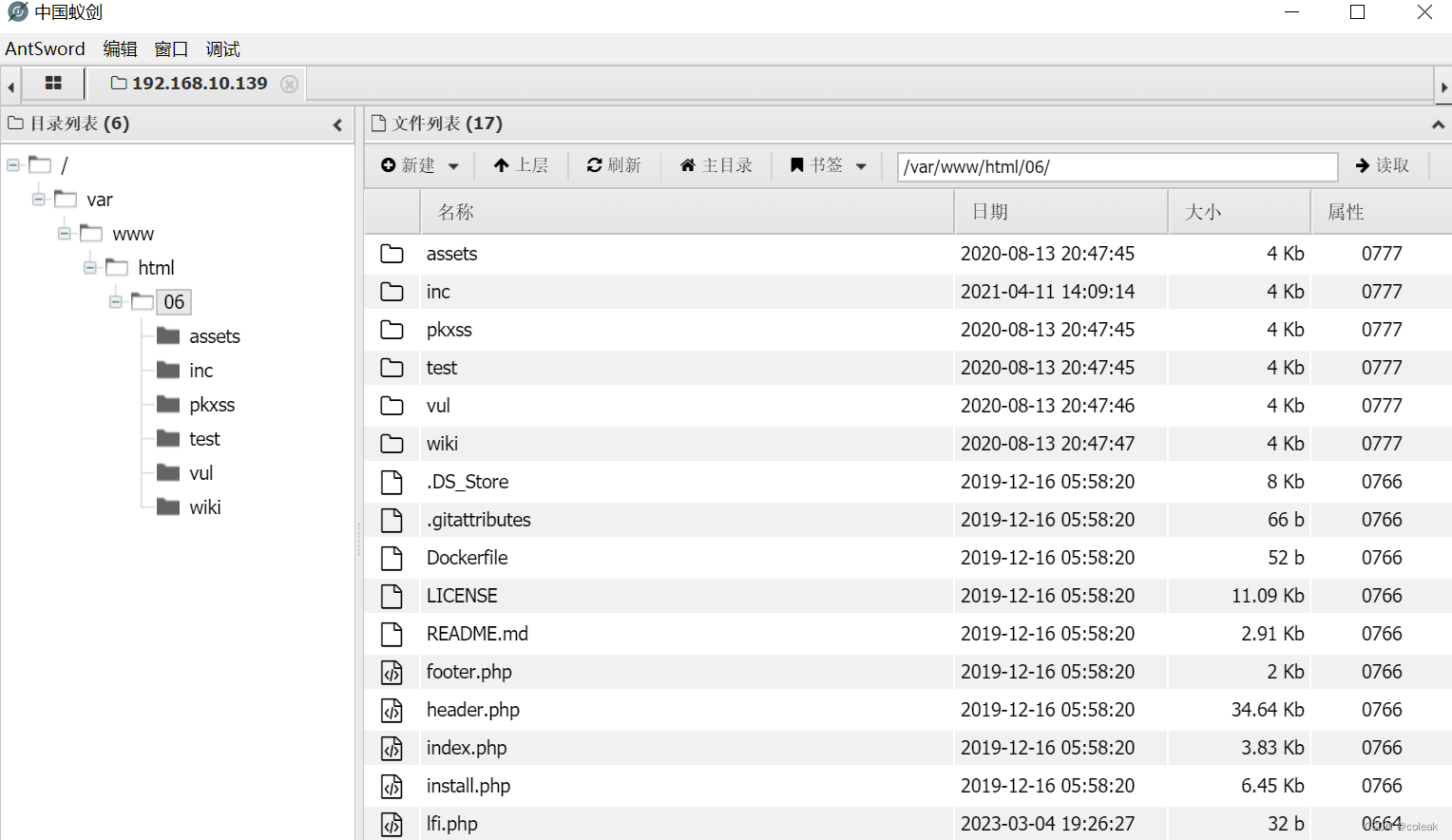
phpinfo包含临时文件Getshell全过程及源码
目录 前言 原理 漏洞复现 靶场环境 源码 复现过程 前言 PHP LFI本地文件包含漏洞主要是包含本地服务器上存储的一些文件,例如session文件、日志文件、临时文件等。但是,只有我们能够控制包含的文件存储我们的恶意代码才能拿到服务器权限。假如在服…...

ubuntu22.04 Desktop 服务器安装
操作系统 使用的是Uubntu22.04 Desktop的版本,系统安装后,默认开启了53端口和631端口 关闭udp 5353、53791端口(avahi-daemon服务) sudo systemctl stop avahi-daemon.socket avahi-daemon.service sudo systemctl disable ava…...

Halcon——关于halcon中的一些语法
Halcon——关于halcon中的一些语法前言一、变量的创建与赋值二、if语句三、for语句四、while语句五、中断语句六、switch语句总结前言 在HDevelep环境下编程时,所用的一些语法与C#有些差异,在此做下记录。 一、变量的创建与赋值 Hdevelep中调用函数时&…...

Java 循环语句
Java 循环语句 循环语句就是在满足一定条件的情况下反复执行某一个操作的语句。Java中提供了3种常用的循环语句,分别是while循环语句、do…while循环语句和for循环语句。 1.while循环语句 while语句也称条件判断语句,它的循环方式为利用一个条件来控制…...

Python 基础语法
文章目录条件判断循环数据类型变量字符编码字符串格式化listtupledictset不可变对象”#“ 开头的是注释每一行是一个语句,当语句以冒号 “:” 结尾时,缩进的语句被视为代码块 好处:强迫代码格式化,强迫少用缩进 坏处:“…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...