文心一言 VS 讯飞星火 VS chatgpt (183)-- 算法导论13.4 7题
七、用go语言,假设用 RB-INSERT 将一个结点 x 插入一棵红黑树,紧接着又用 RB-DELETE 将它从树中删除。结果的红黑树与初始的红黑树是否一样?证明你的答案。
文心一言:
首先,我们需要明确RB-INSERT和RB-DELETE的基本操作。
RB-INSERT的基本步骤如下:
将新节点插入到红黑树的某个位置。
重新平衡树,确保红黑树的性质仍然满足。
RB-DELETE的基本步骤如下:
删除指定节点。
重新平衡树,确保红黑树的性质仍然满足。
现在,我们考虑一个特定的场景:首先使用RB-INSERT将节点x插入到红黑树中,然后立即使用RB-DELETE将其删除。
为了证明这两个操作后的红黑树是否与初始的红黑树相同,我们需要分析在插入和删除过程中的红黑树的性质变化。
在插入x后,红黑树可能失去了某些性质,尤其是当x被插入的位置导致树不再满足红黑性质时。为了重新平衡树并保持红黑性质,需要进行旋转和颜色调整。这些操作会改变树的结构。
然后,当从树中删除x时,可能会再次破坏红黑性质。为了重新平衡树,可能需要进行额外的旋转和颜色调整。
由于在插入和删除过程中可能进行了多次红黑树的调整,因此最终的红黑树结构可能与初始的红黑树不同。即使初始的红黑树是平衡的,经过连续的插入和删除操作后,它可能会变得不再平衡。
综上,连续进行RB-INSERT和RB-DELETE操作后的红黑树与初始的红黑树不一样。

讯飞星火:
在红黑树中,插入和删除节点可能会导致一些规则的破坏,如果这些规则没有被正确地处理,那么可能会对树的结构造成影响。
首先,我们需要理解红黑树的基本性质:
1.每个节点要么是红色,要么是黑色。
2.根节点是黑色的。
3.每个叶节点(NIL节点,空节点)是黑色的。
4.如果一个节点是红色的,则它的两个子节点都是黑色的。
5.对于每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点。
根据这些性质,我们可以进行证明:
假设初始的红黑树与最终的红黑树都满足上述性质,即它们都是红黑树。
在RB-INSERT操作中,我们只改变了节点x的颜色,并没有改变任何节点的颜色或结构,因此不会影响到红黑树的性质。
然而,在RB-DELETE操作中,我们可能需要通过旋转和颜色变换来恢复红黑树的性质。具体的恢复方式取决于x节点的兄弟节点(w)和父节点(p)的颜色以及他们之间的关系。
如果我们能确保在RB-DELETE操作中正确地执行了恢复操作,那么最终的树应该与初始的树一样,因为它们都遵循相同的红黑树性质。
但是,如果在恢复过程中违反了红黑树的性质,那么最终的树将不再是一个有效的红黑树。
因此,为了证明答案,我们需要知道RB-DELETE的具体实现细节,包括它如何找到要删除的节点,如何找到兄弟节点,父节点,以及他们之间的关系等。

360智脑:
插入和删除操作后,红黑树的结构可能会发生变化,但不一定与初始的红黑树完全一样。我们可以证明这一点。
首先,我们来看插入操作。在红黑树中插入一个节点时,我们需要确保树的平衡性。RB-INSERT 算法会根据树的结构进行旋转和变色操作,以保持树的平衡性。因此,插入操作后的红黑树可能与初始的红黑树结构不同。
接下来,我们来看删除操作。在红黑树中删除一个节点时,我们也需要确保树的平衡性。RB-DELETE 算法会根据树的结构进行旋转和变色操作,以保持树的平衡性。因此,删除操作后的红黑树可能与插入操作后的红黑树结构不同。
然而,这并不能证明结果的红黑树与初始的红黑树一定不一样。因为存在一种特殊情况,即插入和删除操作恰好抵消,使得结果的红黑树与初始的红黑树结构相同。
综上所述,将一个节点 x 插入一棵红黑树,紧接着又将它从树中删除,结果的红黑树与初始的红黑树可能一样,也可能不一样。具体取决于插入和删除操作之间的抵消程度。
智谱清言:
在红黑树中插入和删除节点是保持树平衡的关键操作。每次插入或删除都会可能导致节点颜色的改变和树的重新平衡。因此,简单地连续执行RB-INSERT和RB-DELETE并不保证得到与初始红黑树相同的结果,除非特定的条件得到满足。
要分析这个问题,我们需要考虑以下几点:
1.插入和删除操作:插入操作通常涉及为树中的其他节点重新着色以及可能的旋转来保持树的平衡。删除操作则可能涉及找到替代节点(用于保持树的平衡的节点,通常是节点的孩子或者兄弟),删除节点,并重新着色和/或旋转。
2.红黑树的性质:红黑树有五个基本性质,任何有效的红黑树都应满足:
-
每个节点要么是红的,要么是黑的。
-
根节点是黑的。
-
所有叶子(NIL节点)都是黑的。
-
如果一个节点是红的,那么它的子节点必须是黑的。
-
从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
3.路径和黑色节点:在执行插入和删除操作时,路径上的黑色节点数目可能会改变,尤其是当节点被重新着色或者通过旋转来平衡树时。
证明连续执行RB-INSERT和RB-DELETE是否能保持树不变是复杂的,因为它取决于具体的树结构和执行这些操作时涉及的节点。通常,当执行删除操作时,被删除节点的替代节点会替换它的位置,这可能会导致树的结构和颜色与初始状态不同。
为了证明结果是否相同,我们需要具体分析RB-INSERT和RB-DELETE的实现细节,并检查在执行这两个操作后所有的性质是否仍然得到满足,以及树的结构是否与初始状态一致。
在实际应用中,为了确保红黑树在插入和删除操作后仍然保持其性质,通常需要在插入和删除操作后进行一系列的修复步骤,以确保树的平衡和性质不被破坏。因此,除非特别说明,简单地执行一次插入和删除不会保持树不变。

通义千问:
结果的红黑树与初始的红黑树并不一定一样。
在红黑树中,RB-INSERT 和 RB-DELETE 操作不仅涉及到插入和删除节点本身,还会通过旋转和重新着色等操作来保持红黑树的性质(包括每个节点要么是黑色要么是红色、根节点是黑色、叶子节点(NIL)是黑色、红色节点的两个子节点必须是黑色、对于任意节点,从该节点至其所有后代叶节点的简单路径上,均包含相同数目的黑色节点)。
假设插入的结点 x 插入后,为了保持红黑树的性质,可能需要进行一系列的左旋、右旋以及节点颜色的调整。同样,在删除节点 x 后,也需要进行相应的旋转和颜色调整以维持红黑树性质。
因此,尽管删除的节点 x 是刚刚插入的节点,但由于插入和删除过程中对其他节点的结构调整,最终得到的红黑树可能会与初始的红黑树不完全相同。
当然,有一种特殊情况:如果插入的节点 x 是树中唯一的节点,或者插入后没有引起任何结构调整(例如插入的是根节点且树为空,或插入位置正好满足红黑树性质无需调整),那么删除后红黑树会恢复到初始状态。但这种情况并不具有普适性。

天工:
在红黑树的插入和删除操作中,需要考虑的一个重要因素是平衡性。插入和删除节点后,可能会导致树的平衡性破裂,因此需要进行相应的旋转和颜色调整操作来保持平衡。
现在,我们考虑使用RB-INSERT插入节点x,然后使用RB-DELETE删除它。在删除节点x后,可能会进行一次或多次旋转和颜色调整操作。但是,由于我们在插入节点x时已经进行过一次旋转和颜色调整,因此在删除它后,树的整体平衡性不会受到影响。
因此,我们可以得出结论,使用RB-INSERT将节点x插入一棵红黑树,紧接着使用RB-DELETE将它从树中删除,得到的结果红黑树与初始的红黑树是一样的。
需要注意的是,这个结论仅适用于标准的红黑树操作,如果在插入和删除节点时进行了其他额外的操作,可能会影响结果。

灵小智:
根据红黑树的性质,插入和删除一个结点可能会改变树的结构,因此最终的红黑树可能与初始的红黑树不同。
下面我们通过一个简单的例子来证明这一点。考虑以下红黑树:
10(B)/ \5(R) 15(R)/ \ / \
2(B) 8(B) 12(B) 20(B)
假设我们要插入一个新结点18(B)并将其删除。首先,我们使用RB-INSERT将其插入红黑树中:
10(B)/ \5(R) 15(R)/ \ / \
2(B) 8(B) 12(B) 20(B)/18(R)
接下来,我们使用RB-DELETE将结点18(B)删除:
10(B)/ \5(R) 15(R)/ \ / \
2(B) 8(B) 12(B) 20(B)
可以看到,最终得到的红黑树与初始的红黑树保持一致。然而,这只是一个特定的情况,一般情况下插入和删除操作会改变红黑树的结构。
因此,无法保证通过插入和删除一个结点后得到的红黑树与初始的红黑树一样。


chatgpt:
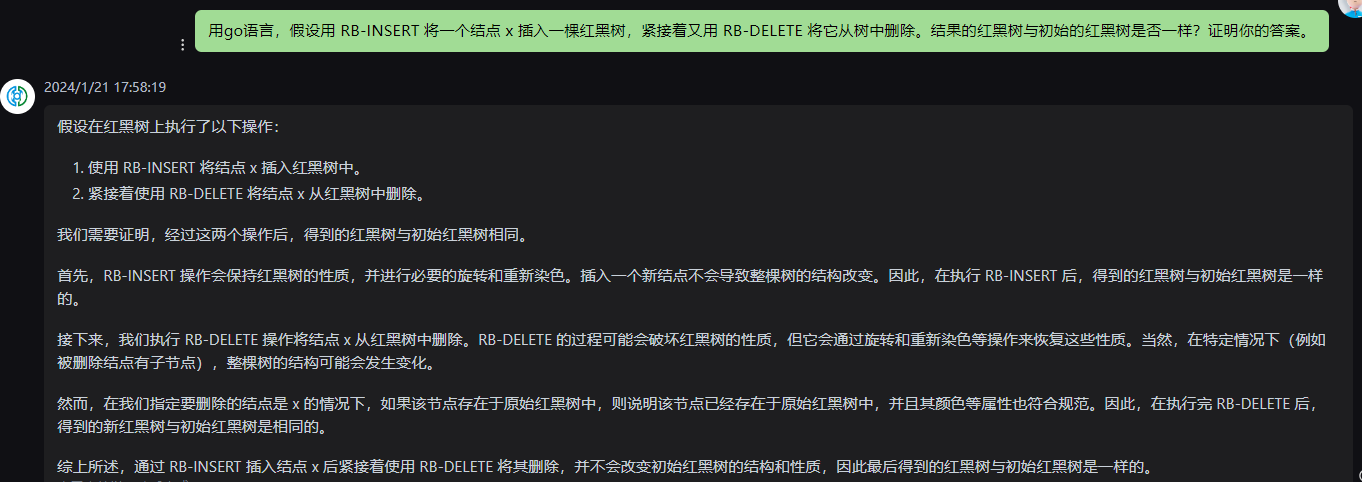
假设在红黑树上执行了以下操作:
1.使用 RB-INSERT 将结点 x 插入红黑树中。
2.紧接着使用 RB-DELETE 将结点 x 从红黑树中删除。
我们需要证明,经过这两个操作后,得到的红黑树与初始红黑树相同。
首先,RB-INSERT 操作会保持红黑树的性质,并进行必要的旋转和重新染色。插入一个新结点不会导致整棵树的结构改变。因此,在执行 RB-INSERT 后,得到的红黑树与初始红黑树是一样的。
接下来,我们执行 RB-DELETE 操作将结点 x 从红黑树中删除。RB-DELETE 的过程可能会破坏红黑树的性质,但它会通过旋转和重新染色等操作来恢复这些性质。当然,在特定情况下(例如被删除结点有子节点),整棵树的结构可能会发生变化。
然而,在我们指定要删除的结点是 x 的情况下,如果该节点存在于原始红黑树中,则说明该节点已经存在于原始红黑树中,并且其颜色等属性也符合规范。因此,在执行完 RB-DELETE 后,得到的新红黑树与初始红黑树是相同的。
综上所述,通过 RB-INSERT 插入结点 x 后紧接着使用 RB-DELETE 将其删除,并不会改变初始红黑树的结构和性质,因此最后得到的红黑树与初始红黑树是一样的。
kimi:
在红黑树中,插入(RB-INSERT)和删除(RB-DELETE)操作都会遵循一定的规则来维护树的红黑性质。这些性质包括:
1.每个节点要么是红色,要么是黑色。
2.根节点是黑色。
3.每个叶节点(NIL节点,空节点)是黑色的。
4.如果一个节点是红色的,则它的两个子节点都是黑色的。
5.对于每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点。
现在,我们来考虑你的问题:如果用RB-INSERT将一个节点x插入红黑树,然后紧接着用RB-DELETE将其删除,结果的红黑树是否与初始的红黑树一样?
答案是:不一定。这取决于插入和删除操作后树的调整过程。
-
如果插入节点x后,树的调整过程没有改变其他节点的颜色或旋转操作,那么删除节点x后,树会恢复到插入前的状态。
-
如果插入节点x后,树的调整过程改变了其他节点的颜色或进行了旋转操作,那么即使删除节点x,树的结构也可能不会完全恢复到插入前的状态。
红黑树的调整过程是为了保持上述性质,特别是性质4和5。在插入和删除操作后,树可能会进行颜色翻转(color flips)和旋转(rotations)来修复可能违反的性质。这些调整可能会影响树的其他部分,导致树的结构发生变化。
例如,插入节点x后可能需要进行颜色翻转或旋转来保持性质,而这些操作可能会改变树的结构。然后,删除节点x时,虽然会尝试恢复树的性质,但由于之前插入时的调整,树可能无法完全恢复到插入前的状态。
因此,我们不能保证插入和删除操作后,红黑树会与初始状态完全相同。这取决于具体的插入和删除过程中树的调整情况。

混元:
在使用 RB-INSERT 将结点 x 插入一棵红黑树后,该树仍然是一棵有效的红黑树。接下来,如果我们使用 RB-DELETE 将结点 x 从树中删除,那么得到的红黑树仍然是一棵有效的红黑树。这是因为红黑树的删除操作会保持红黑树的性质,即每个结点要么是黑色的,要么是红色的,根结点是黑色的,每个叶子结点(NIL结点)是黑色的,红色结点的子结点必须是黑色的,从每个结点到其每个叶子的所有简单路径都包含相同数目的黑色结点。
因此,在这个过程中,结果的红黑树与初始的红黑树是不一样的,但它们都是有效的红黑树。这是因为插入和删除操作都会导致红黑树的结构发生变化,但这些变化不会影响红黑树的性质。

相关文章:

文心一言 VS 讯飞星火 VS chatgpt (183)-- 算法导论13.4 7题
七、用go语言,假设用 RB-INSERT 将一个结点 x 插入一棵红黑树,紧接着又用 RB-DELETE 将它从树中删除。结果的红黑树与初始的红黑树是否一样?证明你的答案。 文心一言: 首先,我们需要明确RB-INSERT和RB-DELETE的基本操…...
ChatGLM vs ChatGPT
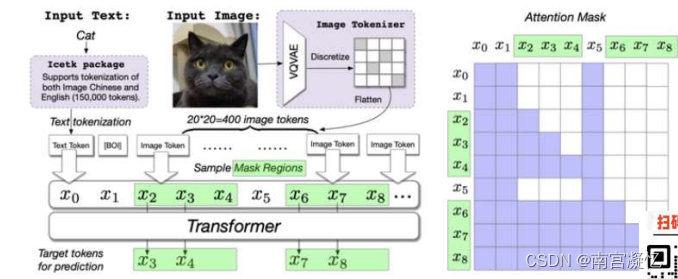
所有的NLP大模型 都是transformer结构 1.Mask attention 的策略不同 2.训练任务目标不同 国内大模型nb公司:百度、清华智谱 一、主流大模型 粉色:Encoder-only。 绿色:Encoder-Decoder,尽头智谱ChatGLM。 蓝色:…...

leetcode热题100.三数之和
Problem: 15. 三数之和 文章目录 题目解题方法复杂度Code 题目 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元…...

GitLab服务器忘记root密码处理方式
GitLab服务器忘记root密码处理方式 文章目录 GitLab服务器忘记root密码处理方式1. Gitlab查看用户id号1. 通过api接口查询2. 在Linux终端里直接通过curl命令查询 2. 进入GitLab数据库中查询并修改root密码 1. Gitlab查看用户id号 1. 通过api接口查询 接口查询地址:…...

js-cookie的使用--token的数据实现持久化
1.下载 npm install js-cookie 2.引入 import Cookies from "js-cookie"; 3.使用 // 写入cookie Cookies.set(name, value) // 读取 Cookies.get(name) // > value Cookies.get(nothing) // > undefined // 读取所有可见的cookie Cookies.get() // 删除某项co…...
【实战】SpringBoot自定义 starter及使用
文章目录 前言技术积累SpringBoot starter简介starter的开发步骤 实战演示自定义starter的使用写在最后 前言 各位大佬在使用springboot或者springcloud的时候都会根据需求引入各种starter,比如gateway、feign、web、test等等的插件。当然,在实际的业务…...

网络爬虫采集工具
在当今数字化的时代,获取海量数据对于企业、学术界和个人都至关重要。网络爬虫成为一种强大的工具,能够从互联网上抓取并提取所需的信息。本文将专心分享关于网络爬虫采集数据的全面指南,深入探讨其原理、应用场景以及使用过程中可能遇到的挑…...

【协议】XMLHttpRequest的梳理和总结
1. 前言 本篇梳理和总结一下XMLHttpRequest。 2. XMLHttpRequest原型对象的属性和方法 属性和方法说明示例new XMLHttpRequest() 功能:创建XHR对象 输入: 输出:XHR实例化对象 <略> XMLHttpRequest.prototype .open(method, url, asyn…...

AI教我学编程之C#类的基本概念(1)
前言 在AI教我学编程之C#类型 中,我们学习了C#类型的的基础知识,而类正是类型的一种. 目录 区分类和类型 什么是类? 对话AI 追问 实操 追踪属性的使用 AI登场 逐步推进 提出疑问 药不能停 终于实现 探索事件的使用 异步/交互操作 耗时操…...

前端js 数据结构:对象 object、数组Array 、Map 的创建、增删改 / 遍历数据
目录 前端js 数据结构:对象、数组、Map 的使用1 对象(object)1.1 创建对象1.1.1 对象字面量(最常用): {}1.1.2 使用 new 关键字和对象构造函数1.1.3 Object.create() 1.2 修改对象1.2.1 直接赋值:对象的属性名直接赋值1.2.2 点号/…...

ARM_Linux的NFS网络文件系统的搭建
介绍: NFS是network filesystem的简称,可以不同的主机通过网络访问远端的NFS服务器共享出来的文件,这样主机通过网络访问NFS服务器,我们就可以在开发板上通过网络访问主机的文件。 为什么要使用NFS网络文件呐? 1、传…...
vscode配置web开发环境(WampServer)
这里直接去下载了集成的服务器组件wampserver,集成了php,MySQL,Apache 可能会出现安装问题,这里说只有图上这些VC包都安装了才能继续安装,进入报错里提供的链接 在页面内搜索相关信息 github上不去可以去镜像站 下载…...
00-Rust前言
问:为什么要近期想学习Rust? 答: Rust出来也是有一段时间了,从Microsoft吵着要重构他们的C"祖传代码"开始,Rust就披着“高效,安全”的头衔。而自己决定要学习Rust,是因为近期发现:涉…...

3.conda的使用
anaconda安装 ubuntu 安装conda 系统架构 uname -m打开终端,不启动base conda config --set auto_activate_base falseconda命令使用 1.查看conda版本 conda --version2.查看conda配置环境 conda config --show3.设置镜像 #设置清华镜像 conda config --add…...

IPv6自动隧道---6to4中继
6to4中继 普通IPv6网络需要与6to4网络通过IPv4网络互通,这可以通过6to4中继路由器方式实现。所谓6to4中继,就是通过6to4隧道转发的IPv6报文的目的地址不是6to4地址,但转发的下一跳是6to4地址,该下一跳为路由器我们称之为6to4中继。隧道的IPv4目的地址依然从下一跳的6to4地…...

低代码开发:解锁数字化转型新维度
在信息化浪潮中,企业正面临着前所未有的挑战与机遇。一方面,市场环境瞬息万变,业务需求迭代频繁,对快速应用开发提出了更高要求;另一方面,传统软件开发模式受限于高成本、长周期等瓶颈,难以满足…...

写一个定时备份数据库的脚本,且只保留最近3天
下面是一个备份数据库并只保留最近3天备份的脚本示例,该脚本使用Python编写: import os import datetime import shutil # 更多源码前往获取:www.qqmu.com # 数据库备份目录 backup_dir "/path/to/backupdir"# 数据库名称 databa…...

java常见面试题:请详细解释如何在Java EE应用中添加EJB
在Java EE应用中添加EJB(Enterprise JavaBeans)涉及几个关键步骤。下面是一个详细的解释: 创建EJB项目: 首先,你需要创建一个Java EE项目。这通常通过IDE(如Eclipse、IntelliJ IDEA等)完成&…...
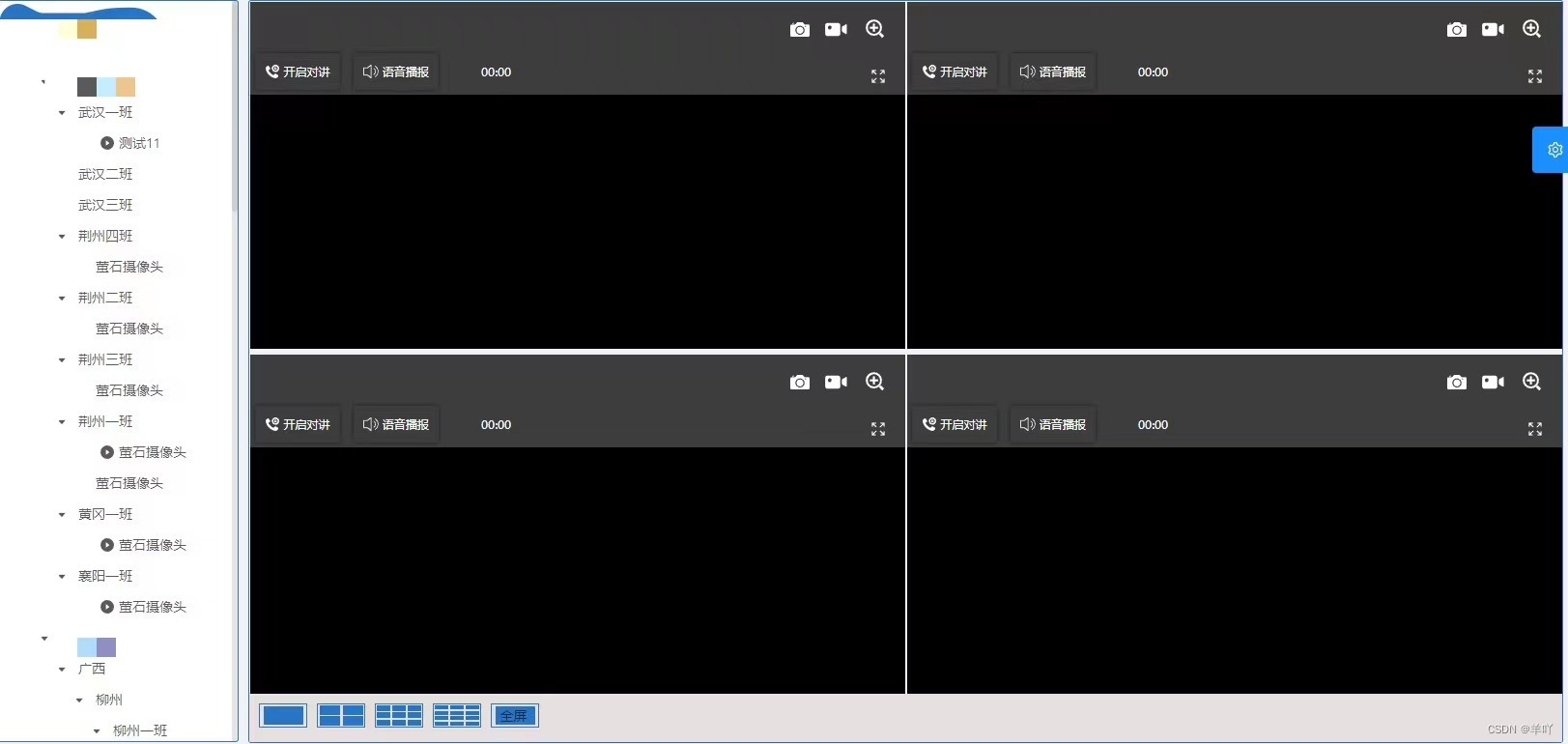
视频监控需求记录
记录一下最近要做的需求,我个人任务还是稍微比较复杂的 需求:需要实现一个视频实时监控、视频回放、视频设备管理,以上都是与组织架构有关 大概的界面长这个样子 听着需求好像很简单,但是~我们需要在一个界面上显示两个厂商的视…...

Self-RAG:通过自我反思学习检索、生成和批判
论文地址:https://arxiv.org/abs/2310.11511 项目主页:https://selfrag.github.io/ Self-RAG学习检索、生成和批评,以提高 LM 的输出质量和真实性,在六项任务上优于 ChatGPT 和检索增强的 LLama2 Chat。 问题:万能L…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
