算法常用思路总结
思路
- 1. 求数组中最大最小值
- 思路
- 代码
- 2. 计算阶乘
- 思路:
- 代码:
- 3. 得到数字的每一位
- 思路
- 代码
- 4. 计算时间类型
- 5. 最大公约数、最小公倍数
- 6. 循环数组的思想
- 题目:猴子选大王
- 代码
- 补充
- 经典例题
- 1. 复试四则运算
- 题目内容
- 题解
- 2. 数列求和
- 题目内容
- 题解
1. 求数组中最大最小值
思路
把数组中下标为0的值,先设置为最大(最小值),然后遍历数组,如果比它大(小)就更新。
代码
ElementType Max( ElementType S[], int N )
{ElementType maxNum=S[0];for(int i = 1;i<N;i++)if(maxNum<S[i])maxNum=S[i];return maxNum;
}
2. 计算阶乘
思路:
使用递归,把大问题分解为小问题
代码:
int Factorial(int n){if(n==0)return 1;return n*Factorial(n-1);
}
3. 得到数字的每一位
思路
通过不断的模以10,然后再除以10,不断循环,可以把得到每一位存放到数组里面(灵活处理)。
代码
// 一种表达
while(number){array[number%10]++; //使用辅助数组记录每个位出现的次数number/=10;}// 存放每一位在数组中
while(number){array[i++]=number%10; //使用辅助数组记录每位number/=10;}// 判断某一位出现了几次while(number){if(number%10==D)count++;number/=10;}
4. 计算时间类型
思路:可以统一转为分钟之后,统一处理。
time=hour*60+mintue
5. 最大公约数、最小公倍数
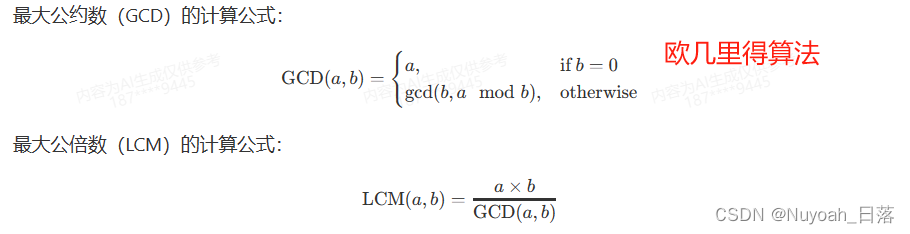
// 最大公约数
int gcd(int a,int b){if(b == 0)return a;return gcd(b,a%b);
}// 最小公倍数
int lcm(int a, int b) {return (a * b) / gcd(a, b);
}
6. 循环数组的思想
题目:猴子选大王
一群猴子要选新猴王。新猴王的选择方法是:让N只候选猴子围成一圈,从某位置起顺序编号为1~N号。从第1号开始报数,每轮从1报到3,凡报到3的猴子即退出圈子,接着又从紧邻的下一只猴子开始同样的报数。如此不断循环,最后剩下的一只猴子就选为猴王。请问是原来第几号猴子当选猴王?
代码
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>int main() {int i, N, arr[1000] = {0}, count=0;scanf("%d", &N);// 存入数组for (i = 0; i < N; i++)arr[i] = i+1;i = 0;while (1) {if (arr[(i + N) % N] != 0) {count++;}if (count % 3 == 0)arr[(i + N) % N] = 0;if (count == 3 * N-2) {printf("%d", arr[(i + N) % N]);break;}i++;}return 0;
}
补充
经典例题
1. 复试四则运算
题目内容
本题要求编写程序,计算2个复数的和、差、积、商。
输入格式:
输入在一行中按照a1 b1 a2 b2的格式给出2个复数C1=a1+b1i和C2=a2+b2i的实部和虚部。题目保证C2不为0。
输出格式:
分别在4行中按照(a1+b1i) 运算符 (a2+b2i) = 结果的格式顺序输出2个复数的和、差、积、商,数字精确到小数点后1位。如果结果的实部或者虚部为0,则不输出。如果结果为0,则输出0.0。
题解
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>int main() {double a1, b1, a2, b2, a[4], b[4];char c[4] = { '+','-','*','/' };scanf("%lf %lf %lf %lf", &a1, &b1, &a2, &b2);a[0] = a1 + a2; b[0] = b1 + b2;a[1] = a1 - a2; b[1] = b1 - b2;a[2] = a1 * a2 - b1 * b2; b[2] = b1 * a2 + b2 * a1;a[3]= (a1 * a2 + b1 * b2) / (pow(a2, 2) + pow(b2, 2));b[3]= (b1 * a2 - a1 * b2) / (pow(a2, 2) + pow(b2, 2));for (int i = 0; i < 4; i++) {if (fabs(a[i]) > 0.05 && fabs(b[i]) > 0.05) {printf("(%.1lf%+.1lfi) %c (%.1lf%+.1lfi) = %.1lf%+.1lfi", a1, b1,c[i], a2, b2, a[i], b[i]);}else if (fabs(b[i]) > 0.05) {printf("(%.1lf%+.1lfi) %c (%.1lf%+.1lfi) = %.1lfi", a1, b1, c[i], a2, b2, b[i]);}else if (fabs(a[i]) > 0.05) {printf("(%.1lf%+.1lfi) %c (%.1lf%+.1lfi) = %.1lf", a1, b1,c[i], a2, b2, a[i]);}else {printf("(%.1lf%+.1lfi) %c (%.1lf%+.1lfi) = %.1lf", a1, b1, c[i],a2, b2, 0);}if(i!=3)printf("\n");}return 0;
}
2. 数列求和
题目内容
给定某数字A(1≤A≤9)以及非负整数N(0≤N≤100000),求数列之和S=A+AA+AAA+⋯+AA⋯A(N个A)。例如A=1, N=3时,S=1+11+111=123。
输入格式:
输入数字A与非负整数N。
输出格式:
输出其N项数列之和S的值。
题解
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include<math.h>int main() {double sum = 0, item = 0;int A, N;scanf("%d %d",&A,&N);for (int i = 0; i < N; i++) {// 和之前的每一项计算不太一样item+= A * pow(10, i);sum += item;}printf("%.lf", sum);return 0;
}相关文章:
算法常用思路总结
思路 1. 求数组中最大最小值思路代码 2. 计算阶乘思路:代码: 3. 得到数字的每一位思路代码 4. 计算时间类型5. 最大公约数、最小公倍数6. 循环数组的思想题目:猴子选大王代码 补充经典例题1. 复试四则运算题目内容题解 2. 数列求和题目内容题…...

Leetcode 3016. Minimum Number of Pushes to Type Word II
Leetcode 3016. Minimum Number of Pushes to Type Word II 1. 解题思路2. 代码实现 题目链接:3016. Minimum Number of Pushes to Type Word II 1. 解题思路 这道题的话思路其实还是蛮简单的,显然我们的目的是要令对给定的word在键盘上敲击的次数最小…...

node.js如何将webp转jpg图片
在Node.js中,可以使用一些库来实现将WebP图像转换为JPEG。一个常用的库是sharp,它是一个快速、高效的图像处理库。以下是一个简单的Node.js脚本示例,演示如何使用sharp库将WebP转换为JPEG: 首先,确保已经安装了sharp库…...

达梦数据库 忘记 SYSDBA 密码 处理方法
DM 提供数据库身份验证模式、基于操作系统的身份验证模式、外部身份验证模式和 UKEY 身份验证模式来保护对数据库访问的安全。数据库身份验证模式需要利用数据库口令, 即在创建或修改用户时指定用户口令,用户在登录时输入对应口令进行身份验证;基于操作 …...

SpringBoot ES 重建 Mapping
SpringBoot ES 重建 Mapping 1 复制数据2 删除老索引3 重建索引4 复制回数据 1 复制数据 POST http://elastic:123456127.0.0.1:9200/_reindex{"source": {"index": "老索引名称"},"dest": {"index": "备份索引名称&q…...

【51单片机】矩阵按键
0、前言 参考:普中 51 单片机开发攻略 1、硬件 2、软件 main.c #include <reg52.h> #include <intrins.h> #include "delayms.h"typedef unsigned int u16; //对数据类型进行声明定义 typedef unsigned char u8; #define GPIO_KEY P1 #d…...

Redis- AOF刷盘策略
在Redis中,appendfsync everysec 是一个与持久化相关的配置选项,它属于 Redis 的 AOF(Append Only File)持久化策略的一部分。 Redis支持两种主要的数据持久化方式:RDB(快照)和AOF(…...

标量、向量、矩阵和张量的区别?
标量、向量、矩阵和张量是数学和物理学中常用的概念,它们在多维数据表示和处理中扮演着关键角色。下面是这些概念的基本区别: 标量(Scalar): -标量是单个数字,用于表示单一的量。 -它没有方向。 -在数学中࿰…...

【51单片机】动态数码管
0、前言 参考: 普中51单片机开发攻略–A2.pdf 1、数码管介绍 上一章我们主要是介绍一位数码管的内部结构及控制原理。下面我们再来介 绍下多位数码管及动态显示原理的相关知识。 1.1 多位数码管简介 2、74HC245 和 74HC138 芯片介绍 2.1 74HC245 芯片简介 2.2 7…...

Webpack5入门到原理22:提升打包构建速度
HotModuleReplacement 为什么 开发时我们修改了其中一个模块代码,Webpack 默认会将所有模块全部重新打包编译,速度很慢。 所以我们需要做到修改某个模块代码,就只有这个模块代码需要重新打包编译,其他模块不变,这样…...

EXCEL VBA获取幸运数字号码
EXCELVBA获取幸运数字号码 以下就是VBA幸运号码产生的程序,复制粘贴到VBA代码框即可运行 Option Base 1 Sub 幸运号码()Dim n As Integer, i As Integer, j As IntegerDim l() As Integern Application.InputBox("请输入需要产生幸运号码的数量:…...

【标准IO】fseek函数、ftell函数、fflush函数、getline函数
目录 fseekftellrewindfflushgetline 橙色 当你在文件中写入了10个字符后,又想把这10个字符读出来,该怎么做呢?因为有文件操作符指针的存在,此时该指针已经指在了这10个字符末尾,所以需要把该指针重定向,这…...

VSCODE使用CMAKE显示命令无法找到
背景:使用了code server,安装CMAKE和CMAKE TOOLS,但是通过ctrlshiftp打开命令面板,运行随便一个cmake指令,都出现了指令无法找到。具体为“命令"CMake: 配置"导致错误 (command ‘cmake.configure’ not fou…...
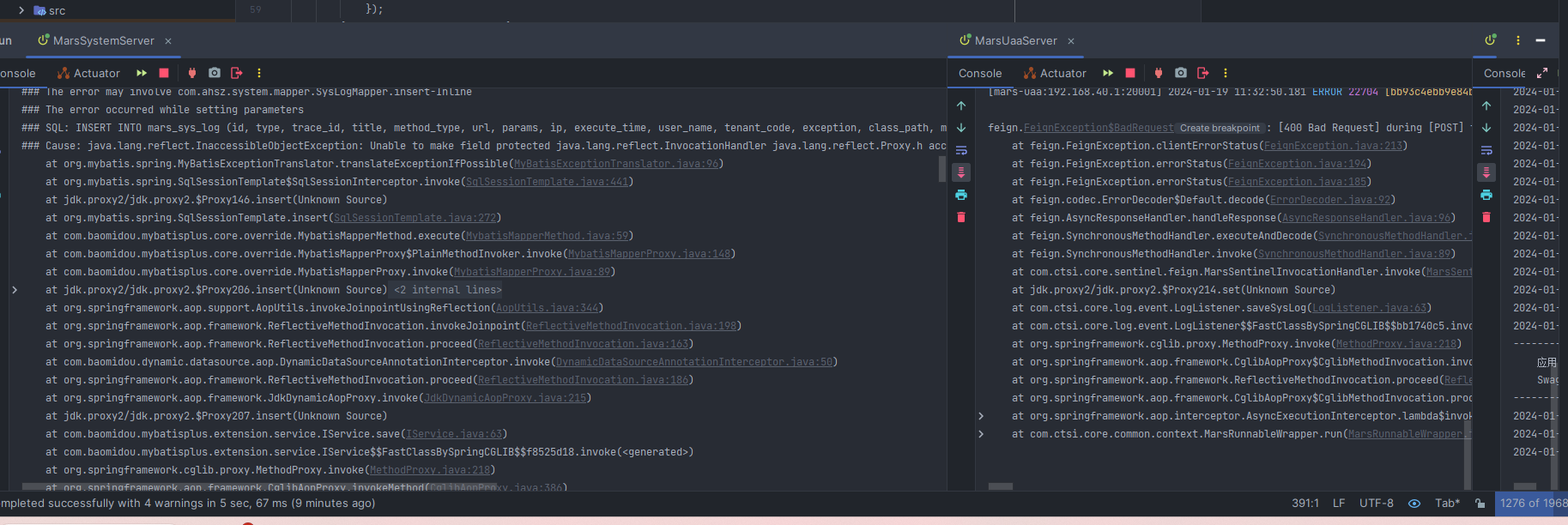
【SpringCloud】微服务框架后端部署详细过程记录20240119
前言:前两天公司接到客户提供的一个微服务框架,导师让我在本地部署验证一下该框架的可用性,借此机会记录一下微服务项目的一个基本部署流程,仅供学习参考,如有不足还请指正! 文件结构 提供的压缩文件共包含…...

《设计模式的艺术》笔记 - 桥接模式
介绍 桥接模式将抽象部分与其实现部分分离,使它们都可以独立地变化。它是一种对象结构型模式,又称为柄体模式或接口模式 实现 myclass.h // // Created by yuwp on 2024/1/12. //#ifndef DESIGNPATTERNS_MYCLASS_H #define DESIGNPATTERNS_MYCLASS_H#…...
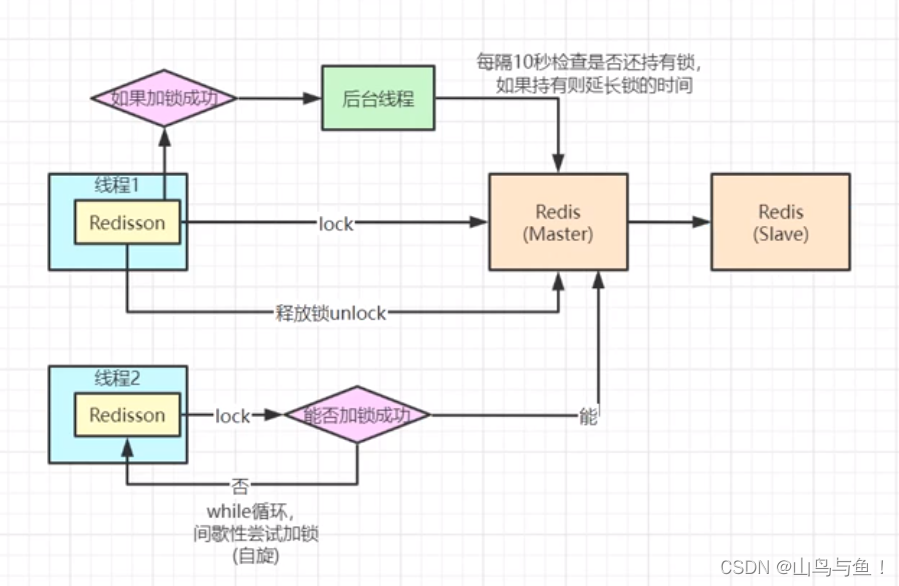
Redis高并发分布式锁
目录 场景描述 订单扣减场景举例 代码调整1 代码调整2 代码调整3 redisson锁续命核心代码 场景描述 订单扣减场景举例 //首先在redis中set stock 300 RequestMapping("/deduct_stock") public String deductStock() {int stock Integer.parseInt(stringRedi…...
)
组件开发遇到的问题(vue的问题)
组件的开发和引用 <template><div class"xx">组件</div> </template> <script>export default {name: viewMore,components: {},data() {return {}}} </script> <style scoped>可以定义组件都有的样式 </style> …...

vue3前端开发,感受一下组合式api和VUE2选项式的差异
vue3前端开发,感受一下组合式api和VUE2选项式的差异!今天开始,正式开始,进入学习Vue3的内容。以后代码,案例分享,都会采用组合式api的模式为大家做展示。 今天是第一节,带大家感受一下,Vue3的组…...

电梯调度问题文献阅读
电梯调度问题文献阅读 文章目录 电梯调度问题文献阅读[toc]文献阅读1. 陈纪龙,孟洪兵,吴刚等.六层电梯模拟系统的研究与实现[J].伊犁师范学院学报(自然科学版),2014,8(01):57-62.2. 陈福兰,杜虹.浅析电梯并联运行的几种调度方法[J].装备制造技术,2012,(10):178-180190.3. 马春江…...

文心一言 VS 讯飞星火 VS chatgpt (183)-- 算法导论13.4 7题
七、用go语言,假设用 RB-INSERT 将一个结点 x 插入一棵红黑树,紧接着又用 RB-DELETE 将它从树中删除。结果的红黑树与初始的红黑树是否一样?证明你的答案。 文心一言: 首先,我们需要明确RB-INSERT和RB-DELETE的基本操…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
