【刷题笔记4】
动态规划题目汇总
斐波那契数列:1,1,2,3,5,8,13……
递归一把解决三类问题:1.数据定义是按照递归的(斐波那契数列)。2.问题解法是按递归算法实现的。 3.数据形式是按照递归形式定义的。
递归的一般形式:
void rec(形参列表)
{if(test) return; //边界条件//!!!注意!!! 递归一定要有边界条件!!!否则就会死循环!!!rec(实参列表) //递归调用语句序列2 //递归返回段(回溯)
}- 有一种兔子,从出生后第3个月起每个月都生一只兔子,小兔子长到第三个月后每个月又生一只兔子。例:假设一只兔子第3个月出生,那么它第5个月开始会每个月生一只兔子。一月的时候有一只兔子,假如兔子都不死,问第n个月的兔子总数为多少?
输入一个int型整数表示第n个月
输出对应的兔子总数
#include <iostream>
using namespace std;
int total(int n);
int total(int n)
{if(n==1||n==2)//这个叫边界条件return 1;elsereturn total(n-1)+total(n-2);//递归调用
}
int main() {//斐波那契数列int n,num;cin>>n;num=total(n);cout<<num;
}- 把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法? 注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5,1)被视为是同一种分法。
解题思路:
假设有m个苹果和n个盘子,我们可以将问题分为两种情况: 1. 盘子中至少有一个盘子为空:这种情况下,我们可以将m个苹果放在n-1个盘子中,即将问题转化为将m个苹果放在n-1个盘子中的分法。所以,这种情况下的分法数为f(m, n-1)。 2. 盘子中所有盘子都有苹果:这种情况下,我们可以将每个盘子中放入一个苹果,然后将剩余的m-n个苹果放在n个盘子中,即将问题转化为将m-n个苹果放在n个盘子中的分法。所以,这种情况下的分法数为f(m-n, n)。 综上所述,将m个苹果放在n个盘子中的分法数为f(m, n) = f(m, n-1) + f(m-n, n)。
边界条件: - 当m=0时,表示没有苹果需要放入盘子中,所以只有一种分法,即所有盘子都为空。 - 当n=0时,表示没有盘子可以放苹果,所以没有分法。 根据上述递推关系和边界条件,可以使用递归或动态规划的方法来求解。
#include <iostream>
using namespace std;int fn(int m,int n)
{if(n<1) return 0;if(m<0) return 0;if(m==0) return 1;return fn(m-n,n)+fn(m,n-1);//没有空盘子+有1个空盘子
}int main() {int m,n;cin>>m>>n;cout<<fn(m,n);
}- n*m的棋盘格子(n为横向的格子数,m为竖向的格子数)从棋盘左上角出发沿着边缘线从左上角走到右下角,总共有多少种走法,要求不能走回头路,即:只能往右和往下走,不能往左和往上走。
#include <iostream>
using namespace std;
int digui(int x,int y)
{if(x==1||y==1)//只有一行或者一列的时候,就有x+y种方法return x+y; //否则就往上或者往下走一步。return digui(x-1,y)+digui(x,y-1);//if(x==0)//return 1;//if(y==0)//return 1;//return x+y; //否则就往上或者往下走一步。//return digui(x-1,y)+digui(x,y-1);//if(m<0||n<0)//return 0;//else if(n==1&&m==0)//return 1;//else if(m==1&&n==0)//return 1;//else //return(digui(m-1, n)+digui(m,n-1));
}int main() {int m,n;cin>>n>>m;cout<<digui(m,n);}最长递增子序列问题:

4.
class Solution {public:int LIS(vector<int>& arr) {if (arr.empty())return 0;int N = arr.size();vector<int>dp(N, 1);int maxLen = 1;for (int i = 1; i < N; i++) {for (int j = 0; j < i; j++) {if (arr[i] > arr[j]) {dp[i] = max(dp[i], dp[j] + 1); //长度加1}}maxLen = max(maxLen, dp[i]);//更新最大长度}return maxLen;}};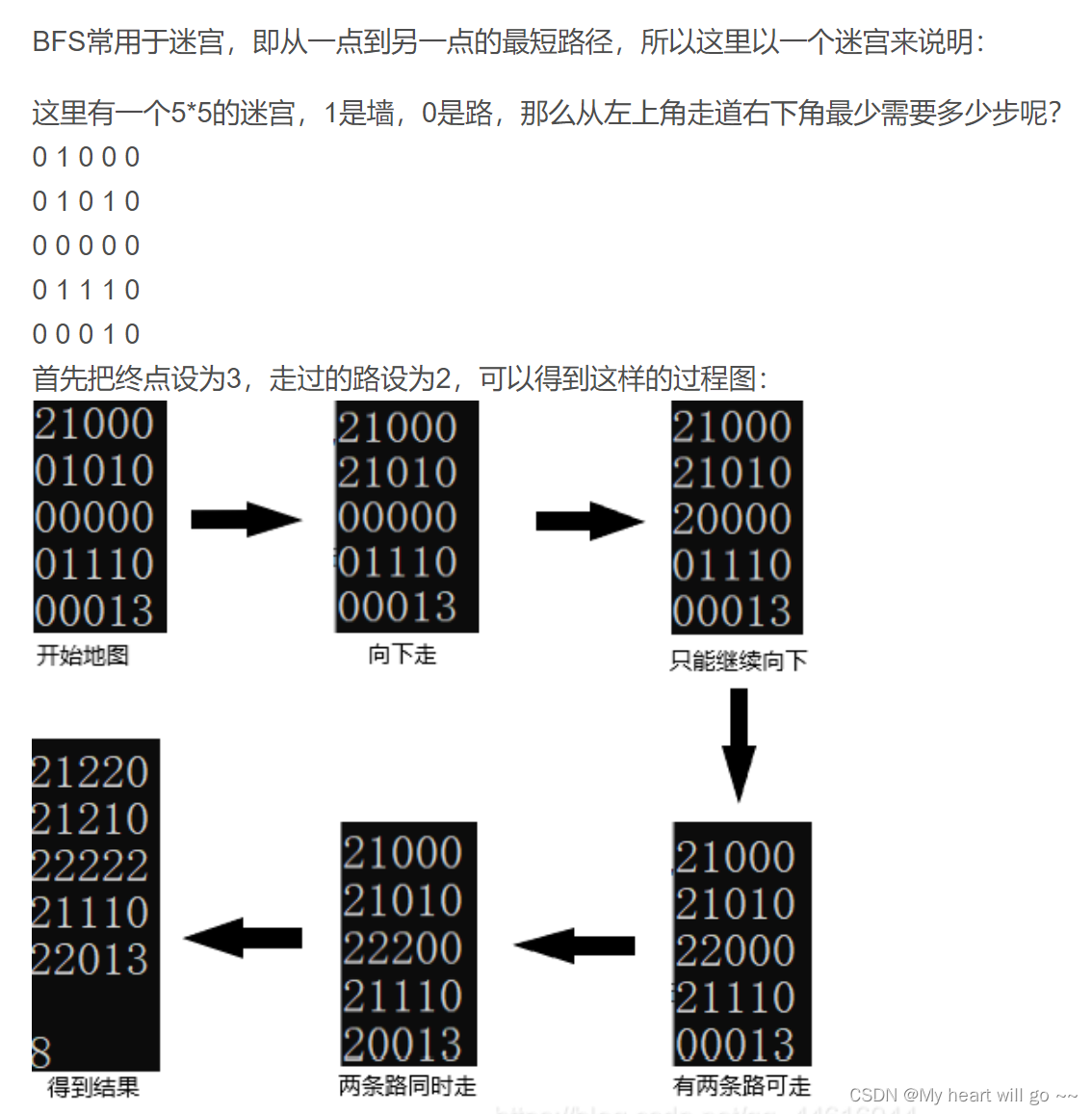
- BFS(广度优先搜索算法)
#include <iostream>
#include <cstdio>
#include <queue>
using namespace std;
int Map[5][5]; //定义地图大小
int dir[4][2]= {1,0,-1,0,0,-1,0,1}; //定义方向
int n,m,ans;
struct node
{int x,y,step;} now,nextt; //保存走步
int BFS(int x,int y)
{queue<node>q;int xx,yy,zz;Map[x][y]=2; //走过初始点now.x=x;now.y=y;now.step=0;q.push(now); //从当前点开始while(!q.empty()){now=q.front();q.pop();for(int i=0; i<4; i++) //遍历四个方向{xx=now.x+dir[i][0];yy=now.y+dir[i][1]; //走一步if(xx>=0&&xx<5&&yy>=0&&yy<5&&Map[xx][yy]!=1&&Map[xx][yy]!=2) //可以走{nextt.x=xx;nextt.y=yy;nextt.step=now.step+1; //步数加一Map[now.x][now.y]=2; //走过一个点if(Map[xx][yy]==3) //到达终点return nextt.step;q.push(nextt);}for(int i=0; i<5; i++){ //打印地图for(int j=0; j<5; j++)cout << Map[i][j];cout << endl;}cout << endl;}}return -1; //走不过去
}int main()
{for(int i=0; i<5; i++) //输入地图for(int j=0; j<5; j++)cin >> Map[i][j];Map[4][4]=3; //定义终点ans=BFS(0,0);cout << ans<< endl;return 0;}自己重构的走迷宫的代码:
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <queue>
#include <vector>
using namespace std;
int n,m;
int zuiyou;
vector<vector<int>>maze; //定义地图大小
struct point{int x,y;
};
int fangxiang[4][2]={{-1,0},{1,0},{0,-1},{0,1}}; //定义上下左右
vector<vector<int> >path(5,vector<int>(5));//记录每次的方向,0,1,2,3对应上下左右
vector<vector<int>>fan;struct node{int x,y,z;
}now, nextt;;void bfs(int x,int y)
{ // vector<vector<int>> path(n, vector<int>(m));maze[x][y]=2;queue <node> q;now.x=x;now.y=y;now.z=0;q.push(now);while(!q.empty()){ now=q.front();maze[now.x][now.y]=2;q.pop();for( int i=0;i<4;i++){int xx=now.x+fangxiang[i][0];int yy=now.y+fangxiang[i][1];if(xx>=0&&xx<n&&yy>=0&&yy<m&&maze[xx][yy]==3){ path[xx][yy]=i;if(maze[xx][yy]==3)zuiyou=now.z+1;}if(xx>=0&&xx<n&&yy>=0&&yy<m&&maze[xx][yy]==0){ nextt.x=xx;nextt.y=yy;nextt.z=now.z+1;q.push(nextt);path[xx][yy]=i;}}}int ii=n-1,jj=m-1;fan.push_back({ii,jj});while(ii!=0||jj!=0){ int num=path[ii][jj];ii=ii-fangxiang[num][0]; jj=jj-fangxiang[num][1]; fan.push_back({ii,jj});}reverse(fan.begin(),fan.end());
}int main()
{ cin>>n>>m;maze=vector<vector<int>>(n,vector<int>(m)); //定义地图大小 for(int i=0;i<n;i++){for(int j=0;j<m;j++){cin>>maze[i][j];}}maze[4][4]=3;bfs(0, 0);cout<<zuiyou<<endl;;cout<<endl;for(auto t:fan){cout<<t[0]<<","<<t[1];cout<<endl;}}
- DFS(深度优先搜索算法):一般用于查找图中的路径、连通性检测、拓扑排序等。
深度优先搜索使用栈(Stack)数据结构来保存需要探索的节点。每次访问一个节点时,将其标记为已访问,并将其未访问的邻居节点压入栈中。然后从栈中弹出一个节点,继续访问该节点的未访问邻居节点,直到栈为空。
如果需要找到最短路径,可以考虑使用其他算法,如广度优先搜索(BFS)或 Dijkstra 算法。一般最小步数、最短距离、最小操作次数等问题采用BFS。
相关文章:

【刷题笔记4】
动态规划题目汇总 斐波那契数列:1,1,2,3,5,8,13…… 递归一把解决三类问题:1.数据定义是按照递归的(斐波那契数列)。2.问题解法是按递归算法实现的。 3.数据…...
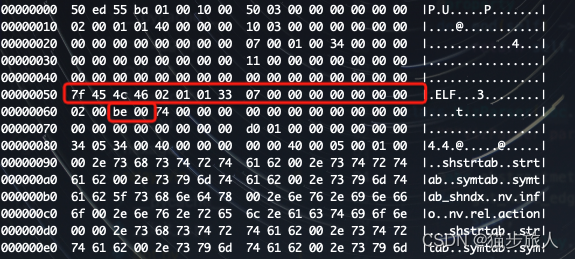
cuda二进制文件中到底有些什么
大家好。今天我们来讨论一下,相比gcc编译器编译的二进制elf文件,包含有 cuda kernel 的源文件编译出来的 elf 文件有什么不同呢? 之前研究过一点 tvm。从 BYOC 的框架中可以得知,前端将模型 partition 成 host 和 accel(accel 表…...

怎么从视频中提取动图?一个方法快速提取gif
视频以连续的方式播放一系列图像帧,通过每秒播放的帧数(帧率)来创做,由于GIF动图则以循环播放一系列静态图像帧的方式展现动画效果。由于视频的优势在于流畅的动画、丰富的细节和长时间播放,因此常用于电影、电视节目、…...

String字符串的比较和hash函数减少哈希冲突
1.为什么比较字符串通过hash值比通过字符串本身效率更高 比较两个字符串的哈希值相对于比较两个字符串本身的效率更高,原因如下: 哈希函数具有快速计算的特性:哈希函数可以将一个字符串转换为一个固定长度的哈希值。这个转换过程通常是非常…...

【数据库原理】(38)数据仓库
数据仓库(Data Warehouse, DW)是为了满足企业决策分析需求而设计的数据环境,它与传统数据库有明显的不同。 一.数据库仓库概述 定义: 数据仓库是一个面向主题的、集成的、相对稳定的、反映历史变化的数据集合,用于支持企业管理和…...
已有标准库的拓展和修改)
C++17新特性(四)已有标准库的拓展和修改
这一部分介绍C17对已有标准库组件的拓展和修改。 1. 类型特征拓展 1.1 类型特征后缀_v 自从C17起,对所有返回值的类型特征使用后缀_v,例如: std::is_const_v<T>; // C17 std::is_const<T>::value; // C11这适用于所有返回值的…...
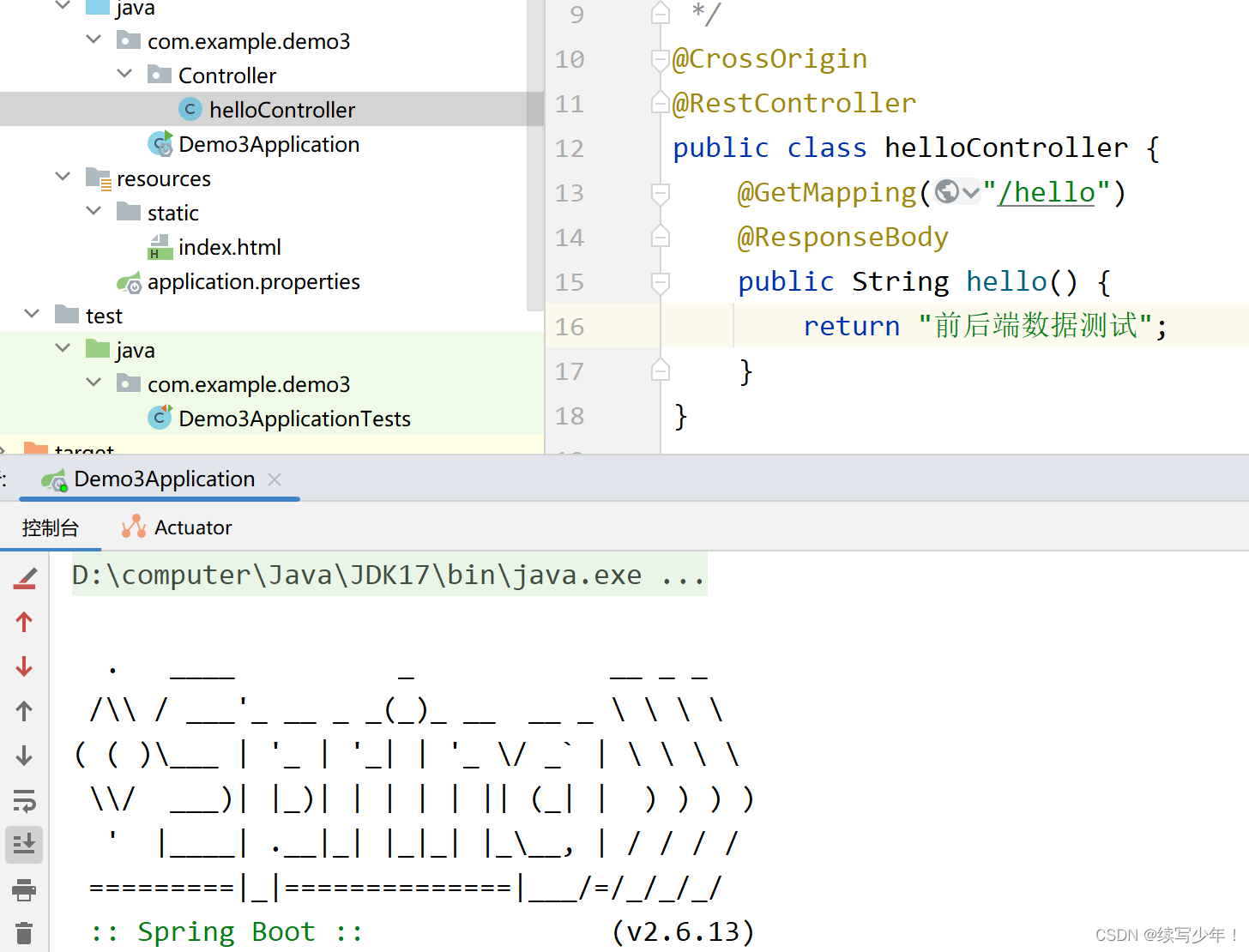
软件是什么?前端,后端,数据库
软件是什么? 由于很多东西没有实际接触,很难理解,对于软件的定义也是各种各样。但是我还是不理解,软件开发中的前端,后端,数据库到底有什么关系呢! 这个问题足足困扰了三年半,练习时…...
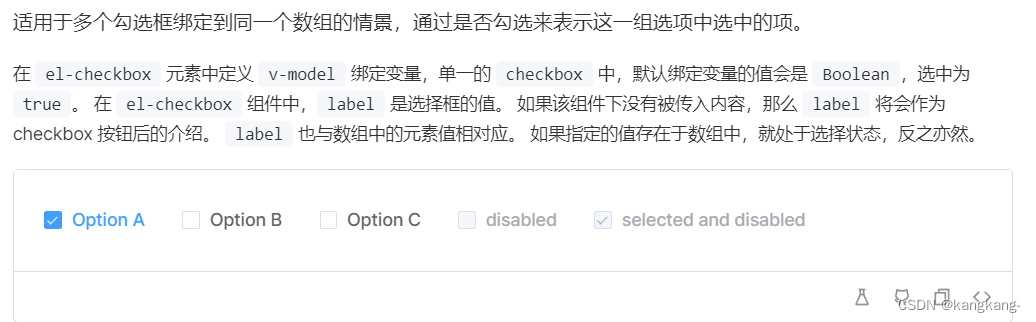
Vue3+ElementUI 多选框中复选框和名字点击方法效果分离
现在的需求为 比如我点击了Option A ,触发点击Option A的方法,并且复选框不会取消勾选,分离的方法。 <el-checkbox-group v-model"mapWork.model_checkArray.value"> <div class"naipTypeDom" v-for"item …...

设计模式篇章(4)——十一种行为型模式
这个设计模式主要思考的是如何分配对象的职责和将对象之间相互协作完成单个对象无法完成的任务,这个与结构型模式有点像,结构型可以理解为静态的组合,例如将不同的组件拼起来成为一个更大的组件;而行为型更是一种动态或者具有某个…...
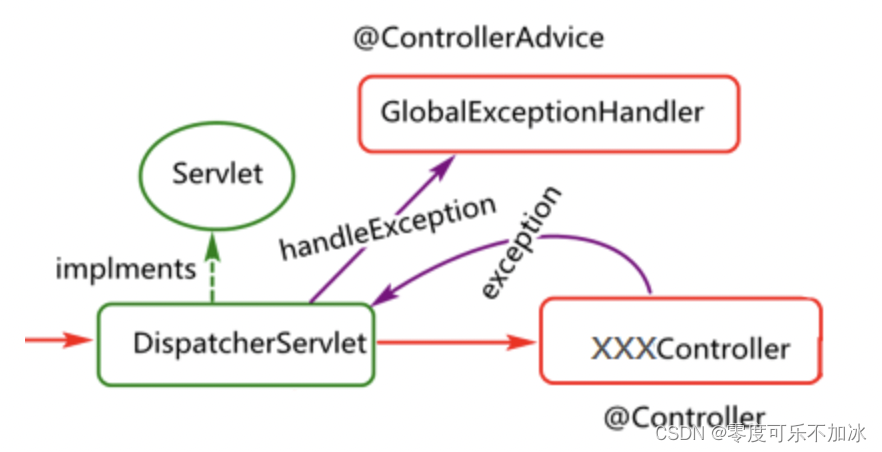
Spring成长之路—Spring MVC
在分享SpringMVC之前,我们先对MVC有个基本的了解。MVC(Model-View-Controller)指的是一种软件思想,它将软件分为三层:模型层、视图层、控制层 模型层即Model:负责处理具体的业务和封装实体类,我们所知的service层、poj…...
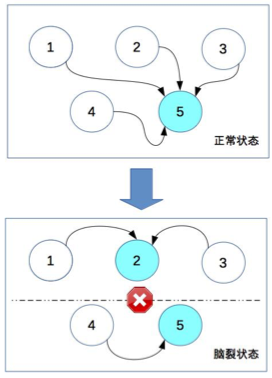
架构篇05-复杂度来源:高可用
文章目录 计算高可用存储高可用高可用状态决策小结 今天,我们聊聊复杂度的第二个来源高可用。 参考维基百科,先来看看高可用的定义。 系统无中断地执行其功能的能力,代表系统的可用性程度,是进行系统设计时的准则之一。 这个定义…...

C#调用Newtonsoft.Json将bool序列化为int
使用Newtonsoft.Json将数据对象序列化为Json字符串时,如果有布尔类型的属性值时,一般会将bool类型序列化为字符串,true值序列化为true,false值序列化为false。如下面的类型序列化后的结果如下: public class UserInfo…...

【Linux系统编程】环境变量详解
文章目录 1. 环境变量的基本概念2. 如何理解呢?(测试PATH)2.1 切入点1查看具体的环境变量原因剖析常见环境变量 2.2 切入点2给PATH环境变量添加新路径将我们自己的命令拷贝到PATH已有路径里面 2.3 切入点3 3. 显示所有环境变量4. 测试HOME5. …...

智能合约介绍
莫道儒冠误此生,从来诗书不负人 目录 一、什么是区块链智能合约? 二、智能合约的发展背景 三、智能合约的优势 四、智能合约的劣势 五、一些关于智能合约的应用 总结 一、什么是区块链智能合约? 智能合约,是一段写在区块链上的代码,一…...
Python自动化实战之接口请求的实现
在前文说过,如果想要更好的做接口测试,我们要利用自己的代码基础与代码优势,所以该章节不会再介绍商业化的、通用的接口测试工具,重点介绍如何通过 python 编码来实现我们的接口测试以及通过 Pycharm 的实际应用编写一个简单接口测…...

react和vue的区别
一、核心思想不同 Vue的核心思想是尽可能的降低前端开发的门槛,是一个灵活易用的渐进式双向绑定的MVVM框架。 React的核心思想是声明式渲染和组件化、单向数据流,React既不属于MVC也不属于MVVM架构。 如何理解React的单向数据流? React的单…...

Spring 中有哪些方式可以把 Bean 注入到 IOC 容器?
目录 1、xml方式2、CompontScan Component3、使用 Bean方式4、使用Import 注解5、FactoryBean 工厂 bean6、使用 ImportBeanDefinitionRegistrar 向容器中注入Bean7、实现 ImportSelector 接口 1、xml方式 使用 xml 的方式来声明 Bean 的定义,Spring 容器在启动的…...

客户需求,就是项目管理中最难管的事情
对于需求控制和管理 个人的观点是:首先要向客户传递开发流程,第二必须制作原型,需求确认时确认的是原型,而不是需求文档,第三,开发阶段要快速迭代,与客户互动。管人方面我想对于项目经理来讲&am…...

条款28:避免返回 handles 指向对象的内部成分
创建一个矩形的类(Rectangle),为保持Rectangle对象较小,可以只在其对象中保存一个指针,用于指向辅助的结构体,定义其范围的点数据存放在辅助的结构体中: class Point { // 表示点的类 public:P…...
)
【人工智能】之深入理解 AI Agent:超越代码的智能助手(2)
人工智能(AI)正在以前所未有的速度迅猛发展,而AI Agent(智能代理)则是这一领域中备受瞩目的一环。AI Agent 不仅仅是程序的执行者,更是能够感知、学习和交互的智能实体。本文将深入探讨什么是 AI Agent&…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

五、jmeter脚本参数化
目录 1、脚本参数化 1.1 用户定义的变量 1.1.1 添加及引用方式 1.1.2 测试得出用户定义变量的特点 1.2 用户参数 1.2.1 概念 1.2.2 位置不同效果不同 1.2.3、用户参数的勾选框 - 每次迭代更新一次 总结用户定义的变量、用户参数 1.3 csv数据文件参数化 1、脚本参数化 …...
