leetcode_贪心算法
贪心算法相关题
- 简单题目
- 455.分发饼干
- 1005.K次取反后最大化的数组和
- 860.柠檬水找零
- 序列问题
- 376.摆动序列
- 法一:贪心法
- 法二:动态规划
- 单调递增的数字
- 简化版本
- 有点难度
- 53.最大子序和
- 贪心算法
- 动态规划
- 134.加油站
- 968.监控二叉树
- 两个维度权衡问题
- 分发糖果
- 406.根据身高重建队列
- 贪心解决股票问题
- 122.买卖股票的最佳时机II
- 贪心法
- 动规法
- 区间问题
- 55.跳跃游戏
- 贪心法
- 45.跳跃游戏II
- 动态规划
- 452.用最少数量的箭引爆气球
- 435.无重叠区间
- 736.划分字母区间
- 56.合并区间
- 补充(改版自弓箭数量那题)
- 贪心
简单题目
455.分发饼干
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(),g.end());sort(s.begin(),s.end());int count=0,i=0,j=0;while(i<g.size()&&j<s.size()){if(s[j]>=g[i]) {count++;i++;}j++;}return count;}
};
1005.K次取反后最大化的数组和
class Solution {
public:static bool cmp(int a,int b){return abs(a)>abs(b);}int largestSumAfterKNegations(vector<int>& nums, int k) {sort(nums.begin(),nums.end(),cmp);int sum=0;for(int i =0;i<nums.size();i++){if(nums[i]<0&&k>0){nums[i] = -nums[i];k--;}}if(k%2==1) nums[nums.size()-1]*=-1;for(int i =0;i<nums.size();i++){sum+=nums[i];}return sum;}
};
860.柠檬水找零
class Solution {
public:bool lemonadeChange(vector<int>& bills) {map<int,int> map1;for(int i =0;i<bills.size();i++){if(bills[i]==5)map1[5]++;if(bills[i]==10){map1[5]--;map1[10]++;if(map1[5]<0) return false;}if(bills[i]==20){if(map1[10]){map1[5]--;map1[10]--;}else{map1[5]-=3;}map1[20]++;if(map1[5]<0||map1[10]<0) return false;}} return true; }
};
序列问题
376.摆动序列
法一:贪心法
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。
我们根据正常理解,可以总结出我们需要统计波动的数量,定义prediff(nums[i]-nums[i-1])和curdiff(nums[i+1]-nums[i]),则波动需要满足的条件是:(prediff<0&&curdiff>0) || (prediff>0&&curdiff<0)。
但是这样会忽略平坡的情况,平坡分两种,
-
一是上下坡中有平坡,对于这种情况,我们只统计一个波动就好,默认统计prediff=0的情况,就是平坡在前,上下坡在后,统计这一波动,这对应的也是代码随想录中提到的删除平坡中左面的元素。
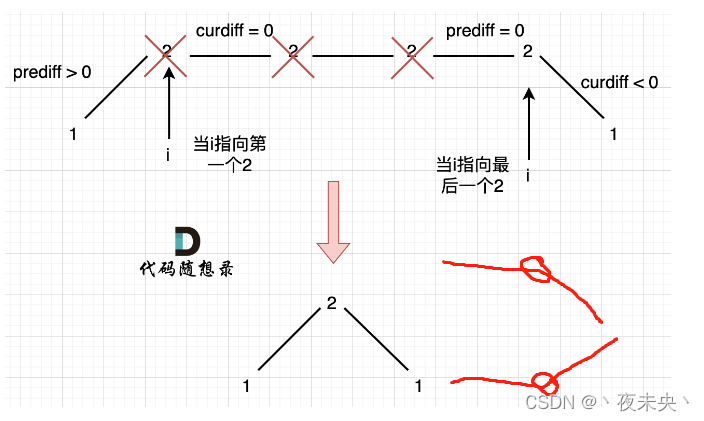
-
二是单调坡中有平坡,这对应的是我们应该修改对于prediff的更新,因为单调坡中的拐点使用上面的条件确实会被统计两次。
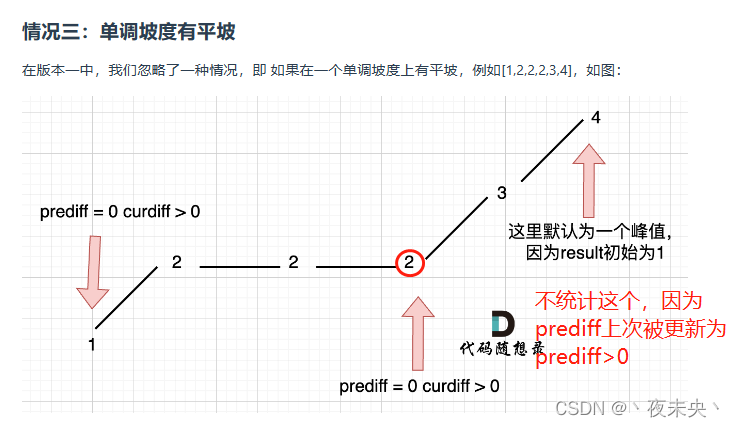
最后考虑两个数以及数组两端的情况,默认最右面有一个峰值(res=1起步),两个数的话无法判断写死摆动序列为2.
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if(nums.size()==2) {if(nums[0]!=nums[1]) return nums.size();if(nums[0]==nums[1]) return 1;}int prediff=0,curdiff=0,res=1;for(int i =0;i<nums.size()-1;i++){curdiff=nums[i+1]-nums[i];if(prediff<=0&&curdiff>0||prediff>=0&&curdiff<0){res++;prediff=curdiff;}}return res;}
};
法二:动态规划
dp数组含义:
- dp[i][0]:表示考虑前i个数,第i个数作为山峰的摆动子序列最长长度
- dp[i][1]:表示考虑前i个数,第i个数作为山谷的摆动子序列最长长度
递推表达式:
dp[i][0] = max(dp[i][0],dp[j][1]+1) 其中0<j<i,其nums[j]<nums[i],表示将nums[i]接到某个山谷后面作为山峰的最长长度。
dp[i][1] = max(dp[i][1],dp[j][0]+1) 其中0<j<i,其nums[j]>nums[i],表示将nums[i]接到某个山峰后面作为山谷的最长长度
class Solution {
public:int dp[1010][2];int wiggleMaxLength(vector<int>& nums) {memset(dp,0,sizeof(dp));dp[0][0]=dp[0][1] = 1;for(int i =1;i<nums.size();i++){dp[i][0] = dp[i][1] = 1;for(int j =0;j<i;j++)if(nums[i]>nums[j]) dp[i][0] = max(dp[i][0],dp[j][1]+1);for(int j=0;j<i;j++)if(nums[i]<nums[j]) dp[i][1] = max(dp[i][1],dp[j][0]+1);}return max(dp[nums.size()-1][0],dp[nums.size()-1][1]);}
};
单调递增的数字
class Solution {
public:int monotoneIncreasingDigits(int n) {if (n < 10) return n;string str = "";while (n) {char c = n % 10 + '0';str += c;n = n / 10;}reverse(str.begin(), str.end());for(int i =1;i<str.size();i++){if(str[i]<str[i-1]){str[i-1]-=1;for(int j=i;j<str.size();j++){str[j]='9';}for(int k=i-2;k>=0;k--){if(str[k]>str[k+1]){str[k]-=1;str[k+1]='9';}}}}int num = 0;for (int i = 0; i < str.size(); i++) {num = num*10+str[i] - '0';}return num;}
};
简化版本
从后往前遍历,如果出现strNum[i - 1] > strNum[i]的情况,则strNum[i - 1]–,然后一直用一个flag记录i的位置,以便于之后将i之后所有卫生纸上的数字
class Solution {
public:int monotoneIncreasingDigits(int N) {string strNum = to_string(N);// flag用来标记赋值9从哪里开始// 设置为这个默认值,为了防止第二个for循环在flag没有被赋值的情况下执行int flag = strNum.size();for (int i = strNum.size() - 1; i > 0; i--) {if (strNum[i - 1] > strNum[i] ) {flag = i;strNum[i - 1]--;}}for (int i = flag; i < strNum.size(); i++) {strNum[i] = '9';}return stoi(strNum);}
};
有点难度
53.最大子序和
贪心算法
class Solution {
public:int maxSubArray(vector<int>& nums) {int count=0,res=INT32_MIN;for(int i =0;i<nums.size();i++){count+=nums[i];res = count>res?count:res;if(count<=0) count=0;}return res;}
};
动态规划
这道题写动规的时候,dp的含义直接设置成了前i个连续子数组的最大和,没有再设置res去保存最大值,导致dp[i]在更新的时候到底是最大值还是只是和的时候,出现了两层表示意义。比如1,2,3,-7,6,dp[3] = 6,但dp[3]按照原有含义,没有办法直接+nums[4]。
class Solution {
public:int dp[100010];int maxSubArray(vector<int>& nums) {memset(dp,0,sizeof(dp));int res = nums[0];dp[0] = nums[0];for(int i =1;i<nums.size();i++){dp[i] = max(dp[i-1]+nums[i],nums[i]);if(dp[i]>res) res=dp[i];}return res;}
};
134.加油站
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int min_gas = 0,sum_gas=0;for(int i =0;i<gas.size();i++){sum_gas=sum_gas+gas[i]-cost[i];if(sum_gas<min_gas) min_gas=sum_gas;}if(sum_gas<0) return -1;else{sum_gas=0;for(int i=gas.size()-1;i>=0;i--){sum_gas+=gas[i]-cost[i];if(sum_gas>=-min_gas){return i;}}}return -1;}
};
968.监控二叉树
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:// 0:表示该节点没有被覆盖// 1:表示该节点有摄像头// 2:表示该节点被覆盖int ans;int traversal(TreeNode* cur){if(cur==nullptr) return 2;int left = traversal(cur->left);int right = traversal(cur->right);if(left==0||right==0) {ans++;return 1;}if(left==1||right==1){return 2;}if(left==2||right==2){return 0;}return -1;}int minCameraCover(TreeNode* root) {int root_num = traversal(root);if(root_num==0) ans++;return ans;}
};
两个维度权衡问题
分发糖果
class Solution {
public:int candy(vector<int>& ratings) {vector<int> candy(ratings.size(),1);for(int i=1;i<ratings.size();i++){if(ratings[i]>ratings[i-1]){candy[i] = candy[i-1]+1;}}for(int i=ratings.size()-1;i>0;i--){if(ratings[i-1]>ratings[i]){candy[i-1]=max(candy[i]+1,candy[i-1]);}}int ans=0;for(int i =0;i<candy.size();i++){ans+=candy[i];}return ans; }
};
406.根据身高重建队列
现根据身高从大到小排列,再根据k一个一个插入。
class Solution {
public:static bool cmp(vector<int>& a,vector<int>& b){if(a[0]==b[0]) return a[1]<b[1];else return a[0]>b[0];}vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {sort(people.begin(),people.end(),cmp);vector<vector<int>> que;for(int i =0;i<people.size();i++){int position = people[i][1];que.insert(que.begin()+position,people[i]);}return que;}
};
贪心解决股票问题
122.买卖股票的最佳时机II
贪心法
class Solution {
public:int maxProfit(vector<int>& prices) {int sum=0;for(int i =1;i<prices.size();i++){if(prices[i]-prices[i-1]>0){sum+=prices[i]-prices[i-1];}}return sum;}
};
动规法
class Solution {
public:int dp[30010];int maxProfit(vector<int>& prices) {memset(dp,0,sizeof(dp));int sum=0;for(int i =1;i<prices.size();i++){dp[i]=dp[i-1] + max(prices[i]-prices[i-1],0);}return dp[prices.size()-1];}
};
区间问题
区间问题总结,除了两个跳跃游戏。我们一共左了四个区间的贪心算法题。用最少弓箭射爆气球,五重叠区间的个数,划分字母区间和合并区间。用最少的弓箭射爆气球,实际上我们要找的是重叠区间的个数,而射爆气球这道题认为[1,2],[2,3]不属于重叠区间,这需要注意。我们按照左边界排序后,只需要遍历interval中每一个右边界,每次更新重叠区间的右端点r=min(points[i][1],r)r = \text {min}(\text{points}[i][1],r)r=min(points[i][1],r),然后处理每个interval左边界和r的关系就好。无重叠区间的个数实际上总区间个数减去重叠区间个数,所以看清楚条件[1,2],[2,3]属不属于重叠情况确立等号是否成立。划分字母区间这道题有点难度,需要统计每个字符出现的最远位置下标然后处理。合并区间,按左边界排序后,然后从左到右遍历看是否是重叠的,然后更新合并区间的左边界右边界。
55.跳跃游戏
贪心法
class Solution {
public:bool canJump(vector<int>& nums) {int step=0;if(nums.size()==1) return true;for(int i =0;i<=step;i++){step=max(i+nums[i],step);if(step>=nums.size()-1) return true;}return false;}
};
45.跳跃游戏II
动态规划
class Solution {
public://我的思路是:dp数组表示到第i个格子需要的最短次数//dp数组更新的递推公式是:从j=0个格子开始找int dp[10100];int jump(vector<int>& nums) {memset(dp, 10010, sizeof(dp));if (nums.size() == 1) return 0;else dp[0] = 0;for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (j + nums[j] >= i) {dp[i] = min(dp[j] + 1, dp[i]);break;}}}return dp[nums.size() - 1];}
};
452.用最少数量的箭引爆气球
class Solution {
public:static bool cmp(vector<int>& a, vector<int>& b){if(a[0]==b[0]) return a[1]<b[1];else return a[0]<b[0];}int findMinArrowShots(vector<vector<int>>& points) {sort(points.begin(),points.end(),cmp);int l=points[0][0],r=points[0][1];int ans=1;for(int i =1;i<points.size();i++){l = points[i][0];r = min(points[i][1],r);if(l>r){r=points[i][1];ans++;}}return ans;}
};
435.无重叠区间
class Solution {
public://无重叠区间的个数等于总区间个数减去重叠区间个数static bool cmp(vector<int>& a,vector<int>& b){if(a[1]==b[1]) return a[0]<b[0];else return a[1]<b[1];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {//这里需要记一下,按右边界排序要从左向右找//按左边界排序,要从右向左找sort(intervals.begin(),intervals.end(),cmp);int l=intervals[0][0],r=intervals[0][1];int ans=1;for(int i =1;i<intervals.size();i++){if(intervals[i][0]>=r){ans++;r=intervals[i][1];}}return intervals.size()-ans;}
};
736.划分字母区间
这道题不用回溯,不是所有的划分字母区间都要回溯,这道题主要在于统计之前遍历过所有字母的最远边界,如果当前下标到达了这个最远边界,说明到达了字符串的分割点。
class Solution {
public://贪心法map<char,int> mp;vector<int> ans;vector<int> partitionLabels(string s) {for(int i =0;i<s.size();i++){mp[s[i]] = i;}int split=0,split1=-1;for(int i =0;i<s.size();i++){if(mp[s[i]]>split) split=mp[s[i]];if(i==split){ans.push_back(split-split1);split1= split;} }return ans;}
};
56.合并区间
通过做这道题,我先是按照解上面题的常规套路,按照右边界排序,后来发现很多bug,这道合并区间的题如果从左到右遍历一定是先按左边界排列。
class Solution {
public:static bool cmp(vector<int>&a, vector<int>&b){if(a[0]==b[0]) return a[1]<b[1];else return a[0]<b[0];}vector<vector<int>> res;vector<vector<int>> merge(vector<vector<int>>& intervals) {sort(intervals.begin(),intervals.end(),cmp);int l = intervals[0][0];int r = intervals[0][1];for(int i =1;i<intervals.size();i++){if(intervals[i][0]<=r){r = max(intervals[i][1],r);}else{res.push_back({l,r});l = intervals[i][0];r = intervals[i][1];}}res.push_back({l,r});return res;}
};
补充(改版自弓箭数量那题)
class Solution {
public://无重叠区间的个数等于总区间个数减去重叠区间个数static bool cmp(vector<int>& a, vector<int>& b){if(a[0]==b[0]) return a[1]<b[1];else return a[0]<b[0];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {sort(intervals.begin(),intervals.end(),cmp);int l=intervals[0][0],r=intervals[0][1];int ans=1;for(int i =1;i<intervals.size();i++){l = intervals[i][0];r = min(intervals[i][1],r);if(l>=r){ //加个等号,认为等于的情况不属于交叉区间r=intervals[i][1];ans++;}}return intervals.size()-ans;}
};
贪心
要从覆盖范围出发,不管怎么跳,覆盖范围一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了重点得到的就是最小步数。
class Solution {
public:int jump(vector<int>& nums) {if(nums.size()==1) return 0;int curmaxindex = 0; // 当前覆盖最远距离下标,当前位置为i的话,能走到的最远距离就是i+nums[i]。int nextmaxindex = 0; // 记录走的最大步数int step = 0; // 下一步覆盖最远距离下标for(int i =0;i<=curmaxindex;i++){nextmaxindex = max(nums[i]+i,nextmaxindex); // 更新下一步能走到的最远距离if(i==curmaxindex){ // 如果i已经走到了当前能走到的最大距离if(curmaxindex<nums.size()-1){step++; // 那么我们一定要走下一步了,但下一步的落脚点在哪儿不用管// 不要误认为下一步落脚点一定是curdistance,这个没关系curmaxindex=nextmaxindex; // 更新当前覆盖最远距离下标if(nextmaxindex>=nums.size()-1) break; // 下一步的覆盖范围已经可以达到终点,结束循环}}}return step;}
};
相关文章:

leetcode_贪心算法
贪心算法相关题简单题目455.分发饼干1005.K次取反后最大化的数组和860.柠檬水找零序列问题376.摆动序列法一:贪心法法二:动态规划单调递增的数字简化版本有点难度53.最大子序和贪心算法动态规划134.加油站968.监控二叉树两个维度权衡问题分发糖果406.根据…...
C语言每日一题】——杨氏矩阵
【C语言每日一题】——倒置字符串😎前言🙌杨氏矩阵🙌总结撒花💞😎博客昵称:博客小梦 😊最喜欢的座右铭:全神贯注的上吧!!! 😊作者简介…...
最佳iOS设备管理器imazing 2.16.9官网Mac/Windows下载电脑版怎么下载安装
imazing 2.16.9官网Mac/Windows下载电脑版是款针对苹果设备所打造的管理工具。iMazing为用户提供多种设备管理功能,每一位用户都能以自己的形式管理苹果设备。iMazing与苹果设备连接后,用户就可以轻松传输文件,浏览保存信息等。 应用介绍 iM…...

八大排序算法之堆排序的实现+经典TopK问题
目录 一.堆元素的上下调整接口 1.前言 2.堆元素向上调整算法接口 3.堆元素向下调整算法接口 二.堆排序的实现 1.空间复杂度为O(N)的堆排序(以排升序为例) 思路分析: 代码实现: 排序测试: 时空复杂度分析: 2. 空间复杂度为O(1)的堆排序(以排降序为例) 将数组arr调…...
使用AppSmith(PagePlug )低代码平台快速构建小程序应用实践
文章目录一、入门(一)介绍(二)功能特性(三)体验一下(四)参考教程二、使用Appsmith构建商城微信小程序(一)说明(二)应用配置࿰…...

第52章 短信验证服务和登录的后端定义实现
1 Services.Messages.SmsValidate using Core.Domain.Messages; using Data; using Microsoft.EntityFrameworkCore; namespace Services.Messages { /// <summary> /// 【短信验证服务--类】 /// <remarks> /// 摘要: /// 通过类中的方法成员实…...
谷歌验证码的使用
1. 表单重复提交之验证码 1.1 表单重复提交三种常见情况 提交完表单。服务器使用请求转来进行页面跳转。这个时候,用户按下功能键 F5,就会发起最后一次的请求。造成表单重复提交问题。解决方法:使用重定向来进行跳转用户正常提交服务器&…...
- git的安装与配置)
Git学习入门(1)- git的安装与配置
title: git学习(1) - git的安装与配置CSDN: https://blog.csdn.net/jj6666djdbbd?typeblogBlog: https://helloylh.comGithub: https://github.com/luumodtags: gitabbrlink: 12001description: 本文主要讲解了git的安装,配置基本工作date: …...

【Python】使用Playwright断言方法验证网页和Web应用程序状态
作为测试框架,Playwright 提供了一系列断言方法,您可以使用它们来验证网页和 Web 应用程序的状态。在这篇博客中,田辛老师将介绍 Playwright 中可用的各种断言方法,并为每种方法提供示例。 assert page.url() expected_url &…...

libgdx导入blender模型
具体就是参考 官网 https://libgdx.com/wiki/graphics/3d/importing-blender-models-in-libgdx blender 教程可以看八个案例教程带你从0到1入门blender【已完结】 这里贴一下过程图。 1.初始环境搭建略过。 2.打开blender 选中摄像机和灯光,右键进行删除。 3.选中…...
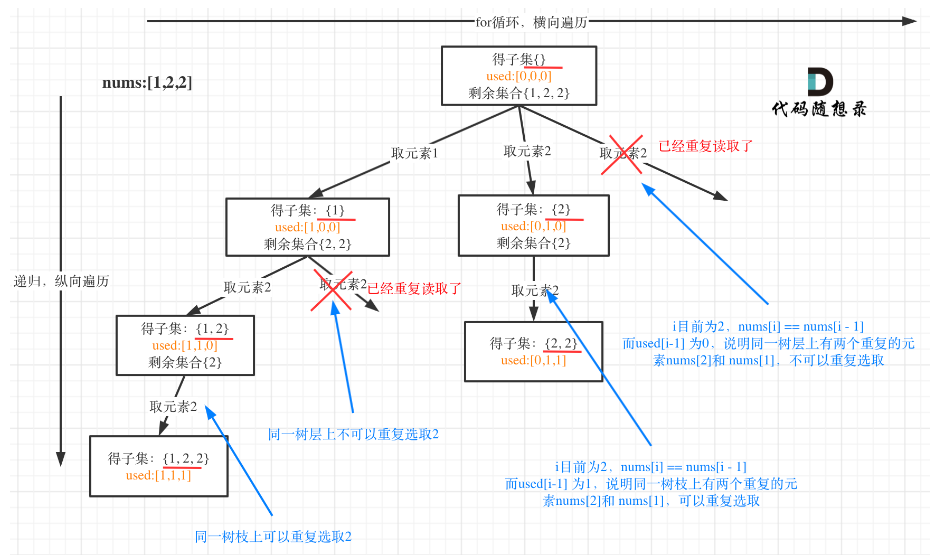
【20230227】回溯算法小结
回溯法又叫回溯搜索法,是搜索的一种方式。回溯法本质是穷举所有可能。如果想让回溯法高效一些,可以加一些剪枝操作。回溯算法解决的经典问题:组合问题切割问题子集问题排列问题棋盘问题如何去理解回溯法?回溯法解决的问题都可以抽…...
centos安装rocketmq
centos安装rocketmq1 下载rocketmq二进制包2 解压二进制包3 修改broker.conf4 修改runbroker.sh和runserver.sh的JVM参数5 启动NameServer和Broker6 安装rockermq dashboard(可视化控制台)1 下载rocketmq二进制包 点击rocketmq二进制包下载地址,下载完成之后通过ft…...
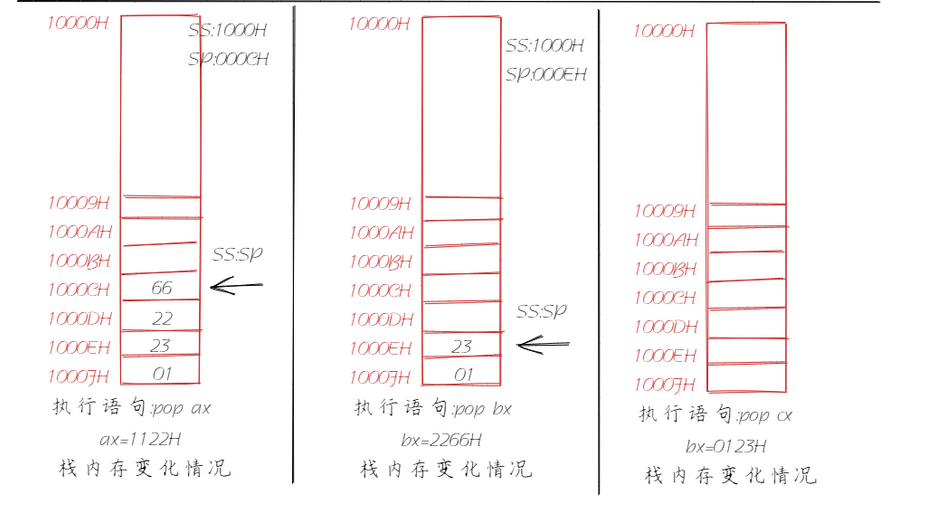
汇编语言程序设计(二)之寄存器
系列文章 汇编语言程序设计(一) 寄存器 在学习汇编的过程中,我们经常需要操作寄存器,那么寄存器又是什么呢?它是用来干什么的? 它有什么分类?又该如何操作?… 你可能会有许多的…...

华为OD机试Golang解题 - 单词接龙 | 独家
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...

Elasticsearch的搜索命令
Elasticsearch的搜索命令 文章目录Elasticsearch的搜索命令数据准备URI Searchq(查询字符串)analyzer(指定查询字符串时使用的分析器)df(指定查询字段)_source(指定返回文档的字段)s…...

为什么人们宁可用Lombok,也不把成员设为public?
目录专栏导读一、从零了解JavaBean1、基本概念2、JavaBean的特征3、JavaBean的优点二、定义最简单的JavaBean三、思考一个问题,为何属性是private,然后用get/set方法?四、下面系统的分析以下,why?五、不和谐的声音,禁…...
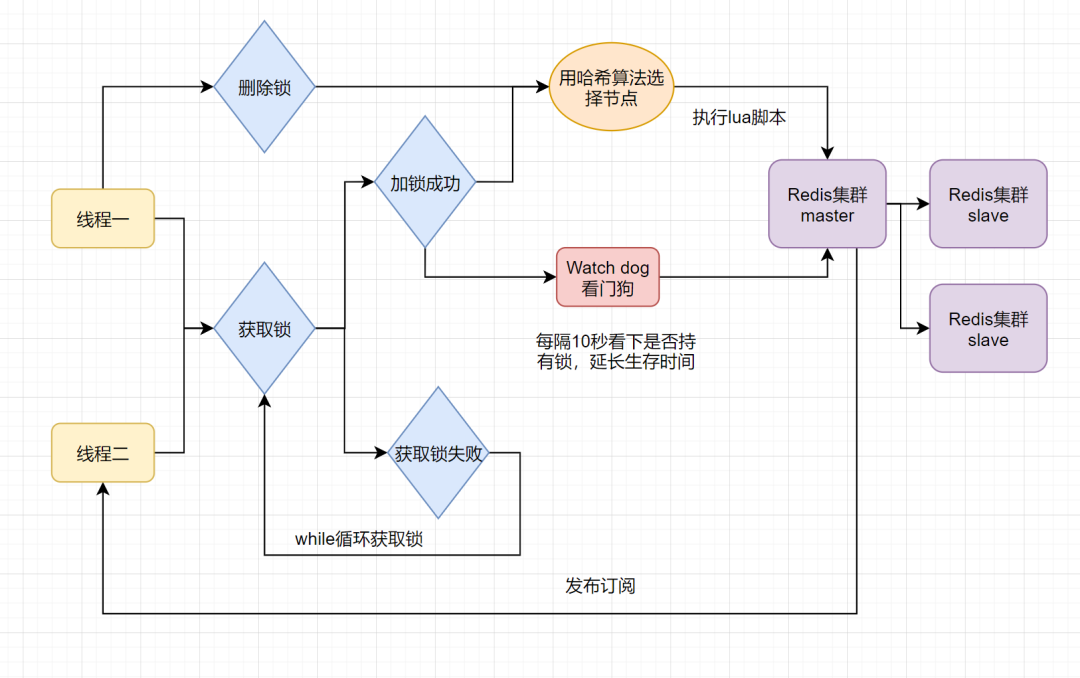
【Redis】Redis 如何实现分布式锁
Redis 如何实现分布式锁1. 什么是分布式锁1.1 分布式锁的特点1.2 分布式锁的场景1.3 分布式锁的实现方式2. Redis 实现分布式锁2.1 setnx expire2.2 set ex px nx2.3 set ex px nx 校验唯一随机值,再删除2.4 Redisson 实现分布式锁1. 什么是分布式锁 分布式锁其实…...
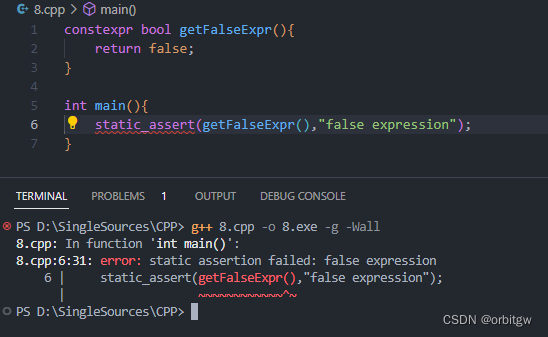
C++ 断言
文章目录前言assertstatic_assert前言 断言(Assertion)是一种常用的编程手段,用于排除程序中不应该出现的逻辑错误。它是一种很好的Debug工具。其作用是判断表达式是否为真。C提供了assert和static_assert来进行断言。在C库中也有断言,其中断言与C的相同…...
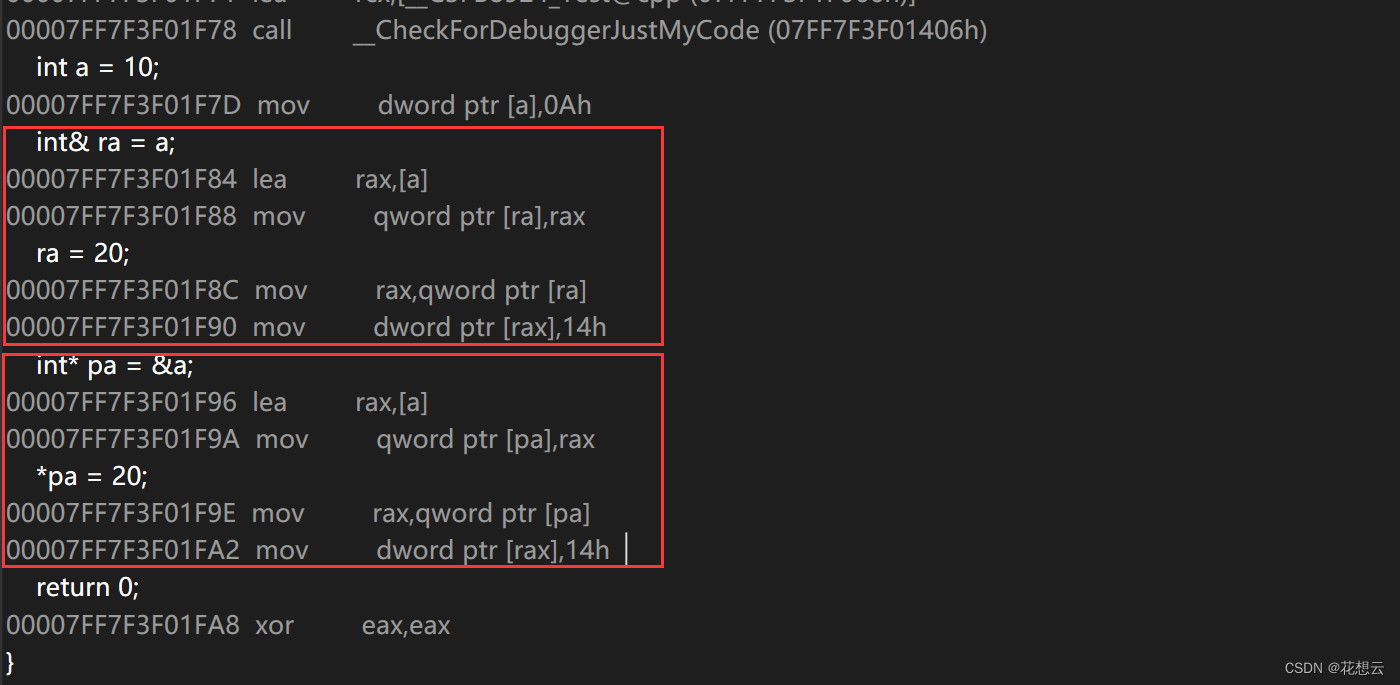
C++修炼之练气期第五层——引用
目录 1.引用的概念 2.引用的性质 3.常量引用 4.使用场景 1.作参数 2.作返回值 5.传值与传引用的效率比较 6.值和引用作为返回值的性能比较 7.引用与指针 指针与引用的不同点 要说C语言中哪个知识点最难学难懂,大部分人可能和我一样的答案——指针。C既然…...
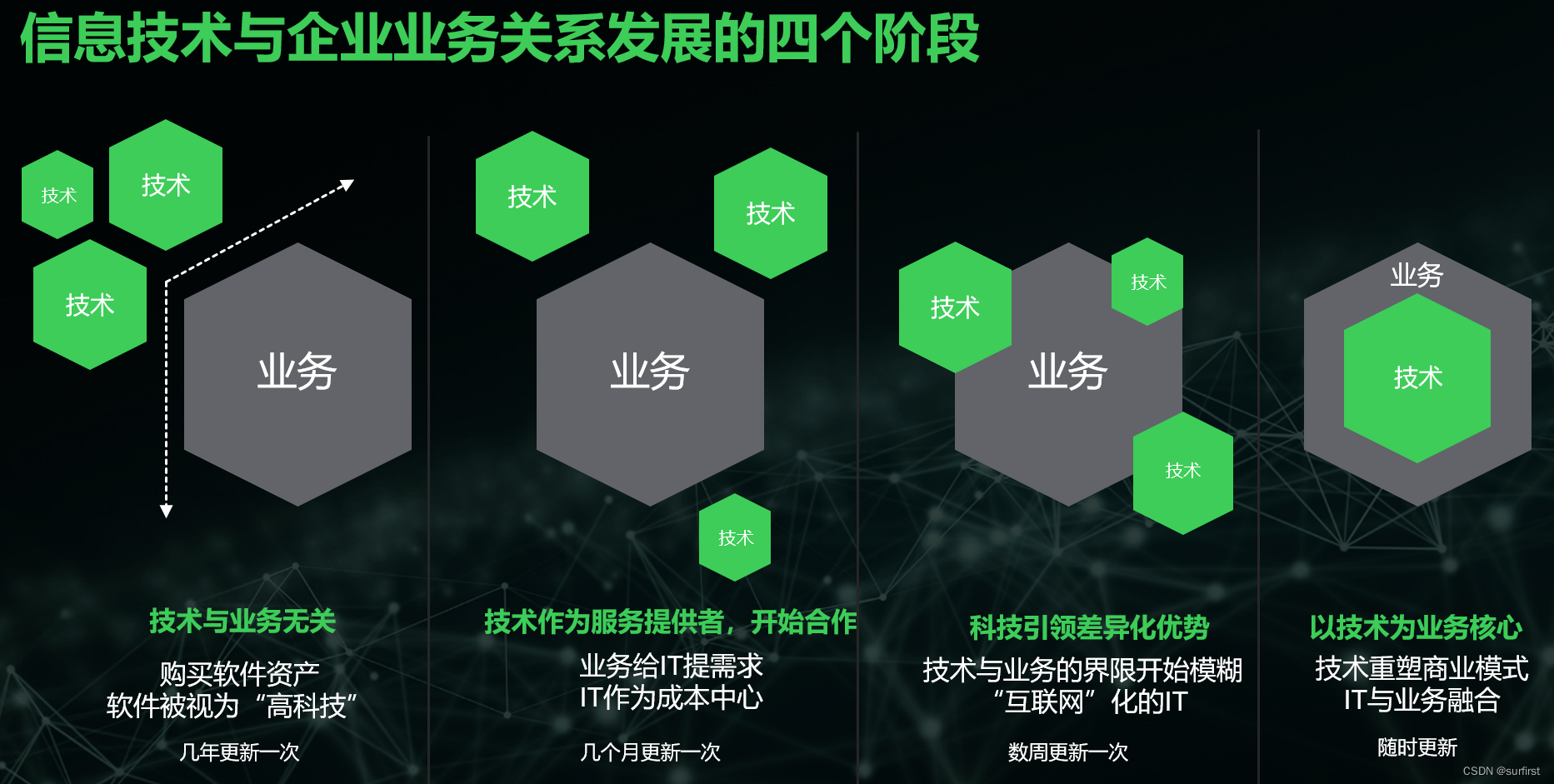
从企业数字化发展的四个阶段,看数字化创新战略
《Edge: Value-Driven Digital Transformation》一书根据信息技术与企业业务发展的关系把企业的数字化分为了四个阶段: 技术与业务无关技术作为服务提供者开始合作科技引领差异化优势以技术为业务核心 下图展示了这四个阶段的特点: 通过了解和分析各个…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
