算法训练营Day45
#Java #动态规划
Feeling and experiences:
最长公共子序列:力扣题目链接
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
注意这里是找的 子序列 ,不需要连续!
dp数组 的创建 和 定义 :
dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
class Solution {public int longestCommonSubsequence(String text1, String text2) {//两个字符串 的 公共子序列(最长)//动态规划 解法//创建dp数组,定义: dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]int [][]dp = new int[text1.length()+1][text2.length()+1];//循环,递推:for (int i = 1 ; i <= text1.length() ; i++) {char char1 = text1.charAt(i - 1);for (int j = 1; j <= text2.length(); j++) {char char2 = text2.charAt(j - 1);if (char1 == char2) { dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[text1.length()][text2.length()];}
}
递推过程:我们使用两个嵌套循环来填充 dp 数组。外循环控制字符串 text1 的长度(从1到text1.length()),而内循环控制字符串 text2 的长度(从1到text2.length())。
字符匹配检查: 在内循环中,我们检查 text1[i-1] 和 text2[j-1] 是否相等。如果相等,说明找到了一个公共字符,我们将 dp[i][j] 设置为 dp[i-1][j-1] + 1。
字符不匹配处理: 如果字符不相等,我们需要考虑哪个方向的公共子序列更长,即取 dp[i-1][j] 和 dp[i][j-1] 中的最大值。
能建立出dp数组,这道题的代码是很简单的。
不相交的线:力扣题目链接
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
-
nums1[i] == nums2[j] - 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:
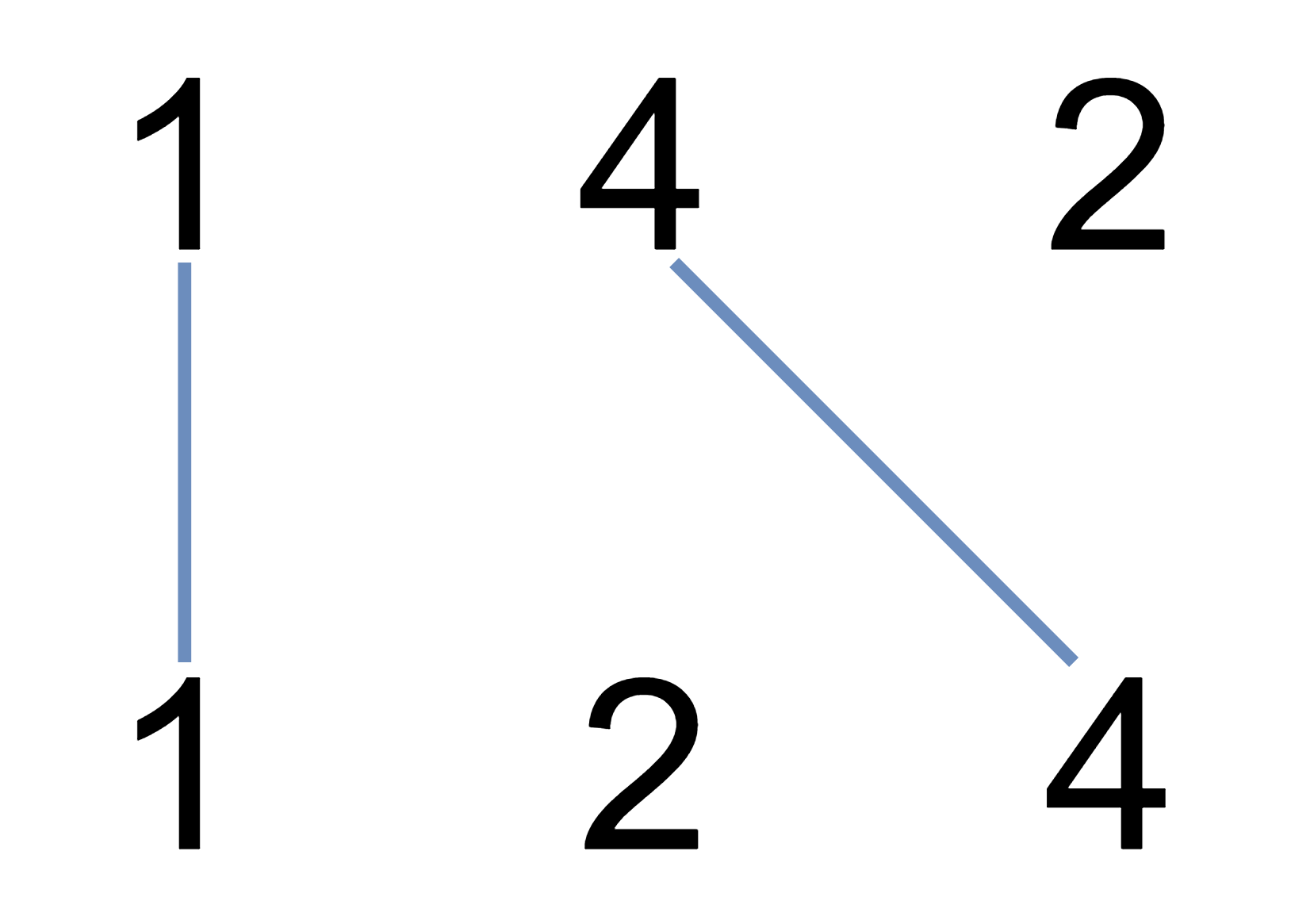
输入:nums1 = [1,4,2], nums2 = [1,2,4] 输出:2 解释:可以画出两条不交叉的线,如上图所示。 但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
该题有个难点 就是不能交叉。
(其实,经过画图推导可知,这道题其实是和上一期是一模一样的)
class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {//类似于找最长子序列长度//创建dp数组int[][]dp = new int[nums1.length+1][nums2.length+1];//循环,递推for(int i =1;i<=nums1.length;i++){for(int j =1;j<=nums2.length;j++){//相同元素if(nums1[i-1] == nums2[j-1]){dp[i][j] = dp[i-1][j-1] +1;}else{dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);}}}return dp[nums1.length][nums2.length];}
}加了一些条件,看着很迷糊,比如什么不能交叉
其实就是找最长公共子序列!
最大子序和:力扣题目链接
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
这道题首先想到的是贪心,之前也用贪心思想解过:
class Solution {public int maxSubArray(int[] nums) {//初始化为数组的第一个元素int maxSum = nums[0];int sum = 0;for(int i = 0;i<nums.length;i++){sum += nums[i];sum = Math.max(sum,nums[i]);maxSum = Math.max(maxSum,sum);}return maxSum;}
}其思路就是:把数组从头开始遍历叠加,如果加上了当前这个数nums[i], 结果比nums[i]还小,说明之前的sum 和 为负数,因为只有这样才会出现这种状况(当前元素,比前面元素的和加上当前元素还大) ,用max函数得到最后的结果!
用动态规划:dp数组
class Solution {public int maxSubArray(int[] nums) {//除了贪心的思想,用动态规划建立dp数组来解答//创建dp数组,含义 到第 i 个元素,得到的最大和为 dp[i]int [] dp = new int[nums.length];int res = nums[0];//初始化dp[0] = nums[0];//循环 ,递推for(int i = 1;i<nums.length;i++){dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);res = Math.max(res,dp[i]);}return res;}
}思路都是一样的,只是写法不一样,这里用到了dp数组
红藕香残玉簟秋,轻解罗裳,独上兰舟。
Fighting!
相关文章:

算法训练营Day45
#Java #动态规划 Feeling and experiences: 最长公共子序列:力扣题目链接 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新…...
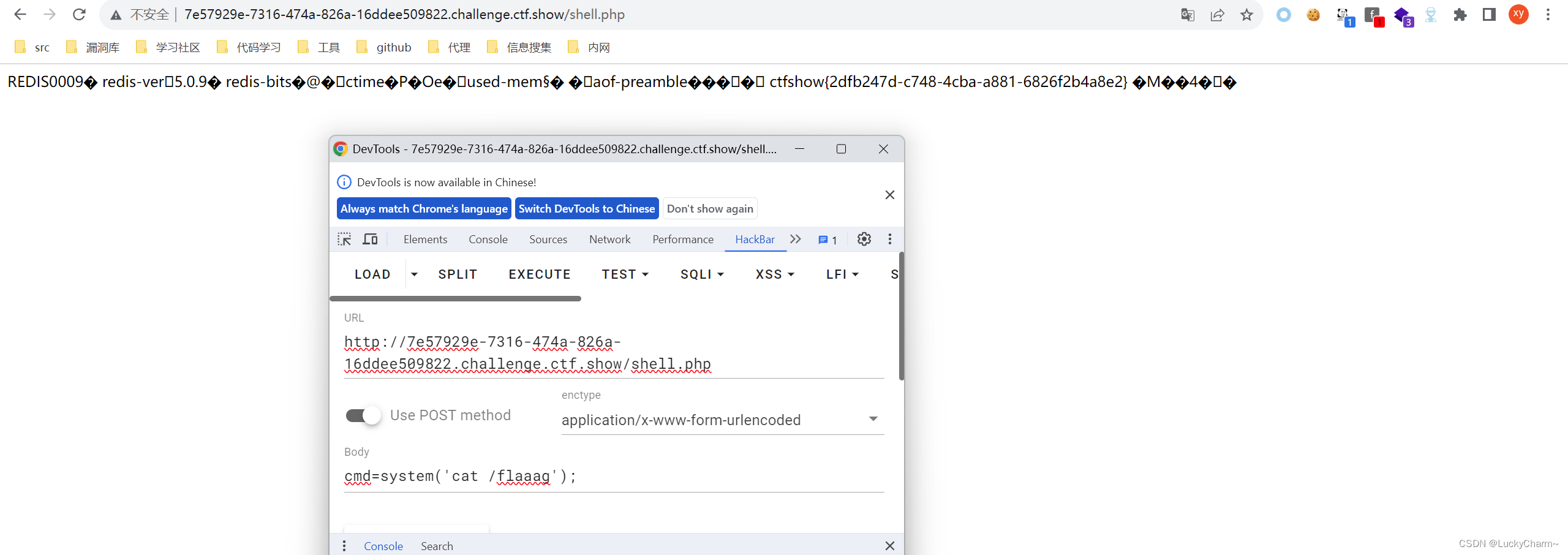
【Redis漏洞利用总结】
前言 redis是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库,并提供多种语言的API。Redis默认使用 6379 端口。 一、redis未授权访问漏洞 0x01 漏洞描述 描述: Redis是一套开源的使用ANSI C编写、支持网络、可基于内存…...
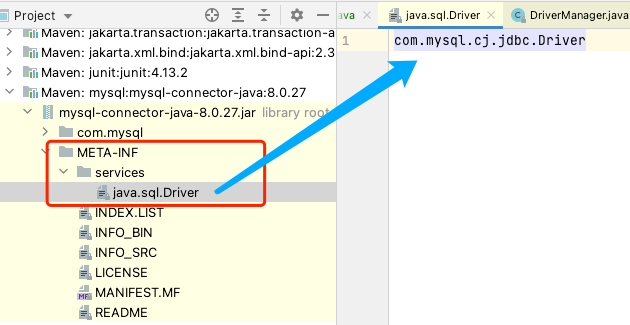
SPI 动态服务发现机制
SPI(Service Provier Interface)是一种服务发现机制,通过ClassPath下的META—INF/services文件查找文件,自动加载文件中定义的类,再调用forName加载; spi可以很灵活的让接口和实现分离, 让API提…...
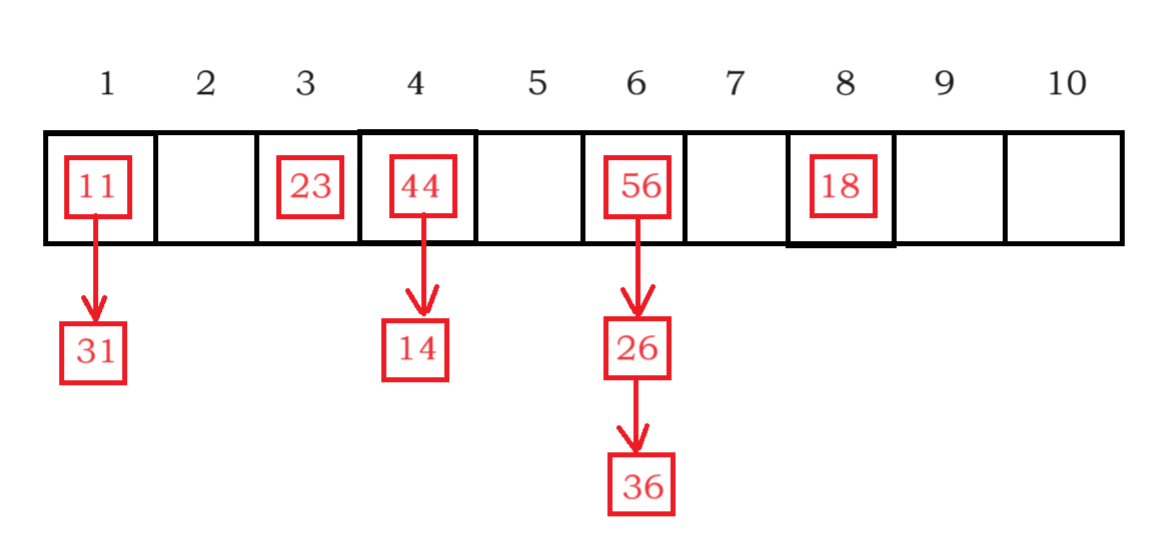
【C++进阶07】哈希表and哈希桶
一、哈希概念 顺序结构以及平衡树中 元素关键码与存储位置没有对应关系 因此查找一个元素 必须经过关键码的多次比较 顺序查找时间复杂度为O(N) 平衡树中为树的高度,即O( l o g 2 N log_2 N log2N) 搜索效率 搜索过程中元素的比较次数 理想的搜索方法:…...

Go 语言实现冒泡排序算法的简单示例
以下是使用 Go 语言实现冒泡排序算法的简单示例: package mainimport "fmt"func bubbleSort(arr []int) {n : len(arr)for i : 0; i < n-1; i {for j : 0; j < n-i-1; j {if arr[j] > arr[j1] {// 交换元素arr[j], arr[j1] arr[j1], arr[j]}}}…...
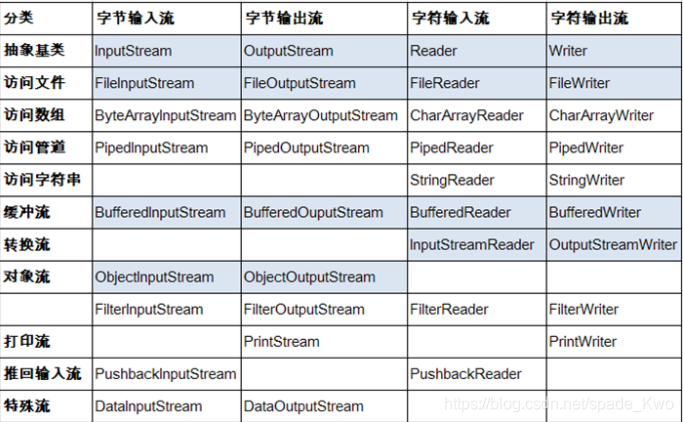
JAVA 学习 面试(五)IO篇
BIO是阻塞I/O,NIO是非阻塞I/O,AIO是异步I/O。BIO每个连接对应一个线程,NIO多个连接共享少量线程,AIO允许应用程序异步地处理多个操作。NIO,通过Selector,只需要一个线程便可以管理多个客户端连接࿰…...
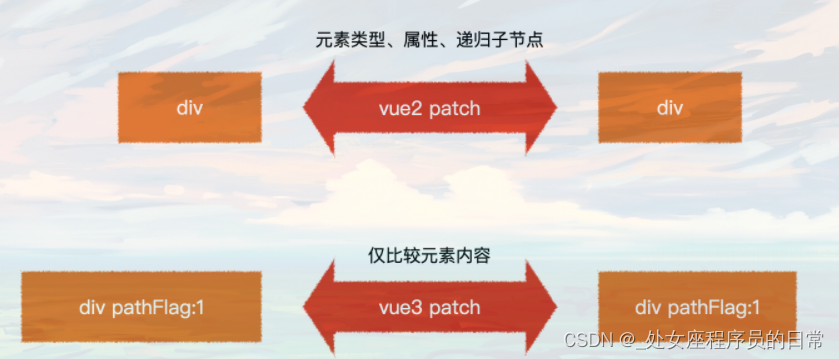
vue3相比vue2的效率提升
1、静态提升 2、预字符串化 3、缓存事件处理函数 4、Block Tree 5、PatchFlag 一、静态提升 在vue3中的app.vue文件如下: 在服务器中,template中的内容会变异成render渲染函数。 最终编译后的文件: 1.静态节点优化 那么这里为什么是两部分…...

web terminal - 如何在mac os上运行gotty
gotty可以让你使用web terminal的方式与环境进行交互,实现终端效果 假设你已经配置好了go环境,首先使用go get github.com/yudai/gotty命令获取可执行文件,默认会安装在$GOPATH/bin这个目录下,注意如果你的go版本比较高ÿ…...
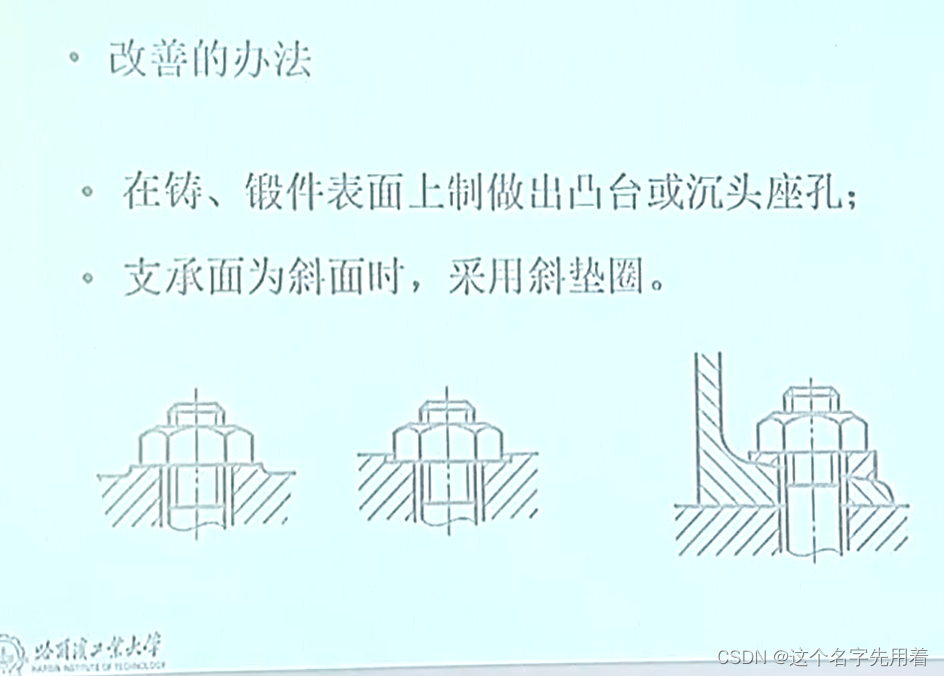
机械设计-哈工大课程学习-螺纹连接
圆柱螺纹主要几何参数螺纹参数 ①外径(大径),与外螺纹牙顶或内螺纹牙底相重合的假想圆柱体直径。螺纹的公称直径即大径。 ②内径(小径),与外螺纹牙底或内螺纹牙顶相重合的假想圆柱体直径。 ③中径ÿ…...

ai绘画|stable diffusion的发展史!简短易懂!!!
手把手教你入门绘图超强的AI绘画,用户只需要输入一段图片的文字描述,即可生成精美的绘画。给大家带来了全新保姆级教程资料包 (文末可获取) 一、stable diffusion的发展史 本文目标:学习交流 对于熟悉SD的同学&#x…...

水塘抽样算法
水塘抽样算法 1、问题描述 最近经常能看到面经中出现在大数据流中的随机抽样问题 即:当内存无法加载全部数据时,如何从包含未知大小的数据流中随机选取k个数据,并且要保证每个数据被抽取到的概率相等。 假设数据流含有N个数,我…...
easyui渲染隐藏域<input type=“hidden“ />为textbox可作为分割条使用
最近在修改前端代码的时候,偶然发现使用javascript代码渲染的方式将<input type"hidden" />渲染为textbox时,会显示一个神奇的效果,这个textbox输入框并不会隐藏,而是显示未一个细条,博主发现非常适合…...

100天精通Python(实用脚本篇)——第113天:基于Tesseract-OCR实现OCR图片文字识别实战
文章目录 专栏导读1. OCR技术介绍2. 模块介绍3. 模块安装4. 代码实战4.1 英文图片测试4.2 数字图片测试4.3 中文图片识别 书籍分享 专栏导读 🔥🔥本文已收录于《100天精通Python从入门到就业》:本专栏专门针对零基础和需要进阶提升的同学所准…...

Go七天实现RPC
0.前言 本文是学习自7天用Go从零实现RPC框架GeeRPC | 极客兔兔 在此基础上,加入自己的学习过程与理解。 1.RPC 框架 RPC(Remote Procedure Call,远程过程调用)是一种计算机通信协议,允许调用不同进程空间的程序。RPC 的客户端和服务器可以…...
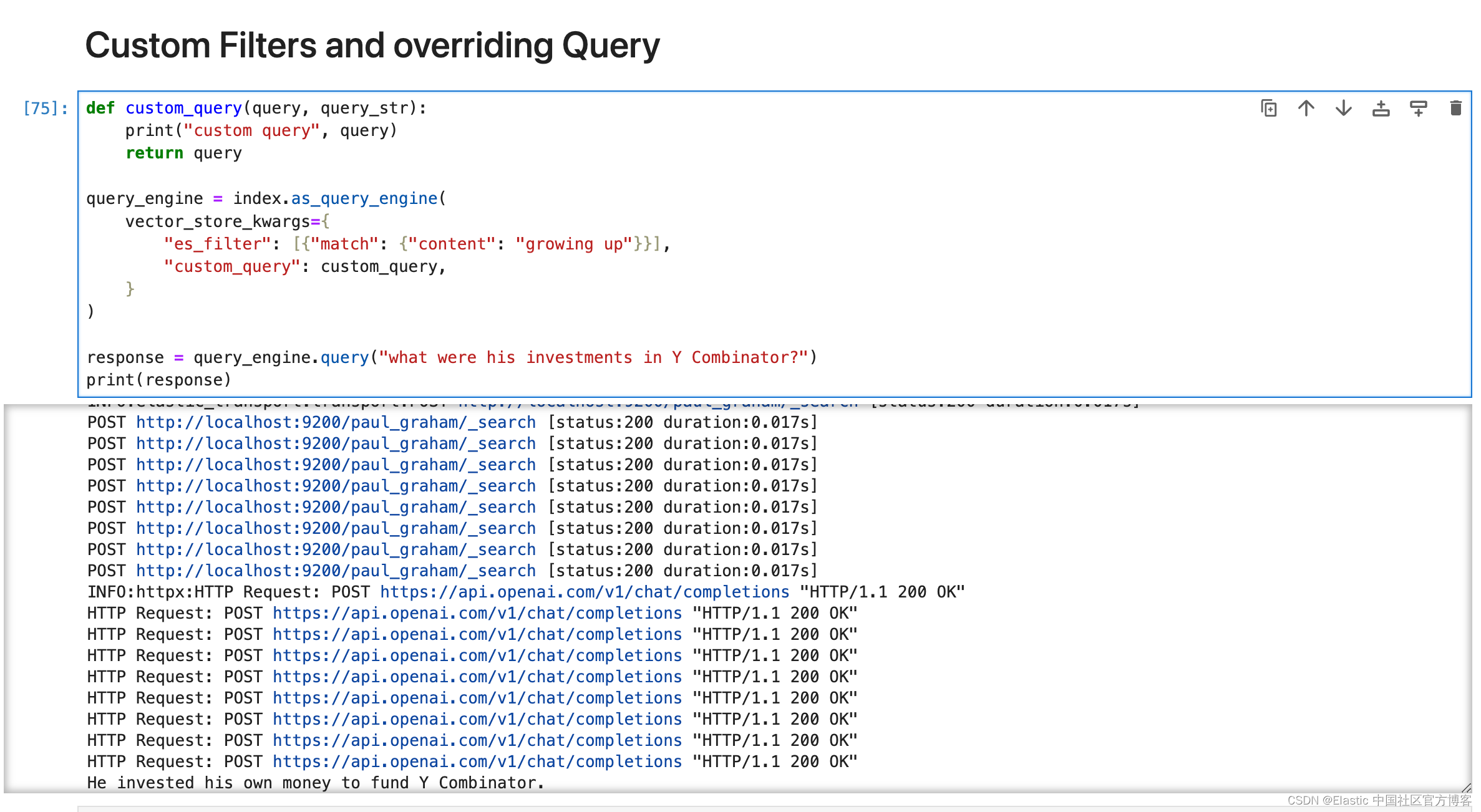
Elasticsearch:和 LIamaIndex 的集成
LlamaIndex 是一个数据框架,供 LLM 应用程序摄取、构建和访问私有或特定领域的数据。 LlamaIndex 是开源的,可用于构建各种应用程序。 在 GitHub 上查看该项目。 安装 在 Docker 上设置 Elasticsearch 使用以下 docker 命令启动单节点 Elasticsearch 实…...
QT操作office实例)
QT基础篇(14)QT操作office实例
1.QT操作office的基本方式 通过QT操作Office软件,可以使用Qt的QAxObject类来进行操作。下面是一个例子,展示了通过Qt操作Excel的基本方式: #include <QApplication> #include <QAxObject>int main(int argc, char *argv[]) {QA…...

重拾计网-第四弹 计算机网络性能指标
ps:本文章的图片内容来源都是来自于湖科大教书匠的视频,声明:仅供自己复习,里面加上了自己的理解 这里附上视频链接地址:1.5 计算机网络的性能指标(1)_哔哩哔哩_bilibili 目录 &#x…...
【Vue】Vue 路由的配置及使用
目录捏 前言一、路由是什么?1.前端路由2.后端路由 二、路由配置1.安装路由2.配置路由 三、路由使用1.route 与 router2. 声明式导航3. 指定组件的呈现位置 四、嵌套路由(多级路由)五、路由重定向1.什么是路由重定向?2.设置 redire…...

网络安全事件分级指南
一、特别重大网络安全事件 符合下列情形之一的,为特别重大网络安全事件: 1.重要网络和信息系统遭受特别严重的系统损失,造成系统大面积瘫痪,丧失业务处理能力。 2.国家秘密信息、重要敏感信息、重要数据丢失或被窃取、篡改、假…...

uniapp组件库SwipeAction 滑动操作 使用方法
目录 #平台差异说明 #基本使用 #修改按钮样式 #点击事件 #API #Props #Event 该组件一般用于左滑唤出操作菜单的场景,用的最多的是左滑删除操作。 注意 如果把该组件通过v-for用于左滑删除的列表,请保证循环的:key是一个唯一值,可以…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
