【C++进阶07】哈希表and哈希桶

一、哈希概念
顺序结构以及平衡树中
元素关键码与存储位置没有对应关系
因此查找一个元素
必须经过关键码的多次比较
顺序查找时间复杂度为O(N)
平衡树中为树的高度,即O( l o g 2 N log_2 N log2N)
搜索效率 = 搜索过程中元素的比较次数
理想的搜索方法:不经任何比较
一次直接从表中获取想要的元素
构造一种存储结构
通过某种函数(hashFunc)使元素的存储位置
与它的关键码之间建立一一映射的关系
就能在查找时通过该函数直接找到该元素
向该结构中:
插入元素:
根据待插入元素的关键码
以此函数计算出该元素的存储位置并按此位置
进行存放
搜索元素:
对元素的关键码进行同样的计算
把求得的函数值当做元素的存储位置
在结构中按此位置取元素比较
若关键码相等,则搜索成功
该方式即为:
哈希(散列)方法
哈希方法中使用的转换函数称为:
哈希(散列)函数
构造出来的结构称为:
哈希表(Hash Table)(或者称散列表)
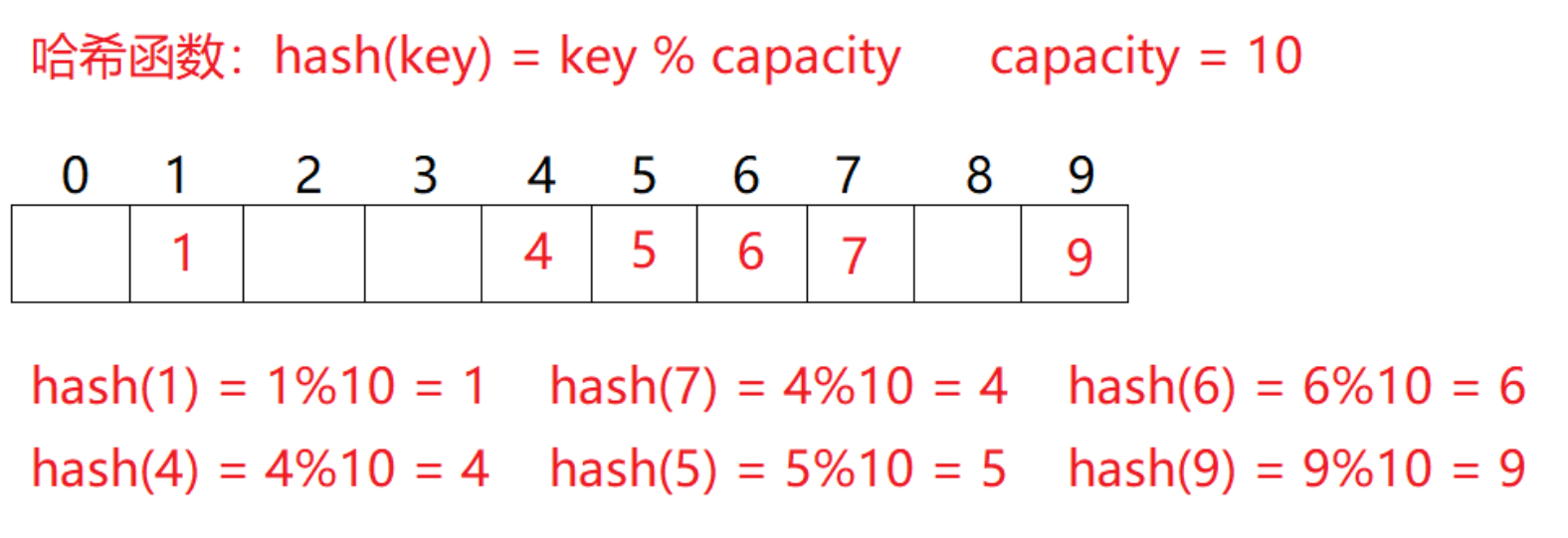
例如:
数据集合{1,7,6,4,5,9};
哈希函数设置为:
hash(key) = key % capacity;
capacity:
存储元素底层空间总的大小
二、哈希冲突
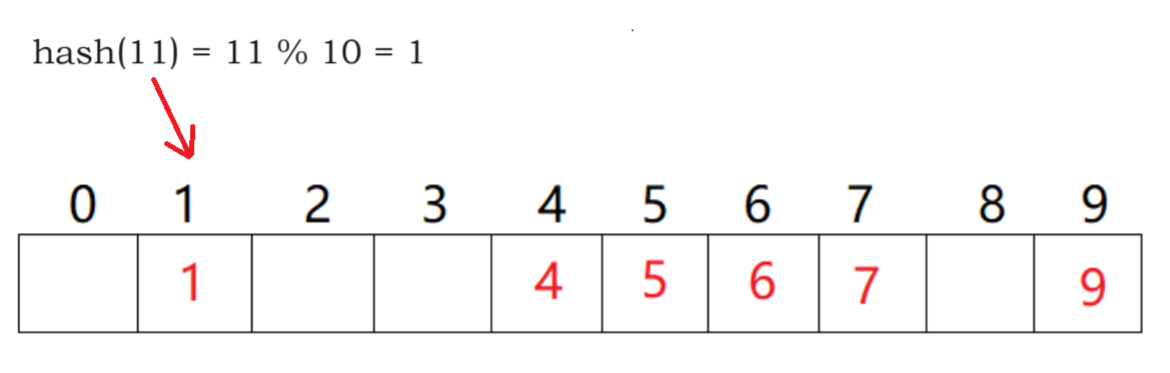
不同关键字通过相同的哈希函数
计算出相同的哈希地址
该种现象称为哈希冲突或哈希碰撞
把具有不同关键码
而具有相同哈希地址的数据元素称为“同义词”
11、21、31…数据经过哈希函数计算都为1
都插入在下标为1的地方便会冲突
三、哈希函数
引起哈希冲突的一个原因可能是:
哈希函数设计不够合理
哈希函数设计原则:
- 哈希函数的定义域必须包括
需要存储的全部关键码
而如果散列表允许有m个地址时
其值域必须在0到m-1之间 - 哈希函数计算出来的地址能均匀分布在
整个空间中 - 哈希函数应该比较简单
常用哈希函数:
-
直接定址法
取关键字的某个线性函数为散列地址:
Hash(Key)= A*Key + B
优点:简单、均匀
缺点:需要事先知道关键字的分布情况
使用场景:适合查找比较小且连续的情况
面试题:字符串中第一个只出现一次字符 -
除留余数法
设散列表中允许的地址数为m
取一个不大于m
但最接近或等于m的质数p作为除数
按照哈希函数:
Hash(key) = key% p(p<=m)
将关键码转换成哈希地址
四、哈希冲突解决
解决哈希冲突两种常见方法:
闭散列和开散列
4.1 闭散列
闭散列:也叫开放定址法
当发生哈希冲突时
如果哈希表未被装满
说明哈希表中必然还有空位置
那么可以把key存放到
冲突位置的“下一个” 空位置中去
那如何寻找下一个空位置呢?
- 线性探测
从发生冲突的位置开始
依次向后探测
直到寻找到下一个空位置为止
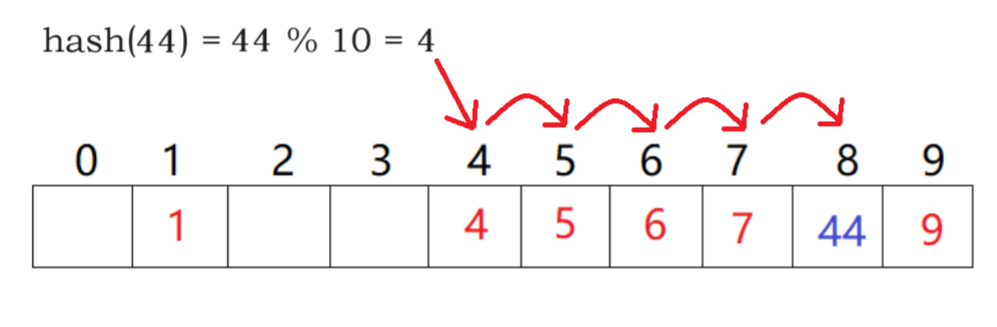
线性探测优点:实现简单
线性探测缺点:一旦发生哈希冲突
所有的冲突连在一起,容易产生数据“堆积”
即:不同关键码占据了可利用的空位置
使得寻找某关键码的位置需要许多次比较
导致搜索效率降低
- 二次探测
线性探测的缺陷是
产生冲突的数据堆积在一块
这与其找下一个空位置有关系
因为找空位置的方式就是挨着往后逐个去找
因此二次探测为了避免该问题
找下一个空位置的方法为:
H i H_i Hi = ( H 0 H_0 H0 + i 2 i^2 i2 )% m
或者: H i H_i Hi = ( H 0 H_0 H0 - i 2 i^2 i2 )% m
其中:i = 1,2,3…, H 0 H_0 H0是通过
散列函数Hash(x)对元素的关键码 key
进行计算得到的位置,m是表的大小
研究表明:当表的长度为质数且表装载因子
a不超过0.5时,新的表项一定能够插入
而且任何一个位置都不会被探查两次
因此只要表中有一半的空位置
就不会存在表满的问题
在搜索时可以不考虑表装满的情况
但在插入时必须确保表的装载因子a不超过
0.5,如果超出必须考虑增容
因此:比散列最大的缺陷就是空间利用率
比较低,这也是哈希的缺陷
4.2 开散列
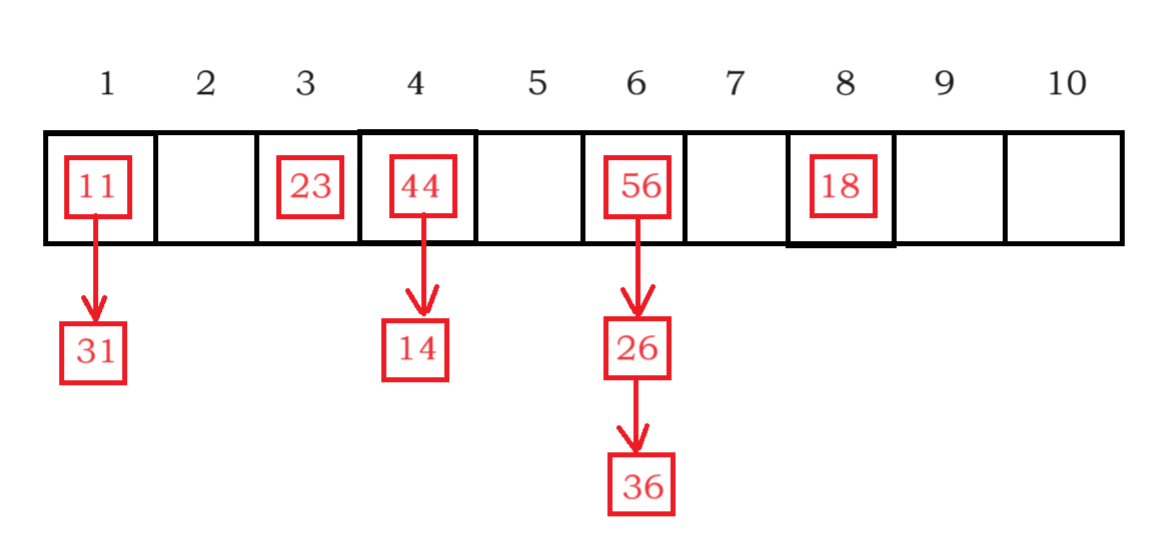
开散列法又叫链地址法(开链法)
首先对关键码集合用散列函数计算散列地址
具有相同地址的关键码归于同一子集合
每一个子集合称为一个桶
各个桶中的元素通过一个单链表链
接起来,各链表的头结点存储在哈希表中
如图:
将哈希地址相同的元素链接在同一个桶下面
在实际应用中
开散列比闭散列更实用
- 哈希桶负载因子更大
空间利用率高 - 极端情况也有解决方案
哈希桶极端情况:
所有元素在同一个桶
为了避免这种情况
当桶超过一定高度
将该桶转换为红黑树结构
五、哈希桶的模拟实现
5.1 基本框架
namespace HashBucket // 哈希桶
{ template <class K, class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next; // 单链表的方式链接HashNode(const pair<K, V>& kv): _next(nullptr), _kv(kv){}};template <class K, class V>class HashTable{typedef HashNode<K, V> Node;public:private:vector<Node*> _tables;size_t _n = 0; // 存储的有效数据个数 };
}
5.2 插入元素
哈希桶的增容
若哈希表的大小为0
将哈希表的初始值设置为10
若哈希表的负载因子等于1
创建一个新表,大小是原表的两倍
用新表的哈希函数计算旧表的每个
元素在新表的映射位置
将旧表的每个元素头插进新表
bool Insert(const pair<K, V>& kv)
{// 去重, 插入之前先查找有没有相同的元素if (Find(kv.first))return false;// 负载因子 == 1时扩容if (_n == _tables.size()){// 哈希表大小为0,将哈希表初始值设为10size_t newsize = _tables.size() == 0 ? 10 : _tables.size() * 2;vector<Node*> newtables(newsize, nullptr);for (auto& cur : _tables){while (cur) // current不为空, 把挂着的数据一个一个移到新表{Node* next = cur->_next;size_t hashi = cur->_kv.first % newtables.size();// 头插到新表cur->_next = newtables[hashi];newtables[hashi] = cur;cur = next;}}_tables.swap(newtables);}size_t hashi = kv.first % _tables.size();// 头插Node* newnode = new Node(kv);newnode->_next = _tables[hashi];_tables[hashi] = newnode;++_n;return true;
}Node* Find(const K& key)
{if (_tables.size() == 0)return nullptr;size_t hashi = key % _tables.size();Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){return cur;}cur = cur->_next;}return nullptr;
}bool Erase(const K& key)
{size_t hashi = key % _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key){if (prev == nullptr){_tables[hashi] = cur->_next;}else{prev->_next = cur->_next;}delete cur;return true;}else{prev = cur;cur = cur->_next;}}return false;
}
✨✨✨✨✨✨✨✨
本篇博客完,感谢阅读🌹
如有错误之处可评论指出
博主会耐心听取每条意见
✨✨✨✨✨✨✨✨
相关文章:

【C++进阶07】哈希表and哈希桶
一、哈希概念 顺序结构以及平衡树中 元素关键码与存储位置没有对应关系 因此查找一个元素 必须经过关键码的多次比较 顺序查找时间复杂度为O(N) 平衡树中为树的高度,即O( l o g 2 N log_2 N log2N) 搜索效率 搜索过程中元素的比较次数 理想的搜索方法:…...

Go 语言实现冒泡排序算法的简单示例
以下是使用 Go 语言实现冒泡排序算法的简单示例: package mainimport "fmt"func bubbleSort(arr []int) {n : len(arr)for i : 0; i < n-1; i {for j : 0; j < n-i-1; j {if arr[j] > arr[j1] {// 交换元素arr[j], arr[j1] arr[j1], arr[j]}}}…...
JAVA 学习 面试(五)IO篇
BIO是阻塞I/O,NIO是非阻塞I/O,AIO是异步I/O。BIO每个连接对应一个线程,NIO多个连接共享少量线程,AIO允许应用程序异步地处理多个操作。NIO,通过Selector,只需要一个线程便可以管理多个客户端连接࿰…...
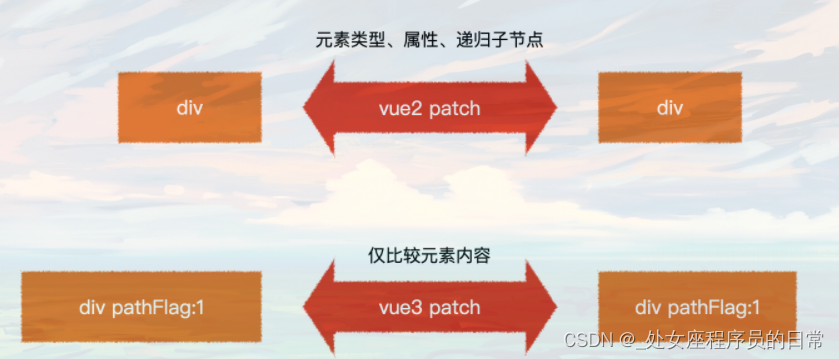
vue3相比vue2的效率提升
1、静态提升 2、预字符串化 3、缓存事件处理函数 4、Block Tree 5、PatchFlag 一、静态提升 在vue3中的app.vue文件如下: 在服务器中,template中的内容会变异成render渲染函数。 最终编译后的文件: 1.静态节点优化 那么这里为什么是两部分…...

web terminal - 如何在mac os上运行gotty
gotty可以让你使用web terminal的方式与环境进行交互,实现终端效果 假设你已经配置好了go环境,首先使用go get github.com/yudai/gotty命令获取可执行文件,默认会安装在$GOPATH/bin这个目录下,注意如果你的go版本比较高ÿ…...
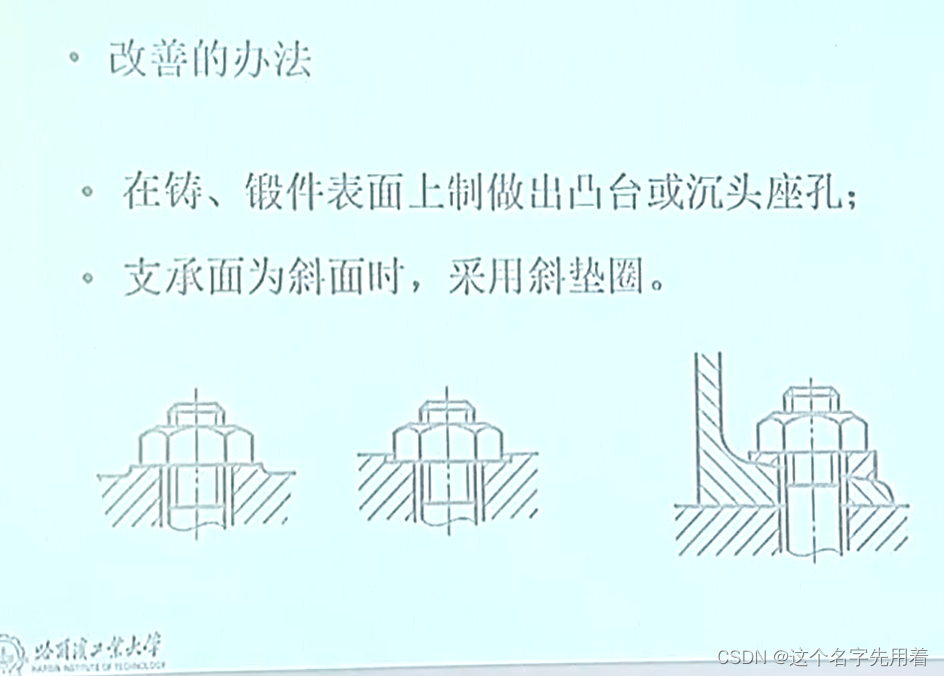
机械设计-哈工大课程学习-螺纹连接
圆柱螺纹主要几何参数螺纹参数 ①外径(大径),与外螺纹牙顶或内螺纹牙底相重合的假想圆柱体直径。螺纹的公称直径即大径。 ②内径(小径),与外螺纹牙底或内螺纹牙顶相重合的假想圆柱体直径。 ③中径ÿ…...

ai绘画|stable diffusion的发展史!简短易懂!!!
手把手教你入门绘图超强的AI绘画,用户只需要输入一段图片的文字描述,即可生成精美的绘画。给大家带来了全新保姆级教程资料包 (文末可获取) 一、stable diffusion的发展史 本文目标:学习交流 对于熟悉SD的同学&#x…...

水塘抽样算法
水塘抽样算法 1、问题描述 最近经常能看到面经中出现在大数据流中的随机抽样问题 即:当内存无法加载全部数据时,如何从包含未知大小的数据流中随机选取k个数据,并且要保证每个数据被抽取到的概率相等。 假设数据流含有N个数,我…...
easyui渲染隐藏域<input type=“hidden“ />为textbox可作为分割条使用
最近在修改前端代码的时候,偶然发现使用javascript代码渲染的方式将<input type"hidden" />渲染为textbox时,会显示一个神奇的效果,这个textbox输入框并不会隐藏,而是显示未一个细条,博主发现非常适合…...

100天精通Python(实用脚本篇)——第113天:基于Tesseract-OCR实现OCR图片文字识别实战
文章目录 专栏导读1. OCR技术介绍2. 模块介绍3. 模块安装4. 代码实战4.1 英文图片测试4.2 数字图片测试4.3 中文图片识别 书籍分享 专栏导读 🔥🔥本文已收录于《100天精通Python从入门到就业》:本专栏专门针对零基础和需要进阶提升的同学所准…...

Go七天实现RPC
0.前言 本文是学习自7天用Go从零实现RPC框架GeeRPC | 极客兔兔 在此基础上,加入自己的学习过程与理解。 1.RPC 框架 RPC(Remote Procedure Call,远程过程调用)是一种计算机通信协议,允许调用不同进程空间的程序。RPC 的客户端和服务器可以…...
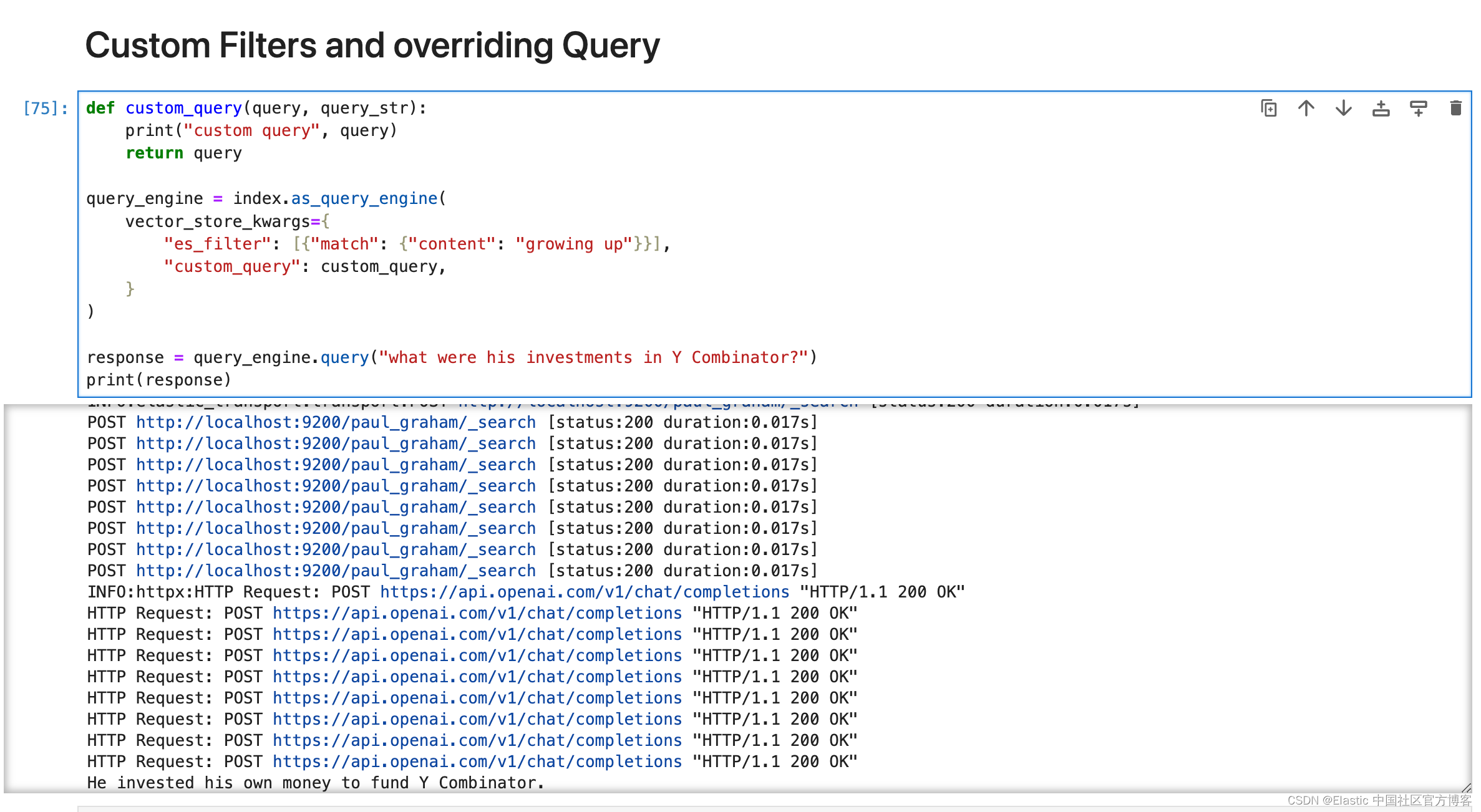
Elasticsearch:和 LIamaIndex 的集成
LlamaIndex 是一个数据框架,供 LLM 应用程序摄取、构建和访问私有或特定领域的数据。 LlamaIndex 是开源的,可用于构建各种应用程序。 在 GitHub 上查看该项目。 安装 在 Docker 上设置 Elasticsearch 使用以下 docker 命令启动单节点 Elasticsearch 实…...
QT操作office实例)
QT基础篇(14)QT操作office实例
1.QT操作office的基本方式 通过QT操作Office软件,可以使用Qt的QAxObject类来进行操作。下面是一个例子,展示了通过Qt操作Excel的基本方式: #include <QApplication> #include <QAxObject>int main(int argc, char *argv[]) {QA…...

重拾计网-第四弹 计算机网络性能指标
ps:本文章的图片内容来源都是来自于湖科大教书匠的视频,声明:仅供自己复习,里面加上了自己的理解 这里附上视频链接地址:1.5 计算机网络的性能指标(1)_哔哩哔哩_bilibili 目录 &#x…...
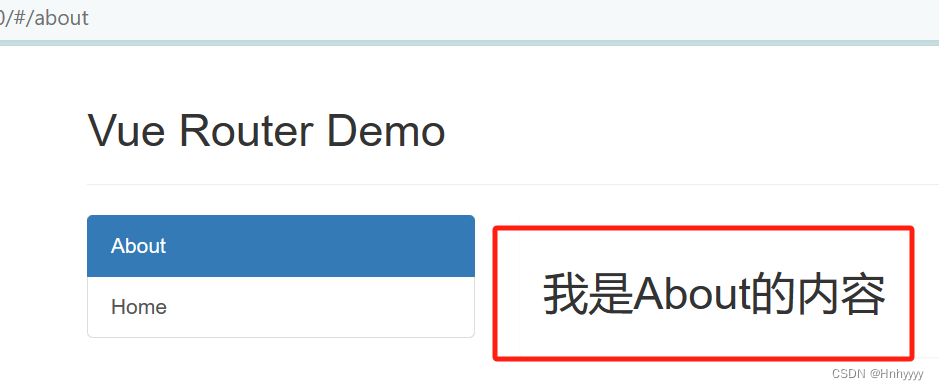
【Vue】Vue 路由的配置及使用
目录捏 前言一、路由是什么?1.前端路由2.后端路由 二、路由配置1.安装路由2.配置路由 三、路由使用1.route 与 router2. 声明式导航3. 指定组件的呈现位置 四、嵌套路由(多级路由)五、路由重定向1.什么是路由重定向?2.设置 redire…...

网络安全事件分级指南
一、特别重大网络安全事件 符合下列情形之一的,为特别重大网络安全事件: 1.重要网络和信息系统遭受特别严重的系统损失,造成系统大面积瘫痪,丧失业务处理能力。 2.国家秘密信息、重要敏感信息、重要数据丢失或被窃取、篡改、假…...

uniapp组件库SwipeAction 滑动操作 使用方法
目录 #平台差异说明 #基本使用 #修改按钮样式 #点击事件 #API #Props #Event 该组件一般用于左滑唤出操作菜单的场景,用的最多的是左滑删除操作。 注意 如果把该组件通过v-for用于左滑删除的列表,请保证循环的:key是一个唯一值,可以…...
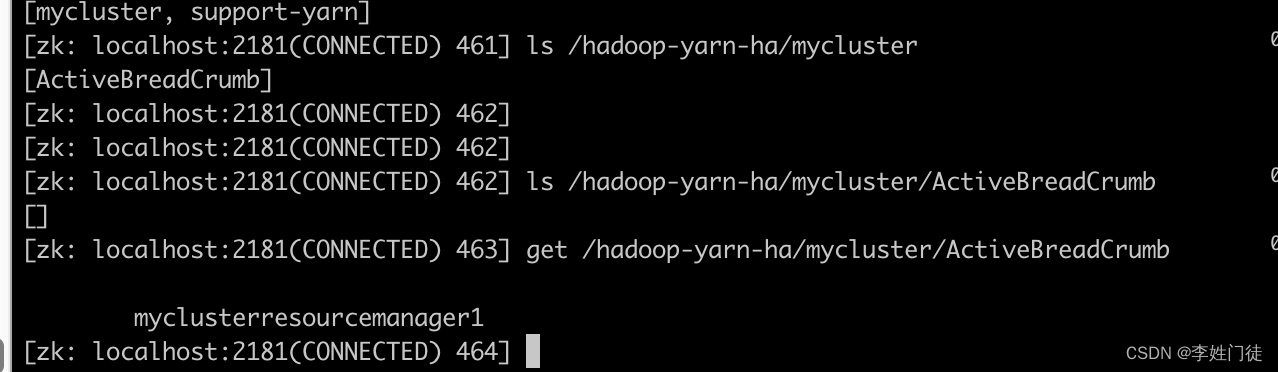
YARN节点故障的容错方案
YARN节点故障的容错方案 1. RM高可用1.1 选主和HA切换逻辑 2. NM高可用2.1 感知NM节点异常2.2 异常NM上的任务处理 4. 疑问和思考4,1 RM感知NM异常需要10min,对于app来说是否太长了? 5. 参考文档 本文主要探讨yarn集群的高可用容错方案和容错能力的探讨。…...

C++后端笔记
C后端笔记 资源整理一、高级语言程序设计1.1 进制1.2 程序结构基本知识1.3 数据类型ASCII码命名规则变量间的赋值浮点型变量的作用字符变量常变量 const运算符 二、高级语言程序设计(荣) 资源整理 C后端开发学习路线及推荐学习时间 C基础知识大全 C那…...

JavaEE中什么是Web容器?
Web容器(也称为Servlet引擎)是一个用于执行Java Servlet和JSP的服务器端环境。它负责管理和执行在其上运行的Web应用程序。 Tomcat是Web容器 Apache Tomcat 是一个流行的开源的Web容器,它实现了Java Servlet和JavaServer Pages(…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
