【学习】focal loss 损失函数
focal loss用于解决正负样本的不均衡情况
通常我们需要预测的正样本要少于负样本,正负样本分布不均衡会带来什么影响?主要是两个方面。
- 样本不均衡的话,训练是低效不充分的。因为困难的正样本数量较少,大部分时间都在学习没有用的负样本。
- 简单的负样本可能会压倒训练,导致训练退化。比如10000个人里面只有10个人为正义发声,其余的人都为邪恶发声,那么正义的声音就会被邪恶的声音淹没。
比如假如一张图片上有10个正样本,每个正样本的损失值是3,那么这些正样本的总损失是10x3=30。而假如该图片上有10000个简单易分负样本,尽管每个负样本的损失值很小,假设是0.1,那么这些简单易分负样本的总损失是10000x0.1=1000,那么损失值要远远高于正样本的损失值。所以如果在训练的过程中使用全部的正负样本,那么它的训练效果会很差。
focal loss的公式
首先看交叉熵损失函数:
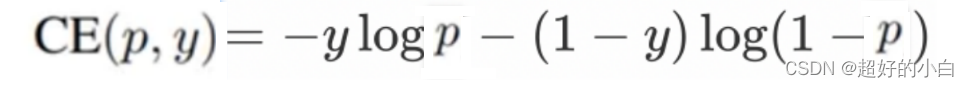
其中,y是样本的标签值,而p是模型预测某一个样本为正样本的概率,对于真实标签为正样本的样本,它的概率p越大说明模型预测的越准确,对于真实标签为负样本的样本,它的概率p越小说明模型预测的越准确,
上面公式可以变化如下:
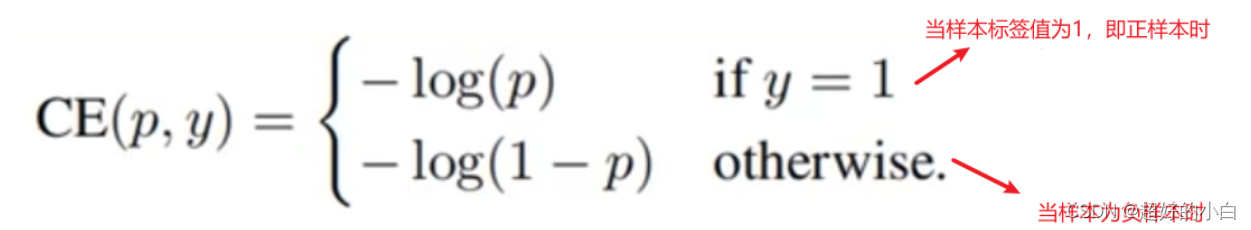
注意:这里的log(x)其实就是ln(x)
如果我们定义Pt 为如下形式:
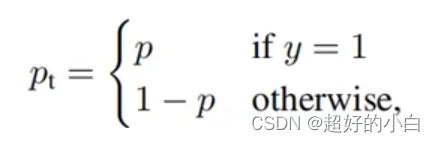
那么公式可以继续转化为:
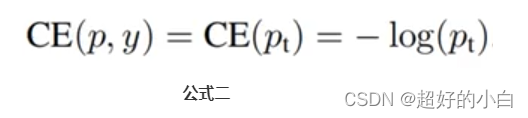
而对于focal loss来讲,就是要解决正负样本的权重问题。
focal loss 公式:
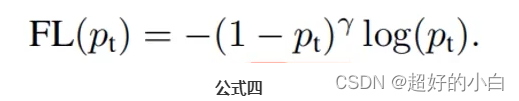
focal loss为什么起作用

参考b站:https://www.bilibili.com/video/BV1YX4y1J7Te/?spm_id_from=333.788&vd_source=4564794c2a933ffdf65d980ee25648f1
相关文章:

【学习】focal loss 损失函数
focal loss用于解决正负样本的不均衡情况 通常我们需要预测的正样本要少于负样本,正负样本分布不均衡会带来什么影响?主要是两个方面。 样本不均衡的话,训练是低效不充分的。因为困难的正样本数量较少,大部分时间都在学习没有用…...

几个好玩好用的AI站点
本文作者系360奇舞团前端开发工程师 ai能力在去年一年飞速增长,各种AI产品如雨后春笋般冒出来,在各种垂直领域上似乎都有AI的身影出现,今天就总结几款好玩的场景,看大家工作生活中是否会用到。 先说一个比较重要的消息是ÿ…...

Java算法 leetcode简单刷题记录5
Java算法 leetcode简单刷题记录5 老人的数目: https://leetcode.cn/problems/number-of-senior-citizens/ substring(a,b) 前闭后开 统计能整除数字的位数: https://leetcode.cn/problems/count-the-digits-that-divide-a-number/ 并不复杂,…...
计算机网络自顶向下Wireshark labs1-Intro
Wireshark labs1 实验文档:http://www-net.cs.umass.edu/wireshark-labs/Wireshark_Intro_v8.0.pdf 介绍 加深对网络协议的理解通常可以通过观察协议的运行和不断调试协议来大大加深,具体而言,就是观察两个协议实体之间交换的报文序列&…...

CSS实现图片放大缩小的几种方法
参考 方法一: 常用使用img标签,制定width或者height的任意一个,图片会自动等比例缩小 <div><img src"https://avatar.csdn.net/8/5/D/1_u012941315.jpg"/> </div> <!-- CSS--> <style> img {widt…...
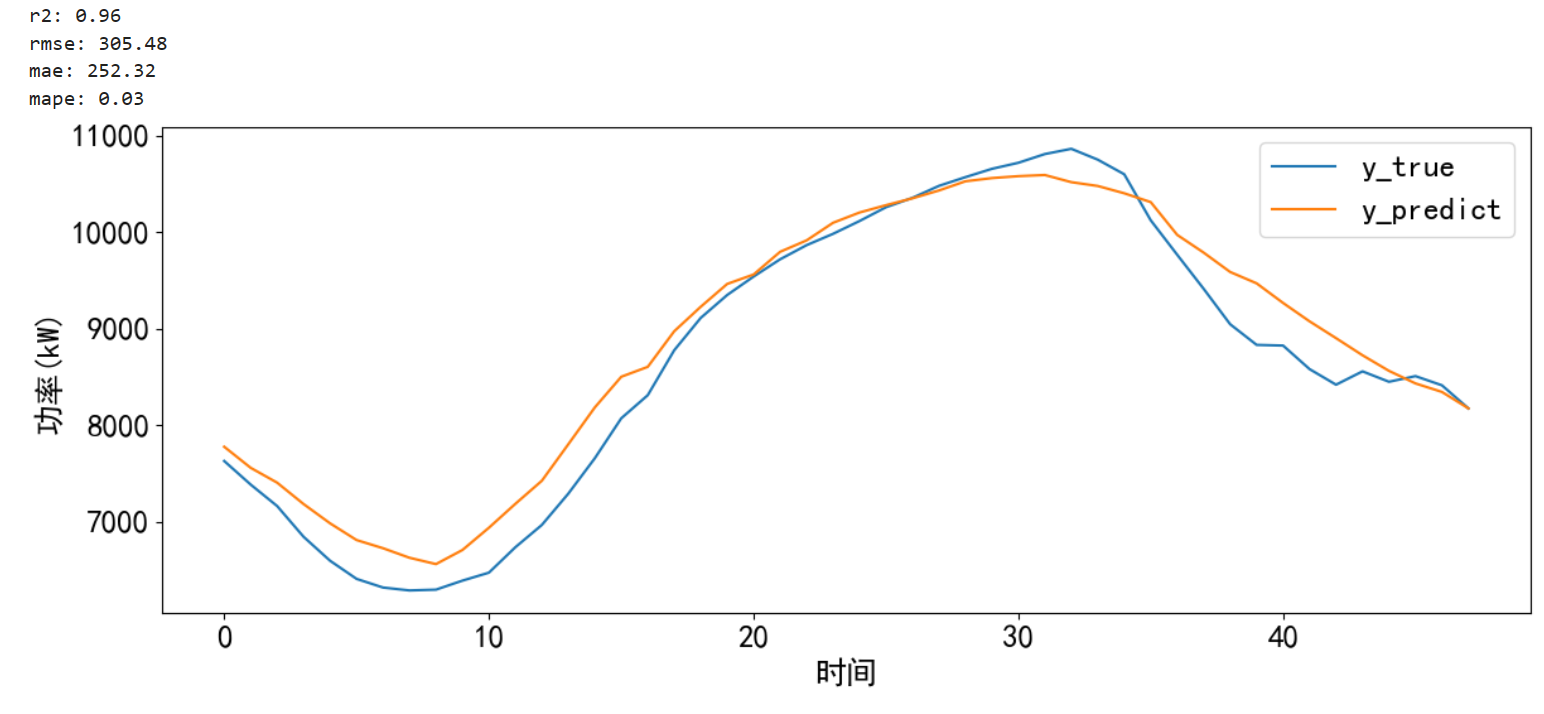
时间序列预测 — CNN-LSTM-Attention实现多变量负荷预测(Tensorflow):多变量滚动
专栏链接:https://blog.csdn.net/qq_41921826/category_12495091.html 专栏内容 所有文章提供源代码、数据集、效果可视化 文章多次上领域内容榜、每日必看榜单、全站综合热榜 时间序列预测存在的问题 现有的大量方法没有真正的预测未…...

angular-tree-component组件中实现特定节点自动展开
核心API 都在 expandToNode这个函数中 HTML treeData的数据结构大概如下 [{"key": "3293040275","id": "law_category/3293040275","name": "嘿嘿嘿嘿","rank": 0,"parentKey": "0&q…...

Linux系统下安装Vcpkg,并使用Vcpkg安装、编译OpenSceneGraph
环境:CentOS7 内存:8g(内存过少编译osg时会出现内存不足导致编译失败的情况,内存设置为4G时失败了,我直接加到了8g,所以就以8g为准了) 安装和配置vcpkg cd ~/ git clone https://www.github.com/microsoft/vcpkg cd …...
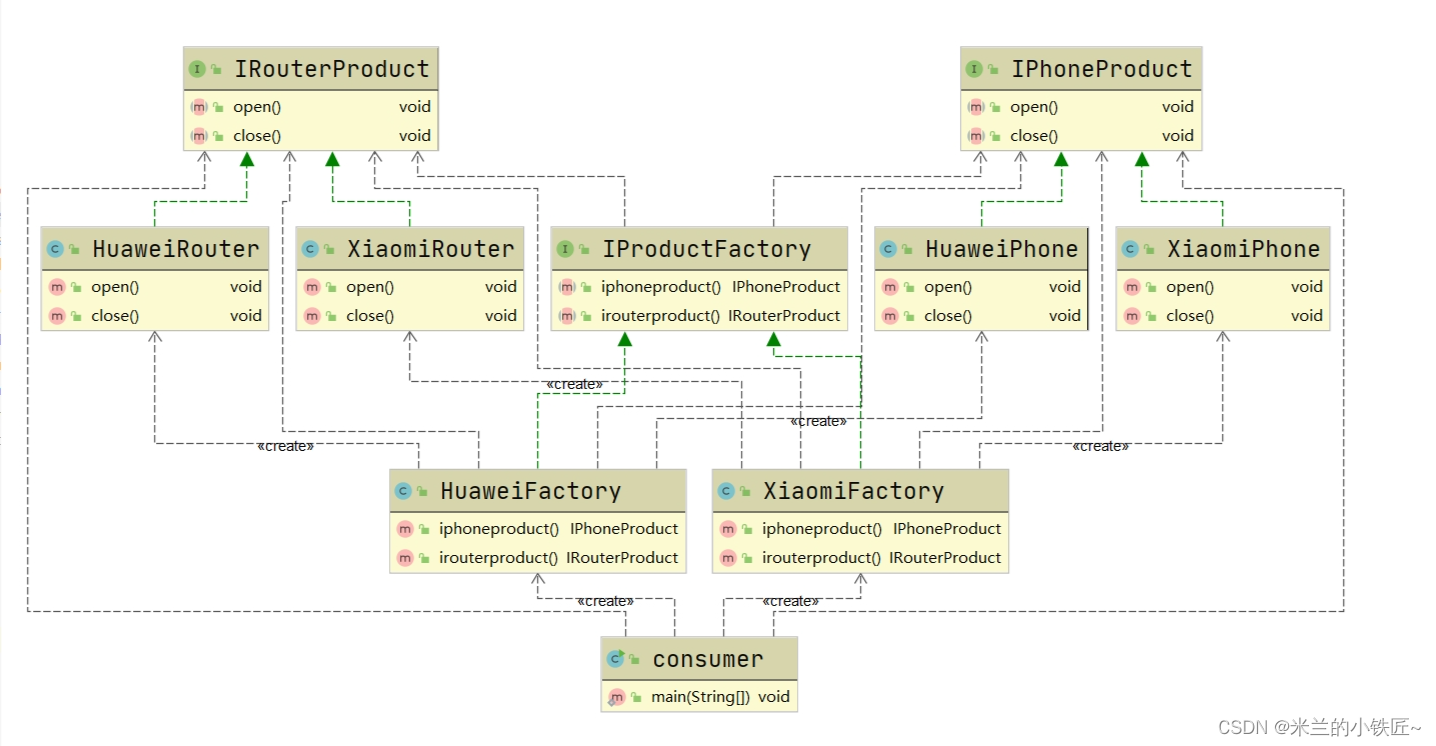
设计模式二(工厂模式)
本质:实例化对象不用new,用工厂代替,实现了创建者和调用者分离 满足: 开闭原则:对拓展开放,对修改关闭 依赖倒置原则:要针对接口编程 迪米特原则:最少了解原则,只与自己直…...

Maven应用手册
没加载出来就reimport,这个时候clean和install没用,那是编译安装项目的。 reimport干了什么? 结合idea的maven教程 父子模块 子模块不需要groupId ruoyi中父模块还添加了子模块的依赖,,, 先安装父再是子…...

笨蛋学设计模式行为型模式-状态模式【20】
行为型模式-状态模式 8.7状态模式8.7.1概念8.7.2场景8.7.3优势 / 劣势8.7.4状态模式可分为8.7.5状态模式8.7.6实战8.7.6.1题目描述8.7.6.2输入描述8.7.6.3输出描述8.7.6.4代码 8.7.7总结 8.7状态模式 8.7.1概念 状态模式是指对象在运行时可以根据内部状态的不同而改变它们…...
)
C++从零开始的打怪升级之路(day18)
这是关于一个普通双非本科大一学生的C的学习记录贴 在此前,我学了一点点C语言还有简单的数据结构,如果有小伙伴想和我一起学习的,可以私信我交流分享学习资料 那么开启正题 今天分享的是关于vector的题目 1.只出现一次的数字1 136. 只出…...

浅谈安科瑞直流电表在新加坡光伏系统中的应用
摘要:本文介绍了安科瑞直流电表在新加坡光伏系统中的应用。主要用于光伏系统中的电流电压电能的计量,配合分流器对发电量进行计量。 Abstract: This article introduces the application of Acrel DC meters in PV system in Indonesia.The device is …...
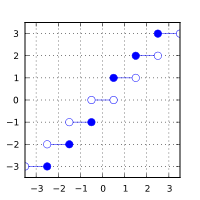
C++参悟:数值运算相关
数值运算相关 一、概述二、常用数学函数1. 基础运算1. 浮点值的绝对值( |x| )2. 浮点除法运算的余数3. 除法运算的有符号余数4. 除法运算的有符号余数和最后三个二进制位5. 混合的乘加运算6. 两个浮点值的较大者7. 两个浮点值的较小者8. 两个浮点值的正数…...

【Web前端开发基础】CSS的定位和装饰
CSS的定位和装饰 目录 CSS的定位和装饰一、学习目标二、文章内容2.1 定位2.1.1 定位的基本介绍2.1.2 定位的基本使用2.1.3 静态定位2.1.4 相对定位2.1.5 绝对定位2.1.6 子绝父相2.1.7 固定定位2.1.8元素的层级关系 2.2 装饰2.2.1 垂直对齐方式2.2.2 光标类型2.2.3 边框圆角2.2.…...
[pytorch入门] 3. torchvision中的transforms
torchvision中的transforms 是transforms.py工具箱,含有totensor、resize等工具 用于将特定格式的图片转换为想要的图片的结果,即用于图片变换 用法 在transforms中选择一个类创建对象,使用这个对象选择相应方法进行处理 能够选择的类 列…...
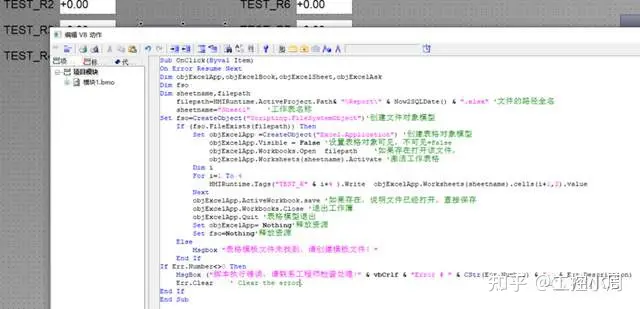
WINCC读写EXCEL-VBS
原创 RENHQ WINCC 关于VBS操作EXCEL的文档不管在论坛上还是在网上,相关的脚本已经很多,但是依然有很多人在问这个问题,于是把我以前在论坛上发的一个集合帖子的脚本拿来,重新开个帖子,如果再有人问的话,可…...

Python os模块
简介 Python的os模块是一个标准库模块,用于提供与操作系统相关的功能(相当于接口)。os模块允许Python程序与文件系统、目录结构、进程管理等操作系统级别的功能进行交互。 主要功能 文件和目录操作 创建、删除、重命名文件和目录…...

Elasticsearch:2023 年 Lucene 领域发生了什么?
作者:来自 Elastic Adrien Grand 2023 年刚刚结束,又是 Apache Lucene 开发活跃的一年。 让我们花点时间回顾一下去年的亮点。 社区 2023 年,有: 5 个次要版本(9.5、9.6、9.7、9.8 和 9.9),1 …...

Java算法 leetcode简单刷题记录4
Java算法 leetcode简单刷题记录4 买卖股票的最佳时机: https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/ 笨办法: 记录当天的值及之后的最大值,相减得到利润; 所有的天都计算下,比较得到利润最大值&…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
