数据结构与算法:二叉树专题
数据结构与算法:二叉树专题
- 前言
- 前提条件
- 基础知识
- 二叉树链式存储结构
- 二叉树中序遍历
- 二叉树层序遍历
- 常见编程题
- 把一个有序整数数组放到二叉树中
- 逐层打印二叉树结点数据
- 求一棵二叉树的最大子树和
- 判断两棵二叉树是否相等
- 把二叉树转换为双向链表
- 判断一个数组是否是二元查找树后序遍历的序列
- 找出排序二叉树上任意两个结点的最近共同父结点
- 复制二叉树
- 二叉树进行镜像反转
- 在二叉排序树中找出第一个大于中间值的结点
前言
- 本文是个人学习笔记,由于水平有限,难免出现错漏,敬请批评改正。
- 更多精彩内容,可点击进入数据结构与算法专栏或我的个人主页查看
前提条件
- 熟悉Python
- 熟悉数据结构与算法
基础知识
- 二叉树(BinaryTree)也称为二分树、二元树、对分树等,它是 n(n≥0)个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成。当集合为空时,称该二叉树为空二叉树。
- 在二叉树中,一个元素也称作一个结点。二叉树的递归定义为:二叉树或者是一棵空树,或者是一棵由一个根结点和两棵互不相交的分别称做根结点的左子树和右子树所组成的非空树,左子树和右子树又同样都是一棵二叉树。
- 二叉树的基本概念:
- (1)结点的度。结点所拥有的子树的个数称为该结点的度。
- (2)叶子结点。度为0的结点称为叶子结点,或者称为终端结点。
- (3)分支结点。度不为0的结点称为分支结点,或者称为非终端结点。一棵树的结点除叶子结点外,其余的都是分支结点。
- (4)左孩子、右孩子、双亲。树中一个结点的子树的根结点称为这个结点的孩子。这个结点称为它孩子结点的双亲。具有同一个双亲的孩子结点互称为兄弟。
- (5)路径、路径长度。如果一棵树的一串结点 n1,n2,…,nk 有如下关系:结点 ni 是 ni+1的父结点(1≤i≤k),就把n1,n2,…,nk称为一条由n1到nk的路径,长度是k-1。
- (6)祖先、子孙。在树中,如果有一条路径从结点M到结点N,那么M就称为N的祖先,而N称为M的子孙。
- (7)结点的层数。规定树的根结点的层数为1,其余结点的层数等于它的双亲结点的层数加1。
- (8)树的深度。树中所有结点的最大层数称为树的深度。
- (9)树的度。树中各结点度的最大值称为该树的度,叶子结点的度为0。
- (10)满二叉树。在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子结点都在同一层上,这样的一棵二叉树称作满二叉树。
- 完全二叉树。一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。完全二叉树的特点是:叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。需要注意的是满二叉树肯定是完全二叉树,而完全二叉树不一定是满二叉树。
- 二叉树的基本性质如下所示:
- 性质1:一棵非空二叉树的第i层上最多有2i−12^{i-1}2i−1个结点(i≥1)。
- 性质2:一棵深度为k的二叉树中,最多具有2k−12^{k}-12k−1个结点,最少有k个结点。
- 性质3:对于一棵非空的二叉树,度为0的结点(即叶子结点)总是比度为2的结点多一个,即如果叶子结点数为 n0,度数为 2的结点数为 n2,则有 n0=n2+1。
- 性质4:具有n个结点的完全二叉树的深度为「log2n」+1「log_2n」+1「log2n」+1。
- 性质5:对于具有n个结点的完全二叉树,如果按照从上至下和从左到右的顺序对二叉树中的所有结点从1开始顺序编号,则对于任意的序号为i的结点,有:
- (1)如果i>1,则序号为i的结点的双亲结点的序号为i/2(“/”表示整除);如果i=1,则序号为i的结点是根结点,无双亲结点。
- (2)如果2i≤n,则序号为i的结点的左孩子结点的序号为2i;如果2i>n,则序号为i的结点无左孩子。
- (3)如果2i+1≤n,则序号为i的结点的右孩子结点的序号为2i+1;如果2i+1>n,则序号为i的结点无右孩子。
- 此外,若对二叉树的根结点从0开始编号,则相应的i号结点的双亲结点的编号为(i-1)/2,左孩子的编号为2i+1,右孩子的编号为2i+2。
二叉树链式存储结构
class BiTNode:def __init__(self):self.data = Noneself.lchild = Noneself.rchild = None
二叉树中序遍历
# 用中序遍历的方式打印出二叉树结点的内容
def printTreeMidOrdel(root):if root ==None:returnif root.lchild!=None:printTreeMidOrdel(root.lchild)print(root.data,end=" ")if root.rchild!=None:printTreeMidOrdel(root.rchild)
二叉树层序遍历
def printTreeLayer(root):if root ==None:returnqueue = deque()queue.append(root)while len(queue)>0:p = queue.popleft()print(p.data,end=" ")if p.lchild !=None:queue.append(p.lchild)if p.rchild !=None:queue.append(p.rchild)
常见编程题
把一个有序整数数组放到二叉树中
- 题目:把一个有序的整数数组放到二叉树中。
- 实现思路:首先取数组的中间结点作为二叉树的根结点,把数组分成左右两部分,然后对于数组的左右两部分子数组分别运用同样的方法进行二叉树的构建,例如,对于左半部分子数组,取中间结点作为树的根结点,再把子数组分成左右两部分。依此类推,就可以完成二叉树的构建。
# 把有序数组转换为二叉树
def array2tree(arr,start,end):root = Noneif end>=start:root = BiTNode()mid = (start+end+1)//2# print(mid)# 树的根结点为数组中间的元素root.data = arr[mid]# 递归的用左半部分数组构造 root 的左子树root.lchild = array2tree(arr,start,mid-1)# 递归的用右半部分数组构造 root 的右子树root.rchild = array2tree(arr,mid+1,end)else:root = Nonereturn rootif __name__ == "__main__":arr = [1,2,3,4,5,6,7,8,9,10]print("数组:",arr)root = array2tree(arr,0,len(arr)-1)print("数组转换成树的中序遍历:",end=" ")printTreeMidOrdel(root) # 只遍历了一次数组,时间复杂度为O(N),
数组: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
数组转换成树的中序遍历: 1 2 3 4 5 6 7 8 9 10
- 只遍历了一次数组,因此,算法的时间复杂度为O(N)。
逐层打印二叉树结点数据
- 题目:给定一棵二叉树,要求逐层打印二叉树结点的数据。
- 实现思路:要求在遍历 一个结点的同时记录下它的孩子结点的信息,然后按照这个记录的顺序来访问结点的数据,在实现的时候可以采用队列来存储当前遍历到的结点的孩子结点,从而实现二叉树的层序遍历。
from collections import deque
# 逐层打印二叉树结点数据,层次遍历,借助队列
def printTreeLayer(root):if root ==None:returnqueue = deque()# 树根结点进队列queue.append(root)while len(queue)>0:p = queue.popleft()# 访问当前结点print(p.data,end=" ")# 如果这个结点的左孩子不为空则入队列if p.lchild !=None:queue.append(p.lchild)# 如果这个结点的右孩子不为空则入队列if p.rchild !=None:queue.append(p.rchild)if __name__ == "__main__":arr = [1,2,3,4,5,6,7,8,9,10]print("数组: ",arr)# 有序数组放到二叉树中root = array2tree(arr,0,len(arr)-1)# 层序遍历print("逐层打印二叉树结点数据:",end=" ")printTreeLayer(root)
数组: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
逐层打印二叉树结点数据: 6 3 9 2 5 8 10 1 4 7
- 在二叉树的层序遍历过程中,对树中的各个结点只进行了一次访问,因此,时间复杂度为O(N),此外,这种方法还使用了队列来保存遍历的中间结点,所使用队列的大小取决于二叉树中每一层 中结点个数的最大值 。具有 N 个结点的完全二叉树的深度为 h=log2N+1h=log_2N+1h=log2N+1 。而深度为 h 的这一层最多的结点个数为 2h−1=n/22^{h-1}=n/22h−1=n/2 。 也就是说队列中可能的最多的结点个数为 N/2 。因此,这种算法的空间复杂度为O(N) 。
求一棵二叉树的最大子树和
- 题目:给定一棵二叉树,它的每个结点都是正整数或负整数,如何找到一棵子树,使得它所有结点的和最大?
- 实现思路:针对每棵子树,求出这棵子树中所有结点的和,然后从中找出最大值。恰好二叉树的后序遍历就能做到这一点。在对二叉树进行后序遍历的过程中,如果当前遍历的结点的值与其左右子树和的值相加的结果大于最大值,则更新最大值。
# 最大子树和,借助后序遍历
class Test:def __init__(self):self.maxSum = -2**31 # 定义一个maxSum,用于存储最大和def findMaxSubTree(self,root,maxRoot):if root==None:return 0# 求 root 左子树所有结点的和lmax = self.findMaxSubTree(root.lchild,maxRoot)# 求 root 右子树所有结点的和rmax = self.findMaxSubTree(root.rchild,maxRoot)sums = lmax+rmax+root.data# 以 root 为根的子树的和大于前面求出的最大值if sums > self.maxSum:self.maxSum = sumsmaxRoot.data = root.data# 返回以 root 为根结点的子树的所有结点的和return sumsif __name__ == "__main__":arr = [1,2,3,4,5,6,7,8,9,10]print("数组: ",arr)# 有序数组放到二叉树中root = array2tree(arr,0,len(arr)-1)# 层序遍历print("逐层打印二叉树结点数据:",end=" ")printTreeLayer(root) print()test = Test()maxRoot = BiTNode()test.findMaxSubTree(root,maxRoot)print("最大子树和:",test.maxSum)print("最大子树根结点:",maxRoot.data)
数组: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
逐层打印二叉树结点数据: 6 3 9 2 5 8 10 1 4 7
最大子树和: 55
最大子树根结点: 6
- 时间复杂度为O(N),其中, N为二叉树的结点个数。
判断两棵二叉树是否相等
- 题目:两棵二叉树相等是指这两棵二 叉树有着相同的结构 ,并且在相同位置上的结点有相同的值。如何判断两棵二叉树是否相等?
- 实现思路:两棵二叉树 root1 、 root2 相等,那么 root1 与 root2 结点 的值相同,同时它们的左右孩子也有着相同的结构,并且对应位置上结点的值相等,即 root1.data=root2.data , 并且 root1的左子树与 root2 的左子树相等, root1 的右子树与 root2 的 右子树相等。根据这个条件,可以使用递归算法实现。
## 判断两颗二叉树是否相等
def isEqual(root1,root2):if root1==None and root2==None:return Trueif root1!=None and root2==None:return Falseif root1==None and root2!=None:return Falseif root1.data == root2.data:return isEqual(root1.lchild,root2.lchild) and isEqual(root1.rchild,root2.rchild)else:return Falseif __name__ == "__main__":arr1 = [1,2,3,4,5,6,7,8,9,10]print("数组: ",arr)# 有序数组放到二叉树中root1 = array2tree(arr1,0,len(arr1)-1)arr2 = [1,2,3,4,5,6,7,8,9,10]# 有序数组放到二叉树中root2 = array2tree(arr,0,len(arr2)-1)equal=isEqual(root1,root2)if equal:print("两棵树相等")else:print("两棵树不相等")
数组: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
两棵树相等
- 只对两棵树进行了一次遍历,因此 ,时向复杂度为O(N)。此外,这种方法没有申请额外的存储空间 。
把二叉树转换为双向链表
- 题目:输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。(要求不能创建任何新的结点,只能调整结点的指向。)
- 实现思路:转换后的双向链表 中结点的顺序与二叉树的中序遍历的顺序相同,因此,可以对二叉树的中序遍历算法进行修改,通过在中序遍历的过程中修改结点的指向来转换成一个排序的双向链表。 假设当前遍历的结点为 root , root 的 左子树已经被转换为双向链表,使用两个变量 pHead 与 pEnd 分别指向链表的头结点与尾结点。 那么在遍历 root 结点的时候,只需要将 root 结点的 lchild (左)指 向 pEnd ,把pEnd的 rchild (右)指向 root;此时root 结点就被加入到双向链表里 了,因此, root 变成了双向链表的尾结点。对于所有的结点都可以通过同样的方法来修改结点的指向。因此 ,可以采用递归的方法来求解,在求解的时候需要特别注意递归的结束条件以及边界情况 (例如双向链表为空的时候) 。
# 二叉树转换为双向链表,中序遍历
class Test:def __init__(self):self.pHead = None # 双向链表头结点self.pEnd = None # 双向链表尾结点# 把二叉树转换为双向列表def inOrderBSTree(self,root):if root ==None:return# 转换 root 的左子树self.inOrderBSTree(root.lchild) root.lchild=self.pEnd # 使当前结点的左孩子指向双向链表中最后一个结点if None == self.pEnd: # 双向列表为空,当前遍历的结点为双向链表的头结点self.pHead=rootelse: # 使双向链表中最后一个结点的右孩子指向当前结点self.pEnd.rchild=rootself.pEnd=root # 将当前结点设为双向链表中最后一个结点# #转换 root 的右子树self.inOrderBSTree(root.rchild)if __name__=="__main__":arr = [1,2,3,4,5,6,7]print("数组:",arr)test=Test()root = array2tree(arr,0,len(arr)-1)test.inOrderBSTree(root)print("转换后双向链表正向遍历:",end=' ')cur = test.pHeadwhile cur!=None:print(cur.data,end=' ')cur=cur.rchildprint()print("转换后双向链表逆向遍历:",end=' ')cur = test.pEndwhile cur!=None:print(cur.data,end=' ')cur=cur.lchild
数组: [1, 2, 3, 4, 5, 6, 7]
转换后双向链表正向遍历: 1 2 3 4 5 6 7
转换后双向链表逆向遍历: 7 6 5 4 3 2 1
- 二叉树的中序遍历有着相同的时间复杂度 O(N)。此外,这种方法只用了两个额外的变量 pHead 与 pEnd 来记录双向链表的首尾结点,因此,空间复杂度为 0(1)。
判断一个数组是否是二元查找树后序遍历的序列
- 题目:输入一个整数数组,判断该数组是否是某二元查找树的后序遍历的结果。如果是,那么返回 true ,否则返回 false 。
- 实现思路:二元查找树的特点是:对于任意一个结点,它的左子树上所有结点的值都小于这个结点的值,它的右子树上所有结点的值都大于这个结点的值。根据这个特点以及二元查找树后序遍历的特点,可以看出,这个序列的最后一个元素一定是树的根结点,然后在数组中找到第一个大于根结点的值,那么第一个大于根结点的结点之前的序列对应的结点一定位于根结点的左子树上,第一个大于根结点的结点(包含这个结点〉后面的序列一定位于根结点的右子树上,因此,可以通过递归方法来实现。
# 判断是否二元查找树的后序遍历
def IsAfterOrder(arr,start,end):if arr==None:return False# 数组的最后一个结点必定是根结点root = arr[end]# 找到第一个大于 root 的值,那么前面所有的结点都位于 root 的左子树上i=startwhile i<end:if arr[i]>root:breaki+=1# 如果序列是后续遍历的序列 , 那么从 i 开始的所有值都严该大于根结点 root 的值j=iwhile j<end:if arr[j]<root:return Falsej+=1left_IsAfterOrder=Trueright_IsAfterOrder=True# 判断小于 root 值的序列是否是某一二元查找树的后续遍历if i>start:left_IsAfterOrder=IsAfterOrder(arr,start,i-1)# 判断大于 root 值的序列是否是某一二元查找树的后续遍历if j<end:right_IsAfterOrder=IsAfterOrder(arr,i,end)return left_IsAfterOrder and right_IsAfterOrderif __name__=="__main__":
# arr = [1,2,3,4,5,6,7]arr = [1,3,2,5,7,6,4]print("数组:",arr)res = IsAfterOrder(arr,0,len(arr)-1)if res:print("是二元查找树的后序遍历")else:print("不是二元查找树的后序遍历")数组: [1, 3, 2, 5, 7, 6, 4]
是二元查找树的后序遍历
- 只对数组进行了一次遍历,因此,时间复杂度O(N)。
找出排序二叉树上任意两个结点的最近共同父结点
- 题目:对于一棵给定的排序二叉树, 求两个结点 的共同父结点。
- 实现思路:对于一棵二叉树的两个结点, 如果知道了从根结点到这两个结点的路径, 就可以很容易地找出它们最近的 公共父结点 。因此, 可以首先分别找出从根结点到这两个结点的路径,然后遍历这两条路径,只要是相等的结点都是它们的父结点,找到最后一个相等的结点即为离它们最近的共同父结点。
# 任意两个结点的最近共同父结点
class stack:# 初始栈def __init__(self):self.items = []# 判断校是否为空def isEmpty(self):return len(self.items)==0# 返回校的大小def size(self):return len(self.items)# 返回栈顶元素def peek(self):if not self.isEmpty():return self.items[len(self.items)-1]else:return None# 出栈def pop(self):if len(self.items)>0:return self.items.pop()else:print("栈为空")return None# 入栈def push(self,item):self.items.append(item)# 获取二叉树从根结点 root 到 node 结点的路径
def getPathFromRoot(root,node,stack):if root==None:return Falseif root == node:stack.push(root)return True# 如果 node 结点在 root 结点的左子树或右子树上,那么 root 就是 node 的祖先结点,把它加到校里if getPathFromRoot(root.lchild,node,stack) or getPathFromRoot(root.rchild,node,stack):stack.push(root)return Truereturn False# 查找二叉树中两个结点最近的共同父结点
def FindParentNode(root,node1,node2):stack1 = stack() # 保存从 root 到 node1 的路径stack2 = stack() # 保存从 root 到 node2 的路径getPathFromRoot(root,node1,stack1) # 获取从 root 到 node !的路径getPathFromRoot(root,node2,stack2) # 获取从 root 到 node2 的路径commomParent = Noneprint("stack1:",[i.data for i in stack1.items])print("stack2:",[i.data for i in stack2.items])# 获取最近 node1 和 node2 的父结点while stack1.peek()==stack2.peek():commomParent = stack1.peek()stack1.pop()stack2.pop()return commomParentif __name__=="__main__":arr = [1,2,3,4,5,6,7,8,9,10]print("数组:",arr)root = array2tree(arr,0,len(arr)-1)node1=root.lchild.lchild.lchildnode2 = root.lchild.rchildres =Noneres=FindParentNode(root, node1, node2)if res!=None:print(str(node1.data)+"和"+str(node2.data)+"的最近公共父结点为:"+str(res.data))else:print("没有公共父结点")
数组: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
stack1: [1, 2, 3, 6]
stack2: [5, 3, 6]
1和5的最近公共父结点为:3
- 当获取二叉树从根结点 root 到 node 结点的路径时,最坏的情况就是把树中所有结点都遍历了一遍,这个操作的时间复杂度为O(N),再分别找出从根结点到两个结点的路径后,找它们最近的公共父结点的 时间 复杂度也为O(N),因此,这种方法的时间复杂度为O(N)。
- 此外,这种方法用战保存了从根结点到特定结点的路径,在最坏的情况下,这个路径包含了树中所有的结点,因此,空间复杂度也为O(N)。
复制二叉树
- 题目:给定一个二叉树根结点,复制该树,返回新建树的根结点 。
- 实现思路:用给定的二叉树的根结点 root 来构造新的 二叉树的方法为:首先创建新的结点 dupTree,然后根据 root 结点来构造 dupTree 结点(dupTree.data=root.data), 最后分别用 root 的左右子树来构造 dupTree 的左右子树 。 根据这个思路可以使用递归方式实现二叉树的复制。
# 复制二叉树
# 任意两个结点的最近共同父结点
def createDupTree(root):if root==None:return NonedupTree = BiTNode()dupTree.data=root.data# 复制左子树dupTree.lchild=createDupTree(root.lchild)# 复制左子树dupTree.rchild=createDupTree(root.rchild)return dupTreeif __name__=="__main__":arr = [1,2,3,4,5,6,7,8,9,10]print("数组:",arr)root1 = array2tree(arr,0,len(arr)-1)# root2 =root1root2 =createDupTree(root1)print("原始二叉树中序遍历:",end=" ")printTreeMidOrdel(root1)print()print("复制二叉树中序遍历:",end=" ")printTreeMidOrdel(root2)
数组: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
原始二叉树中序遍历: 1 2 3 4 5 6 7 8 9 10
复制二叉树中序遍历: 1 2 3 4 5 6 7 8 9 10
- 对给定的二叉树进行了一次遍历,因此,时间复杂度为0(N),此外,这种方法需要申请N个额外的存储空间来存储新的二叉树 。
二叉树进行镜像反转
- 题目:二叉树的镜像就是二叉树对称的二叉树就是交换每一个非叶子结点的左子树指针和右子树指针。(注意 : 请勿对该树做任何假设,它不一定是平衡树 ,也不一定有序。)
- 实现思路:要实现二叉树的镜像反转,只需交换二叉树中所有结点的左右孩子即可。由于对所有的结点都做了同样的操作,因此,可以用递归的方法来实现。
# 二叉树镜像反转
def reverseTree(root):if root ==None:returnreverseTree(root.lchild)reverseTree(root.rchild)tmp= root.lchildroot.lchild=root.rchildroot.rchild =tmpif __name__ == "__main__":arr = [1,2,3,4,5,6,7]print("数组: ",arr)# 有序数组放到二叉树中root = array2tree(arr,0,len(arr)-1)# 层序遍历print("原始二叉树层序遍历:",end=" ")printTreeLayer(root)reverseTree(root)print()print("翻转二叉树层序遍历:",end=" ")printTreeLayer(root)
数组: [1, 2, 3, 4, 5, 6, 7]
原始二叉树层序遍历: 4 2 6 1 3 5 7
翻转二叉树层序遍历: 4 6 2 7 5 3 1
- 对二叉树进行了一次遍历, 因此,时间复杂度为O(N)。
在二叉排序树中找出第一个大于中间值的结点
- 题目:对于一棵二叉排序树 , 令mid=(最大值+最小值)/2 , 设计一个算法,找出距离mid值最近、大于mid值的结点 。
- 实现思路:首先需要找出二叉排序树中的最大值与最小值。由于二叉排序树的特点是:对于任意一个结点 ,它的左子树上所有结点的值都小于这个结点的值,它的右子树上所有结点的值都大于这个结点的值。因此,在二叉排序树中,最小值一定是最左下的结点,最大值一定是最右下的结点。根据最大值与最小值很容易就可以求出mid的值。接着,对二叉树进行中序遍历。如果当前结点的值小于mid,那么在这个结点的右子树中接着遍历,否则遍历这个结点的左子树。
# 查找值最小的 结点
def getMinNode(root):if root==None:return rootwhile root.lchild!=None:root=root.lchildreturn root# 查找值最大的结点
def getMaxNode(root):if root==None:return rootwhile root.rchild!=None:root=root.rchildreturn rootdef getNode(root):maxNode=getMaxNode(root)minNode=getMinNode(root)mid=(maxNode.data+minNode.data)/2res = Nonewhile root!=None:# 当前结点的值不大于mid则在右子树上找if root.data<=mid:root=root.rchildelse: # 在左子树上找res = rootroot=root.lchildreturn resif __name__ == "__main__":arr = [1,2,3,4,5,6,7]print("数组: ",arr)# 有序数组放到二叉树中root = array2tree(arr,0,len(arr)-1)print("第一个大于中间值的结点",getNode(root).data)
数组: [1, 2, 3, 4, 5, 6, 7]
第一个大于中间值的结点 5
- 在查找最大结点与最小结点时的时间复杂度为O(h), h为二叉树的高度 ,对于有N个结点的二叉排序树,最大的高度为O(N),最小的高度为 O(log2N)O(log_2N)O(log2N)。同理,在查找满足条件的结点的时候,时间复杂度也是O(h)。综上所述,这种方法的时间复杂度在最好的情况下是O(logN),最坏的情况下为O(N) 。
- 更多精彩内容,可点击进入数据结构与算法专栏或我的个人主页查看
相关文章:

数据结构与算法:二叉树专题
数据结构与算法:二叉树专题前言前提条件基础知识二叉树链式存储结构二叉树中序遍历二叉树层序遍历常见编程题把一个有序整数数组放到二叉树中逐层打印二叉树结点数据求一棵二叉树的最大子树和判断两棵二叉树是否相等把二叉树转换为双向链表判断一个数组是否是二元查…...

Cadence Allegro 导出Cadence Schematic Feedback Report详解
⏪《上一篇》 🏡《总目录》 ⏩《下一篇》 目录 1,概述2,Cadence Schematic Feedback Report作用3,Cadence Schematic Feedback Report示例4,Cadence Schematic Feedback Report导出方法4.1,方法1,4.2,方法2,...

《计算机系统基础》—— 运算
文章目录《计算机系统基础》——运算整数按位运算作用操作位移运算作用操作乘法运算除法运算浮点数加减运算乘除运算《计算机系统基础》——运算 🚀🚀本章我们需要介绍的是有关C语言里面的运算,当然了,我们不会是介绍简单的运算&…...

MSTP多进程讲解与实验配置
目录 MSTP多进程 专业术语 MSTP多进程配置 在MSTP域配置 MSTP多进程 多进程的作用 将设备上的端口绑定到不同的进程中,以进程为单位进行MSTP计算,不在同一进程内的端口不参与此进程中的MSTP协议计算,实现各个进程之间的生成树计算相互独立…...

【Python】软件测试必备:了解 fixture 在自动化测试中的重要作用
在自动化软件测试中,fixture 是一种确保测试在一致且受控条件下运行的重要方法。简单来说,fixture 就是一组先决条件或固定状态,必须在运行一组测试之前建立。在测试框架中,fixture 提供了一种方便的方法,用于在每个测…...

DevExpress皮肤引用的办法
1.引用Dll皮肤文件Typeprocedure SetSkin(skinnam:string);procedure TFrmMain.SetSkin(skinnam:string);varHinst:THANDLE;RStream:TResourceStream;beginHinst:Loadlibrary(ALLSK.dll);If Hinst0 ThenExitelsebeginRstream:TResourceStream.Create(Hinst,skinnam,MYSKIN);dxS…...

2023-03-04 区分纳米颗粒核壳原子
声明:未经允许,不得擅自复制、转载。欢迎引用:Laser-Assisted Synthesis of Bi-Decorated Pt Aerogel for Efficient Methanol Oxidation ElectrocatalysisApplied Surface Science ( IF 6.707 ) Pub Date : 2022-04-01 , DOI: 10.1016/j.aps…...

review设备管理
目录 1、设备管理基础知识 (1)、外部设备分类 (2)、注意事项 2、I/O硬件原理 (1)、不同方式对I/O设备分类 (2)、I/O控制方式 (3)、设备控制器 3、I/O软…...
详解)
Cadence Allegro 导出Bill of Material Report (Condensed)详解
⏪《上一篇》 🏡《总目录》 ⏩《下一篇》 目录 1,概述2,Bill of Material Report (Condensed)作用3,Bill of Material Report (Condensed)示例4,Bill of Material Report (Condensed)导出方法4.1,方法14.2,方法2,...

B. Sherlock and his girlfriend
Sherlock has a new girlfriend (so unlike him!). Valentines day is coming and he wants to gift her some jewelry. He bought n pieces of jewelry. The i-th piece has price equal to i 1, that is, the prices of the jewelry are 2, 3, 4, ... n 1. Watson…...

Spring SpEL表达式
Java知识点总结:想看的可以从这里进入 目录17、Spring SpEL17.1、简介17.2、配合value使用17.2.1、基本字面值17.2.2、类相关表达式17.2.3、properties17.2.4、T运算符17.2.5、new17.2.6、Elvis运算符17.2.7、运算符17.2、配合XML使用17、Spring SpEL 17.1、简介 S…...

Nginx反向代理原理详解与配置
Nginx反向代理是一种常用的反向代理技术,它允许您将一个或多个Web服务器上的内容公开给Internet上的客户端,而不必暴露您的服务器的IP地址。Nginx反向代理的原理是:客户端发出一个HTTP请求,Nginx服务器收到请求后,将请…...

Happen-Before从入门到踹门
什么是Happen-Before有人翻译为"先行发生原则",其实也没错,但是更准确的说法应该是,前一个操作的值,后一个总能察觉到。Happen-Before的八条规则程序有序性:在前面的代码优先于在后面的代码执行volatile的变…...

电力系统系统潮流分析【IEEE 57 节点】(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...
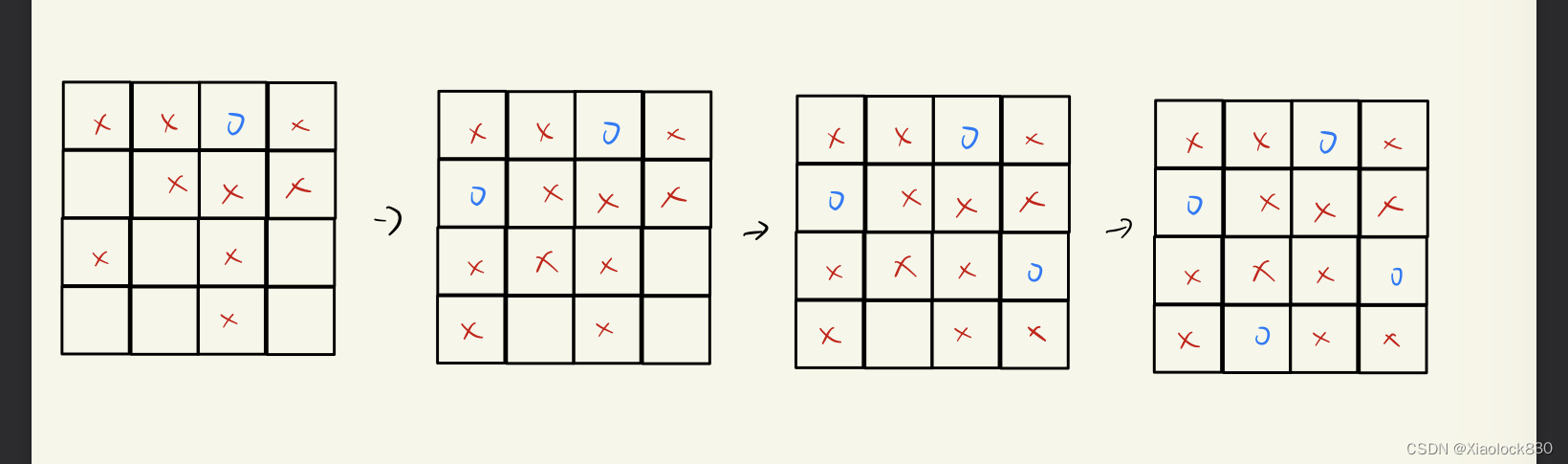
Java——N皇后问题
题目链接 leetcode在线oj题——N皇后 题目描述 按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题 研究的是如何将 n 个皇后放置在 nn 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ÿ…...
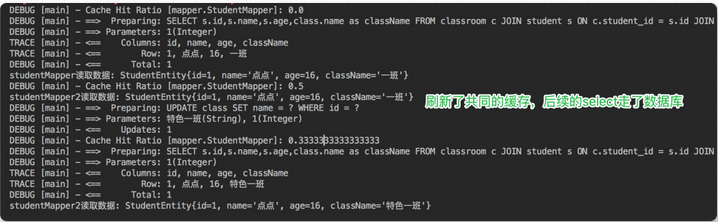
Mybatis一级缓存与二级缓存
一、MyBatis 缓存缓存就是内存中的数据,常常来自对数据库查询结果的保存。使用缓存,我们可以避免频繁与数据库进行交互,从而提高响应速度。MyBatis 也提供了对缓存的支持,分为一级缓存和二级缓存,来看下下面这张图&…...
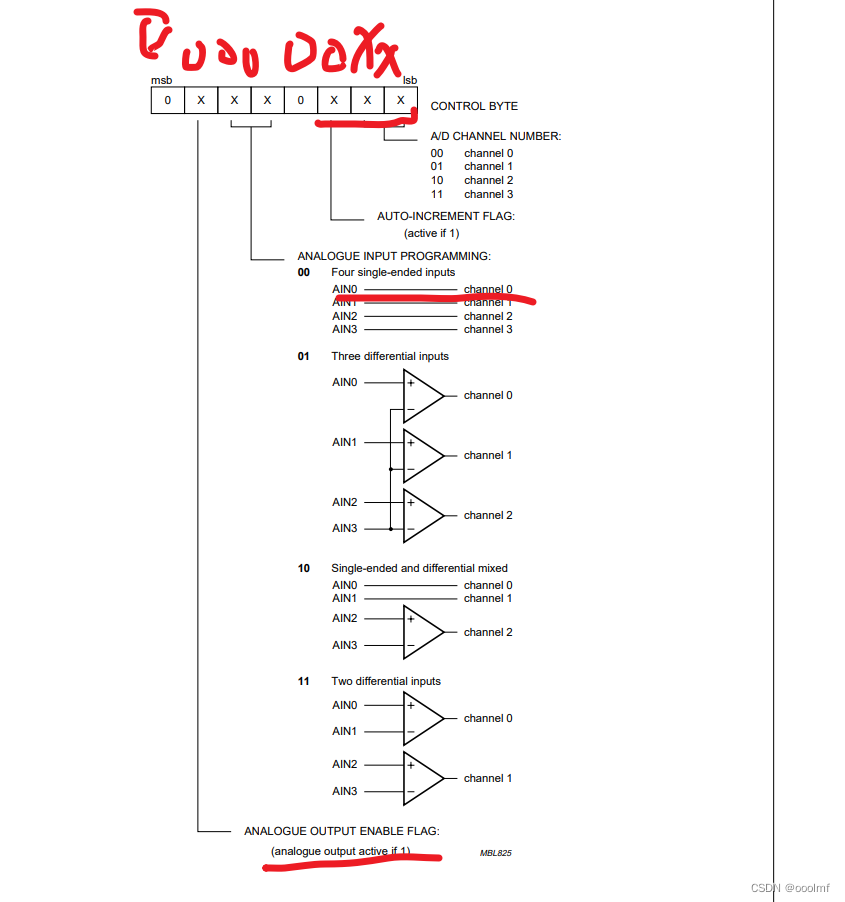
LQB,手打,PCF8591,ADDA转换,AD1是光敏电阻,AD3是电位器,DA输出
在上述at24c02de 基础上,添加三个函数 一个是读取通道1光敏电阻的数据; 一个是读取通道3的电压; 一个是输出DA的数据。。 5V的AD DA。 如果读入的电压是5V,输入AD,就是255; 如果是0V,就是00000…...

【计组笔记06】计算机组成与原理之控制器和总线结构
这篇文章,主要介绍计算机组成与原理之控制器和总线结构。 目录 一、控制器功能 1.1、控制器组成 1.2、控制单元的输入和输出...

elisp简单实例: auto-save
elisp 能找一个简单又实用的代码很不容易,以下代码不是我的原创,只是结合自己的理解,添加修正了一些注释,荣誉归原作者,感谢原作者的开源精神! 调用说明: 把后面代码存为auto-save.el 在init.el 中写上 (require auto-save) 就可以了. 下面是auto-save.el 内容了. ;; 我…...

写字楼/园区/购物中心空置率太高?快用快鲸智慧楼宇系统
客户租不租你的写字楼,事关区位、交通、环境、价格、面积、装修等诸多因素,但很多招商部对这些影响客户决策的数据并不重视,在客户初次上门看房时仅简单记录姓名、联系方式、需求面积,对其他核心数据熟视无睹,也为日后…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
