【腾讯云】您使用的腾讯云服务存在违规信息,请尽快处理
收到【腾讯云】您使用的腾讯云服务存在违规信息,请尽快处理,如何解决?在腾讯云服务器部署网站提示网站有违规信息如何处理?腾讯云百科txybk告诉各位站长,在腾讯网址安全中心申诉,申诉通过后截图上传给腾讯云客服即可解封。
腾讯云百科网在腾讯云服务器上部署的网站,突然收到腾讯云站内信,提示我的腾讯云服务存在违规信息,如下:
【腾讯云】您使用的腾讯云服务存在违规信息,请尽快处理
尊敬的腾讯云用户,您好!
您的腾讯云账号(账号ID: 10, 昵称: 腾讯云)下的CVM服务存在违规信息,请您第一时间完成违规信息处理,避免违规资源43.1.1.18被封禁,影响您的业务运营。感谢您的理解和支持!
违规URL:
违规域名:无
违规标识:
解决方法如下:
1、先检查你的违规URL,是否真的违规?如果违规了,请及时整改;
2、将确认非违规的URL,提交到腾讯安全-网址安全中心进行申诉,申诉链接https://urlsec.qq.com/complain.html
3、申诉成功后,将申诉成功的截图,通过提交工单的形式给腾讯云客服处理即可。
相关文章:

【腾讯云】您使用的腾讯云服务存在违规信息,请尽快处理
收到【腾讯云】您使用的腾讯云服务存在违规信息,请尽快处理,如何解决?在腾讯云服务器部署网站提示网站有违规信息如何处理?腾讯云百科txybk告诉各位站长,在腾讯网址安全中心申诉,申诉通过后截图上传给腾讯云…...
深度学习 Day27——J6ResNeXt-50实战解析
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 | 接辅导、项目定制🚀 文章来源:K同学的学习圈子 文章目录 前言1 我的环境2 pytorch实现DenseNet算法2.1 前期准备2.1.1 引入库2.1.2 设…...
 C++题解(数学+递归+快速幂))
【力扣 50】Pow(x, n) C++题解(数学+递归+快速幂)
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。 示例 1: 输入:x 2.00000, n 10 输出:1024.00000 示例 2: 输入:x 2.10000, n 3 输出:9.26100 …...

速盾:服务器接入CDN后上传图片失败的解决方案
本文将探讨当服务器接入CDN后,上传图片失败的常见原因,并提供解决方案以解决这些问题。同时,我们还将附上一些相关的问题和解答,让读者更好地理解和应对这些挑战。 随着互联网的持续发展,网站的性能和速度对于用户体验…...
LabVIEW高级CAN通信系统
LabVIEW高级CAN通信系统 在现代卫星通信和数据处理领域,精确的数据管理和控制系统是至关重要的。设计了一个基于LabVIEW的CAN通信系统,它结合了FPGA技术和LabVIEW软件,主要应用于模拟卫星平台的数据交换。这个系统的设计不仅充分体现了FPGA在…...
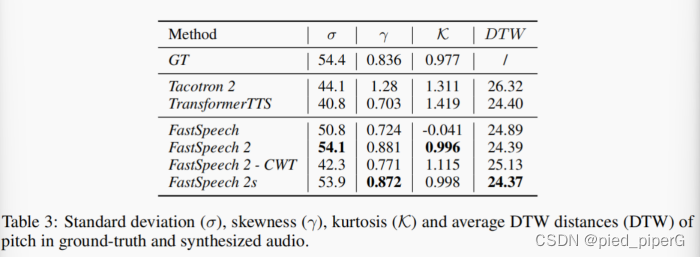
FastSpeech2——TTS论文阅读
笔记地址:https://flowus.cn/share/1683b50b-1469-4d57-bef0-7631d39ac8f0 【FlowUs 息流】FastSpeech2 论文地址:lFastSpeech 2: Fast and High-Quality End-to-End Text to Speechhttps://arxiv.org/abs/2006.04558 Abstract: tacotron→…...
如何才能拥有比特币 - 01 ?
如何才能拥有BTC 在拥有 BTC 之前我们要先搞明白 BTC到底保存在哪里?我的钱是存在银行卡里的,那我的BTC是存在哪里的呢? BTC到底在哪里? 一句话概括,BTC是存储在BTC地址中,而且地址是公开的,…...

Unity | 渡鸦避难所-8 | URP 中利用 Shader 实现角色受击闪白动画
1. 效果预览 当角色受到攻击时,为了增加游戏的视觉效果和反馈,可以添加粒子等动画,也可以使用 Shader 实现受击闪白动画:受到攻击时变为白色,逐渐恢复为正常颜色 本游戏中设定英雄受击时播放粒子效果,怪物…...

K8S--安装metrics-server,解决error: Metrics API not available问题
原文网址:K8S--安装metrics-server,解决error: Metrics API not available问题-CSDN博客 简介 本文介绍K8S通过安装metrics-server来解决error: Metrics API not available问题的方法。 Metrics Server采用了Kubernetes Metrics API的标准,…...

flume自定义拦截器
要自定义 Flume 拦截器,你需要编写一个实现 org.apache.flume.interceptor.Interceptor 接口的自定义拦截器类。以下是一个简单的示例: import org.apache.flume.Context; import org.apache.flume.Event; import org.apache.flume.interceptor.Interce…...
安卓Spinner文字看不清
Holo主题安卓13的Spinner文字看不清,明明已经解决了,又忘记了。 spinner.setOnItemSelectedListener(new Spinner.OnItemSelectedListener() {public void onItemSelected(AdapterView<?> arg0, View arg1, int arg2, long arg3) {TextView textV…...
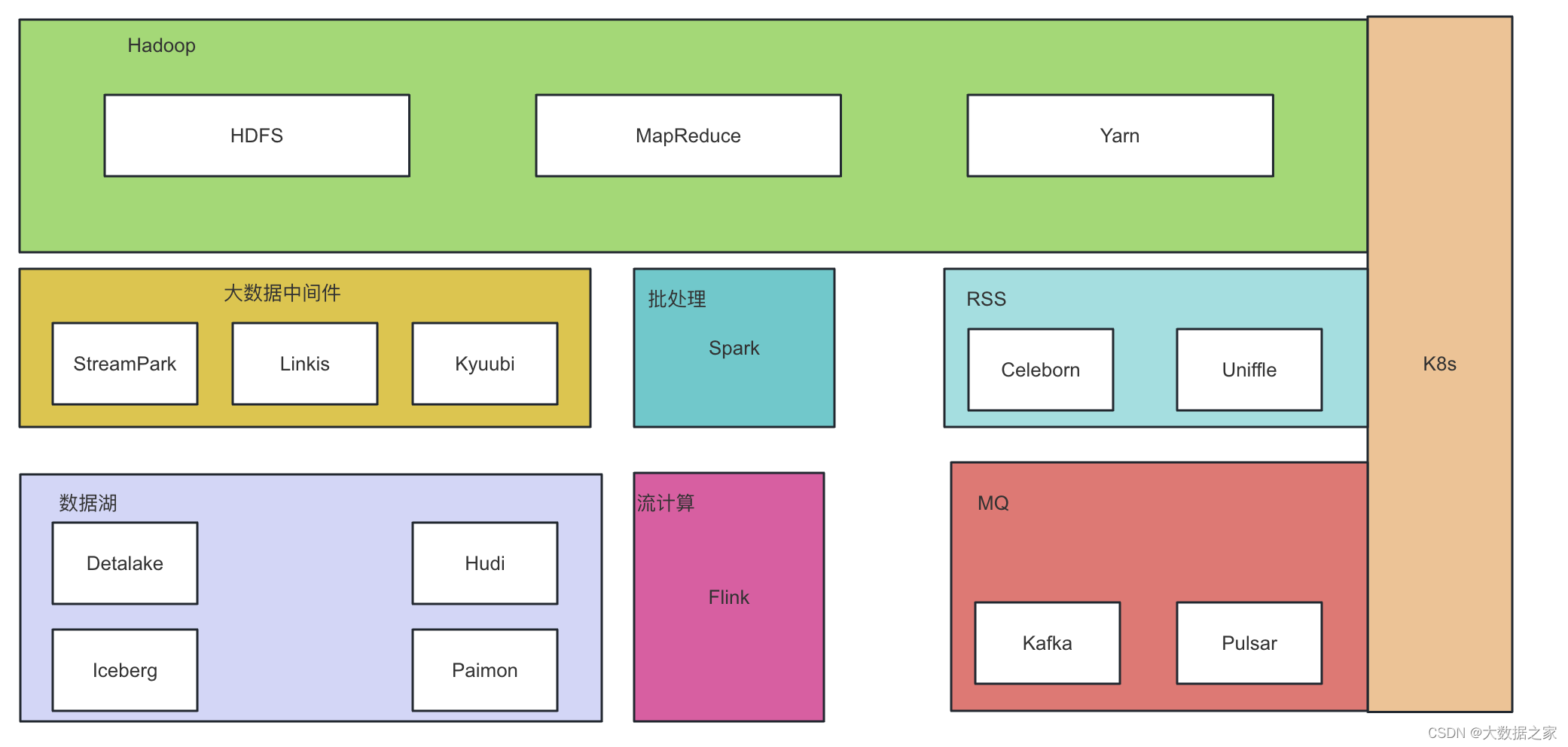
深入浅出hdfs-hadoop基本介绍
一、Hadoop基本介绍 hadoop最开始是起源于Apache Nutch项目,这个是由Doug Cutting开发的开源网络搜索引擎,这个项目刚开始的目标是为了更好的做搜索引擎,后来Google 发表了三篇未来持续影响大数据领域的三架马车论文: Google Fil…...
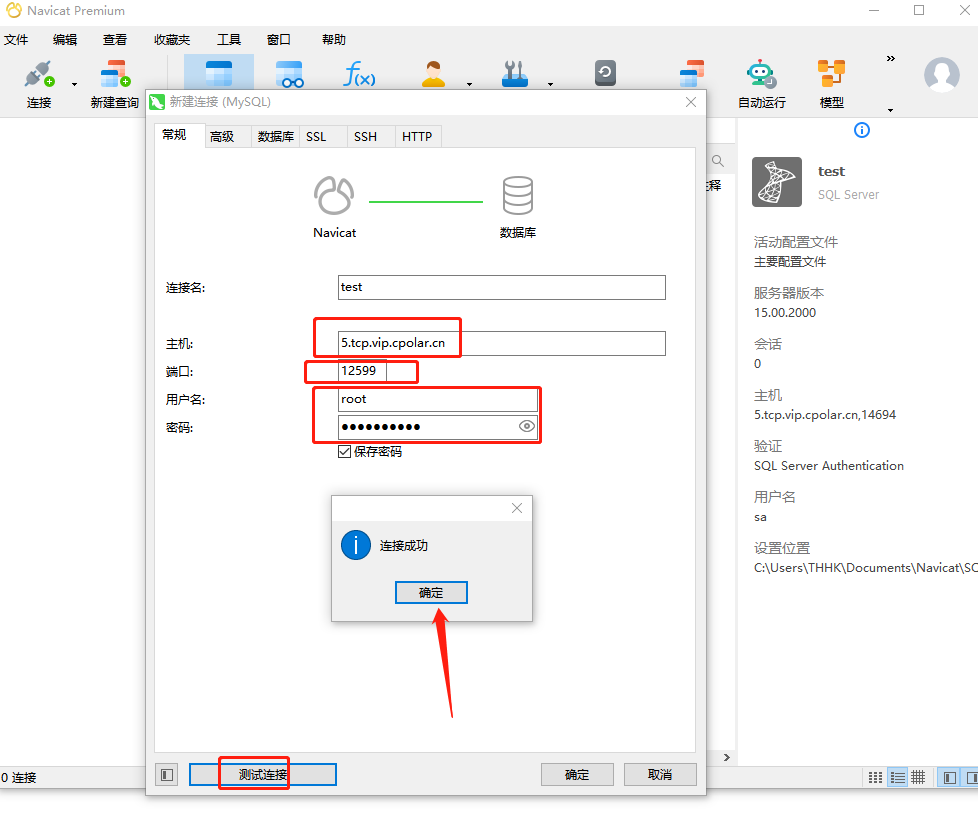
宝塔面板部署MySQL并结合内网穿透实现公网远程访问本地数据库
文章目录 前言1.Mysql服务安装2.创建数据库3.安装cpolar3.2 创建HTTP隧道 4.远程连接5.固定TCP地址5.1 保留一个固定的公网TCP端口地址5.2 配置固定公网TCP端口地址 前言 宝塔面板的简易操作性,使得运维难度降低,简化了Linux命令行进行繁琐的配置,下面简单几步,通过宝塔面板cp…...
数据结构<1>——树状数组
树状数组,也叫Fenwick Tree和BIT(Binary Indexed Tree),是一种支持单点修改和区间查询的,代码量小的数据结构。 那神马是单点修改和区间查询?我们来看一道题。 洛谷P3374(模板): 在本题中,单点修改就是将某一个数加上…...
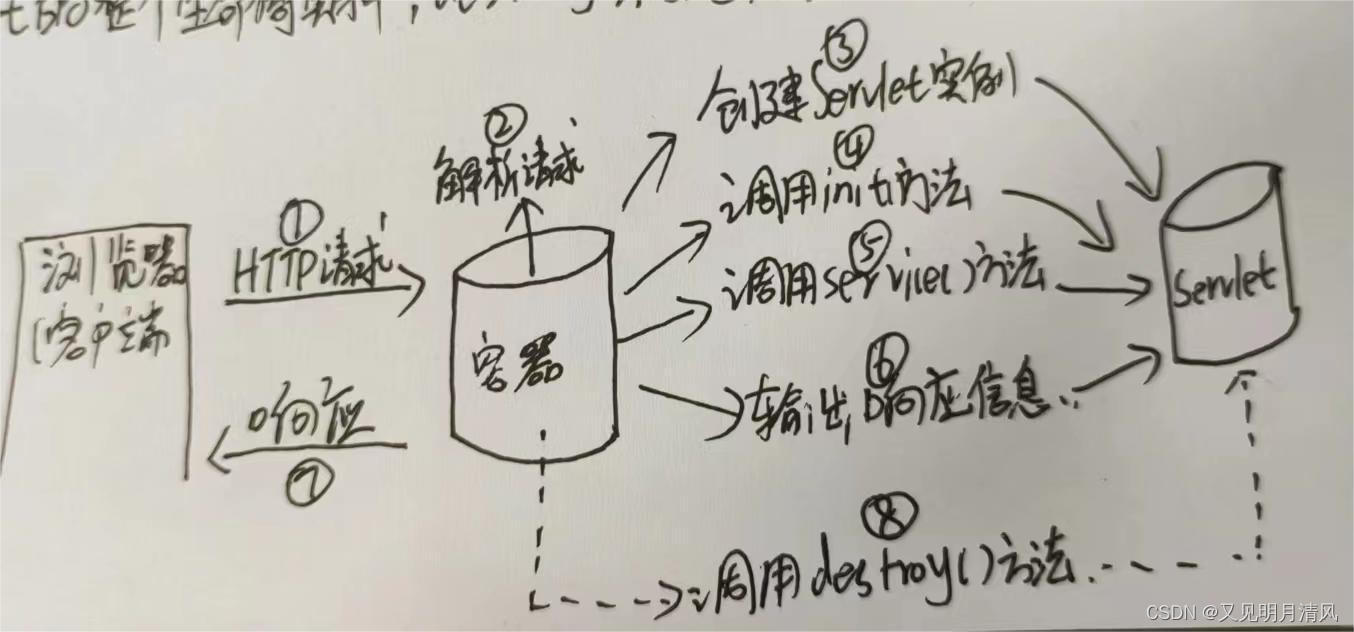
Servlet生命周期
第一阶段: init()初始化阶段 当客户端想Servlet容器(例如Tomcat)发出HTTP请求要求访问Servlet时,Servlet容器首先会解析请求,检查内存中是否已经有了该Servlet对象,如果有ÿ…...
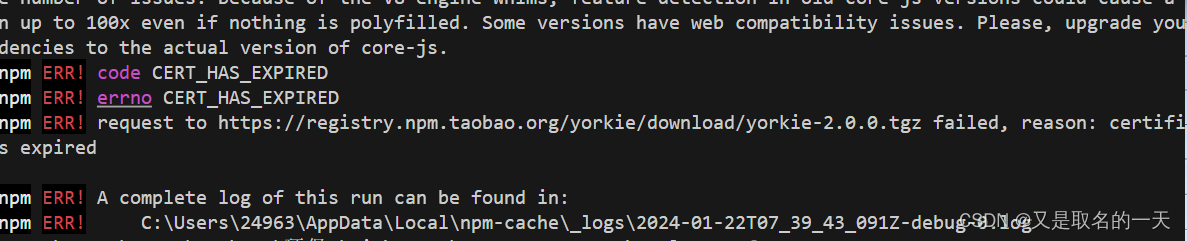
npm i 报一堆版本问题
1,先npm cache clean --force 再下载 插件后缀加上 --legacy-peer-deps 2, npm ERR! code CERT_HAS_EXPIRED npm ERR! errno CERT_HAS_EXPIRED npm ERR! request to https://registry.npm.taobao.org/yorkie/download/yorkie-2.0.0.tgz failed, reason…...

Linux设备管理模型-01:基础数据结构
文章目录 1. 设备管理模型2. 基本数据结构2.1 kobject2.2 kset 1. 设备管理模型 设备模型是内核提供的一个编写驱动的架构。 设备管理是设备-总线-驱动结构。 linux中的设备是由树状模型组织的,从sysfs中可以查看树状结构。 他本身实现了: 电源管理热…...
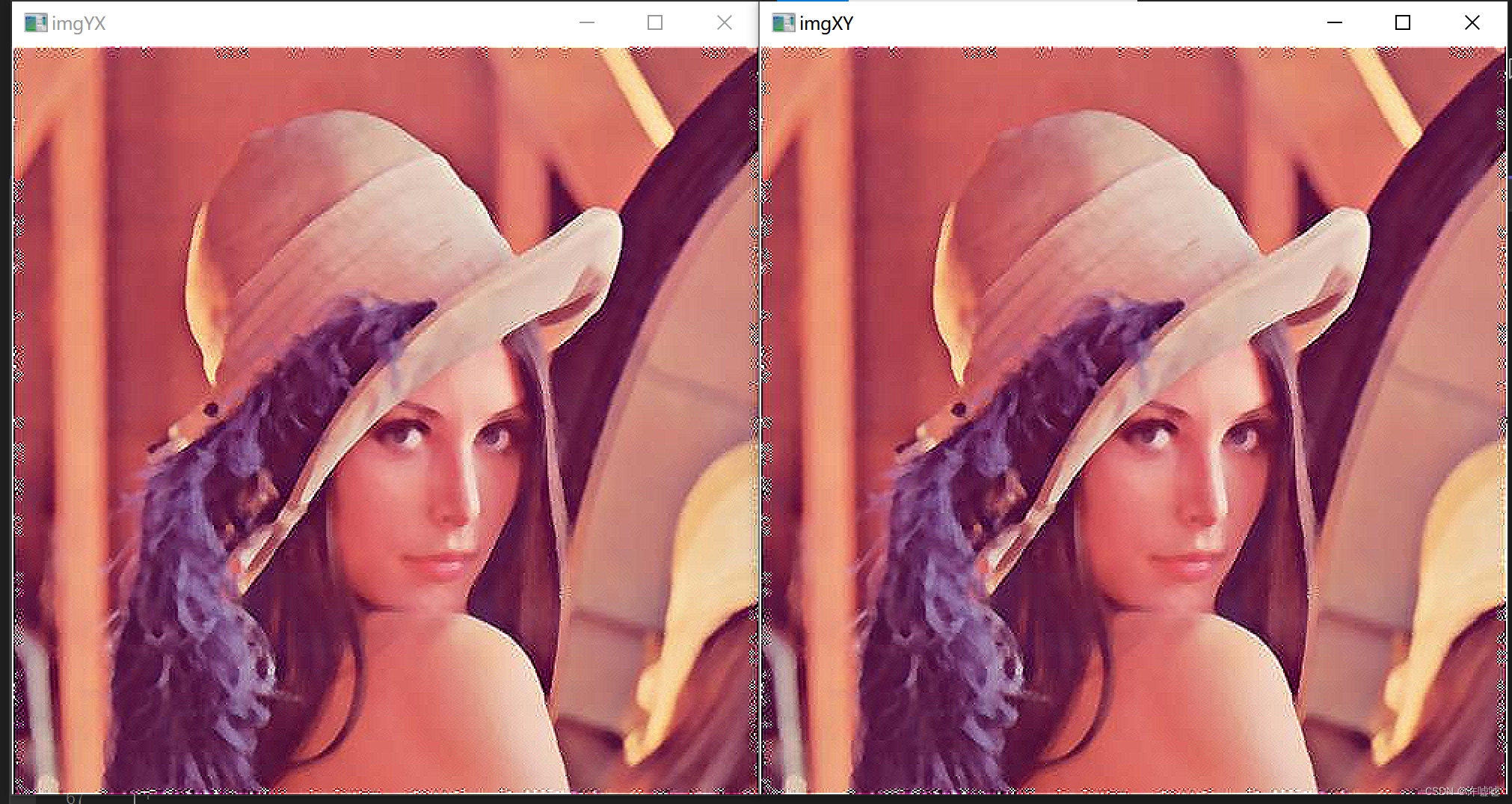
opencv#32 可分离滤波
滤波的可分离性 就是将一个线性滤波变成多个线性滤波,这里面具体所指的是变成x方向的线性滤波和y方向的线性滤波。无论先做x方向的滤波还是y方向滤波,两者的叠加结果是一致的,这个性质取决于滤波操作是并行的,也就是每一个图像在滤…...

android 导航app 稳定性问题总结
一 重写全局异常处理: 1 是过滤掉一些已知的无法处理的 问题,比如TimeoutException 这种无法根除只能缓解的问题可以直接catch掉 2 是 一些无法继续的问题可以直接杀死重启,一些影响不是很大的,可以局部还原 比如: p…...
第11次修改了可删除可持久保存的前端html备忘录:将样式分离,可以自由秒添加秒删除样式
第11次修改了可删除可持久保存的前端html备忘录:将样式分离,可以自由秒添加秒删除样式 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport" content"…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
