Numpy专栏目录(长期更新)
文章目录
- 数组基础
- 文件与字符串
- 多项式
- 分布
Numpy绝对可以说是支撑Python地位的最重要的包了,几乎所有能叫出名的Python计算库,都不可避免地调用了Numpy,Numpy官网也列出了一些,大致如下图这样,堪称科学计算领域的瑞士军刀的刀把了。

数组基础
- 高性能计算数组array
- 数组生成:等差数组💎坐标网格💎特殊数组💎数组形状调整
- 常用函数:数学函数💎排序函数💎统计函数💎逻辑和位处理函数
- 数值差分💎数值积分💎傅里叶变换
- 线性代数
文件与字符串
字符串数组
文本读写
用fromfile和tofile读写文件
npy和npz
多项式
Numpy.polynomial中封装了六种多项式类,除了常规的多项式a0+a1x+⋯+anxna_0+a_1x+\cdots+a_nx^na0+a1x+⋯+anxn之外,还有五种在数学、物理中常用的正交多项式,例如Hermite多项式在量子力学中是谐振子的本征态;Legendre多项式可表示点电荷在空间中的激发电势;切比雪夫多项式可用于缓解龙格现象;拉盖尔多项式则是氢原子基函数的径向部分,下表是这些多项式在numpy中封装的类以及各阶表达式。
| 类和链接 | 中文名称 | 第n阶表达式 |
|---|---|---|
| Polynomial | 多项式 | xnx^nxn |
| Chebyshev | 第一类切比雪夫多项式 | cos(narccosx)\cos(n\arccos x)cos(narccosx) |
| Legendre | 勒让德多项式 | 12nn!dndxn(x2−1)n\frac{1}{2^nn!}\frac{\text d^n}{\text dx^n}(x^2-1)^n2nn!1dxndn(x2−1)n |
| Laguerre | 拉盖尔多项式 | exn!dndxn(e−xxn)\frac{e^x}{n!}\frac{\text d^n}{\text dx^n}(e^{-x}x^n)n!exdxndn(e−xxn) |
| Hermite | 埃尔米特多项式(物理) | (−1)nex2dndxne−x2(-1)^ne^{x^2}\frac{\text d^n}{\text dx^n}e^{-x^2}(−1)nex2dxndne−x2 |
| HermiteE | 埃尔米特多项式(统计) | (−1)nex2/2dndxne−x2/2(-1)^ne^{x^2/2}\frac{\text d^n}{\text dx^n}e^{-x^2/2}(−1)nex2/2dxndne−x2/2 |
这六个类对函数的封装十分相似,所以后面又写了个总结:多项式总结
分布
np.random中提供了一系列的分布函数,用以生成符合某种分布的随机数,本专栏从原理到代码,对这些分布进行逐一讲解,兼顾对不同分布之间联系的分析。
| 函数 | 概率密度函数(PDF) | 备注和链接 |
|---|---|---|
binomial | p(N)=(nN)pN(1−p)n−Np(N) = \binom{n}{N}p^N(1-p)^{n-N}p(N)=(Nn)pN(1−p)n−N | 二项分布 |
multinomial | 多项分布 | |
geometric | f(n)=(1−p)n−1pf(n)=(1-p)^{n-1}pf(n)=(1−p)n−1p | 几何分布 |
negative_binomial | p(N)=Γ(N+n)N!Γ(n)pn(1−p)Np(N)=\frac{\Gamma(N+n)}{N!\Gamma(n)}p^n(1-p)^Np(N)=N!Γ(n)Γ(N+n)pn(1−p)N | 负二项分布 |
poisson | f(k)=λke−λk!f(k)=\frac{\lambda^ke^{-\lambda}}{k!}f(k)=k!λke−λ | 泊松分布 |
logseries | p(k)=−pkkln(1−p)p(k)=\frac{-p^k}{k\ln(1-p)}p(k)=kln(1−p)−pk | 对数级数分布 |
gamma | p(x)=xk−1e−x/θθkΓ(k)p(x)=x^{k-1}\frac{e^{-x/\theta}}{\theta^k\Gamma(k)}p(x)=xk−1θkΓ(k)e−x/θ | 伽马分布 |
beta | Γ(a+b)Γ(a)Γ(b)xa−1(1−x)b−1\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}x^{a-1}(1-x)^{b-1}Γ(a)Γ(b)Γ(a+b)xa−1(1−x)b−1 | 贝塔分布 |
dirichlet | p(x)=∏i=1kxiαi−1p(x)=\prod_{i=1}^kx_i^{\alpha_i-1}p(x)=∏i=1kxiαi−1 | 狄利克雷分布 |
logistic | p(x)=(x−μ)/ss(1+exp[−(x−μ)/s])2p(x)=\frac{(x-\mu)/s}{s(1+\exp[-(x-\mu)/s])^2}p(x)=s(1+exp[−(x−μ)/s])2(x−μ)/s | Logistic分布 |
triangular | 分段函数 | 三角形分布 |
uniform | p(x)=1b−ap(x)=\frac{1}{b-a}p(x)=b−a1 | 均匀分布 |
vonmises | p(x)=exp[κ(x−μ)]2πI0(κ)p(x)=\frac{\exp[{\kappa(x-\mu)}]}{2\pi I_0(\kappa)}p(x)=2πI0(κ)exp[κ(x−μ)] | von Mises分布 |
zipf | p(k)=k−aζ(a)p(k)=\frac{k^{-a}}{\zeta(a)}p(k)=ζ(a)k−a | 齐普夫分布 |
pareto | p(x)=maxap(x)=\frac{m^a}{x^{a}}p(x)=xama | 帕累托分布 |
power | p(x)=axa−1p(x)=ax^{a-1}p(x)=axa−1 | 幂分布 |
gumbel | exp[−z−e−z],z=x−μλ\exp[{-z-e^{-z}}], z=\frac{x-\mu}{\lambda}exp[−z−e−z],z=λx−μ | 耿贝尔分布 |
chisquare | (1/2)k/2Γ(k/2)xk/2−1e−x/2\frac{(1/2)^{k/2}}{\Gamma(k/2)}x^{k/2-1}e^{-x/2}Γ(k/2)(1/2)k/2xk/2−1e−x/2 | 卡方分布 |
weibull | p(x)=aλ(xλ)a−1e−(x/λ)ap(x)=\frac{a}{\lambda}(\frac{x}{\lambda})^{a-1}e^{-(x/\lambda)^a}p(x)=λa(λx)a−1e−(x/λ)a | 威布尔分布 |
rayleigh | p(x)=xλ2exp[−x22λ2]p(x)=\frac{x}{\lambda^2}\exp[\frac{-x^2}{2\lambda^2}]p(x)=λ2xexp[2λ2−x2] | 瑞利分布 |
exponential | f(x)=1λexp−xλf(x)=\frac{1}{\lambda}\exp{-\frac{x}{\lambda}}f(x)=λ1exp−λx | 指数分布 |
laplace | f(x)=12λexp[−∣x−μ∣λ]f(x)=\frac{1}{2\lambda}\exp[-\frac{\vert x-\mu\vert}{\lambda}]f(x)=2λ1exp[−λ∣x−μ∣] | 拉普拉斯分布 |
相关文章:

Numpy专栏目录(长期更新)
文章目录数组基础文件与字符串多项式分布Numpy绝对可以说是支撑Python地位的最重要的包了,几乎所有能叫出名的Python计算库,都不可避免地调用了Numpy,Numpy官网也列出了一些,大致如下图这样,堪称科学计算领域的瑞士军刀…...
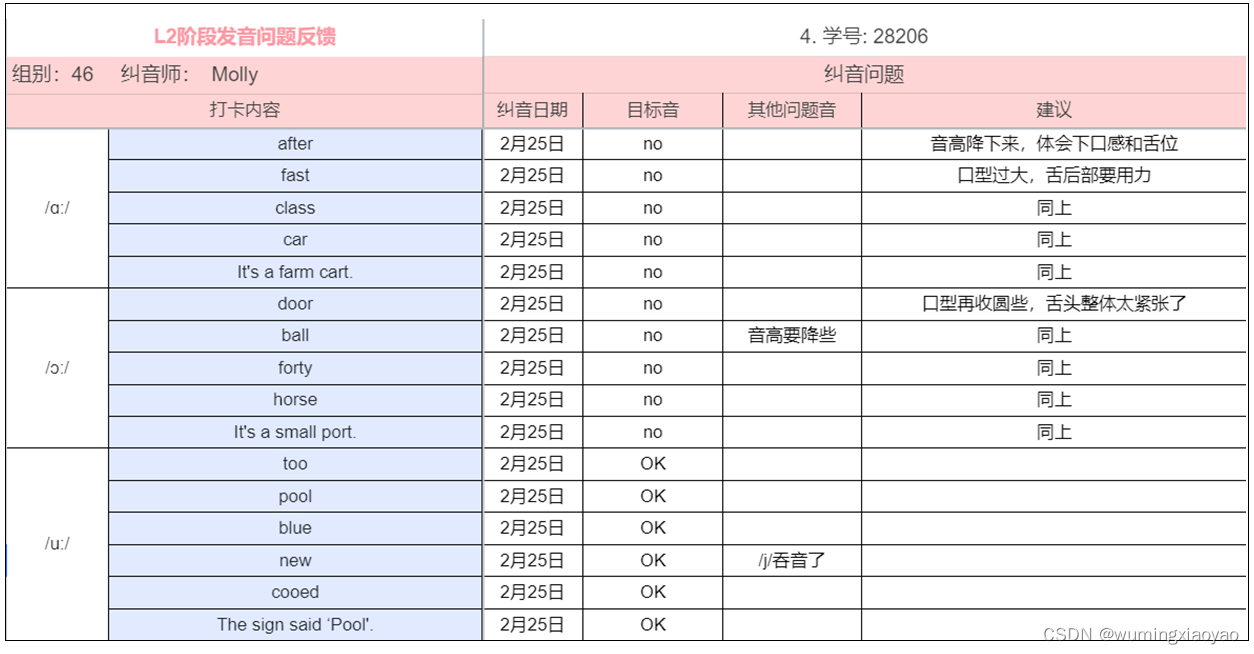
English Learning - L2 第1次小组纠音 [ɑː] [ɔː] [uː] 2023.2.25 周六
English Learning - L2 第1次小组纠音 [ɑː] [ɔː] [uː] 2023.2.25 周六共性问题分析大后元音 [ɑː]大后元音 [ɔː]后元音 [uː]我的发音问题后元音 [uː]大后元音 [ɑː] 和 [ɔː]纠音过程第一次第二次第三次共性问题分析 大后元音 [ɑː] 嘴唇过于松散,没…...
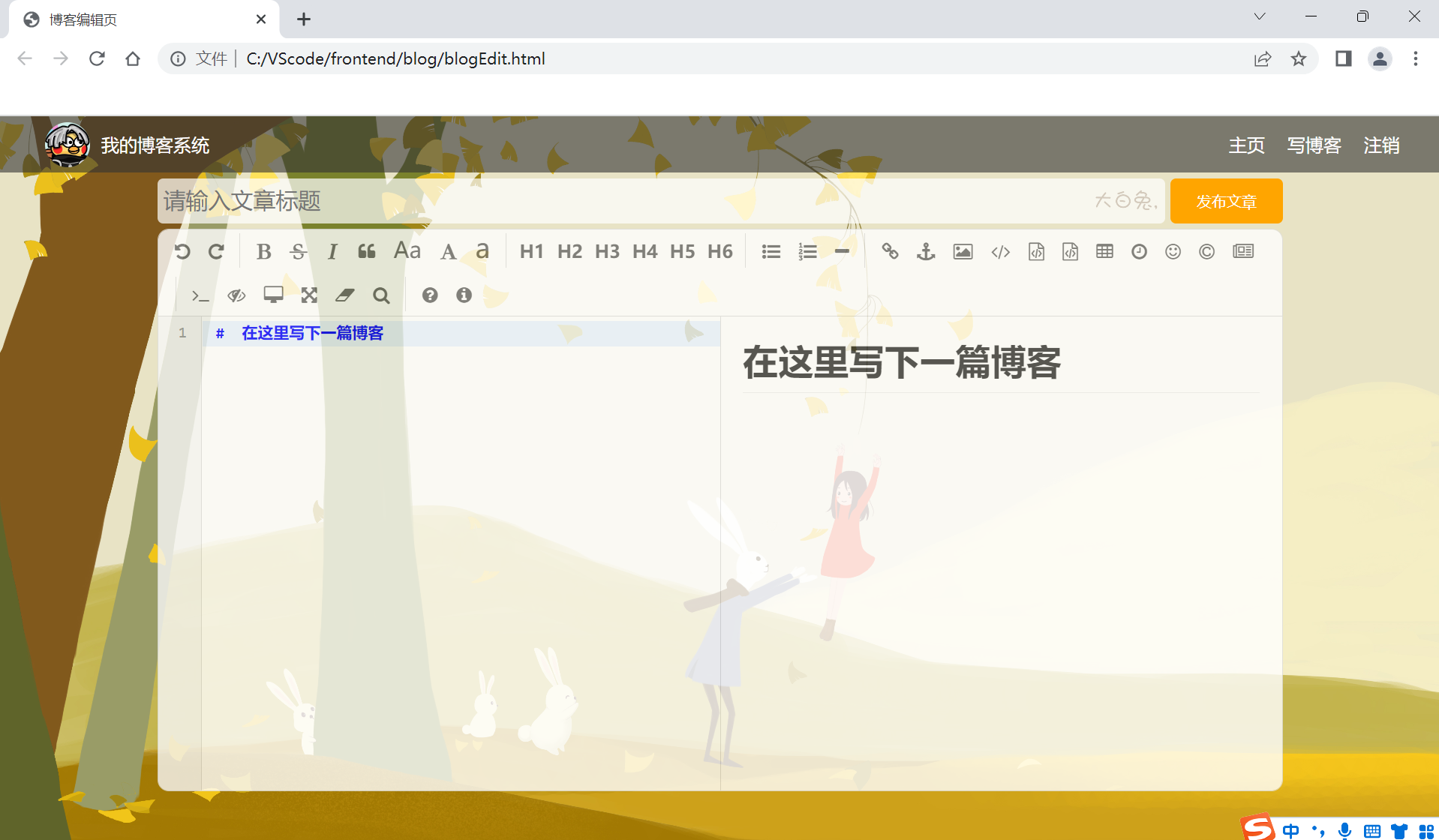
博客系统程序(页面设计)
咱们学习javaEE的目的就是完成一个网站.在当前学习的基础上,已经可以完成我们的博客系统的页面的设计了!!!首先我们要进行统筹规划:首先我们的博客页面将会有4个页面:1.博客列表页2.博客详情页显示一个博客的具体内容:3.登录页就是用户输入用户名和页面的地方4.博客编辑页发布新…...

【死锁的排查工具有哪些?】
死锁是指两个或多个进程(线程)相互等待对方持有的资源,导致无法继续执行的情况。在并发编程中,死锁是一个常见的问题,需要使用专门的工具来进行排查和解决。 以下是常用的死锁排查工具: jstack:…...

JUC包:CyclicBarrier源码+实例讲解
1 缘起 上篇文章讲到了CountDownLatch:https://blog.csdn.net/Xin_101/article/details/129116170 作为同系的佼佼者,不得不提CyclicBarrier, 设计理念相似,都是多线程等待,但是,应用的技术以及功能不同&a…...

Trace、Metrics、Logging 选型
背景分布式追踪的起源自从微服务的兴起开始,整个系统架构开始变得极为庞大和复杂,但是服务之间的调用关系,调用消耗时间等等信息却依然是半黑盒的状态。为了能够将调用的链路进行串联,将系统的各种指标数据展示出来以使得系统的链…...

Java验证码
文章目录一、验证码概述二、Java原生验证码1、随机数字验证码2、随机数字和字母验证码3、运算验证码三、引入三方验证码一、验证码概述 验证码(CAPTCHA)是“Completely Automated Public Turing test to tell Computers and Humans Apart”(全…...
)
5天带你读完《Effective Java》(四)
《Effective Java》是Java开发领域无可争议的经典之作,连Java之父James Gosling都说: “如果说我需要一本Java编程的书,那就是它了”。它为Java程序员提供了90个富有价值的编程准则,适合对Java开发有一定经验想要继续深入的程序员…...

探索密码学的未来:SM1、SM2、SM3、SM4、同态加密、密态计算、隐私计算和安全多方计算
密码算法在现代通信与信息安全中发挥着至关重要的作用,SM1、SM2、SM3、SM4、同态加密、密态计算、隐私计算和安全多方计算等密码算法被广泛应用于各种信息安全领域。本篇博客将会为大家介绍这些密码算法,以及它们在信息安全中的作用和应用。 一、SM1、SM…...
【教程】去水印开源工具Lama Cleaner在Windows的安装和使用
一、Lama Cleaner是什么? Lama Cleaner是一款开源且免费的人工学习图片去水印程序(个人主要学习用途),没有图片分辨率限制(个人使用暂未发现),并且保存的图片质量很高(个人觉得跟原…...

驾考笔记_2023
科目一1> 扣分制度1.1> 超速1.2> 超载1.3> 车牌1.4> 速记口诀2> 满分学习2.1> 消分学习2.2> 满分重考;3> 罚款 / 判刑3.1> 考证3.2> 审验教育3.3> 酒驾3.4> 200¥3.5> 500¥3.6> 2000¥…...
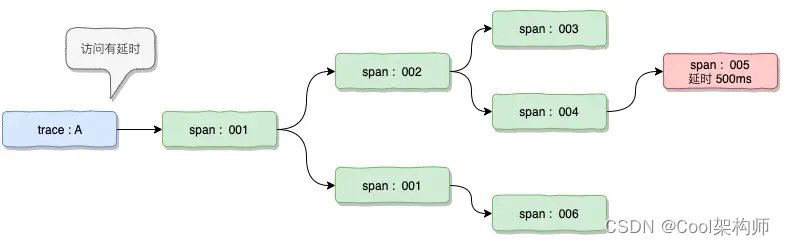
【架构师】跟我一起学架构——调用链
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小留言…...
[神经网络]Swin Transformer网络
一、概述 Swin Transformer是一个用了移动窗口的层级式Vision Transformer。 在图像领域,Transformer需要解决如下两个问题: ①尺度问题:同一语义的物体在图像中有不一样的尺度。(大小不同) ②Resolution过大:若以像素点作为单位&…...
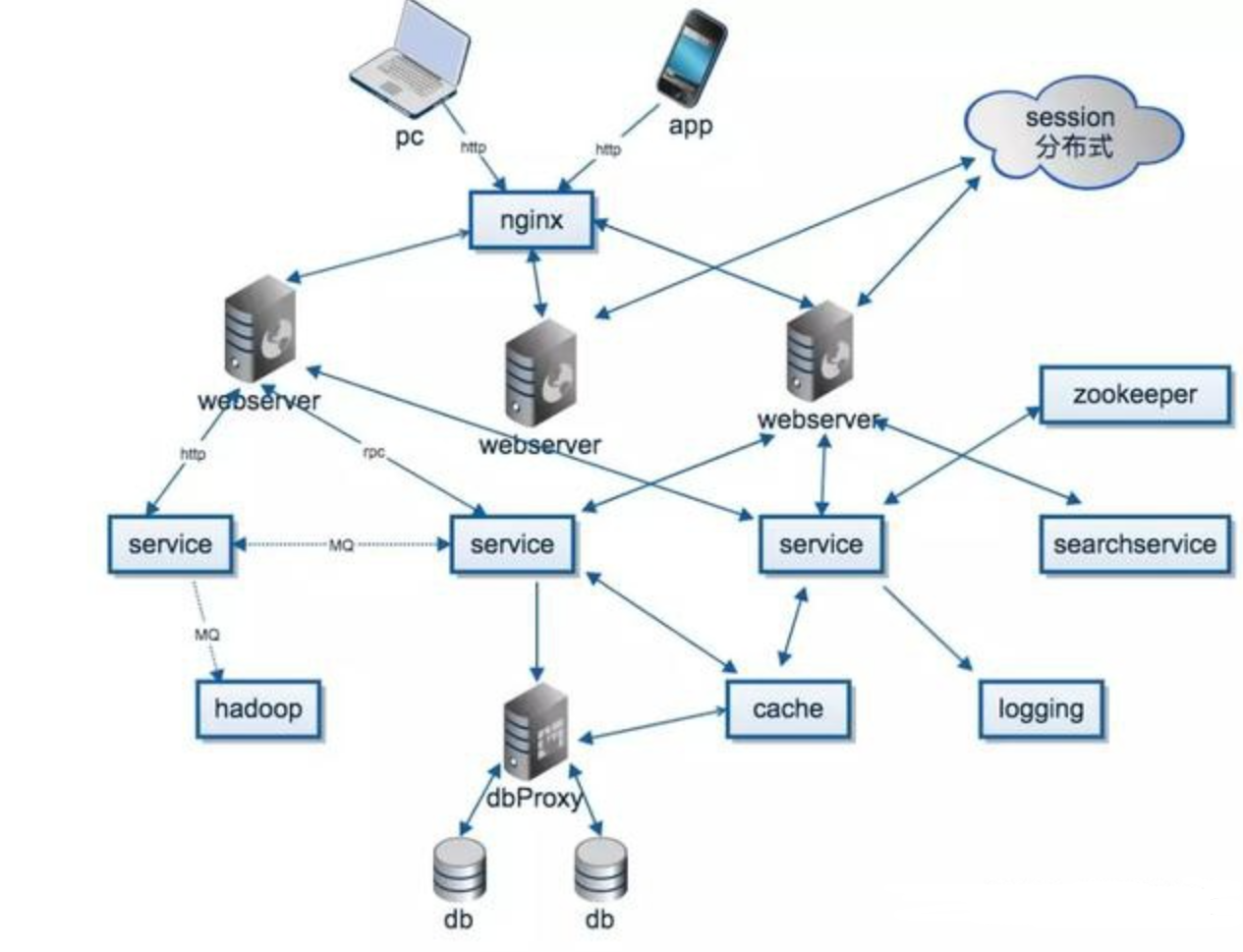
【分布式】什么是分布式,分布式和集群的区别又是什么?答案在正文。
文章目录1. 什么是分布式 ?2. 分布式与集群的区别 ?3.用一个请求串起来4.一个简化的架构图5.分布式环境的特点6.分布式环境下面临的问题7.总结1. 什么是分布式 ? 分布式系统一定是由多个节点组成的系统。 其中,节点指的是计算机服务器,而且这些节点一…...

MyBatis框架的入门案例
MyBatis框架的入门案例 资源地址:https://download.csdn.net/download/weixin_41957626/87531373 1.MyBatis的配置 环境:基于maven的结构 1.1目录结构 1.2依赖包 <dependencies><!--mybatis--><dependency><groupId>org.mybatis…...
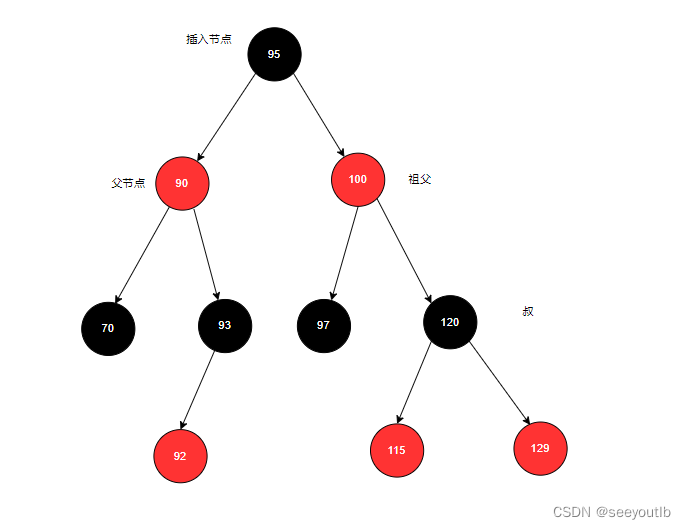
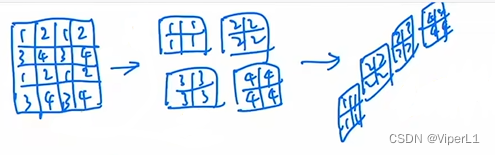
红黑树-随记
文章目录1.为什么hashmap用红黑树不用二叉树和平衡二叉树1.1 二叉树(Binary Search Tree)1.2 红黑树(Red Black Tree)1.3 平衡二叉树(Balence Binary Tree)也称AVT2.为什么mysql用b数,不用B数或…...

Python异常处理更新,正常和不正常的都在这里
嗨害大家好鸭!我是小熊猫~ 异常处理篇嗨害大家好鸭!我是小熊猫~Python标准异常💨什么是异常?不正常异常处理💨使用except而不带任何异常类型使用except而带多种异常类型try-finally 语句异常的参数触发异常用户自定义异…...
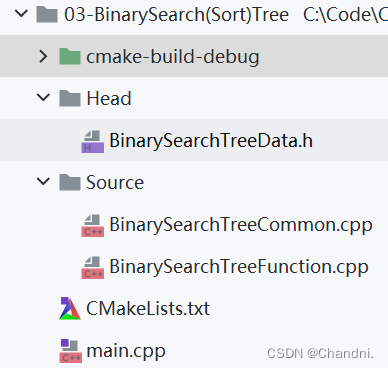
[数据结构]:10-二叉排序树(无头结点)(C语言实现)
目录 前言 已完成内容 二叉排序树实现 01-开发环境 02-文件布局 03-代码 01-主函数 02-头文件 03-BinarySearchTreeCommon.cpp 04-BinarySearchTreeFunction.cpp 结语 前言 此专栏包含408考研数据结构全部内容,除其中使用到C引用外,全为C语言…...

openstack浅析
** OpenStack是一个由多个组件组成的开源云计算平台,每个组件都有不同的功能和用途。 ** 组件构成 以下是OpenStack中一些常见的组件及其功能: Nova:用于管理虚拟机的组件,提供了虚拟机的创建、销毁、管理等功能。 Neutron&am…...

华为OD机试Golang解题 - 特异性双端队列 | 含思路
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
