探索密码学的未来:SM1、SM2、SM3、SM4、同态加密、密态计算、隐私计算和安全多方计算
密码算法在现代通信与信息安全中发挥着至关重要的作用,SM1、SM2、SM3、SM4、同态加密、密态计算、隐私计算和安全多方计算等密码算法被广泛应用于各种信息安全领域。本篇博客将会为大家介绍这些密码算法,以及它们在信息安全中的作用和应用。
一、SM1、SM2、SM3、SM4
SM1、SM2、SM3、SM4是中国国家密码管理局发布的四个密码算法标准。SM1是一种对称密码算法,SM2是一种非对称密码算法,SM3是一种哈希函数,SM4是一种分组对称密码算法。
SM1算法采用分组加密模式,将明文分成多个固定长度的数据块,每个数据块分别进行加密操作。SM1的加密过程中包括了置换、代换、线性变换等步骤,从而保证了加密的强度和安全性。
SM2算法是一种基于椭圆曲线密码体制的公钥密码算法,可以用于数字签名、密钥协商、加密和解密等操作。SM2的安全性基于离散对数问题的难度,通过椭圆曲线的运算实现加密和解密操作。
SM3算法是一种哈希函数,用于对任意长度的消息进行摘要操作,可以生成一个固定长度的消息摘要。SM3算法采用了置换、代换、移位、加法等操作,可以保证摘要的强度和唯一性。
SM4算法是一种分组对称密码算法,采用Feistel结构,将明文分成多个数据块,每个数据块分别进行加密操作。SM4算法采用了S盒、置换、线性变换等操作,从而保证了加密的强度和安全性。
二、同态加密
同态加密是一种特殊的加密技术,它可以在不暴露明文的情况下进行加法和乘法运算。同态加密可以用于云计算、安全多方计算等场景中,实现数据的保护和隐私计算。
同态加密可以分为完全同态加密和部分同态加密。完全同态加密可以进行任意次的加法和乘法运算,而部分同态加密只能进行有限次的加法或乘法运算。
同态加密的实现需要满足两个基本要求:保证加密后的密文能够进行运算,且运算后得到的结果是正确的。同态加密技术的实现需要借助数学理论,
具体来说,同态加密算法需要满足以下两个条件:
- 加密后的密文可以进行加法和乘法运算。
在传统的加密算法中,加密后的密文是无法进行运算的,只能通过解密后再进行计算。但是,在同态加密中,密文是可以进行加法和乘法运算的,这是实现同态计算的基础。
- 运算后得到的结果是正确的。
在同态加密中,由于密文已经被加密,直接进行加法和乘法运算得到的结果不一定是正确的,需要通过一系列复杂的算法来确保运算结果正确。
实现同态加密技术需要借助多项式环、理想、剩余系等数学理论,如Paillier同态加密算法、Gentry同态加密算法等。
同态加密技术的应用非常广泛,如在云计算中,可以将数据加密后上传到云端,实现数据的保护和隐私计算;在安全多方计算中,可以在不暴露数据的情况下进行数据合并和分析。
三、密态计算
密态计算是一种保护隐私数据的计算技术,它可以在不暴露原始数据的情况下进行数据处理和分析。密态计算可以保证数据的隐私性、安全性和完整性,是一种非常重要的隐私保护技术。
密态计算可以分为两种类型:基于加密的密态计算和基于扰动的密态计算。基于加密的密态计算是指对原始数据进行加密后再进行计算,而基于扰动的密态计算是指对原始数据进行一定的扰动后再进行计算。
密态计算的实现需要满足以下三个基本要求:
-
隐私保护。密态计算需要保护原始数据的隐私,确保数据不被泄露。
-
安全性。密态计算需要确保计算的过程是安全的,防止被攻击者利用漏洞进行攻击。
-
计算正确性。密态计算需要确保计算结果是正确的,保证数据的完整性。
密态计算可以应用于各种领域,如金融、医疗、社交网络等,实现隐私保护和数据处理的需求。
四、隐私计算
隐私计算是一种保护数据隐私的计算技术,它可以在不暴露原始数据的情况下进行数据处理和分析。隐私计算可以保证数据的隐私性、安全性和完整性,是一种非常重要的隐私保护
技术。
隐私计算可以分为基于加密的隐私计算和基于差分隐私的隐私计算。基于加密的隐私计算是指对原始数据进行加密后再进行计算,而基于差分隐私的隐私计算是指对原始数据进行一定的扰动后再进行计算。相比之下,基于差分隐私的隐私计算更加适用于大规模数据的隐私保护。
隐私计算的实现需要满足以下三个基本要求:
-
隐私保护。隐私计算需要保护原始数据的隐私,确保数据不被泄露。
-
安全性。隐私计算需要确保计算的过程是安全的,防止被攻击者利用漏洞进行攻击。
- 计算正确性。隐私计算需要确保计算结果是正确的,保证数据的完整性。
隐私计算可以应用于各种领域,如金融、医疗、社交网络等,实现隐私保护和数据处理的需求。例如,在金融领域,可以通过隐私计算对客户数据进行处理和分析,以便银行机构更好地了解客户需求和行为,提供更好的服务和产品。在医疗领域,可以通过隐私计算对患者数据进行处理和分析,以便医疗机构更好地了解疾病情况和治疗效果,提供更好的医疗服务。在社交网络领域,可以通过隐私计算对用户数据进行处理和分析,以便社交平台更好地了解用户需求和行为,提供更好的用户体验和服务。
五、安全多方计算
安全多方计算是一种在多个参与方之间进行计算的技术,可以在保护数据隐私的前提下,实现数据的共享和处理。安全多方计算可以应用于各种领域,如金融、医疗、社交网络等。
安全多方计算可以分为两种类型:基于密码学的安全多方计算和基于秘密共享的安全多方计算。基于密码学的安全多方计算是指在计算过程中,参与方对数据进行加密和解密,以保护数据隐私;而基于秘密共享的安全多方计算是指在计算过程中,参与方将数据进行分割,各自保存一部分数据,并在计算过程中进行数据合并和分析。
安全多方计算的实现需要满足以下三个基本要求:
隐私保护 安全多方计算需要确保数据隐私得到充分保护,不会被恶意方窃取或泄露。
安全性 安全多方计算需要确保计算的过程是安全的,防止被攻击者利用漏洞进行攻击。
计算正确性 安全多方计算需要确保计算结果是正确的,保证数据的完整性和可靠性。
安全多方计算可以应用于多种领域,例如金融、医疗、社交网络等。在金融领域,安全多方计算可以被用来实现多方合作的金融风险管理、信用评估、客户身份验证等业务。在医疗领域,安全多方计算可以被用来实现多方协作的医学研究、疾病诊断、健康管理等业务。在社交网络领域,安全多方计算可以被用来实现多方协作的社交分析、广告推送、用户画像等业务。
总之,安全多方计算是一种非常重要的计算技术,可以在保护数据隐私的同时,实现数据的共享和处理,为各种应用场景提供强有力的支持。
相关文章:

探索密码学的未来:SM1、SM2、SM3、SM4、同态加密、密态计算、隐私计算和安全多方计算
密码算法在现代通信与信息安全中发挥着至关重要的作用,SM1、SM2、SM3、SM4、同态加密、密态计算、隐私计算和安全多方计算等密码算法被广泛应用于各种信息安全领域。本篇博客将会为大家介绍这些密码算法,以及它们在信息安全中的作用和应用。 一、SM1、SM…...
【教程】去水印开源工具Lama Cleaner在Windows的安装和使用
一、Lama Cleaner是什么? Lama Cleaner是一款开源且免费的人工学习图片去水印程序(个人主要学习用途),没有图片分辨率限制(个人使用暂未发现),并且保存的图片质量很高(个人觉得跟原…...

驾考笔记_2023
科目一1> 扣分制度1.1> 超速1.2> 超载1.3> 车牌1.4> 速记口诀2> 满分学习2.1> 消分学习2.2> 满分重考;3> 罚款 / 判刑3.1> 考证3.2> 审验教育3.3> 酒驾3.4> 200¥3.5> 500¥3.6> 2000¥…...
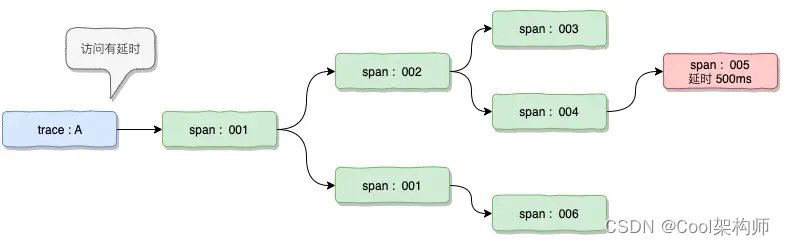
【架构师】跟我一起学架构——调用链
博客昵称:架构师Cool 最喜欢的座右铭:一以贯之的努力,不得懈怠的人生。 作者简介:一名Coder,软件设计师/鸿蒙高级工程师认证,在备战高级架构师/系统分析师,欢迎关注小弟! 博主小留言…...
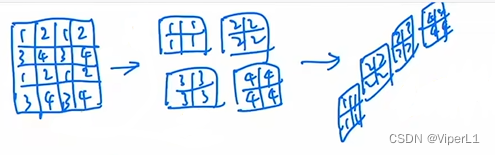
[神经网络]Swin Transformer网络
一、概述 Swin Transformer是一个用了移动窗口的层级式Vision Transformer。 在图像领域,Transformer需要解决如下两个问题: ①尺度问题:同一语义的物体在图像中有不一样的尺度。(大小不同) ②Resolution过大:若以像素点作为单位&…...
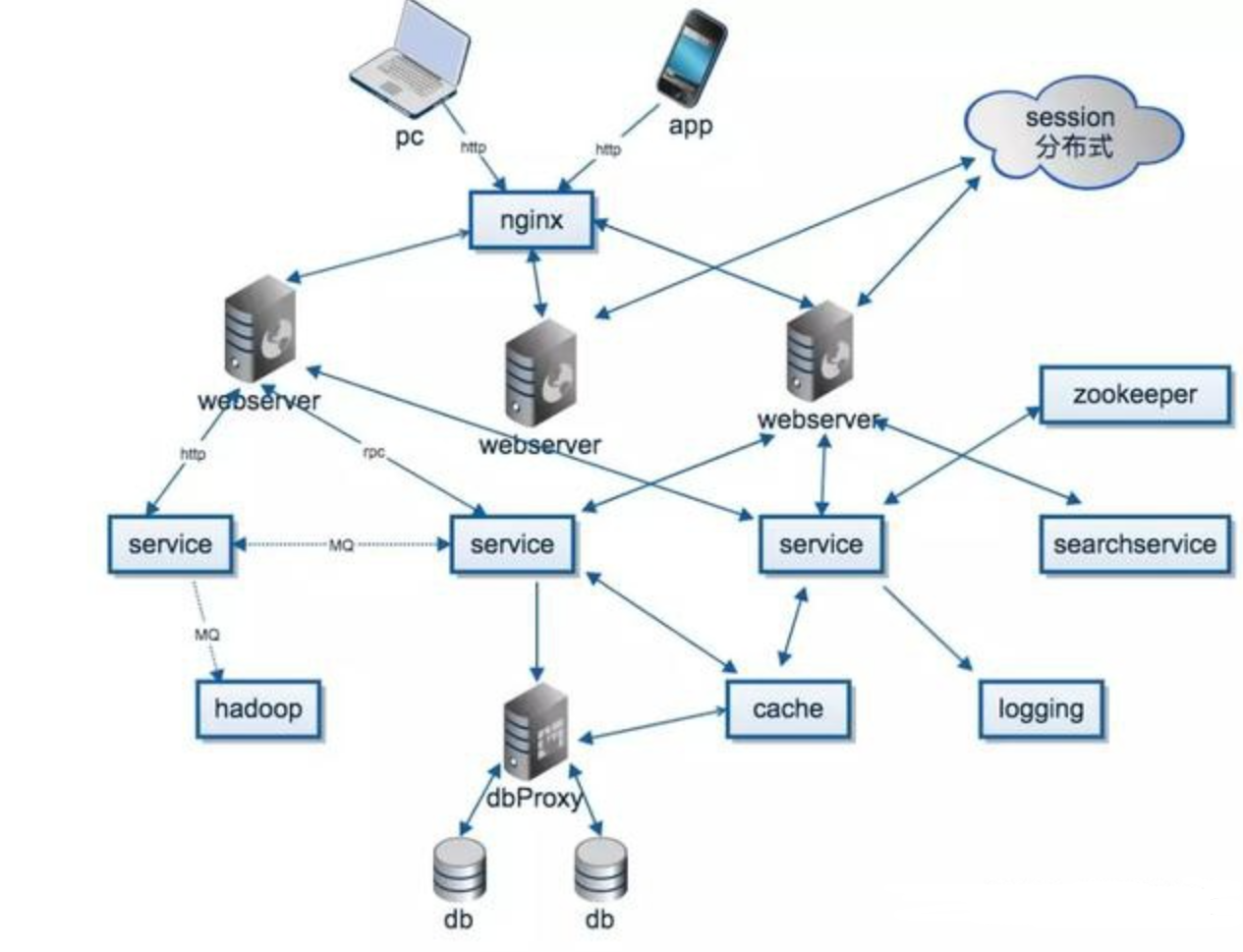
【分布式】什么是分布式,分布式和集群的区别又是什么?答案在正文。
文章目录1. 什么是分布式 ?2. 分布式与集群的区别 ?3.用一个请求串起来4.一个简化的架构图5.分布式环境的特点6.分布式环境下面临的问题7.总结1. 什么是分布式 ? 分布式系统一定是由多个节点组成的系统。 其中,节点指的是计算机服务器,而且这些节点一…...

MyBatis框架的入门案例
MyBatis框架的入门案例 资源地址:https://download.csdn.net/download/weixin_41957626/87531373 1.MyBatis的配置 环境:基于maven的结构 1.1目录结构 1.2依赖包 <dependencies><!--mybatis--><dependency><groupId>org.mybatis…...
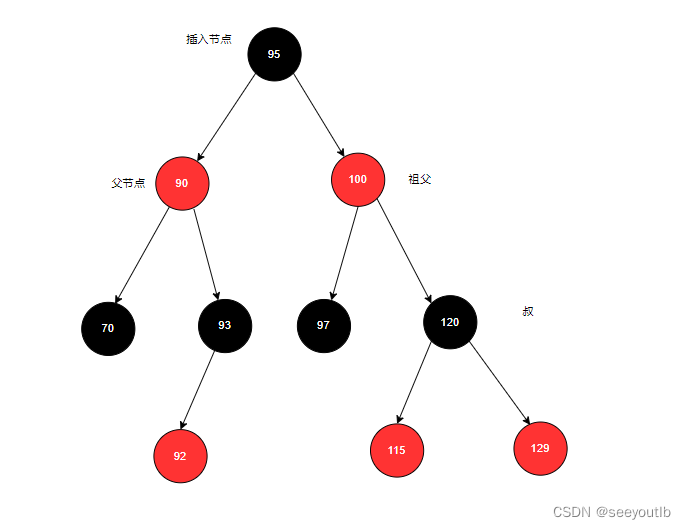
红黑树-随记
文章目录1.为什么hashmap用红黑树不用二叉树和平衡二叉树1.1 二叉树(Binary Search Tree)1.2 红黑树(Red Black Tree)1.3 平衡二叉树(Balence Binary Tree)也称AVT2.为什么mysql用b数,不用B数或…...

Python异常处理更新,正常和不正常的都在这里
嗨害大家好鸭!我是小熊猫~ 异常处理篇嗨害大家好鸭!我是小熊猫~Python标准异常💨什么是异常?不正常异常处理💨使用except而不带任何异常类型使用except而带多种异常类型try-finally 语句异常的参数触发异常用户自定义异…...
[数据结构]:10-二叉排序树(无头结点)(C语言实现)
目录 前言 已完成内容 二叉排序树实现 01-开发环境 02-文件布局 03-代码 01-主函数 02-头文件 03-BinarySearchTreeCommon.cpp 04-BinarySearchTreeFunction.cpp 结语 前言 此专栏包含408考研数据结构全部内容,除其中使用到C引用外,全为C语言…...

openstack浅析
** OpenStack是一个由多个组件组成的开源云计算平台,每个组件都有不同的功能和用途。 ** 组件构成 以下是OpenStack中一些常见的组件及其功能: Nova:用于管理虚拟机的组件,提供了虚拟机的创建、销毁、管理等功能。 Neutron&am…...

华为OD机试Golang解题 - 特异性双端队列 | 含思路
华为Od必看系列 华为OD机试 全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典文章目录 华为Od必看系列使用说明本期题目…...
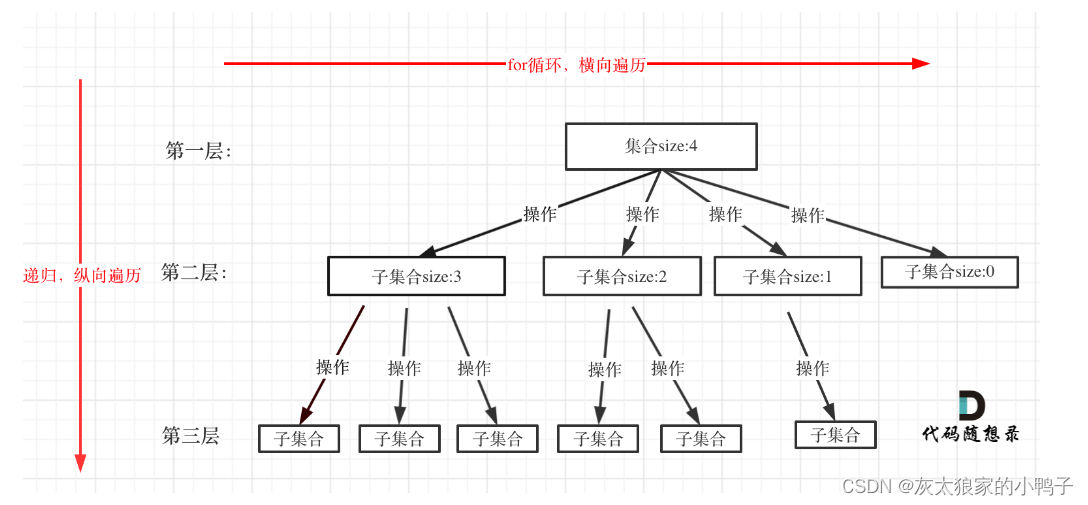
代码随想录中:回溯算法的基础
回溯算法是一种暴力的搜索方式;回溯法一般与递归同时存在。 回溯法,一般可以解决如下几种问题: 组合问题:N个数里面按一定规则找出k个数的集合切割问题:一个字符串按一定规则有几种切割方式子集问题:一个…...
Jetpack系列之LiveData)
Android kotlin 系列讲解(进阶篇)Jetpack系列之LiveData
<<返回总目录 文章目录 一、LiveData是什么二、LiveData测试一、LiveData是什么 LiveData是Jetpack提供的一种响应式编程组件,它可以包括任何类型的数据,并在数据发生变化的时候通知给观察者。LiveData特别适合与ViewModel结合在一起使用,虽然它也可以单独在别的地方…...

如何判断有向无环图:构造有向无环图
拓扑序列:可以用来判断一个有向图是否有环! 拓扑排序可以判断有向图是否存在环。我们可以对任意有向图执行上述过程,在完成后检查A序列的长度。 若A序列的长度小于图中点的数量,则说明某些节点未被遍历,进而说明图中存…...

【2022.1.3】手脱压缩壳练习(含练习exe)
【2022.1.3】手脱压缩壳练习(含练习exe) 文章目录【2022.1.3】手脱压缩壳练习(含练习exe)0、简介1、单步跟踪法(#)方法介绍(0)练习exe下载(1)、查看源程序&am…...

【异或哈希】CF855 div3 F
感觉这道题跟之前有一题特别像,都是异或哈希感觉这种题应该很典,记录一下(66条消息) Codeforces Round #841 (Div. 2) and Divide by Zero【异或差分动态map维护】 2022 C. Even Subarrays_lamentropetion的博客-CSDN博客Problem - F - Codeforces题意&a…...

深度学习|改进两阶段鲁棒优化算法i-ccg
目录 1 主要内容 2 改进算法 2.1 CC&G算法的优势 2.2 i-CCG算法简介 3 结果对比 1 主要内容 自从2013年的求解两阶段鲁棒优化模型的列和约束生成算法(CC&G)被提出之后,基本没有实质性的创新,都是围绕该算法在各个领…...

C++11轻松打印本地时间
C11之前,想要获取时间并对其打印是有些困难的,因为C并没有标准时间库。想要对时间进行统计就需要调用C库,并且我们要考虑这样的调用是否能很好的封装到我们的类中。 C11之后,STL提供了 chrono 库,其让对时间的操作更加…...
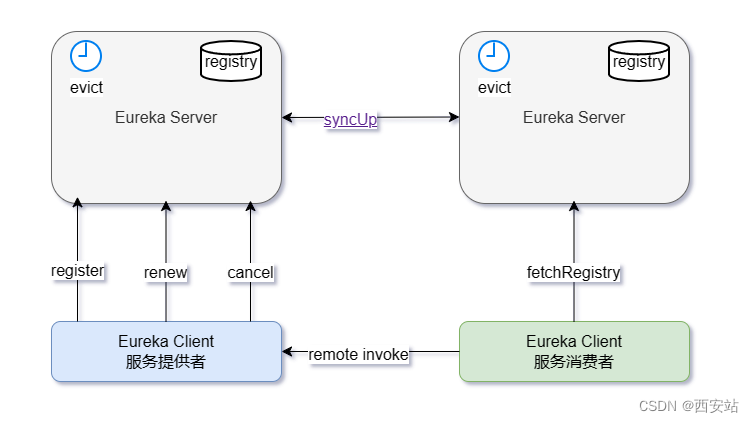
Eureka - 总览
文章目录前言架构注册中心 Eureka Server服务提供者 Eureka Client服务消费者 Eureka Client总结资源前言 微服务(Microservices,一种软件架构风格)核心的组件包括注册中心,随着微服务的发展,出现了很多注册中心的解决…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
