02 分解质因子
一、数n的质因子分解
题目描述:
输入一个数n(n<=10^6),将数n分解质因数,并按照质因数从小到大的顺序输出每个质因数的底数和指数。
输入 5
输出 5 1
输入 10
输出 2 1 5 1
朴素解法:
首先求出1~n的所有质数,每个质数每个质数的进行去除,要保证n中除尽除完,直到把n除到1为止。
程序实现:
#include<bits/stdc++.h>using namespace std;const int N=1e6;int prime[N],idx;
bool st[N];void init(){for(int i=2;i<N;i++){if(!st[i]) prime[++idx]=i;for(int j=1;prime[j]*i<N;j++){st[prime[j]*i]=1;if(i%prime[j]==0) break;}}
}
int main(){init();int n;cin>>n;if(!st[n]) cout<<n<<" "<<1<<endl;else{for(int i=1;prime[i]<=n&&i<=idx;i++){int p=prime[i];int sum=0;while(n%p==0){sum++;n/=p;}if(sum) cout<<p<<" "<<sum<<endl;}}return 0;
}优化思路:
其一:n如果除掉了前面的某个质因子,后面不能再被某个质因子的倍数整除了,证明比较简单,使用反证法就可以。
其二:n中最多只含有一个大于的因子。证明通过反证法:如果有两个大于sqrt(n)的因子,那么相乘会大于n,矛盾。证毕
基于上面的两条结论,只要从1~把每个数都除一遍,除尽除完,最后剩下的数如果不为1,这个数就是最大的质因子
代码实现
#include<bits/stdc++.h>
using namespace std;int main(){int n;cin>>n;for(int i=2;i<=n/i;i++){int sum=0;while(n%i==0){sum++;n/=i;}if(sum) cout<<i<<" "<<sum<<endl;}if(n!=1) cout<<n<<" "<<1<<endl;return 0;
}二、阶乘的质因子分解
题目描述
 题目分析:
题目分析:
我们枚举1∼n的所有数,把每一个数的质因子加到一个数组里。
最后输出质因子数量大于0的数。 时间复杂度为O(n^2/ln n)
程序实现:
#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
int prime[N],idx;
bool st[N];void init(){for(int i=2;i<N;i++){if(!st[i]) prime[++idx]=i;for(int j=1;prime[j]*i<N;j++){st[prime[j]*i]=1;if(i%prime[j]==0) break;}}
}
int ans[N]; //ans[i]表示第i个质因子的个数
int main(){init();int n;cin>>n;for(int i=2;i<=n;i++){ //枚举每一个数for(int j=1;prime[j]<=i&&j<=idx;j++){int p=prime[j];int cur=i;while(cur%p==0){ans[j]++;cur/=p;}}}for(int i=1;i<=idx;i++){if(ans[i]) cout<<prime[i]<<" "<<ans[i]<<endl;}return 0;
}优化思路:
我们不去枚举每个数,而是枚举每个质因子,看下在2~n中每个质因子出现的次数
在1x2x3x4x5x6x......x n-1 x n其中
能够被2整除的数有:
1*2 2*2 3*2....... i*2 其中2*i<=n 个数 i=n/2
能够被整除的数有:
1* 2*
3*
......i*
其中i*
<=n 个数i=n/
...........
在统计被2整除的个数时,相当于把每个数都除了2,剩下的数还有可能被2整除那些数是的数,
的数有n/
个,剩下的数还有可能被2整除,那些数是
的数,
的数有n/
个,............所以2作为因子的个数为
其中
同理3作为因子的个数为:
其中
等等
所以只要枚举每个质数,使用循环在求出该质数作为因子的个数即可,每个质数求解时,
p=,质数的个数为
,因此总的时间复杂度为
*
=
*
=
,即时间复杂度为O(n)
相关文章:
02 分解质因子
一、数n的质因子分解 题目描述: 输入一个数n(n<10^6),将数n分解质因数,并按照质因数从小到大的顺序输出每个质因数的底数和指数。 输入 5 输出 5 1 输入 10 输出 2 1 5 1 朴素解法: 首先求出1~n的所有质数…...

科技赋能智慧水利——山海鲸软件水利方案解析
作为山海鲸可视化软件的开发者,我们深感荣幸能为我国智慧水利建设提供强大助力。作为钻研数字孪生领域的开创者,我们希望不仅能为大家带来免费好用,人人都能用起来的数字孪生产品,还希望以其独特的技术优势和创新设计理念…...

C4.5决策树的基本建模流程
C4.5决策树的基本建模流程 作为ID3算法的升级版,C4.5在三个方面对ID3进行了优化: (1)它引入了信息值(information value)的概念来修正信息熵的计算结果,以抑制ID3更偏向于选择具有更多分类水平…...
)
本科毕业设计过程中应该锻炼的能力 (深度学习方向)
摘要: 本文以本科毕业设计做深度学习方向, 特别是全波形反演为例, 描述学生应在此过程中锻炼的能力. 搭建环境的能力. 包括 Python, PyTorch 等环境的安装.采集数据的能力. 包括 OpenFWI 等数据集.查阅资料的能力. 包括自己主要参考的文献, 以及其它相关文献 (不少于 20 篇). …...

深度学习——pycharm远程连接
目录 远程环境配置本地环境配置(注意看假设!!!这是很多博客里没写的)步骤1步骤2步骤2.1 配置Connection步骤2.2 配置Mappings 步骤3 配置本地项目的远程解释器技巧1 pycharm中远程终端连接技巧2 远程目录技巧3 上传代码文件技巧4 …...

信号量机制解决经典同步互斥问题
生产者 / 消费者问题、读者 / 写者问题和哲学家问题是操作系统的三大经典同步互斥问题。本文将介绍这三个问题的基本特点以及如何用信号量机制进行解决。 在分析这三个问题之前,我们首先需要了解用信号量机制解决同步互斥问题的一般规律: 实现同步与互斥…...
的区别,附代码举例)
java基础09-==和equals()的区别,附代码举例
和equals()的区别 在Java中,和equals()是两个不同的运算符,它们在比较对象时有着本质的区别。 运算符: 用于比较两个基本数据类型(如int、char等)或两个对象的引用。 当用于比较基本数据类型时,它会比较它们的值。 当…...
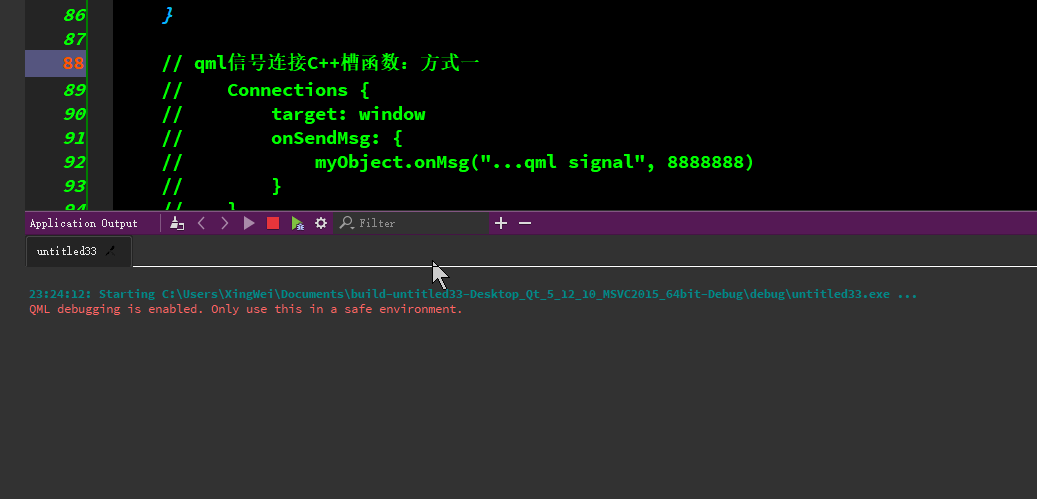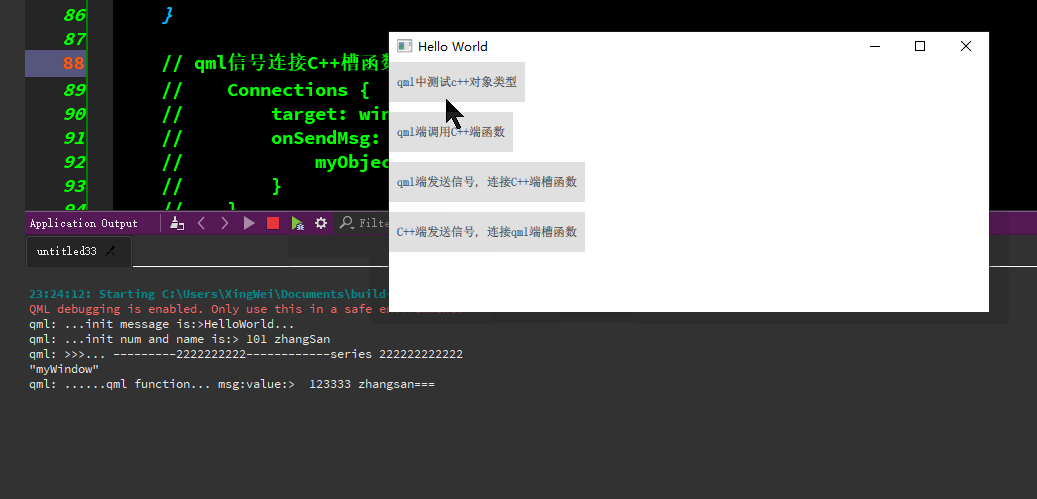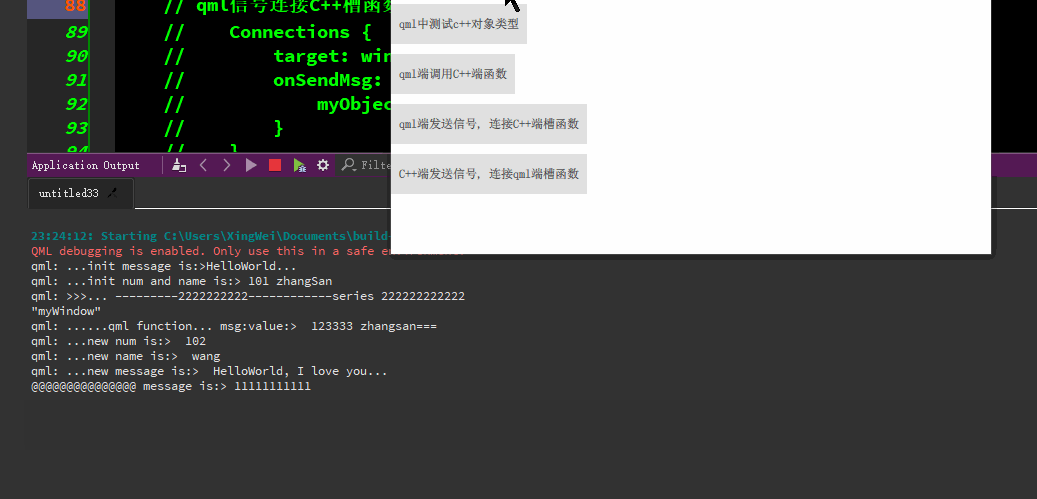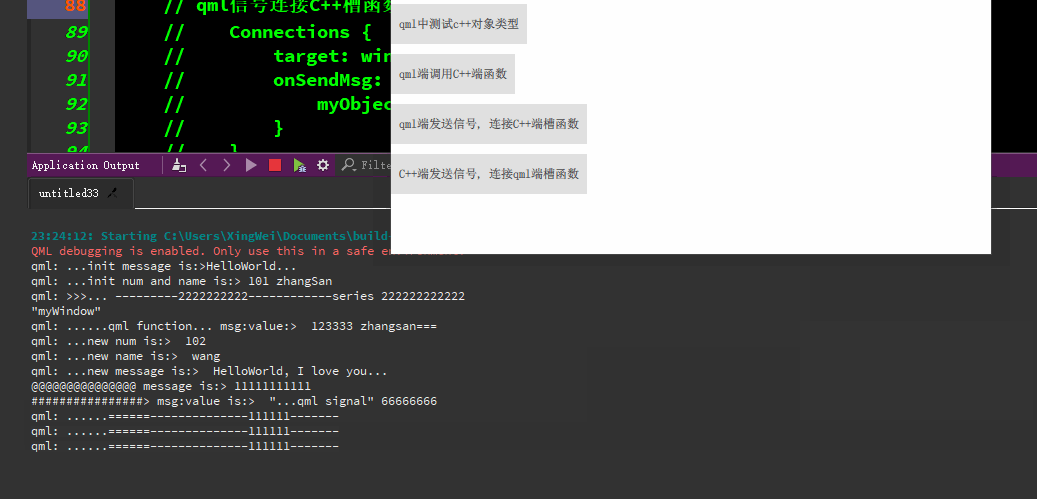
qml与C++的交互
qml端使用C对象类型、qml端调用C函数/c端调用qml端函数、qml端发信号-连接C端槽函数、C端发信号-连接qml端函数等。 代码资源下载: https://download.csdn.net/download/TianYanRen111/88779433 若无法下载,直接拷贝以下代码测试即可。 main.cpp #incl…...
LabVIEW电路板插件焊点自动检测系统
LabVIEW电路板插件焊点自动检测系统 介绍了电路板插件焊点的自动检测装置设计。项目的核心是使用LabVIEW软件,开发出一个能够自动检测电路板上桥接、虚焊、漏焊和多锡等焊点缺陷的系统。 系统包括成像单元、机械传动单元和软件处理单元。首先,利用工业相…...
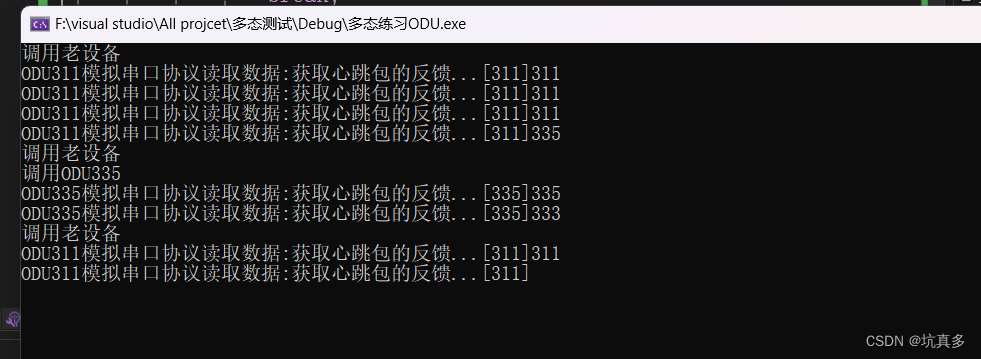
第十一站:多态练习ODU
实现动态切换 ODU.h #pragma once #include <iostream> using namespace std; #define ODU_TYPE_311_FLAG "311" #define ODU_TYPE_335_FLAG "335" enum class ODU_TYPE {ODU_TYPE_311,ODU_TYPE_335,ODU_TYPE_UNKNOW };class ODU{ public:ODU();//发…...

【深度学习】详解利用Matlab和Python中 LSTM 网络实现序列分类
🔗 运行环境:Matlab、Python 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 🔐#### 防伪水印——左手の明天 ####🔐 💗 大家好🤗🤗🤗,我是左手の明天!好久不见💗 💗今天分享Matlab深度学习—— LSTM 网络实现序列分...

Unity 工厂方法模式(实例详解)
文章目录 在Unity中,工厂方法模式是一种创建对象的常用设计模式,它提供了一个接口用于创建对象,而具体的产品类是由子类决定的。这样可以将对象的创建过程与使用过程解耦,使得代码更加灵活和可扩展。 工厂模式的主要优点如下&…...

2024年美赛数学建模思路 - 案例:异常检测
文章目录 赛题思路一、简介 -- 关于异常检测异常检测监督学习 二、异常检测算法2. 箱线图分析3. 基于距离/密度4. 基于划分思想 建模资料 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 一、简介 – 关于异常…...

一键完成,批量转换HTML为PDF格式的方法,提升办公效率
在当今数字化的时代,HTML和PDF已经成为两种最常用的文件格式。HTML用于网页内容的展示,而PDF则以其高度的可读性和不依赖于平台的特性,成为文档分享和传播的首选格式。然而,在办公环境中,我们经常需要在这两种格式之间…...

【重点问题】攻击面发现及管理
Q1:在使用长亭云图极速版时,是否需要增设白名单扫描节点? 长亭云图极速版高级网络安全产品基于一种理念,即攻击面发现是一个不断变换且需要持续对抗的过程。在理想的情况下,用户应当在所有预置防护设施发挥作用的环境…...

UE4外包团队:国外使用UE4虚幻引擎制作的十个知名游戏
1.俄罗斯方块效果(任天堂 Switch、PlayStation 4、PC、Xbox) 2.耀西的手工世界(任天堂 Switch) 3. Final Fantasy 7 Remake Intergrade (PlayStation, PC) 4.《堡垒之夜》(PC、Nintendo Switch、PlayStation、Xb…...
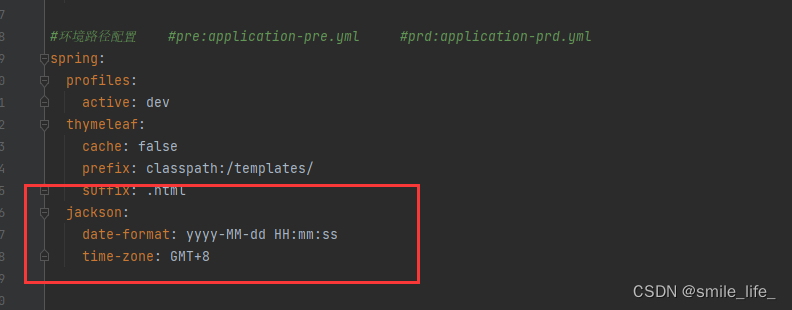
解决springboot+mybatisplus返回时间格式带T
原因:我service实现类的代码是 Overridepublic Map<String, Object> queryDictPage(Map<String, Object> queryMap) {Map<String,Object> map new HashMap<>();QueryWrapper<Dict> wrapper new QueryWrapper<>(); // …...
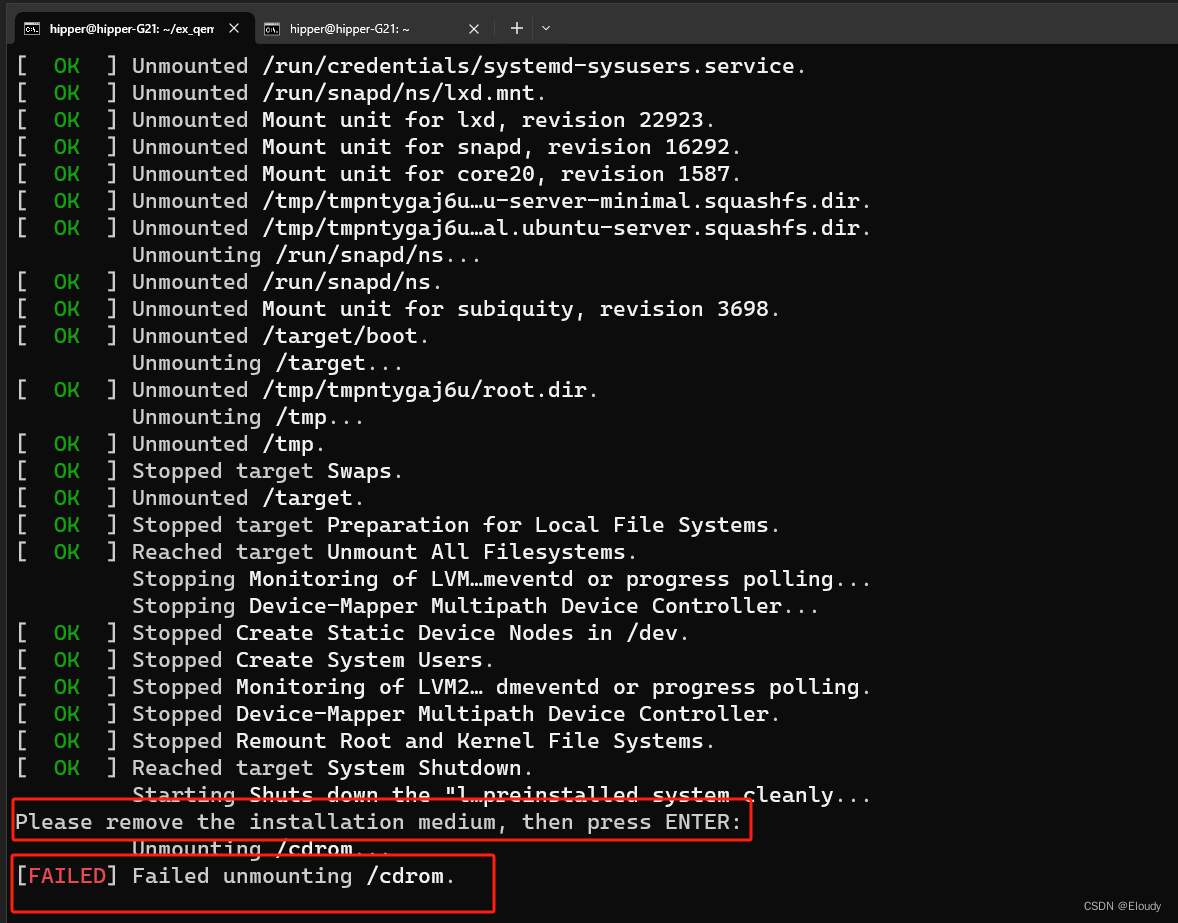
纯命令行在Ubuntu中安装qemu的ubuntu虚拟机,成功备忘
信息总体还算完整,有个别软件更新了名字,所以在这备忘一下 1. 验证kvm是否支持 ________________________________________________________________ $ grep vmx /proc/cpuinfo __________________________________________________________________…...

Vue的学习Day1_是什么以及两种风格
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、Vue是什么?二、渐进式框架1.渐进式 三、Vue API风格1.选项式 API (Options API)2.组合式 API (Composition API) 四、Vue 开发前的准备 前言 放…...
磁悬浮人工心脏的不良事件分析:美国FDA数据库的启示
引言: 左心室辅助装置(LVAD)是治疗末期难治性心力衰竭(HF)患者的有效手段。磁悬浮人工心脏HeartMate-3(磁悬浮人工心脏)作为第三代LVAD,自2017年获得美国食品药品监督管理局&#x…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
