PHP AES加解密系列
PHP AES加密
使用PHP内置的mcrypt扩展库可以轻松地实现AES加密。
<?php
function aes_encrypt($data, $key, $iv) {$cipher = mcrypt_module_open(MCRYPT_RIJNDAEL_128, '', MCRYPT_MODE_CBC, '');mcrypt_generic_init($cipher, $key, $iv);$encrypted = mcrypt_generic($cipher, $data);mcrypt_generic_deinit($cipher);mcrypt_module_close($cipher);return base64_encode($encrypted);
}$key = '1234567890abcdef';
$iv = 'fedcba0987654321';
$data = 'Hello World!';
$encrypted = aes_encrypt($data, $key, $iv);
echo $encrypted;
?>
PHP AES解密
使用PHP内置的mcrypt扩展库也可以轻松地实现AES解密。
<?php
function aes_decrypt($encrypted, $key, $iv) {$cipher = mcrypt_module_open(MCRYPT_RIJNDAEL_128, '', MCRYPT_MODE_CBC, '');mcrypt_generic_init($cipher, $key, $iv);$decrypted = mdecrypt_generic($cipher, base64_decode($encrypted));mcrypt_generic_deinit($cipher);mcrypt_module_close($cipher);return trim($decrypted);
}$key = '1234567890abcdef';
$iv = 'fedcba0987654321';
$encrypted = 'jRd3dw8c5YX2w/oQvhFqfg==';
$decrypted = aes_decrypt($encrypted, $key, $iv);
echo $decrypted;
?>
以上就是PHP AES加解密的简单实现方法。需要注意的是,mcrypt扩展库已经在PHP7.2版本中被废弃,建议使用其他扩展库或者使用PHP7.2以上版本内置的openssl扩展库实现AES加解密。
相关文章:

PHP AES加解密系列
PHP AES加密 使用PHP内置的mcrypt扩展库可以轻松地实现AES加密。 <?php function aes_encrypt($data, $key, $iv) {$cipher mcrypt_module_open(MCRYPT_RIJNDAEL_128, , MCRYPT_MODE_CBC, );mcrypt_generic_init($cipher, $key, $iv);$encrypted mcrypt_generic($ciphe…...
QT5数据库)
QT基础篇(13)QT5数据库
1.数据库基本概念 数据库(Database)是指存储、管理和组织数据的集合。它是一个组织化的、可持久化的数据集合,用于支持数据的存储、检索、更新和管理。 数据库系统(Database System)是建立在计算机上的数据管理系统&…...
ctfshow信息收集(web1-web20)
目录 web1 web2 web3 web4 web5 web6 web7 web9 web10 web11 web14 web15 web16 web17 web18 web19 web20 web1 根据提示的孩子开发的时候注释没有被及时删除 web2 js原因无法查看源代码 第一种方法 在url前加入 view-source: 会显示页面源代…...

从零学习Hession RPC
为什么学习Hessian RPC? 存粹的RPC,只解决PRC的四个核心问题(1.网络通信2.协议 3.序列化 4.代理)Java写的HessianRPC落伍了,但是它的序列化方式还保存着,被Dubbo(Hessian Lite)使用。 被落伍,只…...

实施精细化管理的六大关键步骤
在当今高度竞争的市场环境中,企业若想脱颖而出,必须实现精细化管理。这不仅是为了提高效率,更是为了确保在复杂多变的市场中保持领先地位。通过以下六个关键步骤,企业可以构建一个强大的精细化管理体系,从而为未来的成…...

QT+C++环境调用python函数可以进入python环境和模块,但是调用功能函数错误
QTC环境使用Python.h调用python函数可以进入python环境和模块,但是调用功能函数错误 背景: 定义的python函数使用了其他库封装好的函数,在python环境下运行此程序毫无问题但是QT调用却显示调用此函数出错,此时调用此.py文件内的其…...

2024.1.24力扣每日一题——美丽塔I
2024.1.24 题目来源我的题解方法一 暴力枚举方法二 单调栈前、后缀和 题目来源 力扣每日一题;题序:2865 我的题解 方法一 暴力枚举 将每个位置都作为山峰来进行遍历,计算每个山峰下的最大山脉数组和 时间复杂度:O( n 2 n^2 n2)…...
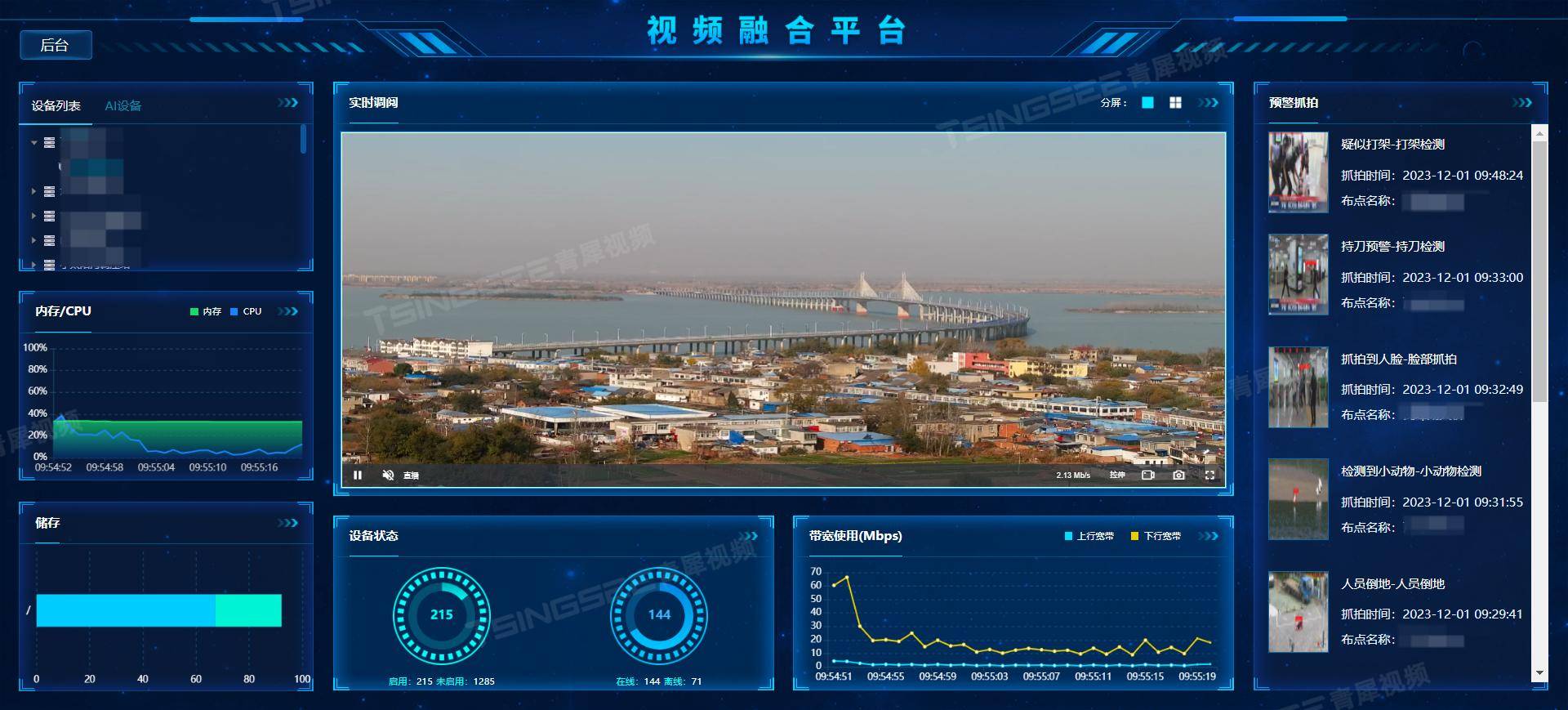
视频监控平台EasyCVR增加fMP4流媒体视频格式及其应用场景介绍
近期我们在视频监控管理平台EasyCVR系统中新增了HTTP-FMP4播放协议,今天我们就来聊聊该协议的特点和应用。 fMP4(Fragmented MPEG-4)是基于MPEG-4 Part 12的流媒体格式,是流媒体的一项重要技术,因为它能通过互联网传送…...

使用Python的pygame库实现迷宫游戏
使用Python的pygame库实现迷宫游戏 关于Python中pygame游戏模块的安装使用可见 https://blog.csdn.net/cnds123/article/details/119514520 先给出效果图: 这个游戏每次运行能自动随机生成迷宫布局。 在这个游戏中,玩家将使用键盘箭头键来移动&#x…...
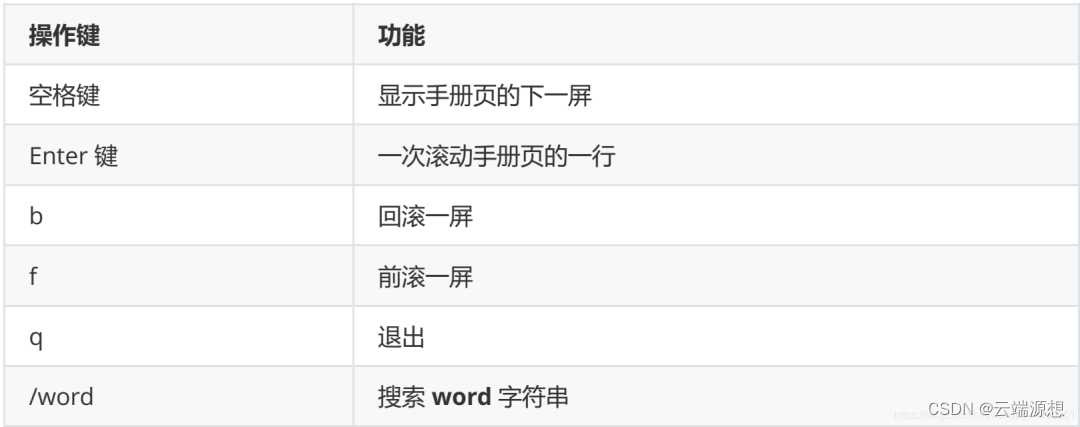
Linux新手村必备!这些常用操作命令你掌握了吗?
在计算机的世界里,Linux操作系统以其强大的功能和灵活性受到了广大程序员和IT爱好者的喜爱。然而,对于初学者来说,Linux的操作命令可能会显得有些复杂和难以理解。 今天,我们就来一起探索一些Linux常用操作命令,让你的…...
:iPad横屏适配)
ReactNative进阶(三十六):iPad横屏适配
文章目录 一、前言二、实现思路三、延伸阅读四、拓展阅读 一、前言 应用RN技术栈实现APP上线后,业务部门领导会上反馈未实现ipad横屏全屏展示,用户体验较差。由此,一场pad横屏全屏展示的APP调优工作由此开展。 二、实现思路 时间紧任务重&…...

jsx中使用插槽
1. jsx语法中使用插槽 以elementplus ElPopconfirm 为例 <el-popconfirm title"Are you sure to delete this?"><template #reference><el-button>Delete</el-button></template></el-popconfirm>使用 slots: {default: (dat…...

CentOS服务器拒绝SSH登录
当CentOS服务器拒绝SSH登录时,有几个可能的原因和解决方法: 检查网络连接:确保服务器与您的计算机之间的网络连接是正常的。您可以尝试使用其他网络连接或ping服务器以检查是否能够访问。 确认SSH服务正在运行:在服务器上确认SSH…...
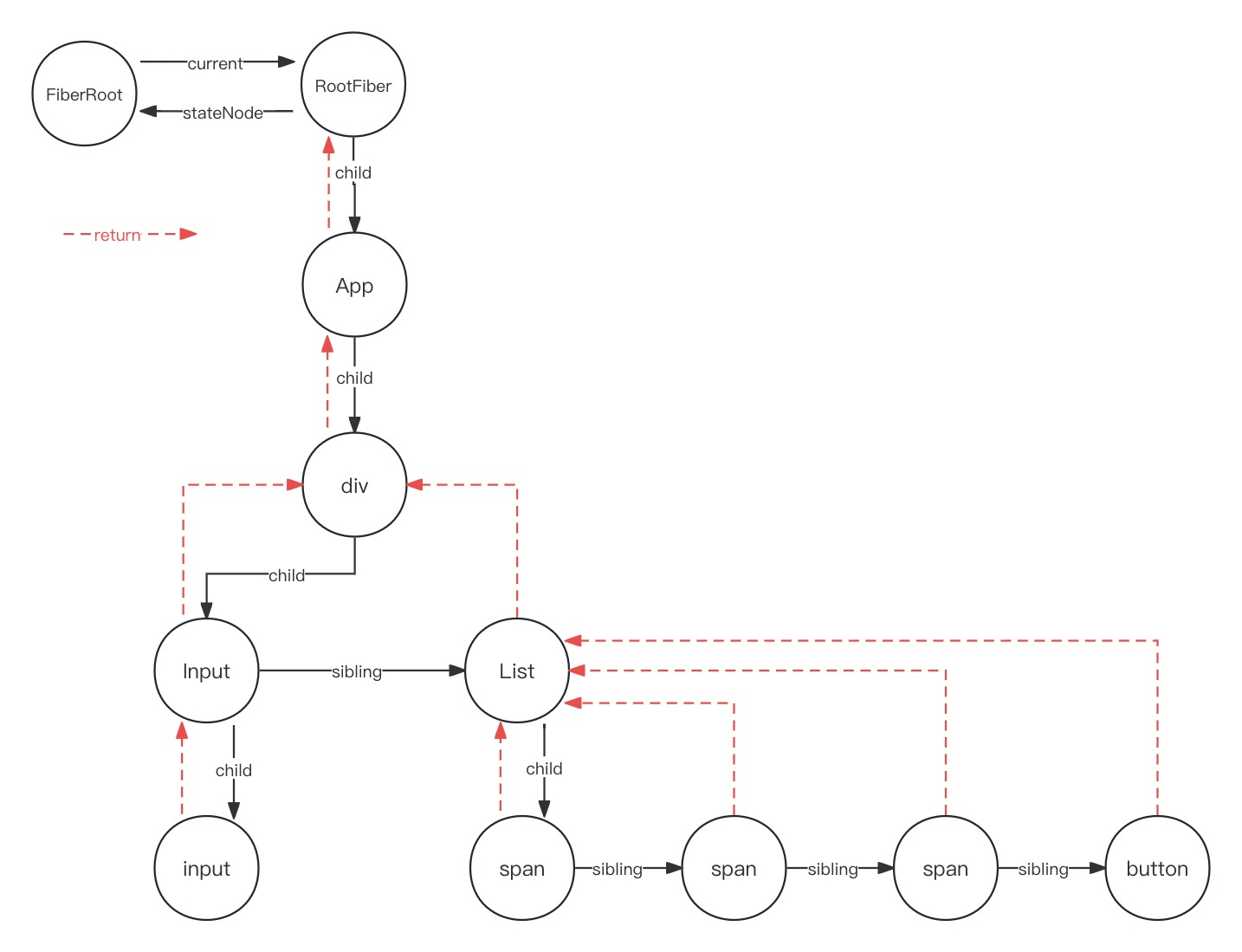
React16源码: React中的completeUnitOfWork的源码实现
completeUnitOfWork 1 )概述 各种不同类型组件的一个更新过程对应的是在执行 performUnitOfWork 里面的 beginWork 阶段它是去向下遍历一棵 fiber 树的一侧的子节点,然后遍历到叶子节点为止,以及 return 自己 child 的这种方式在 performUni…...

uniapp移动端——企业微信H5调用jssdk实现扫一扫,通过weixin-java-cp获取ticket签名,配置config
背景: 使用企业微信开发扫一扫功能 可信域名验证 (1)企业微信的可信域名需要和企业微信的备案主体一致。 域名备案主体可通过站长工具查看域名备案主体。https://icp.chinaz.com/ 企业微信备案主体可以咨询管理员 (2)通过nginx配置域名归…...

【前端基础--1】
为后面爬虫打基础 使用Visual Studio Code(VS Code) https://code.visualstudio.com/#alt-downloads 网页基础 创建一个html网页 新建一个文件 文件名后缀.html 书写网页模板 html:5 回车键(或者Tab键)英文感叹号! 回…...

E2 Mysql的基本操作和用户权限
一、实验目的: 要求掌握Mysql平台的基本操作和基本的权限管理。 二、实验要求: 1、基本硬件配置:英特尔Pentium III 以上,大于4G内存; 2、软件要求:Mysql; 3、时间:4小时; 4、撰写实验报告并按时提交。 三、实验内容: Group 1: 安装Mys…...
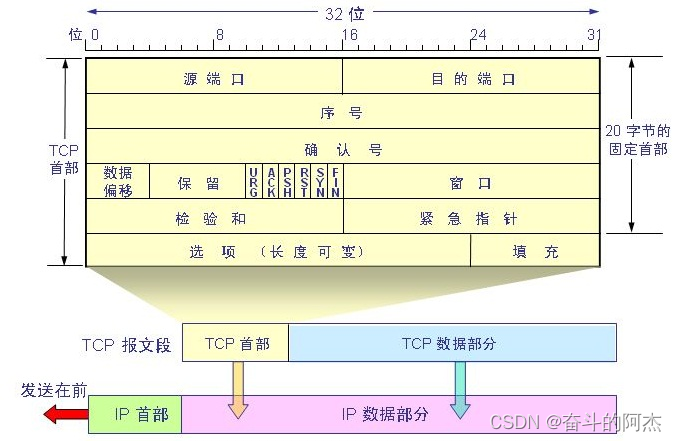
TCP 的三次握手和四次挥手
Java 面试题 TCP 三次握手 第一次握手:客户端向服务端发送SYN包。报文中标志位SYN1,序列号seqx(x为随机整数)。此时客户端进入了 SYN_SEND 同步已发送状态。 第二次握手:服务端回复客户端SYNACK包。报文中标志位SYN1&…...
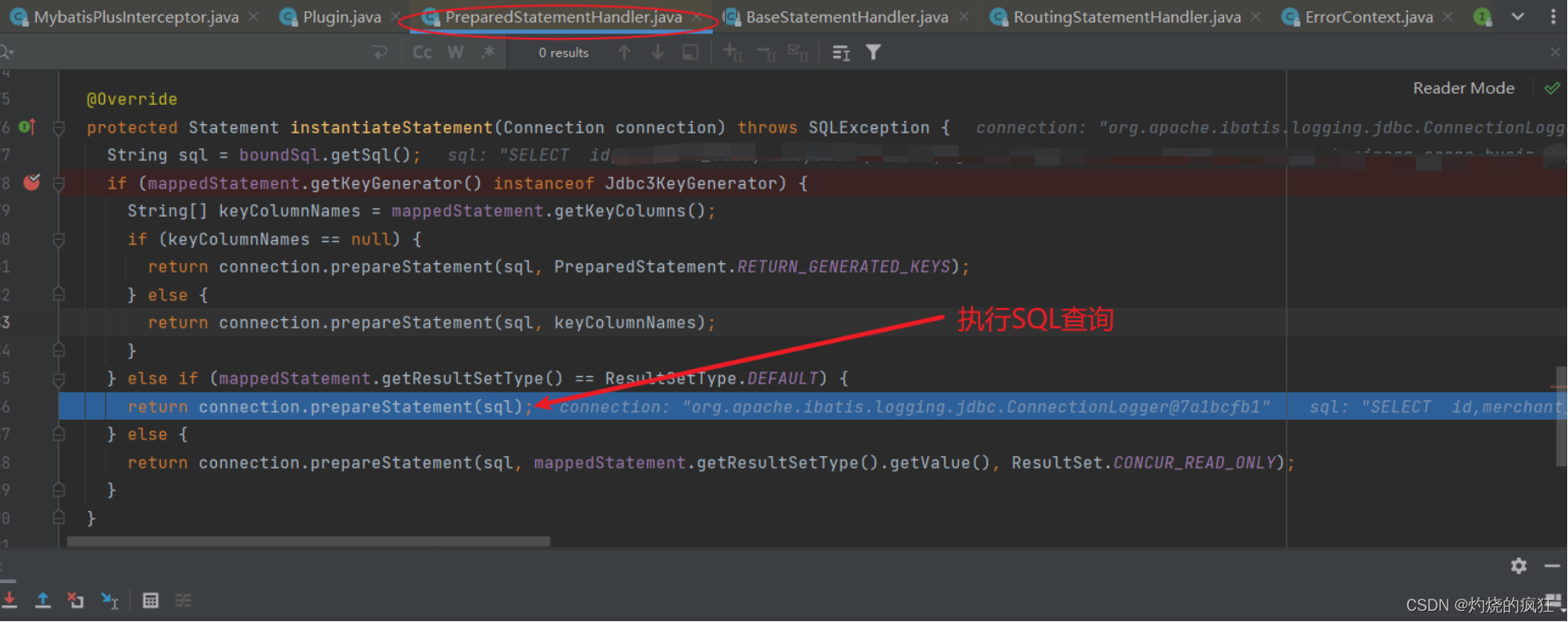
mybatisplus做SQL拦截添加自定义排序
前言 工作中写的一段代码,备个份,以后兴许能直接用 功能描述:如果前端传入了排序规则,则优先按传入的字段进行排序,SQL原有的排序规则追加到末尾 注:我们项目里的分页查询,是基于XML的SQL执行的…...

代码随想录算法训练营第29天(回溯算法05 | * 491.递增子序列 * 46.全排列 * 47.全排列 II
回溯算法part05 491.递增子序列解题思路与 90.子集II 不同的点回溯三部曲 46.全排列解题思路遇到的难点思考 47.全排列 II解题思路注意点拓展需要加深理解的点(需复习 小总结 491.递增子序列 本题和大家刚做过的90.子集II非常像,但又很不一样,…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
