从动力系统研究看当今数学界
§6.3... Milnor’s definition of “attractors” which has been criticized above by us).
The work of [KSS2] of asserting the existence of “nice open set” of Ω(p.148) would be likely not verified, for example we think the first sentence “… since f is nontrivial, it has infinitely many periodic orbit…” in deducing Lemma 6.1 of [KSS1] needs to be explained. In [K1](p.748, the last paragraph) the author talked the existence of “nice intervals”, but we think his assertion would be only verified for certain quadratic-polynomial mappings, whereas [K1] is under certain general settings(see also [K2], p.7). ...
§6.5 We think the “Axiom A mappings” may not exist, because such mappings are required that “all periodic points are hyperbolic” which cannot be verified in general(see p.302 of [S]), and thus all involved works would be in vain.
[K1]O.Kozlovski, Getting rid of the negative Schwarzian derivative condition, Ann.of Math.152(2000),743-762.
[K2]O.Kozlovski, Axiom A mappings are dense in the space of unimodal maps in the
topology, ibid, 157(2003), 1-43.
[KSS1]O.Kozlovski, W,Shen and S.v.Strien, Rigidity for real oplynomials, ibid,165(2007), 749-841.
[KSS2]O.Kozlovski, W,Shen and S.v.Strien, Density of hyperbolicity in dimension one, ibid, 166(2007), 145-182.
[S]W.Shen, On the metric properties of multimodal interval maps and density of Axiom A, Invent. Math. 156(2004), 301-403.
----------------------------------------------------------
以上摘自我对动力系统方面工作的批判(在整个分析学的批判中列在§6)。从中发现一些实质错误,并看出沈维孝早在2004年(29岁)就已经在顶级刊物发表一篇100多页的论文,但也仅在国内弄到陈省身奖,在国际数学界似乎没啥名气,跟他合作的斯拉夫人O.Kozlovski似乎也类似。原因很简单,每年在几个国际顶级数学刊物发表论文的几百人,不可能都在国际数学界享有很高地位。更看出,沈维孝似乎已经参评院士4次都落空(从2004年起),算今年第5次,这反映了国内数学宗派主义很严重。剑桥大学三一学院的Alan Baker就是31岁获得Fields奖的。
相关文章:

从动力系统研究看当今数学界
6.3... Milnor’s definition of “attractors” which has been criticized above by us). The work of [KSS2] of asserting the existence of “nice open set” of Ω(p.148) would be likely not verified, for example we think the first sentence “… since f is nont…...
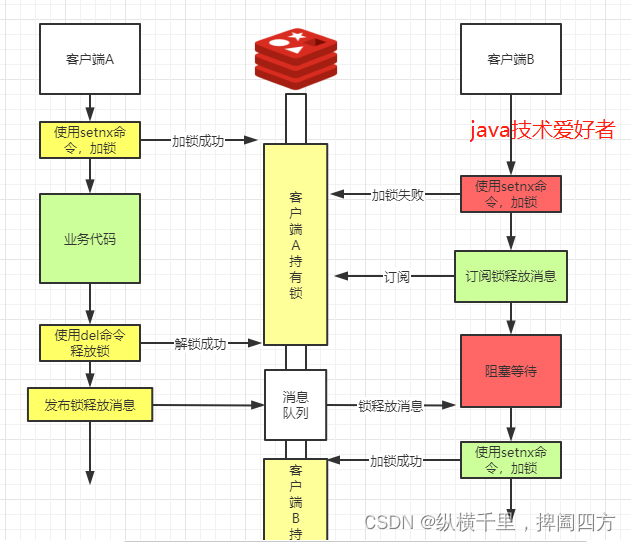
【征服redis15】分布式锁的功能与整体设计方案
目录 1. 分布式锁的概念 2.基于数据库做分布式锁 2.1 基于表主键唯一做分布式锁 2.2 基于表字段版本号做分布式锁 2.3 基于数据库排他锁做分布式锁 3.使用Redis做分布式锁 3.1 redis实现分布式锁的基本原理 3.2 问题一:增加超时机制,防止长期持有…...

MATLAB中实现机械臂逆运动学求解的方法之一是使用阻尼最小二乘法
MATLAB中实现机械臂逆运动学求解的方法之一是使用阻尼最小二乘法。阻尼最小二乘法通常用于处理数值求解问题中的不稳定性和噪声。以下是一个简单的MATLAB代码示例,演示了机械臂逆运动学的阻尼最小二乘法求解: % 机械臂参数 L1 1; % 机械臂长度 L2 1;…...
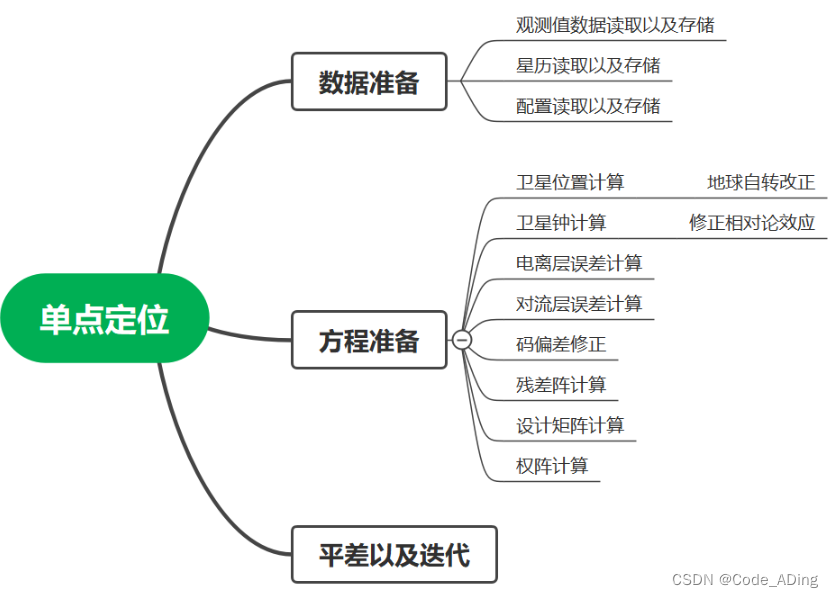
2024.1.24 GNSS 学习笔记
1.伪距观测值公式 2.载波相位观测值公式 3.单点定位技术(Single Point Positionin, SPP) 仅使用伪距观测值,不使用其他的辅助信息获得ECEF框架下绝对定位技术。 使用广播星历的轨钟进行定位,考虑到轨钟的米级精度,所以对于<1米的误差&…...
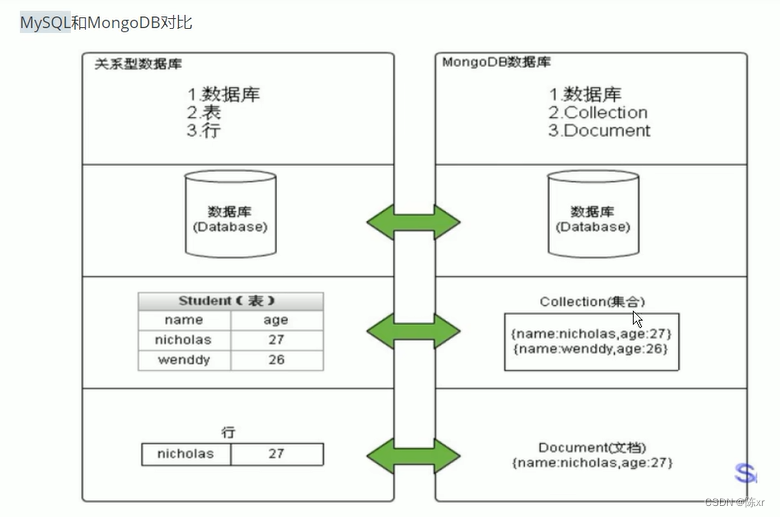
2024-01-22(MongoDB)
1.Mongodb使用的业务场景: 传统的关系型数据库/mysql在“三高”需求以及应对web2.0的网站需求面前,有点力不从心,什么是“三高”需求: a. 对数据库高并发的读写需求 b. 对海量数据的高效率存储和访问需求 c. 对数据库的高可扩…...
无人机航迹规划(六):七种元启发算法(DBO、LO、SWO、COA、LSO、KOA、GRO)求解无人机路径规划(提供MATLAB代码)
一、七种算法(DBO、LO、SWO、COA、LSO、KOA、GRO)简介 1、蜣螂优化算法DBO 蜣螂优化算法(Dung beetle optimizer,DBO)由Jiankai Xue和Bo Shen于2022年提出,该算法主要受蜣螂的滚球、跳舞、觅食、偷窃和繁…...
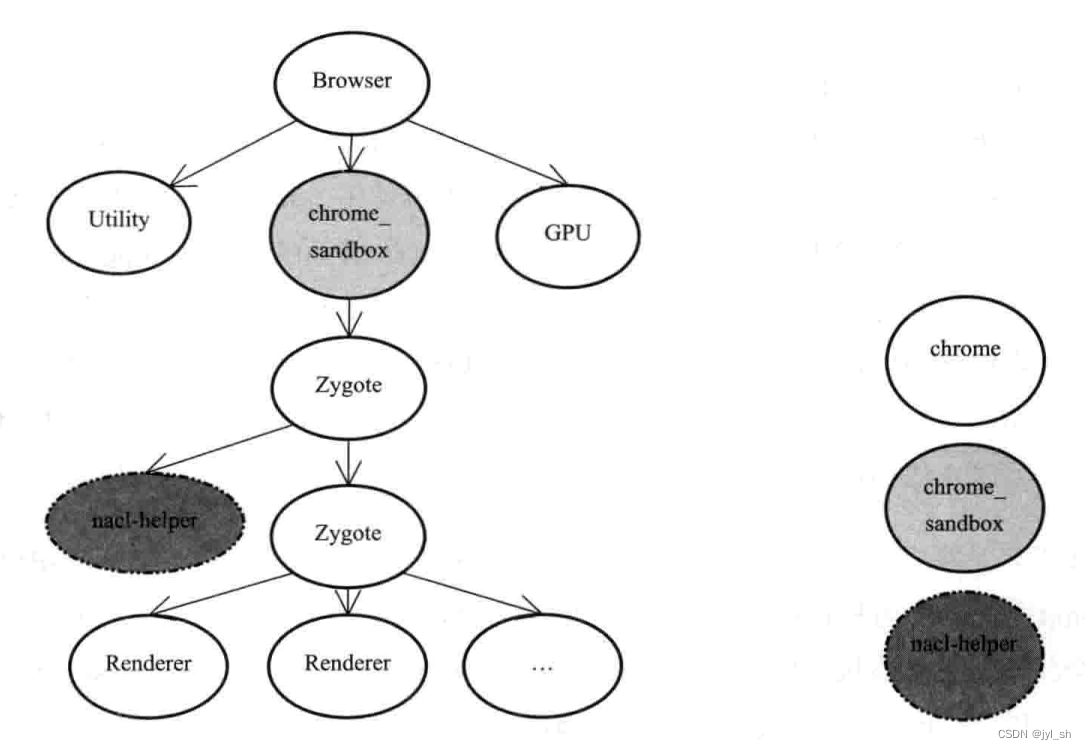
《WebKit 技术内幕》学习之十二(2):安全机制
2 沙箱模型 2.1 原理 一般而言,对于网络上的网页中的JavaScript代码和插件是不受信的(除非是经过认证的网站),特别是一些故意设计侵入浏览器运行的主机代码更是非常危险,通过一些手段或者浏览器中的漏洞,…...
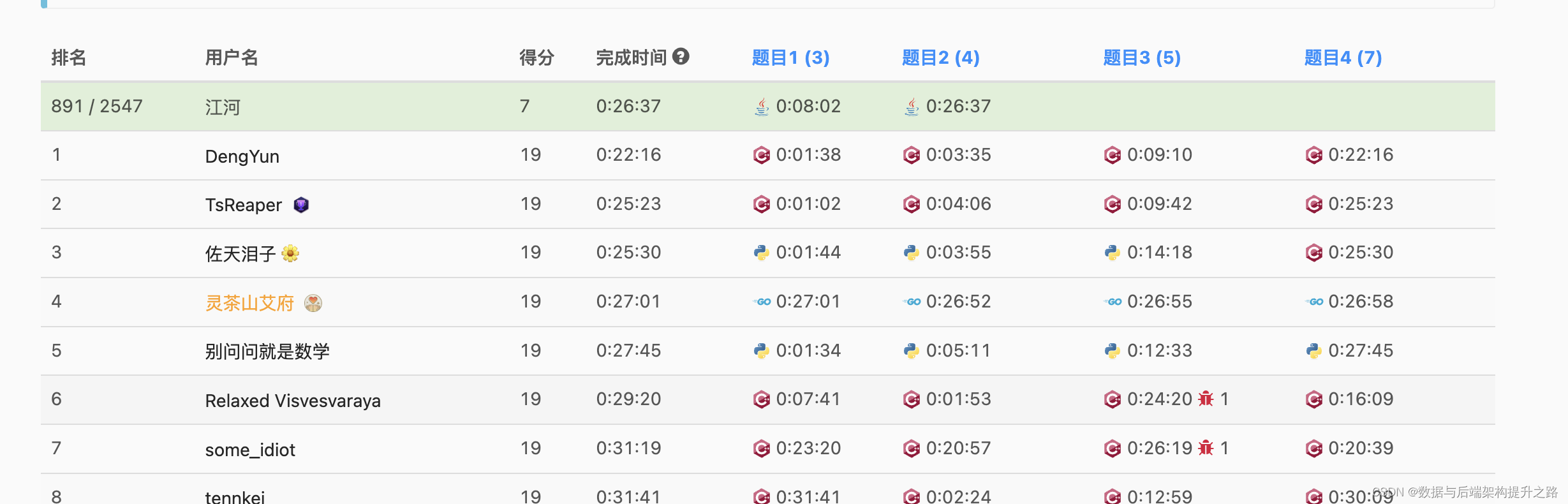
算法优化:LeetCode第122场双周赛解题策略与技巧
接下来会以刷常规题为主 ,周赛的难题想要独立做出来还是有一定难度的,需要消耗大量时间 比赛地址 3011. 判断一个数组是否可以变为有序 public class Solution {public int minimumCost(int[] nums) {if (nums.length < 3) {// 数组长度小于3时&a…...
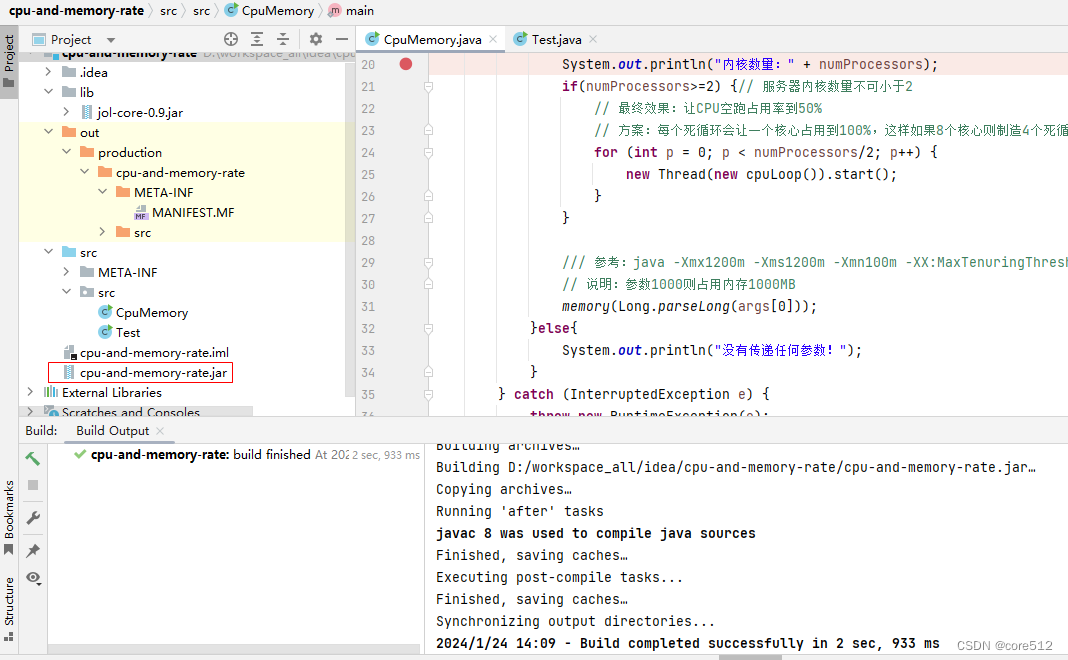
IDEA导出jar
1、选择导出方式 2、选择Main Class 3、构建jar...
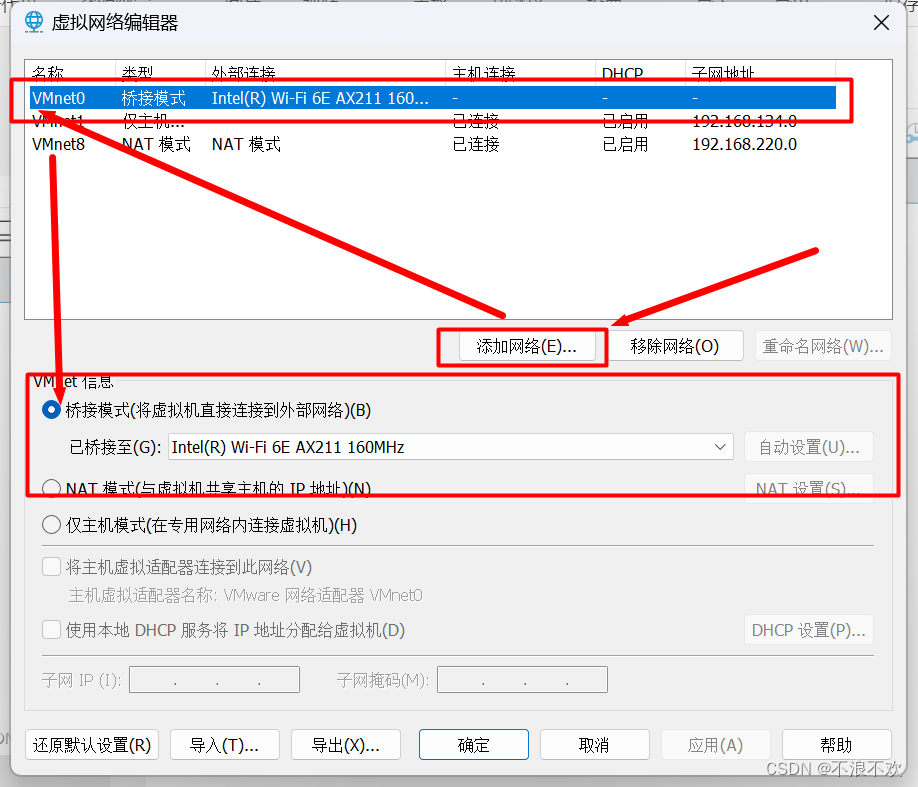
Win10/11中VMware Workstation设置网络桥接模式
文章目录 一、添加VMware Bridge Protocol服务二、配置桥接参数1.启用系统Device Install Service服务2.配置VMware 需要确认物理网卡是否有添加VMware Bridge Protocol服务 添加VMware Bridge Protocol服务 提示:以下是本篇文章正文内容,下面案例可供参…...

html Canvas粒子文字特效
代码有点长,下面是代码: <!DOCTYPE html> <html><head><meta charset"UTF-8"><title>HTML5 Canvas粒子效果文字动画特效DEMO演示</title><link rel"stylesheet" href"css/normalize.c…...

@JsonFormat失效,被jackson自定义配置覆盖
jackson配置类 我的jackson配置类如下,其中serializerByType(LocalDateTime.class, new LocalDateTimeSerializer()) 覆盖了JsonFormat注解 Configuration public class JacksonConfiguration {public static final DateTimeFormatter optionalDateTimePattern (n…...
SaaS系统如何助力企业数字化转型
随着科技的快速发展,数字化转型已经成为企业适应市场变化、提高竞争力的必要手段。在这个过程中,SaaS(软件即服务)系统以其独特的优势,正在成为越来越多企业的首选。乔拓云SaaS系统作为这一领域的佼佼者,更…...
nginx配置内网代理,前端+后端分开配置
安装好后nginx,进入配置文件 我这块安装在了home里面,各位根据自身情况选择 打开nginx.conf文件 在底部查看是否包含这段信息:含义是配置文件包含该路径下的配置文件 include /home/nginx/conf/conf.d/*.conf; # 该路径根据自己的安装位置自行修改 配置文件 进入conf.d文…...
i18n多国语言Internationalization的动态实现
一、数据动态的更新 在上一篇i18n多国语言Internationalization的实现-CSDN博客,可能会遇到一个问题,我们在进行英文或中文切换时,并没有办法对当前的数据进行动态的更新。指的是什么意思呢?当前app.js当中一个组件内容ÿ…...
C++笔记(二)
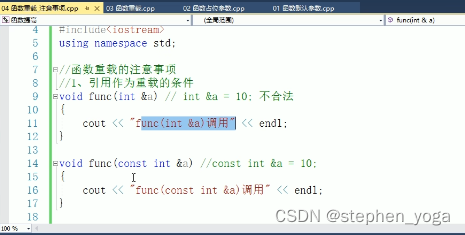
函数的默认参数 如果我们自己传入数据,就用自己的数据,如果没有,就用默认值 语法: 返回值类型 函数名(形参默认值){} int func(int a,int b20,int c30){} …...

【技能---构建github中SSH密钥的流程】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言SSH基于账号口令的安全验证通过SSH连接到服务器打开终端(命令行界面)使用 SSH 命令连接: 在 Ubuntu 中生成 SSH 密钥并将其添…...

linux-centos服务器离线安装yapi(包含nodejs、mongodb、yapi、pm2离线安装)
yapi是使用vue框架开发的,借助nodejs 前端直接访问的mongodb数据库,离线安装yapi步骤如下 下载离线安装包 下载地址 https://download.csdn.net/download/qq445829096/88778418 离线安装包先复制到 dev/yapi目录(根据自己习惯自定义目录) node-v12.13.0-linux-x64.tar.xz …...

手撕重采样,考虑C的实现方式
一、参考文章: 重采样、上采样、下采样 - 知乎 (zhihu.com) 先直接给结论,正常重采样过程如下: 1、对于原采样率fs,需要重采样到fs1,一般fs和fs1都是整数哈,则先找fs和fs1的最小公倍数,设为m…...

网络安全产品之认识入侵防御系统
由于网络安全威胁的不断演变和增长。随着网络技术的不断发展和普及,网络攻击的种类和数量也在不断增加,给企业和个人带来了巨大的安全风险。传统的防火墙、入侵检测防护体系等安全产品在面对这些威胁时,存在一定的局限性和不足,无…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...
