力扣1027. 最长等差数列
动态规划
- 思路:
- 可以参考力扣1218. 最长定差子序列
- 目前不清楚公差,可以将序列最大最小值找到,公差的范围是 [-(max - min), (max - min)],按公差递增迭代遍历求出最长等差数列;
class Solution {
public:int longestArithSeqLength(vector<int>& nums) {auto [minit, maxit] = std::minmax_element(nums.begin(), nums.end());int diff = *maxit - *minit;int ans = 0;for (int d = -diff; d <= diff; ++d) {std::unordered_map<int, int> dp;for (int v : nums) {dp[v] = dp[v - d] + 1;ans = std::max(ans, dp[v]);}}return ans;}
};- 时间复杂度比较高,应该是哈希表频繁插入导致,将 dp 数据结构换成数组,数组下标最大值为元素最大值 + 1;
class Solution {
public:int longestArithSeqLength(vector<int>& nums) {auto [minit, maxit] = std::minmax_element(nums.begin(), nums.end());int diff = *maxit - *minit;int ans = 1;for (int d = -diff; d <= diff; ++d) {std::vector<int> dp(*maxit + 1, -1);for (int v : nums) {int prev = v - d;// ensure prev is in nums and has exist(or v is the first item)if (prev >= *minit && prev <= *maxit && dp[prev] != -1) {dp[v] = std::max(dp[v], dp[prev] + 1);ans = std::max(ans, dp[v]);}dp[v] = std::max(dp[v], 1);}}return ans;}
};——————————————————————————————

相关文章:

力扣1027. 最长等差数列
动态规划 思路: 可以参考力扣1218. 最长定差子序列目前不清楚公差,可以将序列最大最小值找到,公差的范围是 [-(max - min), (max - min)],按公差递增迭代遍历求出最长等差数列; class Solution { public:int longest…...
)
GraphicsMagick 的 OpenCL 开发记录(二十三)
文章目录 ImageMagick和GraphicsMagick函数及宏对照表 <2022-04-14 周四> ImageMagick和GraphicsMagick函数及宏对照表 在开发过程中收集了这两个项目中的一些相同或相似功能的函数或者宏定义,希望对大家有所帮助,如下: TypeImageMa…...
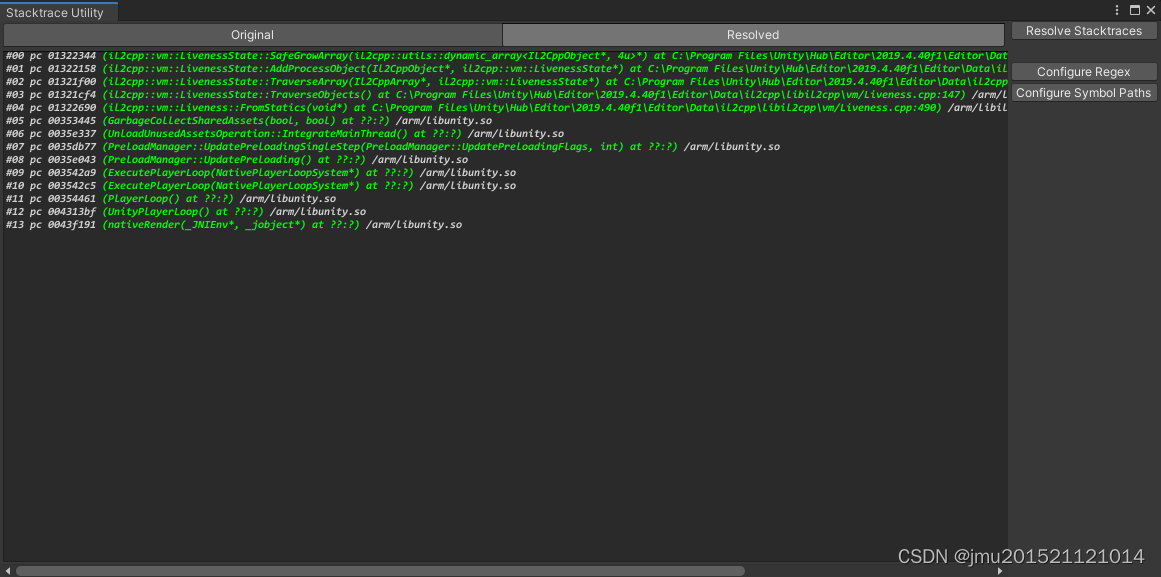
通过Android Logcat分析firebase崩溃
参考:UnityIL2CPP包Crash闪退利用Android Logcat还原符号表堆栈日志 - 简书 一、安装Android Logcat插件 1、新建空白unity工程,打开PackageManager窗口,菜单栏Window/PackageManager 2、PackageManager中安装Android Logcat日志工具 3、安…...

【AI大模型】WikiChat超越GPT-4:在模拟对话中事实准确率提升55%终极秘密
WikiChat,这个名字仿佛蕴含了无尽的智慧和奥秘。它不仅是一个基于人工智能和自然语言处理技术的聊天机器人,更是一个能够与用户进行深度交流的智能伙伴。它的五个突出特点:高度准确、减少幻觉、对话性强、适应性强和高效性能,使得…...
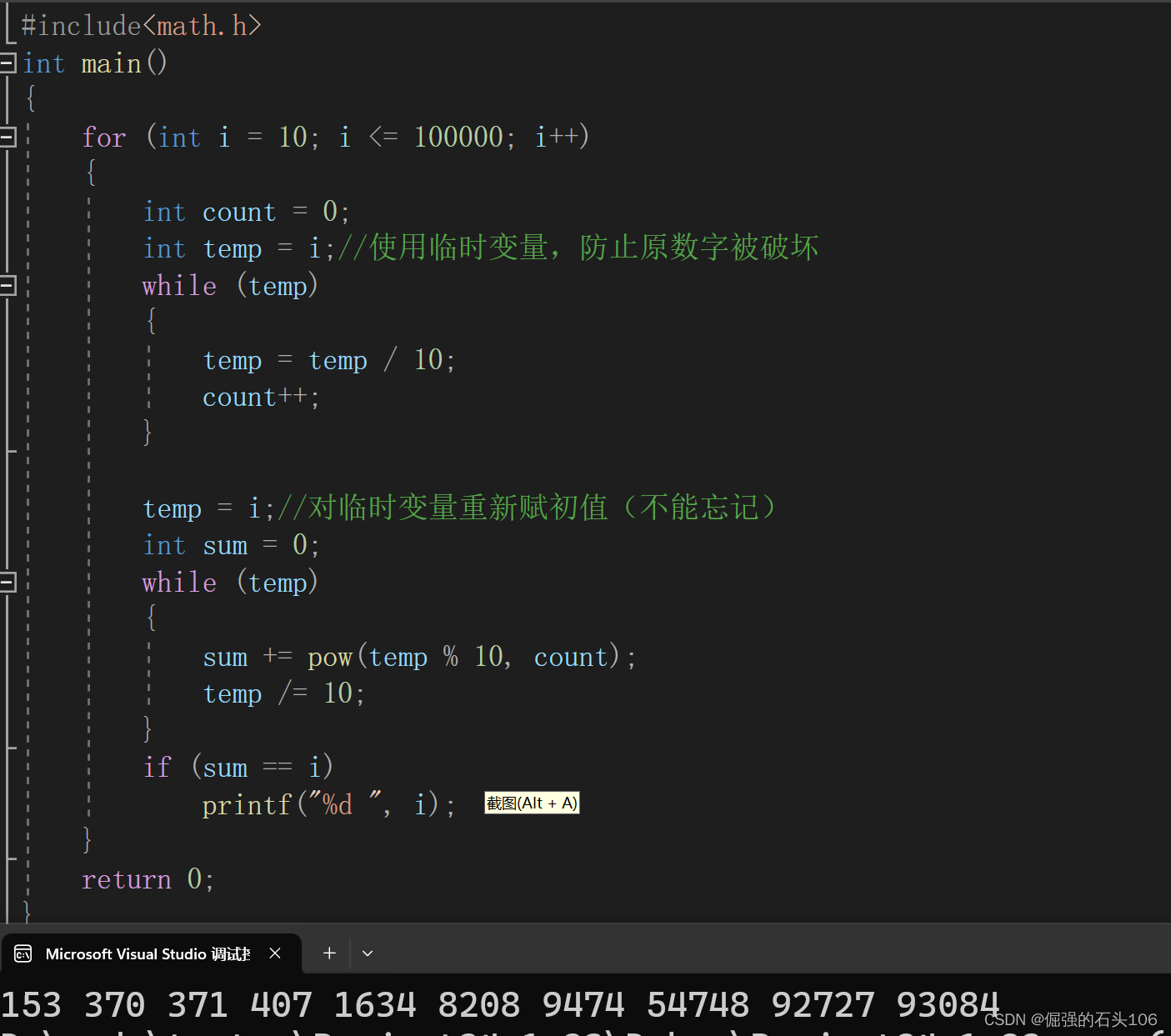
【C语言刷题系列】水仙花数的打印及进阶
1.水仙花数问题 水仙花数(Narcissistic number)也被称为超完全数字不变数(pluperfect digital invariant, PPDI)、自恋数、自幂数、阿姆斯壮数或阿姆斯特朗数(Armstrong number) 水仙花数是指一个 3 位数&a…...
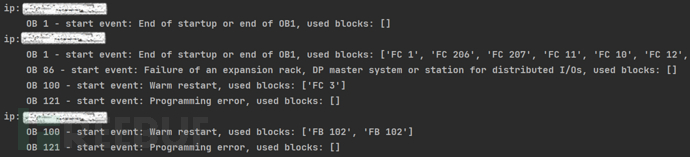
ICSpector:一款功能强大的微软开源工业PLC安全取证框架
关于ICSpector ICSpector是一款功能强大的开源工业PLC安全取证框架,该工具由微软的研究人员负责开发和维护,可以帮助广大研究人员轻松分析工业PLC元数据和项目文件。 ICSpector提供了方便的方式来扫描PLC并识别ICS环境中的可疑痕迹,可以用于…...

HCIA——29HTTP、万维网、HTML、PPP、ICMP;万维网的工作过程;HTTP 的特点HTTP 的报文结构的选择、解答
学习目标: 计算机网络 1.掌握计算机网络的基本概念、基本原理和基本方法。 2.掌握计算机网络的体系结构和典型网络协议,了解典型网络设备的组成和特点,理解典型网络设备的工作原理。 3.能够运用计算机网络的基本概念、基本原理和基本方法进行…...

面试经典题---3.无重复字符的最长子串
3.无重复字符的最长子串 我的解法: 滑动窗口: 维护一个[left, right)的滑动窗口,其中[left, right - 1]都是不重复子串;每轮while循环都计算一个滑动窗口的无重复子串长度len,每轮也让right后移一步; 内部…...

使用Robot Framework实现多平台自动化测试
基于Robot Framework、Jenkins、Appium、Selenium、Requests、AutoIt等开源框架和技术,成功打造了通用自动化测试持续集成管理平台(以下简称“平台”),显著提高了测试质量和测试用例的执行效率。 01、设计目标 平台通用且支持不…...
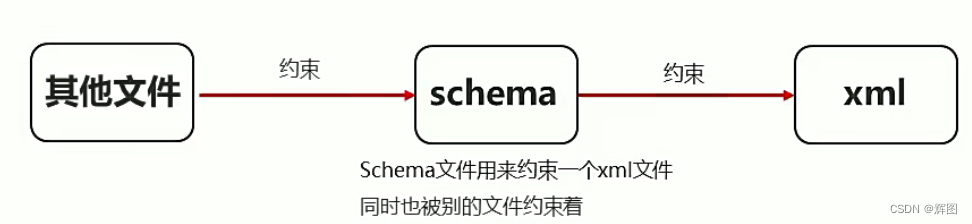
Java基础进阶02-xml
目录 一、XML(可拓展标记语言) 1.学习网站: 2.作用 3.XML标签 4.XML语法 5.解析XML (1)常见解析思想DOM 6.常见的解析工具 7.DOM4j的使用 8.文档约束 (1)概述 (2…...

《开始使用PyQT》 第01章 PyQT入门 03 用户界面介绍
03 用户界面介绍 《开始使用PyQT》 第01章 PyQT入门 03 用户界面介绍 The user interface (UI) has become a key part of our everyday lives, becoming the intermediary between us and our ever-growing number of machines. A UI is designed to facilitate in human-co…...

HTML-列表
列表 abbr: li : list item ol : orderd list ul : unordered list dl : definition list dt : definition title dd : definition description 1.有序列表(order list) 概念:有顺序或侧重顺序的列表 <h2>要把大象放冰箱总共分几步</h2> &…...
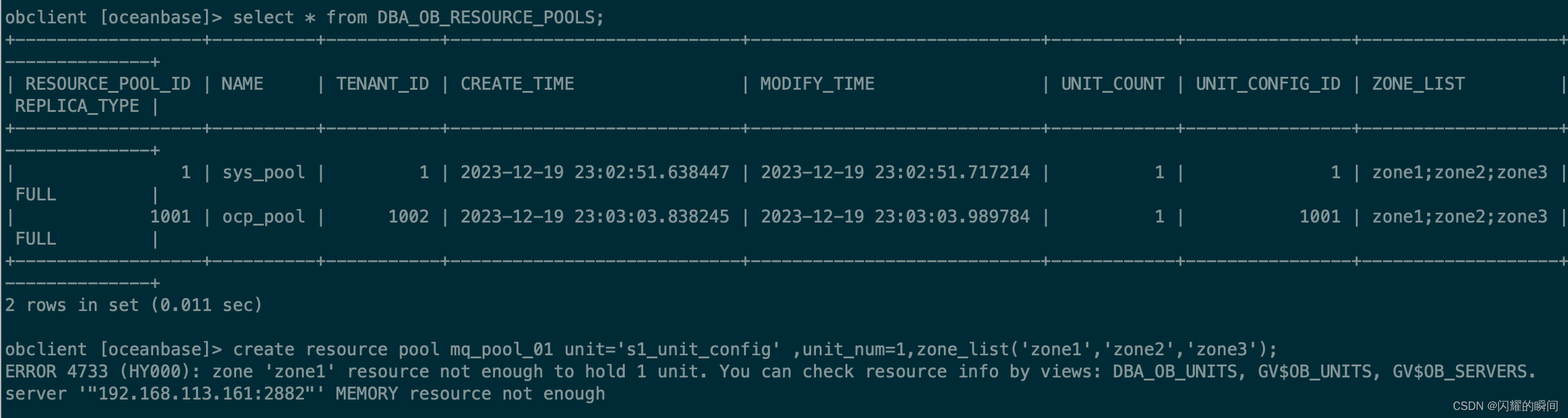
OceanBase创建租户
租户是集群之上的递进概念,OceanBase 数据库采用了多租户架构。 集群偏部署层面的物理概念,是 Zone 和节点的集合,租户则偏向于资源层面的逻辑概念,是在物理节点上划分的资源单元,可以指定其资源规格,包括…...
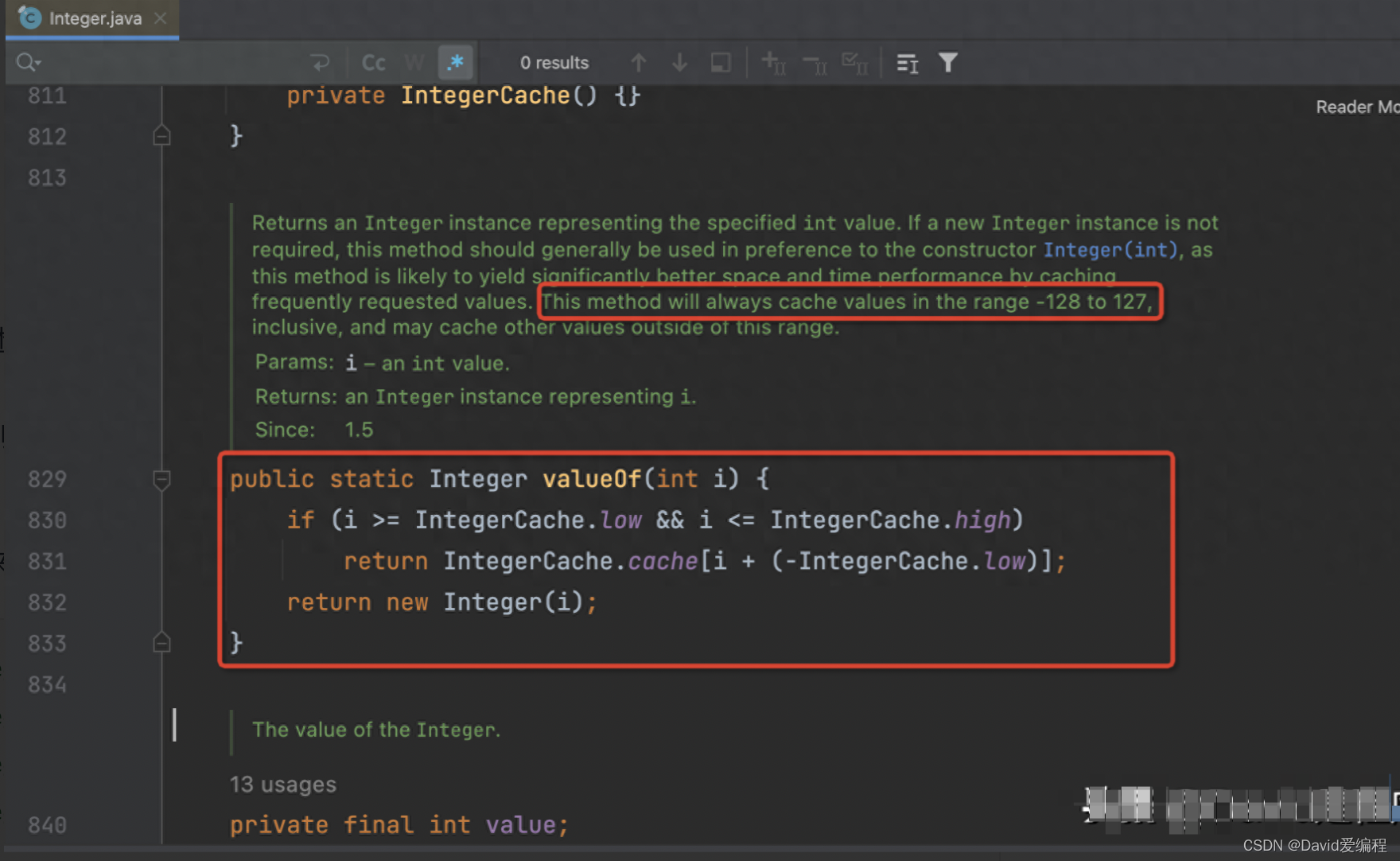
Java中Integer(127)==Integer(127)为True,Integer(128)==Integer(128)却为False,这是为什么?
文章目录 1.前言2. 源码解析3.总结 1.前言 相信大家职业生涯中或多或少的碰到过Java比较变态的笔试题,下面这道题目大家应该不陌生: Integer i 127; Integer j 127;Integer m 128; Integer n 128;System.out.println(i j); // 输出为 true System.o…...
【Unity】粒子贴图异常白边问题
从PS制作的黑底,白光的贴图。放入Unity粒子中,拉远看会有很严重的白边,像马赛克一样。 材质使用:Mobile/Particles/Additive 经测试只使用一张黑色的图片,也会有白边。 解决方案: 关闭黑色底…...

bxCAN接收处理
接收处理 为了接收 CAN 消息,提供了构成 FIFO(First Input First Output) 的三个邮箱。为了节约 CPU 负载,简化软件并保证数据一致性,FIFO 完全由硬件进行管理。应用程序通过 FIFO 输出邮箱访问 FIFO 中所存储的消息。 有效消息 当消息依据…...
前端面试题-(浏览器内核,CSS选择器优先级,盒子模型,CSS硬件加速,CSS扩展)
前端面试题-(浏览器内核,CSS选择器优先级,盒子模型,CSS硬件加速,CSS扩展) 常见的浏览器内核CSS选择器优先级盒子模型CSS硬件加速CSS扩展 常见的浏览器内核 内核描述Trident(IE内核)主要用在window系统中的IE浏览器中&…...

WEB前端标签的使用
图片标签 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title></head><body><!-- img标签就是用来将图片显示在页面上的标签 --><img src"图片路径"><!-- 可用路径&#…...

739. 每日温度
提示给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。 示例 1: 输入: tempe…...
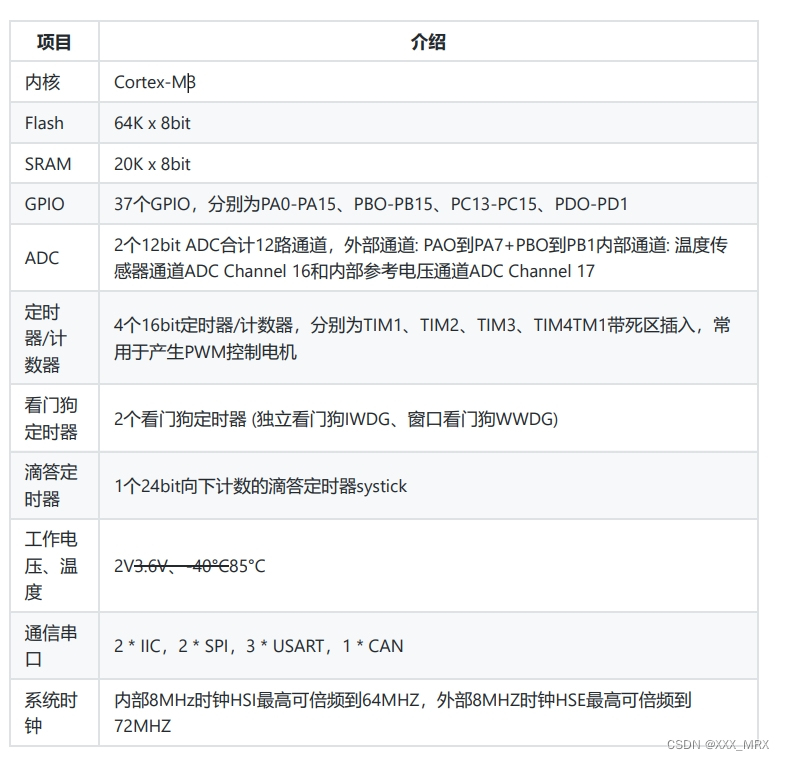
stm32F103C8T6简介及标准库和HAL库的区别
什么是单片机 单片机是一种集成电路芯片,把具有数据处理能力的中央处理器CPU、随机存储器RAM、只读存储器ROM、多种I/O和中断系统、定时器/计数器等功能(可能还包括显示驱动电路、脉宽调制电路、模拟多路转换电路、A\D转换器等电路)集成到一…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
