【代码随想录14】104.二叉树的最大深度 111.二叉树的最小深度 222.完全二叉树的节点个数

目录
- 104.二叉树的最大深度
- 题目描述
- 参考代码
- 111.二叉树的最小深度
- 题目描述
- 参考代码
- 222.完全二叉树的节点个数
- 题目描述
- 参考代码
104.二叉树的最大深度
题目描述
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
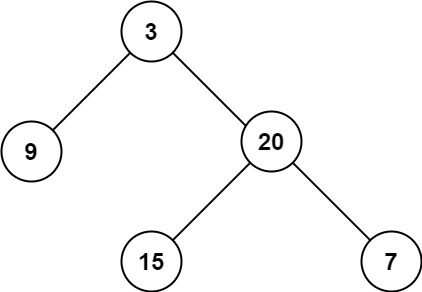
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
- 树中节点的数量在
[0, 104]区间内。 -100 <= Node.val <= 100
参考代码
class solution {/*** 递归法*/public int maxDepth(TreeNode root) {if (root == null) {return 0;}int leftDepth = maxDepth(root.left);int rightDepth = maxDepth(root.right);return Math.max(leftDepth, rightDepth) + 1;}
}
111.二叉树的最小深度
题目描述
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
**说明:**叶子节点是指没有子节点的节点。
示例 1:
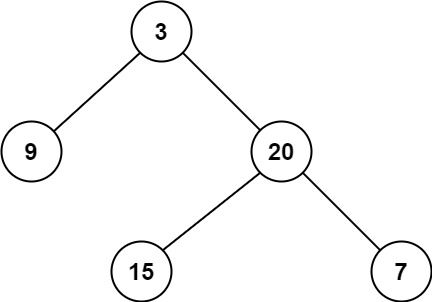
输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
提示:
- 树中节点数的范围在
[0, 105]内 -1000 <= Node.val <= 1000
参考代码
class Solution {/*** 递归法,相比求MaxDepth要复杂点* 因为最小深度是从根节点到最近**叶子节点**的最短路径上的节点数量*/public int minDepth(TreeNode root) {if (root == null) {return 0;}int leftDepth = minDepth(root.left);int rightDepth = minDepth(root.right);if (root.left == null) {return rightDepth + 1;}if (root.right == null) {return leftDepth + 1;}// 左右结点都不为nullreturn Math.min(leftDepth, rightDepth) + 1;}
}
222.完全二叉树的节点个数
题目描述
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:
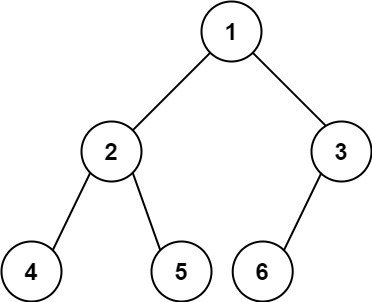
输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
提示:
- 树中节点的数目范围是
[0, 5 * 104] 0 <= Node.val <= 5 * 104- 题目数据保证输入的树是 完全二叉树
参考代码
class Solution {// 通用递归解法public int countNodes(TreeNode root) {if(root == null) {return 0;}return countNodes(root.left) + countNodes(root.right) + 1;}
}
Node root) {
if(root == null) {
return 0;
}
return countNodes(root.left) + countNodes(root.right) + 1;
}
}
相关文章:

【代码随想录14】104.二叉树的最大深度 111.二叉树的最小深度 222.完全二叉树的节点个数
目录 104.二叉树的最大深度题目描述参考代码 111.二叉树的最小深度题目描述参考代码 222.完全二叉树的节点个数题目描述参考代码 104.二叉树的最大深度 题目描述 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径…...
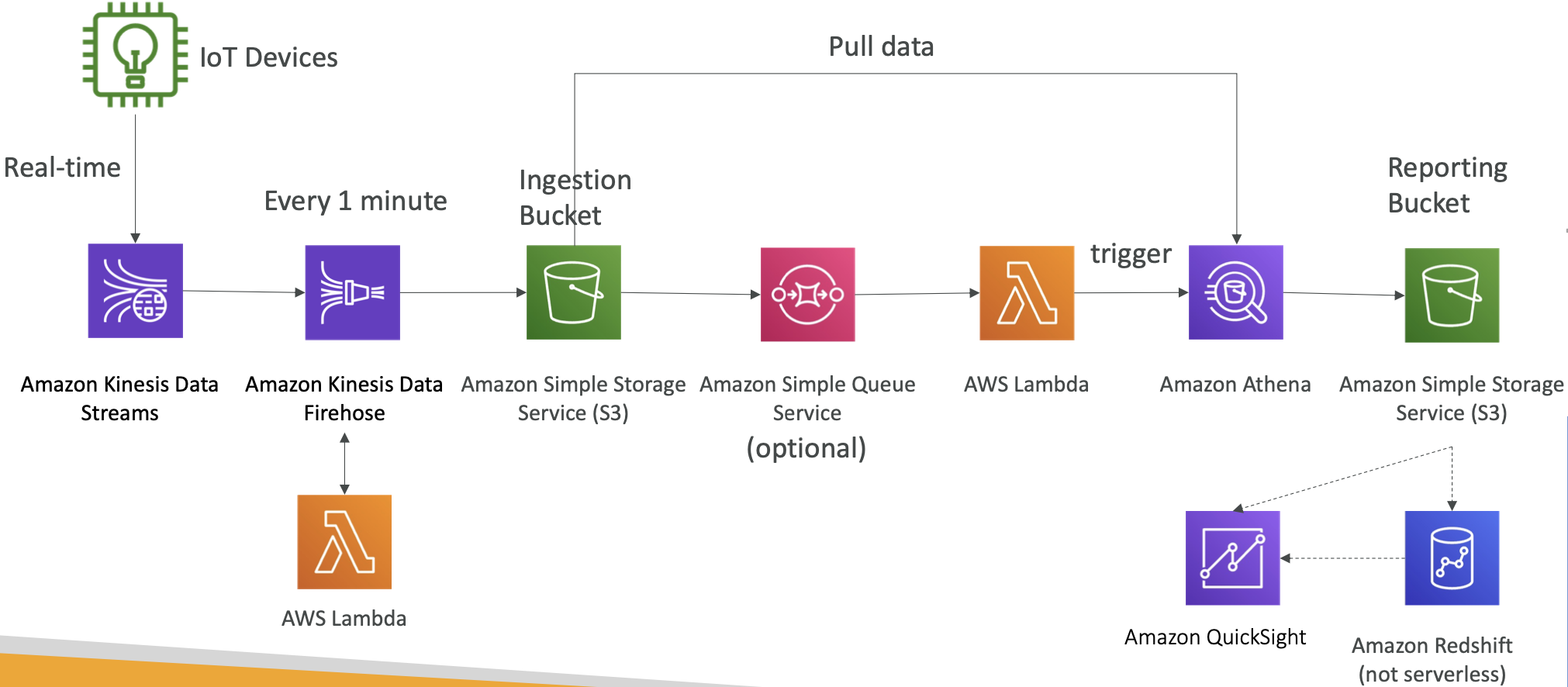
AWS 专题学习 P10 (Databases、 Data Analytics)
文章目录 专题总览1. Databases1.1 选择合适的数据库1.2 数据库类型1.3 AWS 数据库服务概述Amazon RDSAmazon AuroraAmazon ElastiCacheAmazon DynamoDBAmazon S3DocumentDBAmazon NeptuneAmazon Keyspaces (for Apache Cassandra)Amazon QLDBAmazon Timestream 2. Data & …...
一键拥有你的GPT4
这几天我一直在帮朋友升级ChatGPT,现在已经可以闭眼操作了哈哈😝。我原本以为大家都已经用上GPT4,享受着它带来的巨大帮助时,但结果还挺让我吃惊的,还是有很多人仍苦于如何进行升级。所以就想着写篇教程来教会大家如何…...
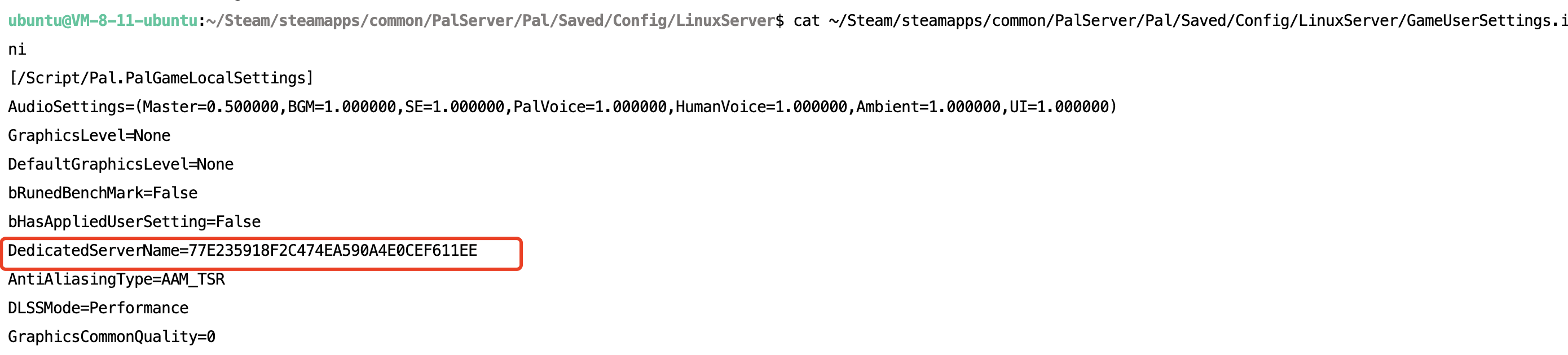
幻兽帕鲁服务器数据备份
搭建幻兽帕鲁个人服务器,最近不少用户碰到内存不足、游戏坏档之类的问题。做好定时备份,才能轻松快速恢复游戏进度 这里讲一下如何定时将服务器数据备份到腾讯云轻量对象存储服务,以及如何在有需要的时候进行数据恢复。服务器中间的数据迁移…...

【Digester解析XML文件的三种方式】
Digester解析XML文件的三种方式 1. Digester解析XML文件的三种方式1.1 作用及依赖jar包 2. 重点和难点3. XML文件4. 通过不同的方式解析这个xml文件4.1 通过java编码方式解析(javabean存储)4.2 通过java编码方式解析(list和map存储࿰…...
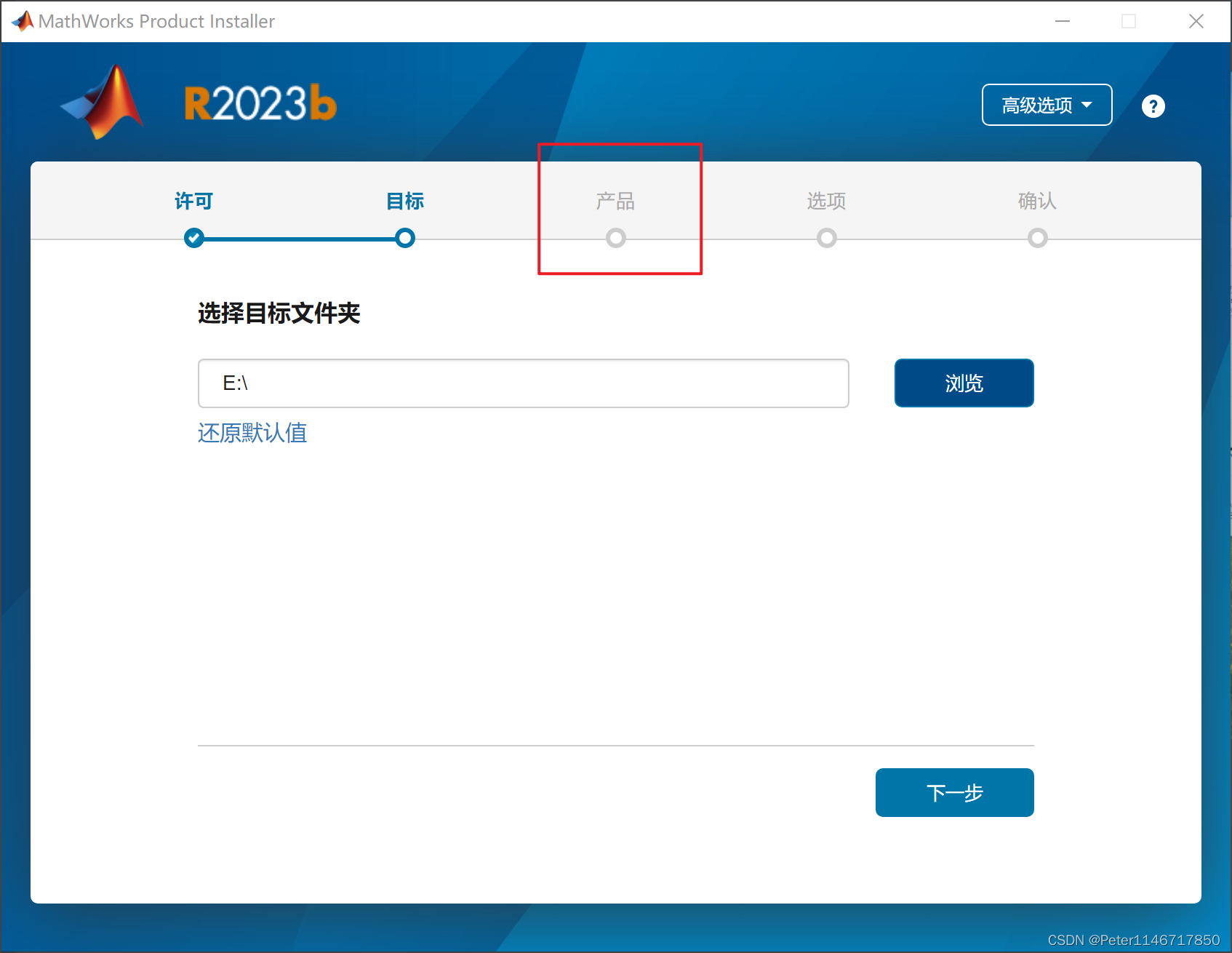
MATLAB curve fitting toolbox没有怎么办?
版本:MATLAB R2023b 如果在安装MATLAB时仅仅选择了安装MATLAB,而并未选择其他选项,则在进入MATLAB后会发现顶部的APP栏中无法找到曲线拟合工具箱。 本人跟随MATLAB中的教程进行下载时,出现了如下报错: 最终解决方案&a…...

Linux之快速入门(CentOS 7)
文章目录 一、Linux目录结构二、常用命令2.1 切换用户2.2查看ip地址2.3 cd2.4 目录查看2.5 查看文件内容2.6 创建目录及文件2.7 复制和移动2.8 其他2.9 tar3.0 which3.1 whereis3.2 find(这个命令尽量在少量用户使用此软件时运行,因为此命令是真的读磁盘…...

Spring框架中的设计模式
🎉欢迎来到Spring专栏:Spring框架中的设计模式 📜其他专栏:java面试 数据结构 源码解读 故障分析 🎬作者简介:大家好,我是小徐🥇☁️博客首页:CSDN主页小徐的博客&#x…...

Java数据结构与算法:邻接矩阵和邻接表
Java数据结构与算法:邻接矩阵和邻接表 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 什么是邻接矩阵和邻接表? 在图的表示中,…...

【温故而知新】JavaScript类、类继承、静态方法
文章目录 前言一、类二、类继承三、静态方法四、热门文章 前言 JavaScript是一种广泛使用的编程语言,主要用于Web开发。它是一种脚本语言,这意味着它不需要像编译语言那样预先编译,而是在运行时解释和执行。JavaScript可以直接在浏览器中运行…...

小黑艰难的前端啃bug之路:内联元素之间的间隙问题
今天开始学习前端项目,遇到了一个Bug调了好久,即使margin为0,但还是有空格。 小黑整理,用四种方法解决了空白问题 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></tit…...

Ubuntu 申请 SSL证书并搭建邮件服务器
文章目录 Log 一、域名连接到泰坦(Titan)电子邮件二、NameSilo Hosting 避坑三、Ubuntu 搭建邮件服务器1. 环境准备2. 域名配置3. 配置 Postfix 和 Dovecot① 安装 Nginx② 安装 Tomcat③ 申请 SSL 证书(Lets Encrypt)④ 配置 pos…...
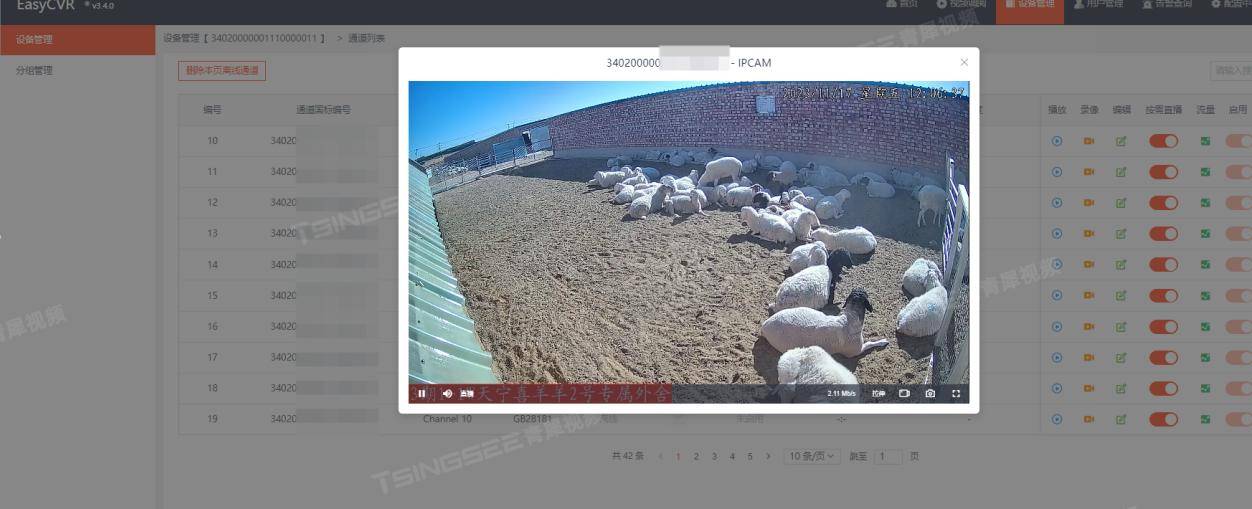
视频监控方案设计:EasyCVR视频智能监管系统方案技术特点与应用
随着科技的发展,视频监控平台在各个领域的应用越来越广泛。然而,当前的视频监控平台仍存在一些问题,如视频质量不高、监控范围有限、智能化程度不够等。这些问题不仅影响了监控效果,也制约了视频监控平台的发展。 为了解决这些问…...

pyspark.sql.types 中的类型有哪些
对 pyspark.sql.types 中的类型做个记录 1、首先正常使用的时候,我们需要引用他们: from pyspark.sql.types import MapType,StringType # 或者 from pyspark.sql.types import *PySpark SQL TYPES是PySpark模型中的一个类,用于定义PySpark数…...
开源CRM客户管理系统-FeelCRM
FeelCRM客户管理系统 开源项目介绍 FeelCRM客户管理系统,符合中小企业业务流程;支持线索管理、客户管理、商机管理、合同管理、审核管理等多个模块;希望能为广大中小企业以及开发者们提供一个更多的可能性;本版本是我公司跨语言…...

Linux创建新分区挂载后普通用户没有读写权限
Linux创建新分区挂载后普通用户没有读写权限 为了使用更大的空间,楼主按照 ubuntu 16.04 硬盘分区,挂载,硬盘分区方案 这个教程新建硬盘分区给普通用户挂载后,发现普通用户没有权限对挂载的文件夹进行读写。 导致无论是创建文…...

清越 peropure·AI 国内版ChatGP新功能介绍
当OpenAI发布ChatGPT的时候,没有人会意识到,新一代人工智能浪潮将给人类社会带来一场眩晕式变革。其中以ChatGPT为代表的AIGC技术加速成为AI领域的热门发展方向,推动着AI时代的前行发展。面对技术浪潮,清越科技(PeroPure)立足多样化生活场景、精准把握用户实际需求,持续精确Fin…...

力扣1027. 最长等差数列
动态规划 思路: 可以参考力扣1218. 最长定差子序列目前不清楚公差,可以将序列最大最小值找到,公差的范围是 [-(max - min), (max - min)],按公差递增迭代遍历求出最长等差数列; class Solution { public:int longest…...
)
GraphicsMagick 的 OpenCL 开发记录(二十三)
文章目录 ImageMagick和GraphicsMagick函数及宏对照表 <2022-04-14 周四> ImageMagick和GraphicsMagick函数及宏对照表 在开发过程中收集了这两个项目中的一些相同或相似功能的函数或者宏定义,希望对大家有所帮助,如下: TypeImageMa…...
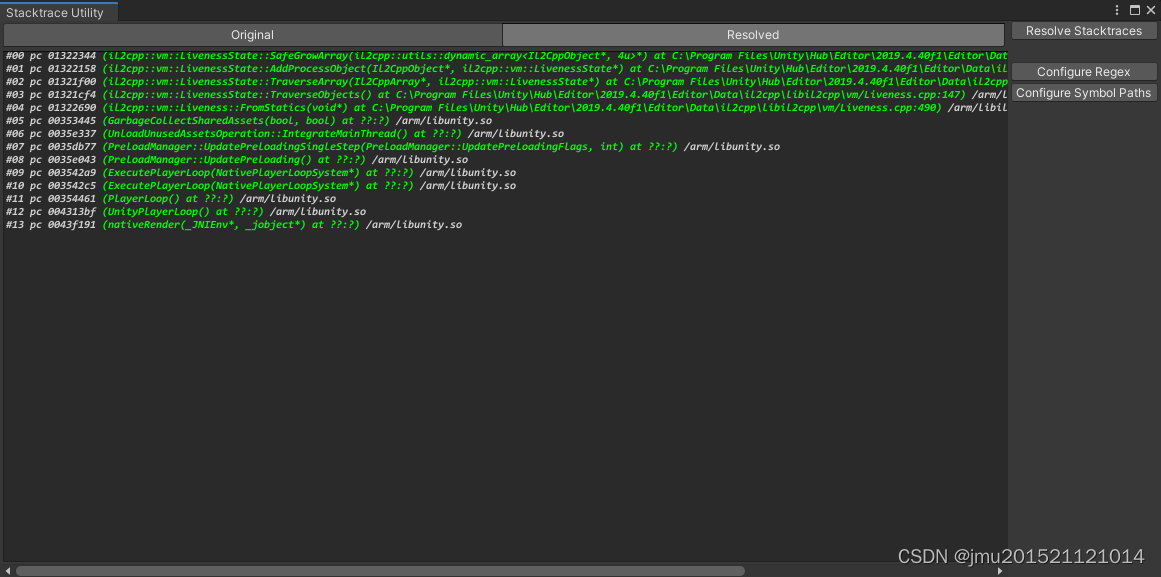
通过Android Logcat分析firebase崩溃
参考:UnityIL2CPP包Crash闪退利用Android Logcat还原符号表堆栈日志 - 简书 一、安装Android Logcat插件 1、新建空白unity工程,打开PackageManager窗口,菜单栏Window/PackageManager 2、PackageManager中安装Android Logcat日志工具 3、安…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
