第十四届蓝桥杯国赛 C++ B 组 C 题——班级活动(AC)
目录
- 1. 班级活动
- 1. 问题描述
- 2. 输入格式
- 3. 输出格式
- 4. 样例输入
- 5. 样例输出
- 6. 样例说明
- 7. 评测用例规模与约定
- 8. 原题链接
- 2. 解题思路
- 3. AC_Code
1. 班级活动
前置知识点:思维,分类讨论
1. 问题描述
小明的老师准备组织一次班级活动。班上一共有 n n n 名 ( n n n 为偶数) 同学,老师想把所有的同学进行分组,每两名同学一组。为了公平,老师给每名同学随机分配了一个 n n n 以内的正整数作为 id \text{id} id,第 i i i 名同学的 id \text{id} id 为 a i a_i ai。
老师希望通过更改若干名同学的 id \text{id} id 使得对于任意一名同学 i i i,有且仅有另一名同学 j j j 的 id \text{id} id 与其相同 ( a i = a j a_i = a_j ai=aj)。请问老师最少需要更改多少名同学的 id \text{id} id?
2. 输入格式
输入共 2 2 2 行。
第一行为一个正整数 n n n。
第二行为 n n n 个由空格隔开的整数 a 1 , a 2 , . . . , a n a_1, a_2, ..., a_n a1,a2,...,an。
3. 输出格式
输出共 1 1 1 行,一个整数。
4. 样例输入
4
1 2 2 3
5. 样例输出
1
6. 样例说明
仅需要把 a 1 a_1 a1 改为 3 3 3 或者把 a 3 a_3 a3 改为 1 1 1 即可。
7. 评测用例规模与约定
对于 20 % 20\% 20% 的数据,保证 n ≤ 1 0 3 n ≤ 10^3 n≤103。
对于 100 % 100\% 100% 的数据,保证 n ≤ 1 0 5 n ≤ 10^5 n≤105。
8. 原题链接
班级活动
2. 解题思路
首先明确一点,假设某个 id \text{id} id 的同学数量为 x ( x > 2 ) x(x>2) x(x>2),因为题目要求任意 id \text{id} id 只能有两名同学,所以一定会有 x − 2 x-2 x−2 名同学修改自己的 id \text{id} id。我们可以计算出每个 id \text{id} id 需要修改自身的同学数量之和,并将这个数量设为 b b b,即满足:
b = ∑ i = 1 n max ( 0 , a i − 2 ) b=\sum_{i=1}^{n}\max(0,a_i-2) b=i=1∑nmax(0,ai−2)
还有一个特殊群体我们不能忽略,就是编号 id \text{id} id 唯一的同学,我们设这群同学的数量为 a a a。他们特殊在有可能需要修改自身 id \text{id} id,也有可能不需要,我们需要进行分类讨论。
- 当 b ≥ a b \ge a b≥a 时:
在这种情况下, id \text{id} id 唯一的 a a a 名同学是不需要修改自身 id \text{id} id 的。我们可以从 b b b 名同学中选出 a a a 名同学修改自身 id \text{id} id 去与 id \text{id} id 唯一的同学对应,剩下的 b − a b-a b−a 名同学仍然是需要修改自身 id \text{id} id 的,所以答案即是 b b b。
假设有一个 id \text{id} id 集合 A = { 1 , 2 , 3 , 4 , 4 , 4 , 4 , 5 , 5 , 5 , 5 , 5 } A= \lbrace1,2,3,4,4,4,4,5,5,5,5,5\rbrace A={1,2,3,4,4,4,4,5,5,5,5,5},此时 id \text{id} id 唯一的集合为 { 1 , 2 , 3 } \lbrace1,2,3\rbrace {1,2,3},必须修改的 id \text{id} id 集合为 { 4 , 4 , 5 , 5 , 5 } \lbrace4,4,5,5,5\rbrace {4,4,5,5,5}。我们只需要让后一个集合的 id \text{id} id 分别修改为 { 1 , 2 , 3 , 6 , 6 } \lbrace 1,2,3,6,6\rbrace {1,2,3,6,6} 即可符合要求。
- 当 b < a b<a b<a 时:
在这种情况下,部分 id \text{id} id 唯一的 a a a 名同学是需要修改自身 id \text{id} id 的。同样假设有一个 id \text{id} id 集合 A = { 1 , 2 , 3 , 4 , 5 , 5 , 5 , 5 , 5 , 5 , 6 , 7 } A=\lbrace1,2,3,4,5,5,5,5,5,5,6,7\rbrace A={1,2,3,4,5,5,5,5,5,5,6,7},此时 id \text{id} id 唯一的集合为 { 1 , 2 , 3 , 4 , 6 , 7 } \lbrace1,2,3,4,6,7\rbrace {1,2,3,4,6,7},必须修改的 id \text{id} id 集合为 { 5 , 5 , 5 , 5 } \lbrace5,5,5,5\rbrace {5,5,5,5}。按照同样策略,我们让必须修改的 id \text{id} id 集合与 id \text{id} id 唯一的集合对应上,即将必须修改的 id \text{id} id 集合变为 { 1 , 2 , 3 , 4 } \lbrace1,2,3,4\rbrace {1,2,3,4}。
但此时仍然发现 id \text{id} id 唯一的集合剩余的两个 id \text{id} id 为 { 6 , 7 } \lbrace6,7\rbrace {6,7},我们需要让他们它们一致,所以需要修改其中一个。
假设剩余 4 4 4 个呢?那我们需要修改 2 2 2 个。
假设剩余 8 8 8 个呢?那我们需要修改 4 4 4 个。
显然结论就是需要修改剩余 id \text{id} id 个数的一半,即这种情况下答案是:
a − b 2 + b \dfrac{a-b}{2}+b 2a−b+b
小疑问:如果 a-b 为奇数怎么办?
结论: a − b a-b a−b 一定为偶数。我们可以假设数组已经存在 c c c 对匹配好的 id \text{id} id,根据我们对 a , b a,b a,b 的定义,显然符合式子 a + b + 2 × c = n a+b+2\times c=n a+b+2×c=n。题目告知我们 n n n 一定为偶数,且 2 × c 2 \times c 2×c 也一定为偶数,那么 a + b a+b a+b 也一定为偶数,即说明 a , b a,b a,b 奇偶性一定相同,得证 a − b a-b a−b 一定为偶数。
时间复杂度: O ( n ) O(n) O(n)。
3. AC_Code
- C++
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;int n;
int main()
{cin >> n;map<int, int> cnt;for (int i = 0; i < n; ++i){int x;cin >> x;cnt[x]++;}int a = 0, b = 0;for (auto [x, y] : cnt){if (y == 1){a++;}else if (y > 2){b += y - 2;}}if (b >= a){cout << b << '\n';}else{cout << (a - b) / 2 + b << '\n';}return 0;
}- Java
import java.util.*;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();Map<Integer, Integer> cnt = new HashMap<>();for (int i = 0; i < n; ++i) {int x = sc.nextInt();cnt.put(x, cnt.getOrDefault(x, 0) + 1);}int a = 0, b = 0;for (Map.Entry<Integer, Integer> entry : cnt.entrySet()) {int y = entry.getValue();if (y == 1) {a++;} else if (y > 2) {b += y - 2;}}if (b >= a) {System.out.println(b);} else {System.out.println((a - b) / 2 + b);}}
}
- Python
n = int(input())
line = list(map(int, input().split()))
cnt = {}
for i in range(n):x = line[i]if x in cnt:cnt[x] += 1else:cnt[x] = 1
a = 0
b = 0
for y in cnt.values():if y == 1:a += 1elif y > 2:b += y - 2
if b >= a:print(b)
else:print((a - b) // 2 + b)
相关文章:
)
第十四届蓝桥杯国赛 C++ B 组 C 题——班级活动(AC)
目录 1. 班级活动1. 问题描述2. 输入格式3. 输出格式4. 样例输入5. 样例输出6. 样例说明7. 评测用例规模与约定8. 原题链接 2. 解题思路3. AC_Code 1. 班级活动 前置知识点:思维,分类讨论 1. 问题描述 小明的老师准备组织一次班级活动。班上一共有 n…...

GraphQL的力量:简化复杂数据查询
1. GraphQL GraphQL 是一种由 Facebook 开发并于 2015 年公开发布的数据查询和操作语言,也是运行在服务端的运行时(runtime)用于处理 API 查询的一种规范。不同于传统的 REST API,GraphQL 允许客户端明确指定它们需要哪些数据&am…...
python环境安装sklearn及报错解决
安装 如刚开始安装,还未遇到问题请直接从重新安装库开始看,如果遇到报错,从问题开始看 问题 python安装sklearn报错 ,报错信息如下 File "<stdin>", line 1pip install scikit-learn^ SyntaxError: invalid s…...

log4j:WARN Please initialize the log4j system properly的解决办法
背景:很多次创建新项目log4j都出现以下2个警告: log4j:WARN No appenders could be found for logger (org.springframework.boot.ApplicationServletEnvironment).log4j:WARN Please initialize the log4j system properly 网上查询都是在说缺少以下jar…...

虹科分享丨汽车技术的未来:Netropy如何测试和确保汽车以太网的性能
来源:艾特保IT 虹科分享丨汽车技术的未来:Netropy如何测试和确保汽车以太网的性能 原文链接:https://mp.weixin.qq.com/s/G8wihrzqpJJOx5i0o63fkA 欢迎关注虹科,为您提供最新资讯! #汽车以太网 #车载网络 #Netropy …...

代码CE:reference to ‘XX‘ is ambiguous
代码CE:reference to ‘XX’ is ambiguous 今天提交代码的时候一直错误,CE,搞不明白明明在dev上成功,为什么提交失败。 现在懂了,因为定义的变量和C内部函数或变量重名了。修改之后即可AC。 int data[21][21]{0}; int maxsum[21…...
如果想将企业微信的组织架构同步到内部知识库咋搞?方法来也!
在现代企业的运营中,内部知识库不仅储存了公司的宝贵知识资产,还充当着员工信息共享和协作的核心平台。为了保障知识库的效能最大化,使其成为支持决策、创新和培训的强大工具,企业必须拥有一套周到的权限管理机制。对此࿰…...
【c语言】扫雷
前言: 扫雷是一款经典的单人益智游戏,它的目标是在一个方格矩阵中找出所有的地雷,而不触碰到任何一颗地雷。在计算机编程领域,扫雷也是一个非常受欢迎的项目,因为它涉及到许多重要的编程概念,如数组、循环…...

自然语言处理的崛起:从初步分析到深度理解
自然语言处理(NLP)是计算机科学、人工智能和语言学的交叉领域,旨在让计算机能够理解和生成人类语言。随着时间的推移,NLP 经历了一系列革命性的变化,从简单的规则和模式匹配到如今的深度学习模型,它们使计算…...

Git学习笔记:版本回滚
文章目录 回到过去:开启新时间线,时间分叉路口1. 回溯开发2. 临时恢复特性3. 实验性开发4. 分支维护和发布5. 调试历史问题类比推理: 方法:1. 临时查看旧版本2. 永久回滚到旧版本3. 创建新的分支指向旧版本 回到过去:开…...

OpenCV图像的基本操作
图像的基本操作(Python) 素材图 P1:die.jpg P2:cool.jpg V:rabbit.mp4, 下载地址 读取展示-图像 import cv2img_1 cv2.imread(./die.jpg) # default cv2.IMREAD_COLOR print("die.jpg shape(imre…...

小白水平理解面试经典题目LeetCode 594 Longest Harmonious Subsequence(最大和谐字符串)
594 最大和谐字符串 这道题属于字符串类型题目,解决的办法还是有很多的,暴力算法,二分法,双指针等等。 题目描述 和谐数组是指一个数组里元素的最大值和最小值之间的差别 正好是 1 。 现在,给你一个整数数组 nums …...
Vue-35、Vue中使用ref属性
1、ref属性 2、代码 <template><div id"app"> <!-- <img alt"Vue logo" src"./assets/logo.png">--><h1 v-text"msg" ref"title"></h1><button click"showDOM" ref&…...
网络通信(15)-C#TCP客户端掉线重连实例
本文上接前面的文章使用Socket在C#语言环境下完成TCP客户端的掉线重连实例。 掉线重连需要使用心跳包发送测试网络的状态,进而进入重连循环线程。 前面实例完成的功能: 客户端与服务器连接,实现实时刷新状态。 客户端接收服务器的数据。 客户端发送给服务器的数据。 客…...
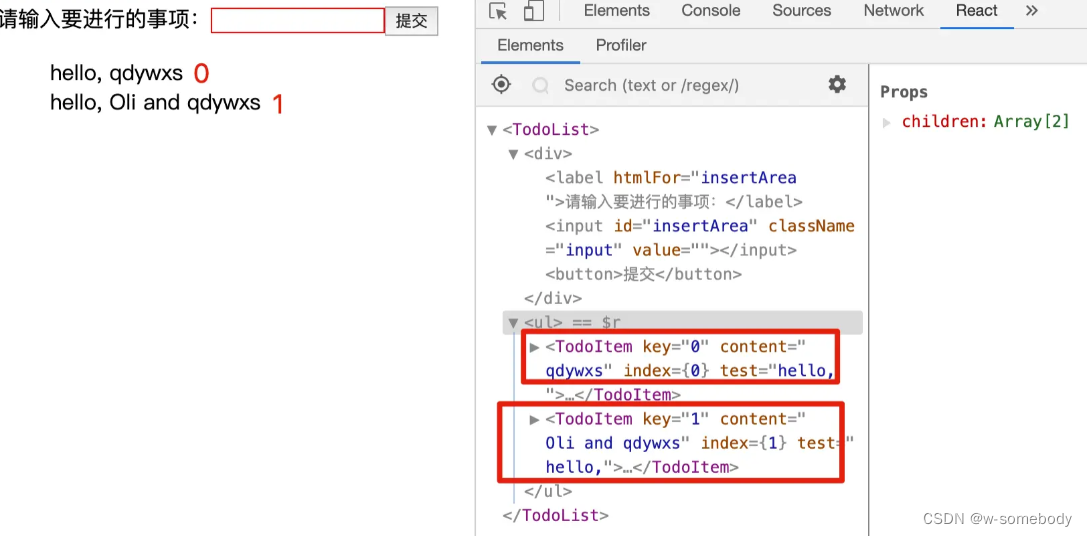
React进阶 - 14(说一说”虚拟DOM“中的”Diff算法“)
本章内容 目录 一、了解 Diff 算法二、key 值的重要性三、为什么不建议使用 index 做 key 值 上一节我们初步了解了 React中的”虚拟 DOM“ ,本节我们来说一说”虚拟DOM“中的”Diff算法“ 一、了解 Diff 算法 在上一篇中,我们有讲到:当 st…...

#GPU|LLM|AIGC#集成显卡与独立显卡|显卡在深度学习中的选择与LLM GPU推荐
区别 核心区别:显存,也被称作帧缓存。独立显卡拥有独立显存,而集成显卡通常是没有的,需要占用部分主内存来达到缓存的目的 集成显卡: 是集成在主板上的,与主处理器共享系统内存。 一般会在很多轻便薄型的…...

HCIP-IPV6实验
实验拓扑 实验需求 全网可达 实验思路 配置IP地址 配置路由协议-ospf 配置R2 配置IPV6 配置R2Tunnel 将所有地址引流到Tunnel0/0/0接口 ripng配置 汇总 实验步骤 配置IP地址 以R2为例 [Huawei]sys r2 [r2]int g0/0/0 [r2-GigabitEthernet0/0/0]ip address 12.1.1…...

如何训练和导出模型
介绍如何通过DI-engine使用DQN算法训练强化学习模型 一、什么是DQN算法 DQN算法,全称为Deep Q-Network算法,是一种结合了Q学习(一种价值基础的强化学习算法)和深度学习的算法。该算法是由DeepMind团队在2013年提出的,…...

Springboot注解@Aspect(一)之@Aspect 作用和Aop关系详解
目录 Aspect的使用 配置 作用 通知相关的注解 例子 结果: Aspect作用和Spring Aop关系 示例 标签表达式 Aspect的使用 配置 要启用 Spring AOP 和 Aspect 注解,需要在 Spring 配置中启用 AspectJ 自动代理,但是在 Spring Boot 中&a…...

自动化防DDoS脚本
简介 DDoS (分布式拒绝服务攻击)是一种恶意的网络攻击,旨在通过占用目标系统的资源,使其无法提供正常的服务。在DDoS攻击中,攻击者通常控制大量的被感染的计算机或其他网络设备,同时将它们协调起来向目标系…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
