2023王道考研数据结构笔记第四章串
第四章 串
4.1 串的定义
4.1.1 串的相关概念
-
串:即字符串(String)是由零个或多个字符组成的有限序列。一般记为S=‘a1a2…an’ (n>=0)
其中S是串名,单引号(注:有的地方用双引号,如Java、C,有的地方用单引号,如Python)括起来的字符序列是串的值;ai可以是字母、数字或其他字符。
-
串的长度:串中字符的个数 n,n = 0 时的串称为空串(用∅\emptyset∅表示)。
-
子串:串中任意个连续的字符组成的子序列。
-
主串:包含子串的串。
-
字符在主串中的位置:字符在串中的序号。(注意:位序从1开始而不是从0开始)
-
子串在主串中的位置:子串的第一个字符在主串中的位置 。
-
空串 vs 空格串 M=‘’ M是空串 N=’ ’ N是由三个空格字符组成的字符串,每个空格字符占1B
-
串 vs 线性表
① 串是一种特殊的线性表,数据元素之间呈线性关系
② 串的数据对象限定为字符集(如中文字符、英文字符、数字字符、标点字符等)
③ 串的基本操作,如增删改查等通常以字串为操作对象
4.1.2 串的基本操作
StrAssign(&T, chars):赋值操作。把串 T 赋值为 chars。StrCopy(&T, S):复制操作。由串 S 复制得到串 T。StrEmpty(S):判空操作。若 S 为空串,则返回 TRUE,否则返回 FALSE。StrLength(S):求串长。返回串 S 中元素的个数。ClearString(&S):清空操作。将 S 清为空串。DestroyString(&S):销毁串。将串 S 销毁(回收存储空间)。Concat(&T, S1, S2):串联接。用 T 返回由 S1 和 S2 联接而成的新串 。SubString(&Sub, S, pos, len):求子串。用 Sub 返回串 S 的第 pos 个字符起长度为 len 的子串。Index(S, T):定位操作。若主串 S 中存在与串 T 值相同的子串,则返回它在主串 S 中第一次出现的位置;否则函数值为 0。StrCompare(S, T):比较操作。若 S>T,则返回值>0;若 S=T,则返回值=0;若 S<T,则返回值<0。
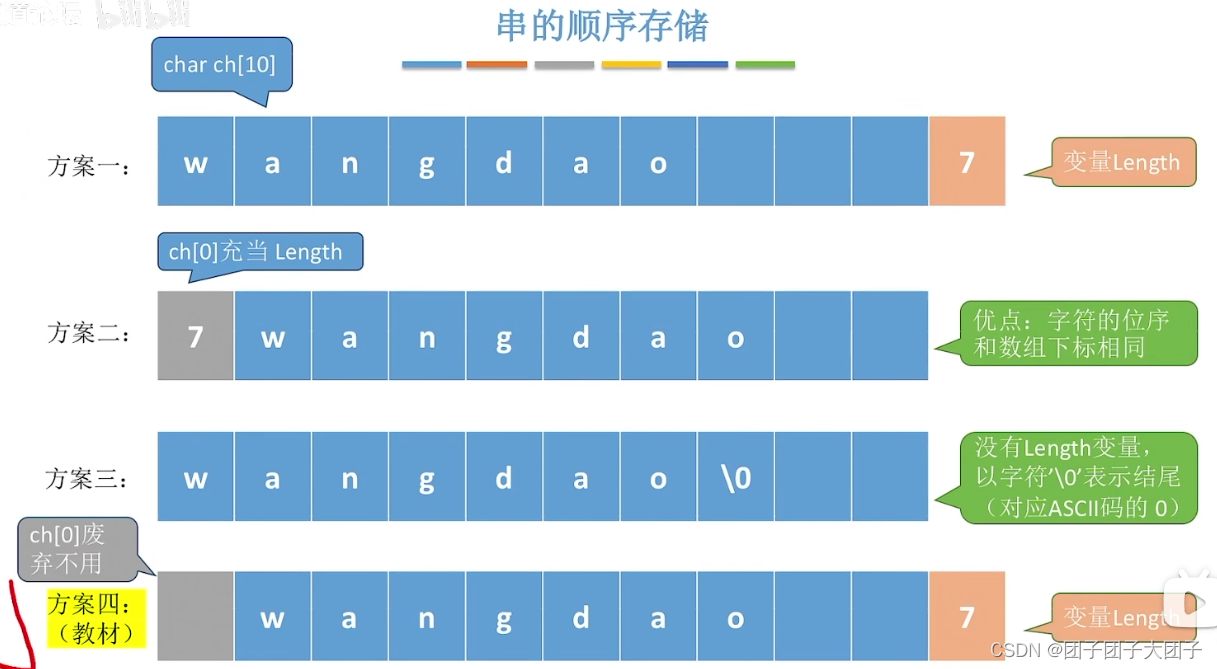
4.1.3 串的存储结构
1、静态数组实现(定长顺序存储)
#define MAXLEN 255 //预定义最大串长为255
typedef struct {char ch[MAXLEN]; // 每个分量存储一个字符int length; // 串的实际长度
} SString;
2、动态数组实现(堆分配存储)
typedef struct {char *ch; // 按串长分配存储区,ch指向串的基地址int length; // 串的长度
} HString;
HString S;
S.ch=(char *)malloc(MAXLEN*sizeof(char)); //用完需要手动free
S.length=0;
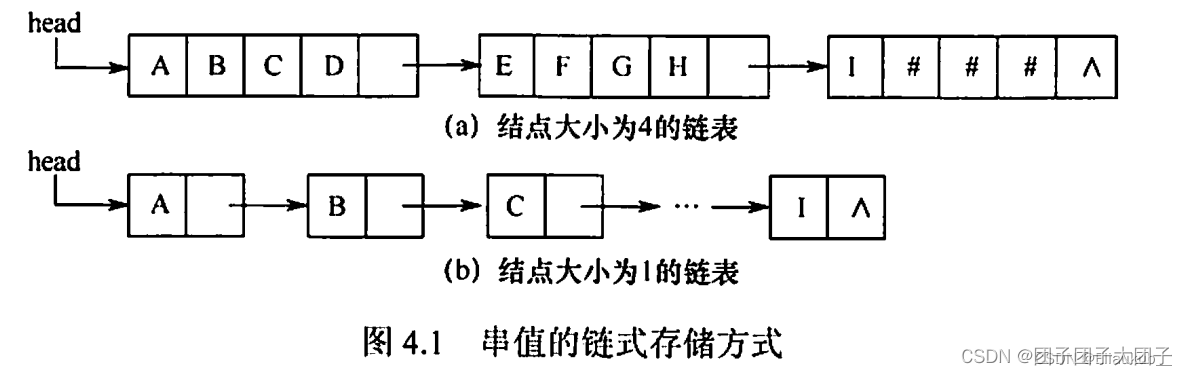
3、块链存储表示
默认情况下存储密度低,每个节点都只能存储一个字符
解决方法:一个结点存储多个字符
typedef struct StringNode{char ch; //存储密度低,每个字符1B,每个指针4Bstruct StringNode * next;
}StringNode,* String;typedef struct StringNode{char ch[4];struct StringNode *next;
}StringNode,* String; //存储密度提高
4.2 串的模式匹配
串的模式匹配:在主串中找到与模式串相同的子串,并返回其所在位置。
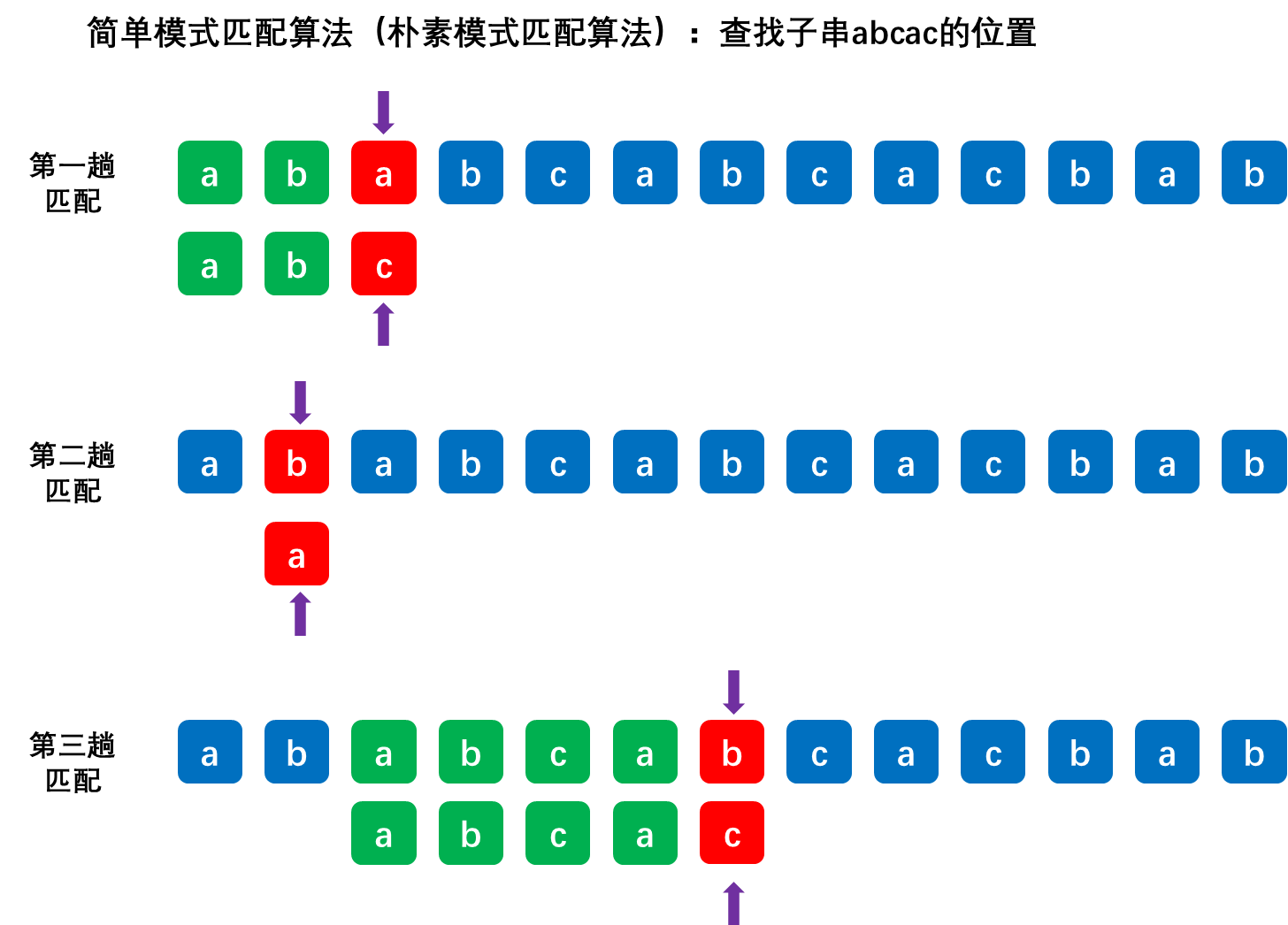
4.2.1 简单的模式匹配算法
思想:将主串中与模式串长度相同的字串拿出来,挨个与模式串对比
当子串与模式串某个对应字符不匹配时,就立即放弃当前子串,转而检索下一个子串
一个示例:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0yXK4hyr-1677904184313)(数据结构.assets/03d26afdd9a945d38b8e203366f3d634.png)]](https://img-blog.csdnimg.cn/53305c9899a94f97bab459adfaafe70b.png)
分析:
简单模式匹配算法的最坏时间复杂度是O(nm),即每个子串都要对比到最后一个字符,如下面这种情况:
- 主串:1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2
- 子串:1 1 1 1 1 1 1 1 2
其中,n和m分别是主串和模式串的长度。
最好的情况(对于每个子串都只需对比一次):
- 匹配成功:O(m)
- 匹配失败:O(n-m+1)=O(n-m)≈O(n)
4.2.2 KMP算法
朴素模式匹配算法的缺点:当某些子串与模式串能部分匹配时,主串的扫描指针i经常回溯,导致时间开销增加。
要了解子串的结构,首先需要了解以下几个概念:前缀、后缀和部分匹配值。
前缀:除了最后一个字符外,字符串的所有头部子串
后缀:除了第一个字符外,字符串的所有尾部子串
‘ab’的前缀是{a},后缀是{b},{a}∩{b}=∅,最长相等前后缀长度为0
'aba’的前缀为{a, ab},后缀为{a, ba}, {a, ab }∩{a, ba}={a),最长相等前后缀长度为1。
'abab '的前缀{a, ab,aba}∩后缀{b, ab, bab }={ab},最长相等前后缀长度为2。
'ababa '的前缀{a, ab,aba, abab }∩后缀{a , ba, aba, baba }={a, aba},公共元素有两个,最长相等前后缀长度为3。
故字符串’ababa’的部分匹配值为00123
接下来详解一下上面这个例子:
由上述方法求子串’abcac’的部分匹配值:
'ab’的前缀{a},后缀{b} {a}∩{b} = ∅
'abc’的前缀{a,ab}, 后缀{c, bc} {a,ab}∩{c, bc} = ∅
'abca’的前缀{a,ab,abc},后缀{a,ca,bca} {a,ab,abc}∩{a,ca,bca} = {a}
'abcac’的前缀{a,ab,abc,abca},后缀{c,ac,cac,bcac} {a,ab,abc}∩{c,ac,cac,bcac} = ∅
将其部分匹配值写成数组形式,就得到了部分匹配值(PM)的表:
| 编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| S | a | b | c | a | c |
| PM | 0 | 0 | 0 | 1 | 0 |
接下来可以使用PM表来进行字符串匹配,其过程如下
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Yp1IyodJ-1677904184313)(数据结构.assets/947517b937b04b7fa0c887b04eda7806.png)]](https://img-blog.csdnimg.cn/e4c6d1cbac34408fad27036008595aa8.png)
KMP算法的原理
当c与b不匹配时,已匹配’abca’的前缀a和后缀a为最长公共元素。已知前缀a与b、c均不同,与后缀a相同,故无须比较,直接将子串移动“已匹配的字符数–对应的部分匹配值”,用子串前缀后面的元素与主串匹配失败的元素开始比较即可。

对算法的改进
已知:右移位数=已匹配的字符数-对应的部分匹配值。写成:
Move=(j−1)−PM[j−1]Move=(j-1)-PM[j-1] Move=(j−1)−PM[j−1]
现在这种情况下,我们在匹配失败时,需要去查找它前一个元素的部分匹配值,这样使用起来有点不方便,故我们可以将PM表右移一位,这样哪个元素匹配失败,则直接看它自己的部分匹配值即可。
将上例的PM表右移一位,则得到了next数组
| 编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| S | a | b | c | a | c |
| next | -1 | 0 | 0 | 0 | 1 |
我们注意到:
1)第一个元素右移以后空缺的用-1来填充,因为若是第一个元素匹配失败,则需要将子串向右移动一位,而不需要计算子串移动的位数。
2)最后一个元素在右移的过程中溢出,因为原来的子串中,最后一个元素的部分匹配值是其下一个元素使用的,但显然已没有下一个元素,故可以舍去。
这样,上式就改写为:
Move=(j−1)−next[j]Move=(j-1)-next[j] Move=(j−1)−next[j]
就相当于将子串的比较指针回退到:
j=j−Move=j−((j−1)−next[j])=next[j]+1j=j-Move=j-((j-1)-next[j])=next[j]+1 j=j−Move=j−((j−1)−next[j])=next[j]+1
但为了让公式更加简洁,我们将next数组整体加1
next数组也可以写成:
| 编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| S | a | b | c | a | c |
| next | 0 | 1 | 1 | 1 | 2 |
最终子串指针变化公式为:
j=next[j]j=next[j] j=next[j]
在实际匹配过程中,子串在内存里是不会移动的,而是指针在变化,书中画图举例只是为了让问题描述得更加形象。next[j]的含义是:在子串的第j个字符与主串发生失配时,则跳到子串的next[j]位置重新与主串当前位置进行比较。
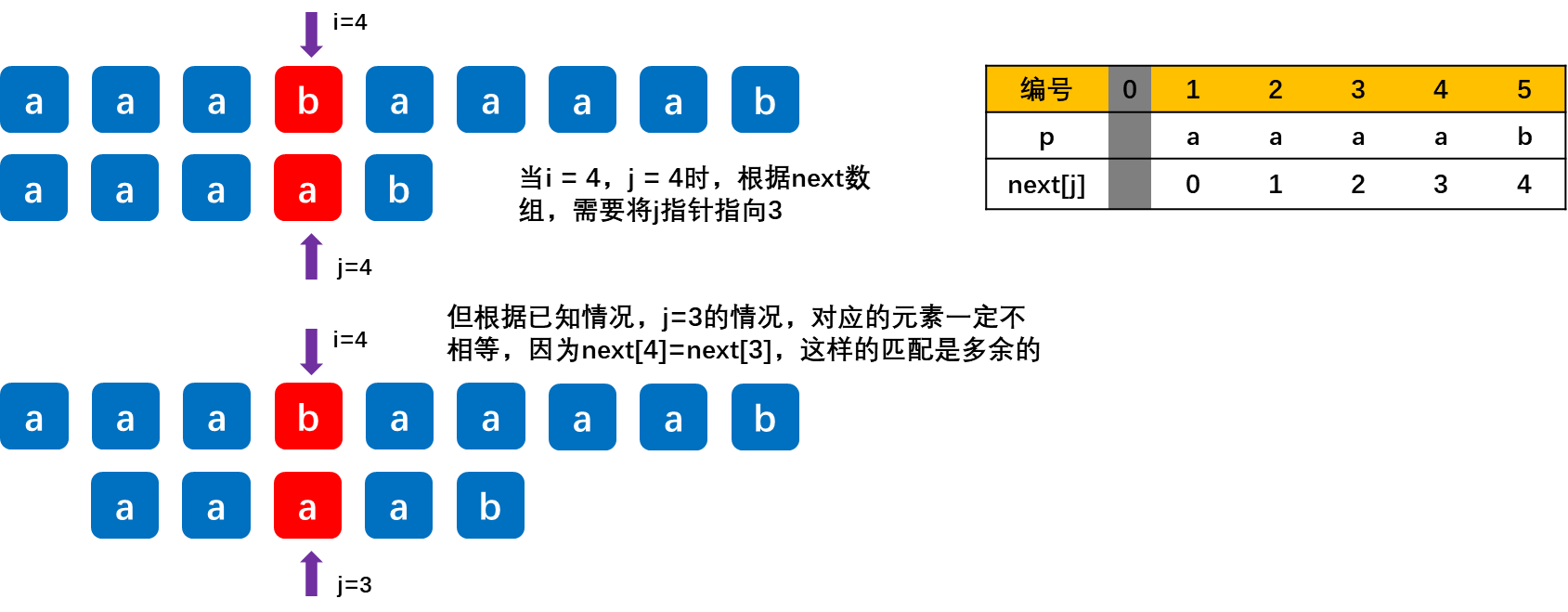
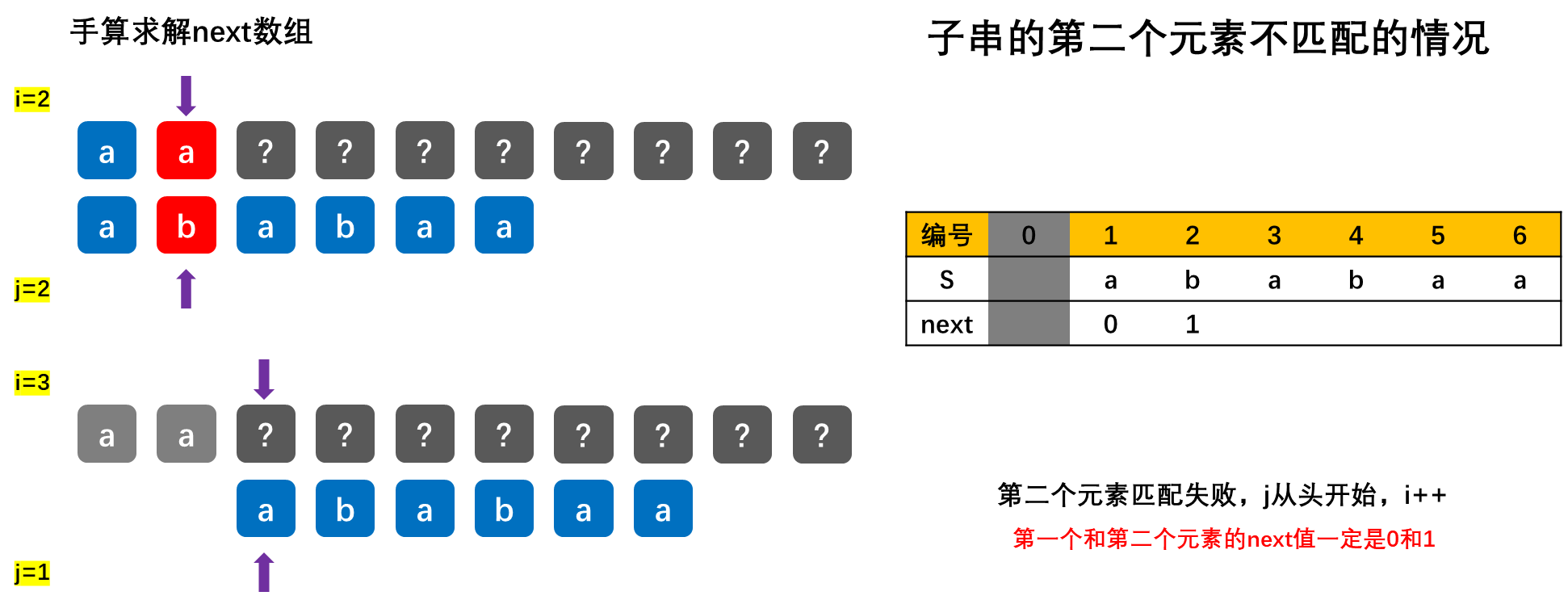
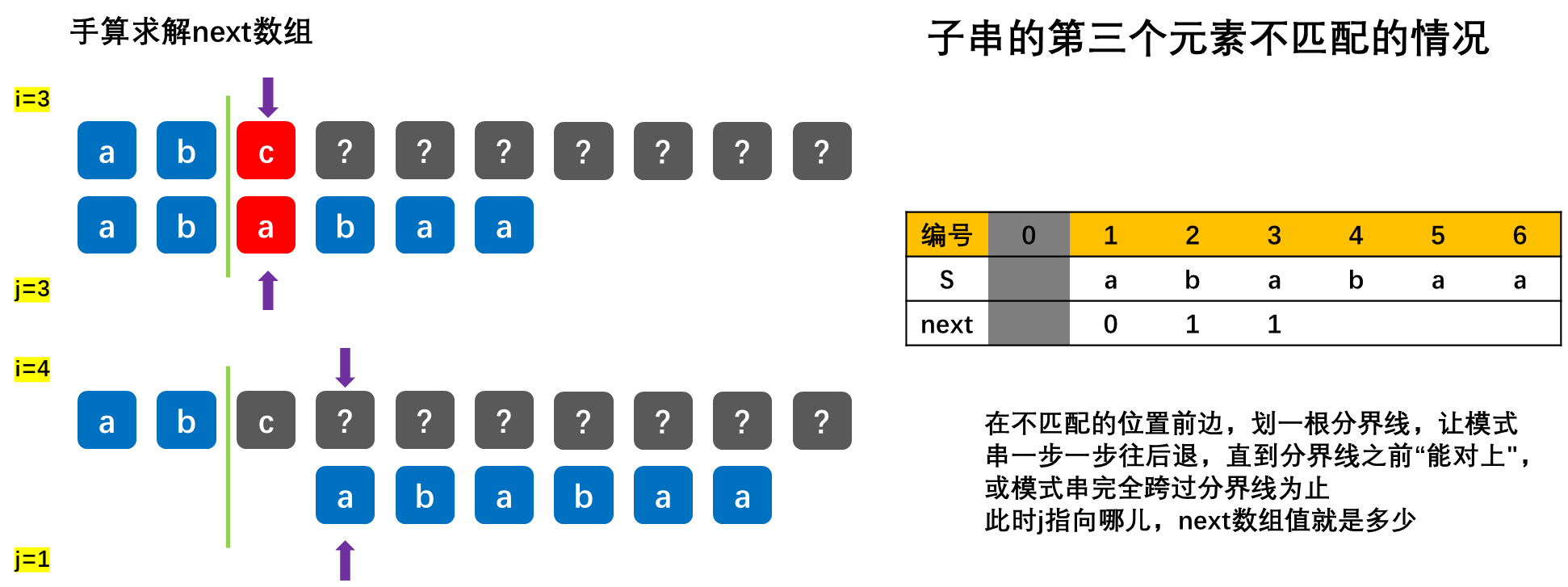
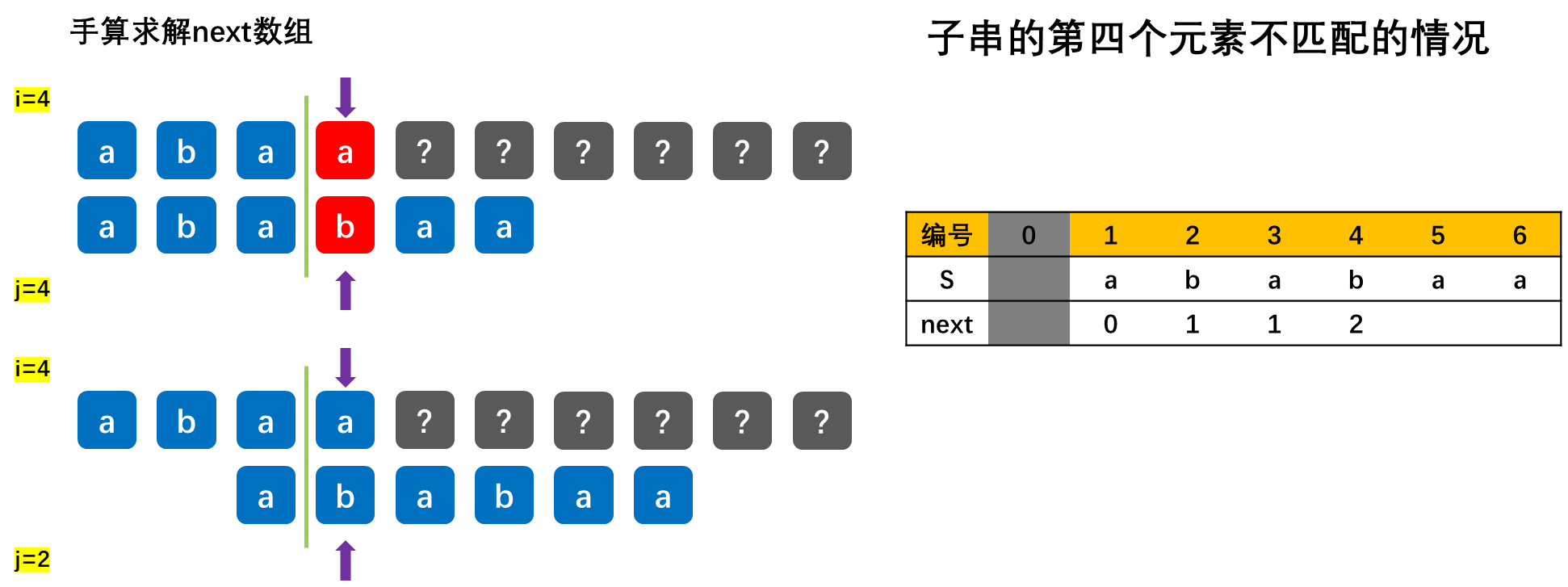
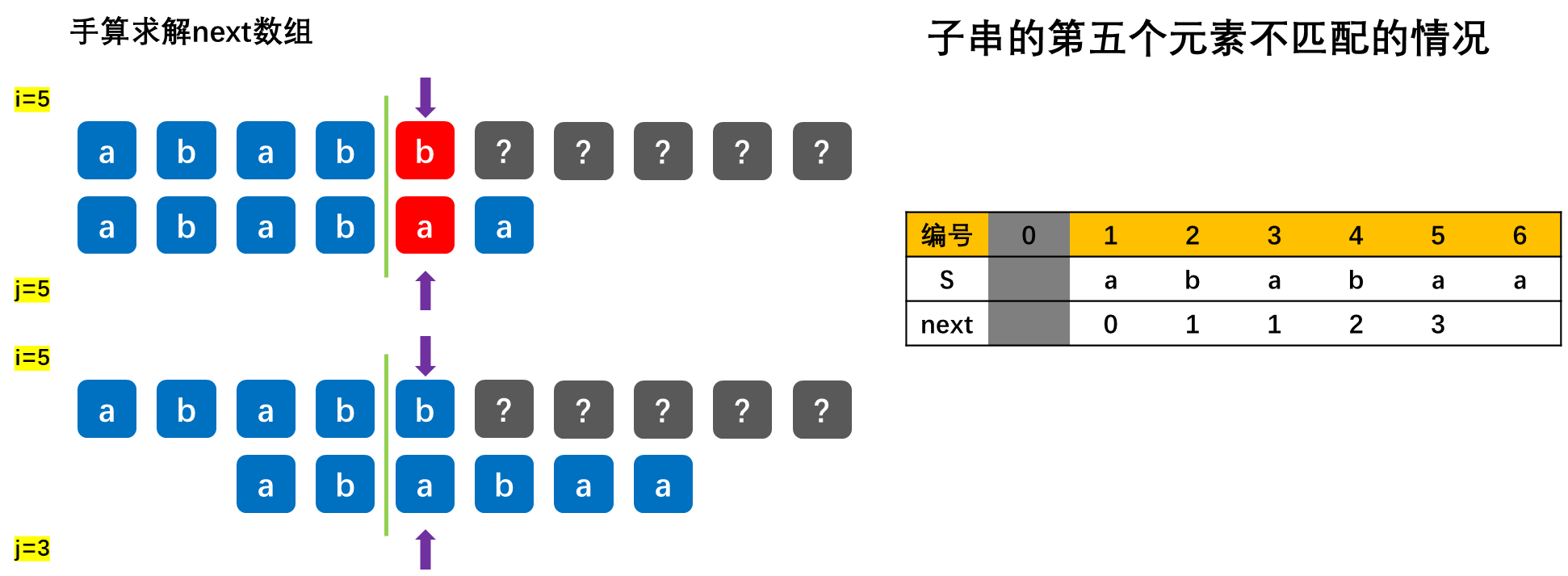
【重要】求next数组,根据如下示例来学习:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BbvJ23vz-1677904184314)(数据结构.assets/a90ce7d2ecbc4b13b4554658845e9167.png)]](https://img-blog.csdnimg.cn/02b0a7163fc944dba195d4f41f26c0d7.png)
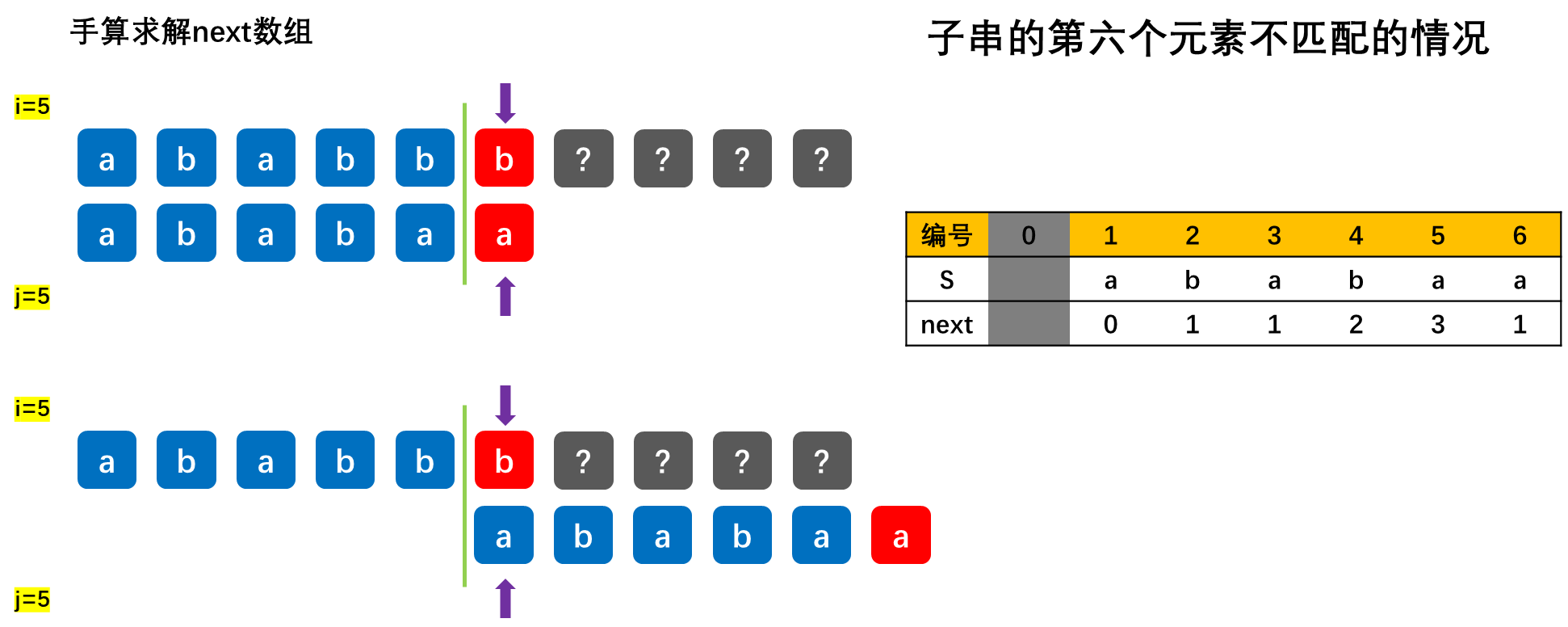
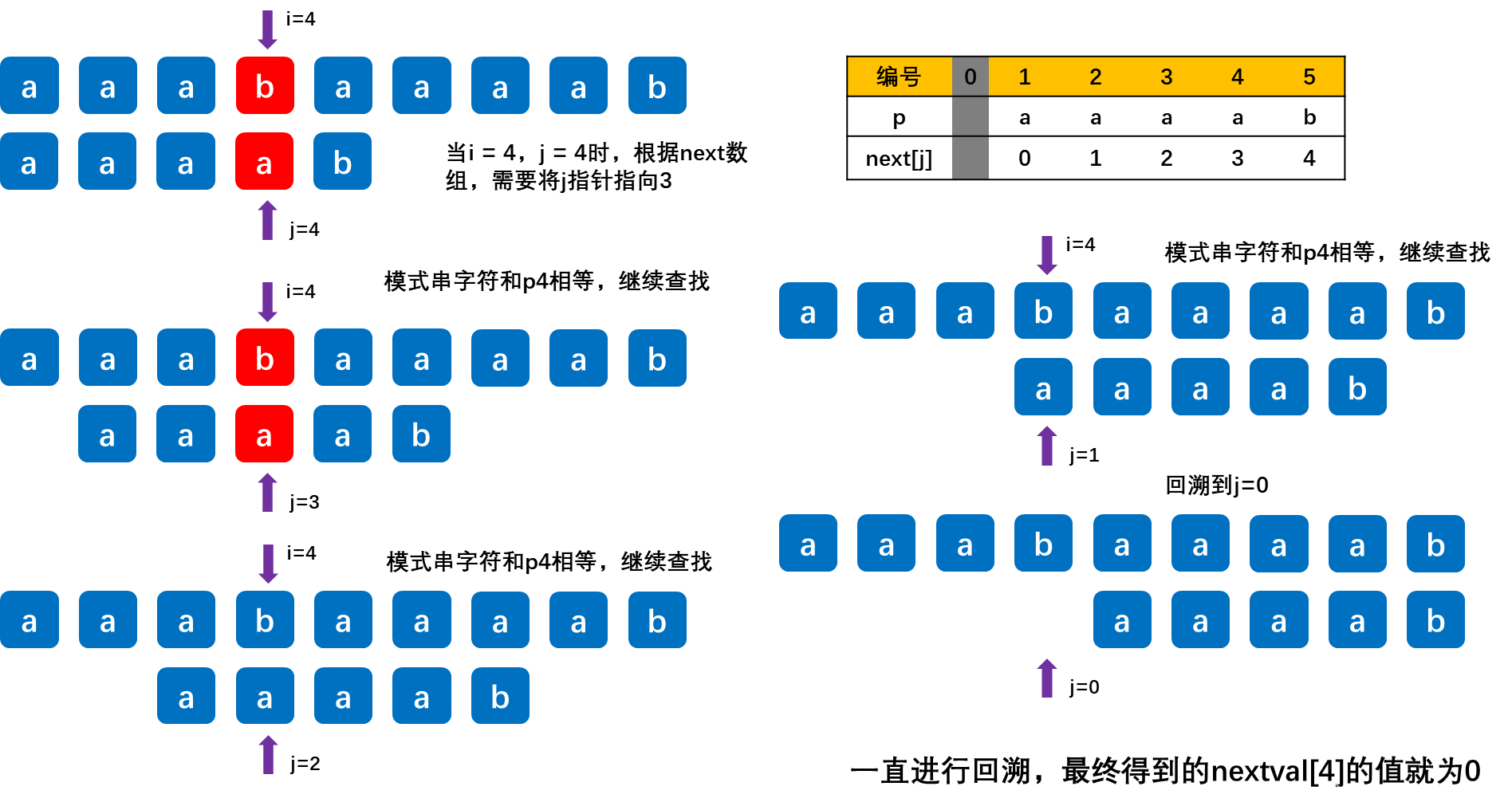
KMP算法的进一步优化
问题的产生:
所以引入了nextval数组,对KMP算法进行进一步优化。
故我们在模式串中,当前模式串p和对应的next数组p_next的模式串值相等时,继续查找对应p_next模式串的next数组对应的模式串,直到模式串对应的值不相等。
以下是匹配过程:
相关文章:

2023王道考研数据结构笔记第四章串
第四章 串 4.1 串的定义 4.1.1 串的相关概念 串:即字符串(String)是由零个或多个字符组成的有限序列。一般记为S‘a1a2…an’ (n>0) 其中S是串名,单引号(注:有的地方用双引号,如Java、C&am…...

【AI绘图学习笔记】深度学习相关数学原理总结(持续更新)
如题,这是一篇深度学习相关数学原理总结文,由于深度学习中涉及到较多的概率论知识(包括随机过程,信息论,概率与统计啥啥啥的),而笔者概率知识储备属实不行,因此特意开一章来总结(大部…...

CSGO服务器配置全贴纸插件方法教程
CSGO服务器配置全贴纸插件方法教程 关于插件的警告 一定要了解V社对于CSGO社区服务器的规定,全皮肤插件/全手套插件等,在设置了GSLT的情况下,是有可能被封禁GSLT账号的(所以慎用) 配置好服务器之后呢,想安…...
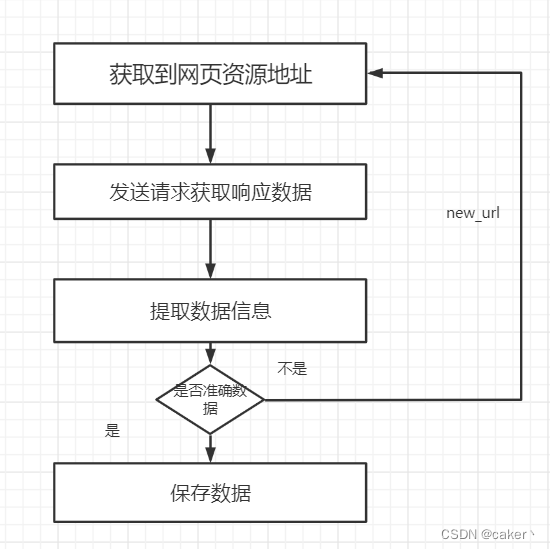
Python爬虫——使用socket模块进行图片下载
Python爬虫——使用socket模块进行图片下载什么是socket爬虫的工作流程socket爬取图片为什么能用socket能下载图片socket下载图片和request下载图片的区别使用socket下载一张图片使用socket下载多张图片方法1方法2什么是socket Socket 是一种通信机制,用于实现网络…...
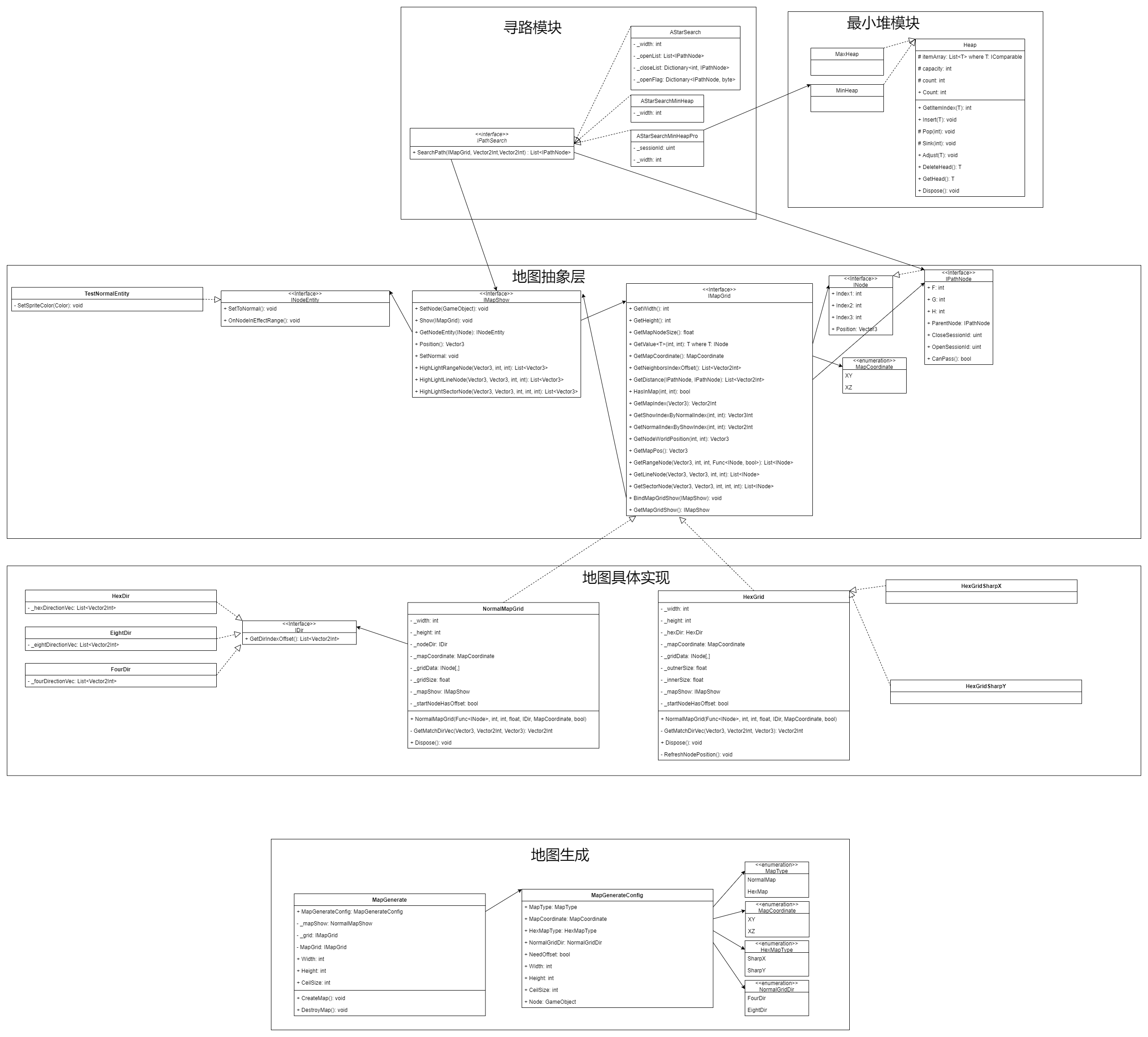
通用游戏地图解决方案设计解析
前言: 在软件开发过程中,我们都希望能设计出一个稳健的,可维护的系统,为了实现这个目的,人们总结出了很多相关的设计原则,比如SOLID原则, KISS原则等等。SOLID每个字母代表了一种设计原则&…...

java @Autowired @Resource @Inject 三个注解的区别
javax.annotation.Resourcejdk 内置的,JSR-250 中的注解。依赖注入通过 org.springframework.context.annotation.CommonAnnotationBeanPostProcessor 来处理。org.springframework.beans.factory.annotation.Autowired org.springframework.beans.factory.annotati…...

「媒体分流直播」媒体直播和传统直播的区别,以及媒体直播的特点
传媒如春雨,润物细无声,大家好直播毋庸置疑已经融入到了我们生活的方方面面,小到才艺,游戏,大到政策的发布,许多企业和机构也越来越重视直播,那么一场活动怎么最大化的进行传播,一是…...

数据是如何在计算机中存储的
我们普通人对于数据存储的认识恐怕大多数都是从自己使用的电脑来的。现在几乎人手一台电脑,而我们的电脑存储着各种各样的文件,比如视频文件、音频文件和Word文档等。这些文件从计算机术语的角度都可以称为数据。 如图1-1所示是Windows 10 “我的电脑”的截图。通过该截图我…...

Day907.分区表 -MySQL实战
分区表 Hi,我是阿昌,今天学习记录的是关于分区表的内容。 经常被问到这样一个问题: 分区表有什么问题,为什么公司规范不让使用分区表呢? 一、分区表是什么? 为了说明分区表的组织形式,先创建…...
C++概览:工具链、基础知识、进阶及总结
本篇写给C初学者,作为概览,文中仅包含各方面基础知识,无深入分析。 C基础概念简介 C编译过程示意图 关键词:源文件、预编译、编译、汇编、链接 C工具链总结 cmake项目工程文件是一种中介工程文件,可以转化成其他…...
目标检测中回归损失函数(L1Loss,L2Loss,Smooth L1Loss,IOU,GIOU,DIOU,CIOU,EIOU,αIOU ,SIOU)
文章目录L-norm Loss 系列L1 LossL2 LossSmooth L1 LossIOU系列IOU (2016)GIOU (2019)DIOU (2020)CIOU (2020)EIOU (2022)αIOU (2021)SIOU (2022…...
JOSN数据转换和解析
文章目录JOSN数据转换和解析内容回顾Map 集合转成 JSON 字符串List 集合转换成 JSON 字符串Ajax 异步和同步异步概念同步概念异步和同步区别异步请求案例同步请求时间格式化旧时间 api 格式化格式化和解析的工具类JSTL 时间格式化JSTL 使用JOSN数据转换和解析 内容回顾 ajax …...

浅析Linux内核中进程完全公平CFS调度
一、前序 目前Linux支持三种进程调度策略,分别是SCHED_FIFO 、 SCHED_RR和SCHED_NORMAL;而Linux支持两种类型的进程,实时进程和普通进程。实时进程可以采用SCHED_FIFO 和SCHED_RR调度策略;普通进程则采用SCHED_NORMAL调度策略。从…...
)
安装 RustDesk 服务器 (适用 Rocky Linux, CentOS, RHEL 系列发行版)
环境:Rocky Linux 9.1 1. 安装 Docker Engine 可以参考 [[linux-docker-rocky-install]] https://cc01cc.com/2023/03/02/linux-docker-rocky-install/英文可以参考官方文档 Install Docker Engine on RHEL https://docs.docker.com/engine/install/rhel/ 2. 安装…...

23种设计模式-策略模式
策略模式是一种设计模式,它允许在运行时选择算法的行为。它定义了算法家族,分别封装起来,让它们之间可以互相替换,此模式让算法的变化独立于使用算法的客户端。在本文中,我们将深入探讨策略模式的概念和实际应用&#…...

C#开发的OpenRA的游戏主界面怎么样创建
通过前面加载界面布局数据,可以把整个界面逻辑的数据加载到内存, 但是这些数据怎么显示出来,又是没有定义的。比如前面定义了多个界面的布局, 又是怎么样知道需要显示哪一个界面? 现在就来解决这个问题,其实整个游戏都是可以通过yaml文件进行配置的, 所以我们需要从yaml…...

考研还是工作?两战失败老道有话说
老道入职第一周自我介绍谈谈考研谈谈工作新的启程自我介绍 大家好!在下是一枚考研失败两次的自认为聪明能干的有点小帅的实则超级垃圾的三非名校毕业的自动化渣男。大一下就加入实验室,在实验室焊板子、画板子、培训、打比赛外加摸鱼;参加过…...

引用是否有地址的讨论的
说在前头,纯属个人理解,关于引用是否有地址,实际上并没有一个很统一的说法, C标准没有规定一个引用是否需要占用一块内存。 这里引用知乎“C 中引用是一块内存的标记,那引用本身有地址吗_百度知道 (baidu.com)”里面的…...
1、JAVA 开发环境搭建 - JDK 的安装配置
文章目录一、下载 JDK81、官网地址:[**https://www.oracle.com**](https://www.oracle.com)二、安装 JDK1、鼠标右键安装包,以管理员身份运行(无脑下一步即可)2、细节说明三、配置环境变量1、为啥要配置环境变量呢?2、原因分析3、配置环境变量…...

【Storm】【六】Storm 集成 Redis 详解
Storm 集成 Redis 详解 一、简介二、集成案例三、storm-redis 实现原理四、自定义RedisBolt实现词频统计一、简介 Storm-Redis 提供了 Storm 与 Redis 的集成支持,你只需要引入对应的依赖即可使用: <dependency><groupId>org.apache.storm…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...